Abstract
In this work, we present a structural investigation of sub-monolayer films of germanium on Ag(1 1 0) by means of photoelectron spectroscopy (XPS) and diffraction (XPD), as well as low-energy electron diffraction (LEED). Since the rising progress in the synthesis of various kinds of nanoribbons, also germanium nanoribbons (Ge-NR) have been synthesized on Ag(1 1 0), recently. Here, we focus on their structural evolution and found the formation of two different phases of germanium at coverages of \({0.5}\, \hbox {ML}\) and \({0.7}\,\hbox {ML}\), differing fundamentally from predicted nanoribbon structures. By means of LEED measurements, we obtained evidence for germanium superstructures which are not aligned along the \([{\overline{1}}\;1\;0]\)-direction, as expected for nanoribbon growth. Using synchrotron-based high-resolution XPS and XPD experiments of the Ge 3d and Ag 3d core-levels, we resolved the local chemical and atomic order of the germanium films. Thus, the strong internal bonding of the buckled germanium film and a weak Van-der-Waals interaction between silver and germanium were discovered. Moreover, XPD-simulations delivered a detailed model of the structural arrangement of the preliminary nanoribbon phase, which also provided an approach to identify the origin of the two chemically shifted components in the Ge 3d signal by applying a component-wise decomposition of the XPD data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Since the breakthrough of graphene in 2004, the novel field of two-dimensional materials in solid-state physics has expanded massively. Group IV-elements, like silicon and germanium, also exist synthetically in hexagonal honeycomb-structures, the so-called Xenes, as theoretically proposed in 1994 (Takeda and Shiraishi 1994). These 2D materials beyond graphene provide similar impressive electronic properties, like Dirac-characteristic band structure, and large thermal and electrical conductivities due to the electrons’ ultra-high Fermi velocity (Molle et al. 2017; Balendhran et al. 2015). In contrast to graphenes \(sp^2\)-hybridized carbon atoms causing a metallic electronic structure including a zero-bandgap (Rao et al. 2010), the single-element 2D-Xenes beyond carry out a transition to semiconducting electronics by a higher part of \(sp^3\)-hybridized atoms (Molle et al. 2017). It results from a large lattice constant of the group IV-Xenes compared to the graphene, causing a higher buckling of the honeycomb-lattice. Buckling is a key-parameter for the structure, which has a strong impact on the electronic structure of the materials, while the Dirac-characteristic is still retained (Molle et al. 2017; Cahangirov et al. 2009).
As opposed to the synthesis of graphene, silicene and Co. are not commonly stable in their freestanding form and must be grown on substrates (Gao et al. 2017; Vishnoi et al. 2019). However, according to the report of the first synthesis of silicene (Vogt et al. 2012), germanene (Dávila et al. 2014), and other group IV-Xenes (Yuhara and Lay 2020), several studies about electronical and structural properties have been published (Avila et al. 2013; Lin et al. 2018; Maniraj et al. 2019). In the case of germanene, it turned out that the structural and electronical properties are strongly depending on the carrier substrates (Gao et al. 2017; Molle et al. 2017). Moreover, high Z-materials, like germanene impress by their strong spin-orbit coupling, that might attain the use of spin-effects for applications in spintronics, like tunable spin-transport or quantum spin Hall effect (Wang et al. 2012; Liu et al. 2011). During the progressing research of 2D materials, low-dimensional formations in general received attention. Despite a lot of theoretical predictions of promising properties, only a few studies related to low-dimensional structures, like one-dimensional nanoribbons of silicon or germanium (Pang et al. 2011; Kosevich et al. 2013; Zhou et al. 2014; Matthes and Bechstedt 2014; Monshi et al. 2017). After the report on the first synthesis of silicon nanoribbons (Si-NR) on Ag(1 1 0) (Leandri et al. 2005), the experimental work on the analysis of germanium nanoribbons (Ge-NR) has also been initiated. Lately, Yuhara et al. reported about the first epitaxial growth of stable Ge-NR on Ag(1 1 0) via segregation. In contrast to the structural formation of Si-NR on Ag(1 1 0), which arrange in pentagons within the nanoribbon (Prévot et al. 2016), Ge-NR appear to align in parallel zigzag formations of hexagons along the \([{\overline{1}}\;1\;0]\)-direction (Yuhara et al. 2021).
During the evolution of Ge-NR, preliminary phases of germanium emerge at lower coverages, as has been reported in previous studies (Yuhara et al. 2021; Leandri et al. 2004). Here, we will present a detailed analysis of the interfacial and internal structure of these phases. To provide a detailed structure determination, we combine our findings on the long-range structure from LEED measurements with results of the chemical short-range order obtained by photoelectron spectroscopy (XPS) and diffraction (XPD). The comprehensive XPS and XPD measurements were performed with synchrotron radiation from the electron storage ring DELTA.
Experimental setup and methods
All preparation steps and measurements were conducted in situ in a UHV chamber with a base pressure below \(p < 1\times 10^{-10}\, \hbox {mbar}\). The analysis chamber is equipped with a hemispherical electron analyzer for XPS and XPD measurements, as well as a 4-grid LEED system, a sputter gun, and a sample heating stage. The sample is mounted on a 5-axis manipulator, which is movable in x-, y-, and z-direction and rotatable around the polar axis \(\varTheta\) and the azimuthal axis \(\phi\), with respect to the surface normal. The experimental setup is located at beamline 11 of the Center for Synchrotron radiation DELTA in Dortmund. This undulator beamline provides tunable soft x-ray radiation in an energy range of \({55}\, {\hbox {eV}}\le {h}\nu \le {1500}\, {\hbox {eV}}\) from a plane-grating monochromator for surface sensitive, angle-resolved XPS, and XPD (Westphal et al. 2005). The Ag(1 1 0) sample was prepared by several cycles of argon-ion sputtering at kinetic energies of \(E_{\mathrm {Ar}^+} = {700}\, {\hbox {eV}}\) and subsequent annealing at \(T = {720}\, \hbox {K}\). The cleanness and long-range order of the surface were checked by XPS survey spectra over large energy ranges and LEED measurements. To grow epitaxially thin films of germanium on the reconstructed Ag(1 1 0) surface, physical vapor deposition was used. An evaporation rate of \(\sim {11}\, {\AA }\hbox {h}^{-1}\) was chosen to keep the deposition time short, while keeping the sample at a temperature of about \(T = {500}\, \hbox {K}\) during evaporation. In the course of the preparation, two phases of germanium formations were found at different coverages. These phases were investigated by LEED and XPS. After recording the LEED patterns at various kinetic energies \(E_\mathrm {kin}\), each diffraction pattern was modeled by LEEDpat (Hermann and Van Hove 2014) to identify reconstructions, superstructures, and their corresponding real-space lattice.
High-resolution XPS spectra of the Ag 3d and Ge 3d core-levels were recorded at \({h}\nu = {440}\, {\hbox {eV}}\) and \({h}\nu = {140}\, {\hbox {eV}}\), respectively. Spectra recorded at normal emission provide bulk component information mainly, while emission angles at \(\varTheta = {60}^{\circ }\) are highly sensitive to the signals of the surface atoms. Thereby, possible surface effects of single components can be illustrated by comparing both spectra. Within the analysis, the spectra were normalized to the total peak maximum. Additionally, a Shirley background was removed from the Ag 3d spectra, as well as a Tougaard background from the Ge 3d data (Shirley 1972; Tougaard and Jørgensen 1985). For the peak fitting, components of a Voigt profile and a convolution of a Gaussian and Doniach–Sunjic function were applied to the signals of Ag 3d and Ge 3d, respectively (Armstrong 1967; Doniach and Sunjic 1970). The fit procedure was carried out with UNIFIT 2021 (Hesse and Denecke 2011).
Additionally, XPD measurements were performed to resolve the local atomic structure. For XPD, polar and azimuthal angles were varied in ranges of \({2}^{\circ }\le \varTheta \le {72}^{\circ }\) and \({0}^{\circ }\le \phi < {360}^{\circ }\), with step widths of \(\varDelta \varTheta = {2}^{\circ }\) and \(\varDelta \phi = {1.8}^{\circ }\), respectively. The finally presented XPD patterns show the intensity variation obtained from 7200 individual XPS spectra. The noticeable intensity modulation over the entire pattern is due to processes of elastic scattering of the emitted spherical photoelectron waves at neighboring atoms (Fadley 1984; Westphal 2003). Simulated XPD patterns for test structures were performed to receive structure information. The simulations applied the EDAC package, which is perfectly adapted for calculating diffraction pattern at kinetic energies of \(E_\mathrm {kin}>{50}\, {\hbox {eV}}\) (García de Abajo et al. 2001). The local atomic environment of emitting atoms can be determined by comparing simulated and experimental patterns, with the agreement measured by a reliability factor (R-factor) (Woodruff and Bradshaw 1994),
In Eq. (1), the anisotropy function \(\chi _i(\phi ,\,\varTheta )\) is defined as \(\chi _i(\phi ,\,\varTheta ) = \frac{I(\phi ,\varTheta )-\overline{I(\varTheta )}}{\overline{I(\varTheta )}}\), with \(I(\phi ,\varTheta )\) as measured intensity at angles \(\phi\) and \(\varTheta\), and \(\overline{I(\varTheta )}\) denotes the averaged intensity at polar angle \(\varTheta\). The R-factor analysis yields the values of \(0\le {R}\le 2\), with \({R}=0\) indicating a perfect agreement between measured and simulated patterns. \({R}=1\) and \({R} = 2\) correspond to no and a total anti-correlation between the patterns, respectively. A genetic algorithm was used to find the global best-matching structure to the experimental results (Döll and Van Hove 1996; Viana et al. 2007). It applies small structure variations, like a translation or scaling to a chosen start structure. However, a minimal R-factor can be found after a number of iteration steps, which corresponds to the best-matching structure.
Results and discussion
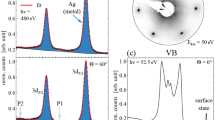
Survey spectra of the clean and Ge-covered Ag(1 1 0)-surface corresponding to the chemical composition of the sample systems. The spectra were taken at a photon energy of \({h}\nu = {700}\, {\hbox {eV}}\), and at an emission angle of \(\varTheta = {60}^{\circ }\) for enhanced surface sensitivity. The binding energy of the spectra was referenced to the Fermi edge
To expand the first studies on low-dimensional germanium formation on Ag(1 1 0) (Leandri et al. 2004), as well as to complete the structural evolution up to the growth of Ge-NR (Yuhara et al. 2021), we present a detailed structural analysis of the preliminary phases of Ge-NR. After a thorough preparation of the Ag(1 1 0) substrate sample, the cleanness and reconstructed order of the surface were checked by XPS and LEED, respectively. XPS survey spectra were recorded at a photon energy of \({h}\nu = {700}\, {\hbox {eV}}\). These were taken at an emission angle of \(\varTheta = {60}^{\circ }\) to enhance the surface sensitivity. In Fig. 1 the cyan plotted curve displays a spectrum of the clean Ag(1 1 0) surface indicating no residues of contamination by carbon or oxygen, as marked by the red boxes at the corresponding energies of the C 1s and O 1s signals. Furthermore, the typical photoelectron and Auger features of pure silver are highlighted in Fig. 1. The dominant peaks of the Ag 3d core-level will be discussed in detail later.
Figure 2a displays a LEED pattern of the clean Ag(1 1 0) surface, taken at a kinetic energy of \(E_\mathrm {kin} = {65}\, {\hbox {eV}}\). The sharp diffraction spots of the \((1\times 1)\) unit cell indicate an excellent surface periodicity. The length ratio of the silver surface base vectors \(\mathbf {a}_1\) and \(\mathbf {a}_2\) satisfies the ratio of \(\mathbf {a}_1/\mathbf {a}_2=1/\sqrt{2}\). After deposition of \({0.5}\,\hbox {ML}\) and \({0.7}\,\hbox {ML}\) a significant change in periodicity and in electronic structure of the sample system was observed, which will be discussed in the following sections. The definition of a monolayer refers to the first study on this system (Leandri et al. 2004), corresponding to a total coverage of the surface. In Fig. 1, the magenta and yellow plotted spectra were recorded for the \({0.5}\, \hbox {ML}\) and \({0.7}\, \hbox {ML}\) coverage of Ge on Ag(1 1 0), respectively. The emerging signals of germanium, such as Ge 3s, Ge 3p, and Ge 3d, of different amounts for both layer thicknesses demonstrate a successful preparation of germanium films on Ag(1 1 0). The absence of carbon and oxygen signals proves the systems purity.
LEED
As a result of the epitaxial growth of \({0.5}\, \hbox {ML}\) germanium on the clean substrates surface, the LEED pattern shown in Fig. 2a turns into (b).
LEED patterns, measured at \(E_\mathrm {kin} = {65}\, {\hbox {eV}}\), of (a) the clean Ag(1 1 0) surface and (b) after deposition of \({0.5}\,\hbox {ML}\) germanium. A \(c(4\times 2)\)-superstructure is indicated by sharp LEED spots. A simulation of the experimental pattern is given in (c) k-space illustration and in (d) real space. The unit cells’ base vectors \(\mathbf {a}_1\), \(\mathbf {a}_2\), \(\mathbf {b}_1\), and \(\mathbf {b}_2\) are marked by red and blue arrows for the substrate and the adsorbate, respectively
A \(c(4\times 2)\)-superstructure is formed, which is expressed by \(\left( {\begin{matrix}1 &{} 1\\ -2 &{} 2 \end{matrix}}\right)\) in matrix notation. A simulation of the systems lattice structure was performed using LEEDpat (Hermann and Van Hove 2014) and is given in Fig. 2c, d as illustration of the reciprocal and real lattice, respectively. The red and blue arrows represent the substrate and adsorbate unit cell vectors. Assuming a lattice constant of \(a_0 = {4.09}\, {{\AA }}\) for the silver substrate (Ashcroft and Mermin 1976) leads to a size of \(({11.56}\times {8.18})\,{\AA }^{2}\) for the unit cell of the centered germanium superstructure at a coverage of \({0.5}\, \hbox {ML}\). A centered superstructure indicates a rotated adsorbate structure with respect to the unit cell vectors of the substrate. The real-space visualization of the \(c(4\times 2)\)-structure, as displayed in Fig. 2d, exemplifies the rotation of the germanium formation of around \({35}^{\circ }\) regarding the \([{\overline{1}}\;1\;0]\)-direction of the substrate. In contrast to this observation, the Si- and Ge-NR growth strictly follows the \([{\overline{1}}\;1\;0]\)-direction (Prévot et al. 2016; Yuhara et al. 2021), which seems to be energetically unfavorable for the germanium formation at low coverages.
LEED patterns, taken at electrons’ kinetic energy of \(E_\mathrm {kin} = {65}\, {\hbox {eV}}\), a after growing \({0.6}\, {ML}\) and b \({0.7}\, \hbox {ML}\) of germanium on the Ag(1 1 0) surface. A corresponding simulation of the pattern, presented in c k-space and d real space, reveals the formation of two domains with larger unit cell
Going one step further in the structural evolution of Ge/Ag(1 1 0) the LEED pattern, as shown in Fig. 3, is observed. After deposition of \({0.6}\, \hbox {ML}\), the \(c(4\times 2)\) spots of the germanium supercell are split, while the \((1\times 1)\) substrate spots remain without modifications. This observation is clearly displayed in the LEED pattern of Fig. 3a, which is obtained at an electrons’ kinetic energy of \(E_\mathrm {kin} = {65}\, {\hbox {eV}}\). At coverages of \({0.7}\, \hbox {ML}\), the LEED pattern of Fig. 3b was obtained. Now, the LEED spots of the Ge-supercell are more split when compared to the pattern of the slightly lower coverage of Fig. 3a. The apparent splitting can be described by reflexes originating from two domains. The unit cells of these domains are larger than the unit cell of the substrate as displayed in the simulated diffraction patterns in Fig. 3c, d. The domains are described by matrices \(\left( {\begin{matrix} 2&{}1\\ -3&{}2 \end{matrix}}\right)\) and \(\left( {\begin{matrix} 2&{}1\\ -3&{}-2 \end{matrix}}\right)\), with the real space lattice of the first domain depicted in Fig. 3d. Compared to the \(c(4\times 2)\)-superstructure of Fig. 2a, the unit vector \(\mathbf {b}_2\) of the supercell in Fig. 3b is extended by \({60}{\%}\).
XPS
Figure 4a shows the high-resolution spectra of the Ag 3d orbital of the clean Ag(1 1 0) surface. After removing the Shirley background, a Voigt profile without asymmetry was applied to the single-component shaped peak (Hüfner and Wertheim 1975). The Ag 3d peak is split into its 3d\(_{3/2}\)- and 3d\(_{5/2}\)-component by \(E_\mathrm {SOC} = {6.0}\, {\hbox {eV}}\) due to spin-orbit coupling. All fit parameters of the peaks are listed in Table 1, with individual deviations caused by rounding errors. The appearance of energy loss features P1, P2, and P3 caused by surface plasmons indicates a well-prepared surface, which became obvious in the spectrum taken at \(\varTheta ={60}^{\circ }\) (Leiro et al. 1983).
High-resolution XPS spectra of the symmetric Ag 3d core-level signal measured at a photon energy of \({h}\nu = {440}\, {\hbox {eV}}\) and at detection angles of \(\varTheta ={0}^{\circ }\) (top) and \(\varTheta ={60}^{\circ }\) (bottom). a Corresponds to the clean Ag sample, while b, c reflect the signals of the silver interface below \({0.5}\, \hbox {ML}\) and \({0.7}\, \hbox {ML}\) of germanium, respectively. Table 1 displays the corresponding fit parameters
Figures 4b, c display the photoelectron spectra of sub-monolayer Ge-films on Ag(1 1 0). Obviously, the surface plasmon signals disappeared, which was also reported in the previous studies for Si-NR growth on Ag(1 1 0) (Espeter et al. 2017). Apart from this, no significant modifications in the Ag 3d peak can be noted in the spectra of Fig. 4b, c. Therefore, it can be assumed that no strong chemical bond between Ag and Ge is formed due to a missing chemical shifted Ag–Ge interface component in the Ag 3d signal after Ge deposition. It is more likely that germanium is interacting weakly with the silver substrate by Van-der-Waals forces.
Figure 5 displays high-resolution XPS spectra of the Ge 3d core-level for different layer thicknesses, recorded at a photon energy of \({h}\nu = {140}\, {\hbox {eV}}\). The Ge 3d core-level signals appear in an asymmetric peak shape with a tailing to lower kinetic energies. This indication of the metallic character of the adsorbate formation has already been observed for both sub-monolayer Ge-films and Ge-NR on silver substrates (Oughaddou et al. 2000a, b; Yuhara et al. 2021). Therefore, the data were fitted applying a convolution of a Gaussian and a Doniach–Sunjic distribution with asymmetry parameter \(\alpha\). Both signals are spin-orbit split by \(E_\mathrm {SOC} = {0.56}\, {\hbox {eV}}\), and each is composed of two chemically shifted components. The ratio of the relative areas is approximately \(\mathrm {Ge\;1}/\mathrm {Ge\;2}=3\) at \(\varTheta ={0}^{\circ }\) and \(\mathrm {Ge\;1}/\mathrm {Ge\;2}={3.5}\) at \(\varTheta ={60}^{\circ }\). At a coverage of \({0.5}\, \hbox {ML}\), the analysis of the germanium signal, shown in Fig. 5(a), yields a chemical shift of \(\varDelta E_\mathrm {chem}={0.19}\, {\hbox {eV}}\) between the Ge 1 and Ge 2 components, originating from their different chemical environments. Both components Ge 1 and Ge 2 are assigned to the internal structure of the germanium film. An asymmetry of \(\alpha = {0.11}\) was found, which had also been reported for Si- and Ge-NR on Ag(1 1 0) (Espeter et al. 2017; Yuhara et al. 2021).
High-resolution XPS spectra of the Ge 3d signal for Ge coverages of a \({0.5}\, \hbox {ML}\) and b \({0.7}\, \hbox {ML}\). The spectra were recorded at a photon energy of \({h}\nu = {140}\, {\hbox {eV}}\), under emission angles of \(\varTheta ={0}^{\circ }\) (top) and \(\varTheta ={60}^{\circ }\) (bottom). Both signals are revealing two components Ge 1 and Ge 2 which are chemically shifted by a \(E_\mathrm {SOC}={0.19}\, {\hbox {eV}}\) and b \(E_\mathrm {SOC}={0.16}\, {\hbox {eV}}\), respectively. Table 2 displays the corresponding parameters of the fit
According to the high surface sensitivity of the performed XPS measurements, slight surface effects of both components can be noted from a comparison of the relative area ratio at different emission angles. When the polar angle is varied from \(\varTheta ={0}^{\circ }\) to \(\varTheta ={60}^{\circ }\), the intensity of component Ge 1 increases slightly by 5%, while the intensity of component Ge 2 is significantly reduced by 14%. In addition to the mean area ratio of \(\mathrm {Ge\,1}/\mathrm {Ge\,2}=3\), we suppose a buckled structure, with a quarter of the germanium atoms, effecting component Ge 2, is closer to the interface than the group of atoms to component Ge 1. However, when comparing the \({0.5}\, \hbox {ML}\) and \({0.7}\, \hbox {ML}\) spectra, the Ge 3d high-resolution XPS spectra appear being fairly similar, as displayed in Fig. 5a, b. The rather small differences in the spectra suggest only minor modifications of the structure. For both coverages, the number of components is the same, while the chemical shift is reduced to \({0.16}\, {\hbox {eV}}\) and the components’ full width half maximum (FWHM) is broadened by 21% for the \({0.7}\, \hbox {ML}\) film. These results are in excellent agreement with our findings from the LEED measurements assuming an enlarged Ge-supercell size. The area shares in the XPS spectra for the components Ge 1 and Ge 2 differ obviously from the ratio obtained for the \({0.5}\, \hbox {ML}\) structure. Thus, the additional germanium atoms preferably arrange in the top-most Ge 1 environment as concluded from the raised Ge 1/Ge 2-ratio observed for the \({0.7}\, \hbox {ML}\) phase. This is concluded from the experimental data, since the Ge 1-signal increases by 12% for a polar angle variation from \(\varTheta ={0}^{\circ }\) to \(\varTheta ={60}^{\circ }\). Component Ge 2 is allocated at the Ag-interface, which is indicated by its clear intensity decrease of 39% at the higher emission angle.
XPD
Following the chemical analysis of the sample systems, we come to the structural investigation with the use of XPD measurements. In this section, we will focus the structure determination of the \({0.5}\, \hbox {ML}\) phase, which will be discussed in the following. However, for experimental and resources reasons, XPD measurements of the \({0.7}\, \hbox {ML}\) phase were not carried out. Therefore, XPD pattern of the Ge 3d core level were recorded at a photon energy of \({h}\nu = {140}\, {\hbox {eV}}\). In Fig. 6a, a Ge 3d diffraction pattern is presented which was recorded at a kinetic energy of \(E_\mathrm {kin} = {107.5}\, {\hbox {eV}}\). It reveals a twofold rotational symmetry and a mirror plane. For reducing experimental artifacts in the pattern, these symmetry operations as well as a minor Gaussian blur were applied.
a Experimental XPD pattern of Ge 3d photoelectrons recorded at a kinetic energy of \(E_\mathrm {kin} = {107.5}\, {\hbox {eV}}\). For excitation, a photon energy of \({h}\nu = {140}\, {\hbox {eV}}\) was used. b The simulated XPD pattern was obtained for the best-matching structure, as shown in Fig. 7. It was found by modifying test structures within a genetic algorithm. The agreement between a and b is evaluated by an R-factor of \({R}={0.07}\)
Within the XPD simulation, a first test structure was chosen, which is based on the model proposed by Leandri et al. (2004). In that structure model, a supercell was selected, which contained 8 equidistant Ge-atoms, and which matched the \(c(4\times 2)\)-structure obtained by LEED.
The calculation of the pattern by means of EDAC was conducted over the full experimental angular range of \({70}^{\circ }\), using a scatter radius of \({8.5}\, {\AA }\) for all eight emitters, which is determined by the inelastic mean free path (IMFP) at the electrons kinetic energy (García de Abajo et al. 2001; Shinotsuka et al. 2015). This test structure model resulted in an R-factor of \({R}={0.75}\), which indicated a rather poor match. Subsequently, the genetic algorithm was applied to find a structure model with improved consistency between experimental and simulated patterns. The algorithm applies small variations to test structures, like translations of \(\pm \,{0.3}\, {\AA }\) in x-, y-, and z-directions, as well as a scaling of the cluster by \(\pm \,{0.5}{\%}\). The best-matching pattern is displayed in Fig. 6b impressing by a high agreement with an R-factor of \({R}={0.07}\). The corresponding structure is presented in Fig. 7. The Ge- and Ag-atoms are visualized by green and silver spheres, respectively.
Determination of a structural model for \({0.5}\, \hbox {ML}\) Ge on the Ag(1 1 0) surface. It results from a comparison of the experimental against the simulated pattern, where the structure model was modified within the simulation by applying a genetic algorithm. The unit cells of germanium (blue) and silver (red dashed) are marked in a top view and b side view. The strongly buckled germanium formation satisfies the \(c(4\times 2)\)-superstructure, with two different chemical environments of Ge 1 and Ge 2 highlighted in light and dark green, respectively
The \(c(4\times 2)\) Ge-supercell is illustrated in blue, while the unit cell of the Ag(1 1 0) substrate is plotted in red. In this model, we found unit cell sizes of \(({2.9}\times {4.1})\,{\AA }^{2}\) and \(({11.5}\times {8.2})\,{\AA }^{2}\) for Ag and Ge, respectively. These values are in outstanding agreement with the theoretical and experimental reported values (Ashcroft and Mermin 1976; Yuhara et al. 2021). From the simulations, a tendency of forming islands of tetramers rather than equidistant atom positions is obtained, as depicted in Fig. 7a. This can even be observed in the STM measurements of this system, that have recently been published (Yuhara et al. 2021). The internal structure of the tetramer groups revealed slightly different bonding lengths of the inner germanium bonds, leading to two different chemical environments as observed, which are illustrated in Fig. 7 by different color shades. The ratio of the atoms in different chemical environments in the structure model is \(\mathrm {Ge\,1}/\mathrm {Ge\,2}=3\). The model perfectly satisfies the area ratio obtained from the corresponding XPS spectra in Fig. 5a. In Fig. 7b, the side view of the structure found within the XPD analysis confirms the previous assumptions based on XPS of the formation of a buckled germanium structure with weak interaction to the substrate. At the interface a clear separation of Ge and Ag without layer intermixing was found. This was supported by XPS, as shown before, due to the absence of any Ag–Ge component in both core-level spectra. The strong buckling as supported by the XPS results and discussed in Sect. 3.2 is also mirrored within the structure model here. A maximum buckling of \(\delta _\mathrm {max}={0.9}\, {\AA }\) for the Ge-structure was determined, with the Ge 2-atoms being located directly at the Ag-interface and the Ge 1-atoms forming the top-most part of the layer.
The combined high-resolution XPS and XPD analysis allows a structural investigation with high chemical sensitivity. A total of 7200 XPS spectra resulting in a XPD pattern were fitted as presented in the XPS analysis of Fig. 5a and in Fig. 8. This enables to decompose the complete XPD data set into separate diffraction pattern for the chemically shifted components Ge 1 and Ge 2. The yielded experimental XPD patterns of the decomposition are shown in Fig. 8a, c, corresponding to the chemical environments Ge 1 and Ge 2, respectively.
Component decomposed XPD patterns of \({0.5}\, \hbox {ML}\) Ge on Ag(1 1 0). The patterns a and c, corresponding to XPS components Ge 2 and Ge 1 in b, were obtained from the experimental pattern of Fig. 6a. The diffraction features represent the local environments as marked in e. Simulations of the respective emitters provide diffraction patterns in d and f for Ge 2 and Ge 1, respectively. The agreement to the experimental pattern is expressed by the low R-factors. Both patterns d and f were simulated for the same structure model e
Figure 8e shows the unit cell of the here proposed structure. The different chemical environments correspond to components Ge 1 and Ge 2 and are marked in dark and light green, respectively. The simulation of the different local environments led to the two XPD patterns given in Figs. 8d, f. For obtaining these simulated patterns, all parameters of the entire unit cell were kept identical and again small variations of \(\pm \,{0.1}\, {\AA }\) were applied to the atomic cluster. The agreement between experiment and simulation yielded R-factors of \({R}={0.05}\) for the dominant component Ge 1 and \({R}={0.17}\) for the minor due of component Ge 2, which indicated an excellent agreement to the previously conducted LEED and XPS analysis. Within the decomposition method, especially the buckling of the \({0.5}\, \hbox {ML}\) structure was confirmed by the fact that both components reflect the respective chemical environment.
Conclusion
In this work, we presented the missing piece of the structural evolution of Ge-NR on Ag(1 1 0). Therefore, two preliminary phases of Ge-NR at coverages of \({0.5}\, \hbox {ML}\) and \({0.7}\, \hbox {ML}\) were investigated by means of LEED, XPS, and XPD. First, a \({0.5}\, \hbox {ML}\) phase of germanium was prepared on a clean Ag(1 1 0) surface, forming a \(c(4\times 2)\)-superstructure. The high-resolution XPS spectra of Ag 3d and Ge 3d core-levels showed only weak interface bonding. In the internal structure of the germanium film, two different chemical environments were identified. By analyzing these environments, a strongly buckled phase was supposed by XPS and confirmed by XPD measurements. The \(c(4\times 2)\)-structure consists of two tetramer groups with a strongly buckled and non-equidistant internal structure. The Ge-film is Van-der-Waals bonded to the Ag-substrate. A detailed structural model of the internal and interfacial structure was presented.
When increasing the germanium coverage to \({0.7}\, \hbox {ML}\), new LEED spots appeared. A quantitative LEED pattern analysis yielded two domains at the surface, which are characterized by \(\left( {\begin{matrix} 2&{}1\\ -3&{}2 \end{matrix}}\right)\) and \(\left( {\begin{matrix} 2&{}1\\ -3&{}-2 \end{matrix}}\right)\). For this phase, strong internal bonds and a rather weak interaction at the interface were identified by XPS.
The provided structure model, as well as the structural discussion of the intermediate phases toward the Ge-NR growth will help to understand the structural evolution of low-dimensional germanium nanocomposites.
References
Armstrong B (1967) Spectrum line profiles: the Voigt function. J Quant Spectrosc Radiat Transfer 7:61
Ashcroft NW, Mermin ND (1976) Solid state physics, vol 2005. Holt, Rinehart and Winston, New York
Avila J, Padova PD, Cho S, Colambo I, Lorcy S, Quaresima C, Vogt P, Resta A, Lay GL, Asensio MC (2013) Presence of gapped silicene-derived band in the prototypical (3 × 3) silicene phase on silver (111) surfaces. J Phys Condens Matter 25:262001
Balendhran S, Walia S, Nili H, Sriram S, Bhaskaran M (2015) Elemental analogues of graphene: silicene, germanene, stanene, and phosphorene. Small 11:640
Cahangirov S, Topsakal M, Aktürk E, Şahin H, Ciraci S (2009) Two- and one-dimensional honeycomb structures of silicon and germanium. Phys Rev Lett 102:236804
Dávila ME, Xian L, Cahangirov S, Rubio A, Lay GL (2014) Germanene: a novel two-dimensional germanium allotrope akin to graphene and silicene. New J Phys 16:095002
Döll R, Van Hove M (1996) Global optimization in LEED structure determination using genetic algorithms. Surf Sci 355:L393
Doniach S, Sunjic M (1970) Many-electron singularity in X-ray photoemission and X-ray line spectra from metals. J Phys C Solid State Phys 3:285
Espeter P, Keutner C, Roese P, Shamout K, Berges U, Wenzel G, Bignardi L, Kleimeier NF, Zacharias H, Westphal C (2017) Facing the interaction of adsorbed silicon nano-ribbons on silver. Nanotechnology 28:455701
Fadley CS (1984) Angle-resolved X-ray photoelectron spectroscopy. Prog Surf Sci 16:275
Gao N, Liu H, Zhou S, Bai Y, Zhao J (2017) Interaction between post-graphene group-IV honeycomb monolayers and metal substrates: implication for synthesis and structure control. J Phys Chem C 121:5123
García de Abajo FJ, Van Hove MA, Fadley CS (2001) Multiple scattering of electrons in solids and molecules: a cluster-model approach. Phys Rev B 63:075404
Hermann KE, Van Hove MA (2014) LEEDpat, Version 4.2. Fritz-Haber-Institut / Hong Kong Baptist University, Berlin / Hong Kong (2014). http://www.fhi-berlin.mpg.de/KHsoftware/LEEDpat/index.html
Hesse R, Denecke R (2011) Improved Tougaard background calculation by introduction of fittable parameters for the inelastic electron scattering cross-section in the peak fit of photoelectron spectra with UNIFIT 2011. Surf Interface Anal 43:1514
Hüfner S, Wertheim GK (1975) Core-line asymmetries in the x-ray-photoemission spectra of metals. Phys Rev B 11:678
Kosevich YA, Savin AV, Cantarero A (2013) Effects of quantum statistics of phonons on the thermal conductivity of silicon and germanium nanoribbons. Nanoscale Res Lett 8:7
Leandri C, Oughaddou H, Gay J, Aufray B, Le Lay G, Bibérian J, Ranguis A, Bunk O, Johnson R (2004) Self-assembled germanium nano-clusters on silver(110). Surf Sci 573:L369
Leandri C, Lay GL, Aufray B, Girardeaux C, Avila J, Dávila M, Asensio M, Ottaviani C, Cricenti A (2005) Self-aligned silicon quantum wires on Ag(110). Surf Sci 574:L9
Leiro J, Minni E, Suoninen E (1983) Study of plasmon structure in XPS spectra of silver and gold. J Phys F Met Phys 13:215
Lin CH, Huang A, Pai WW, Chen WC, Chen TY, Chang TR, Yukawa R, Cheng CM, Mou CY, Matsuda I, Chiang TC, Jeng HT, Tang SJ (2018) Single-layer dual germanene phases on Ag(111). Phys Rev Mater 2:024003
Liu CC, Feng W, Yao Y (2011) Quantum Spin hall effect in silicene and two-dimensional germanium. Phys Rev Lett 107:076802
Maniraj M, Stadtmüller B, Jungkenn D, Düvel M, Emmerich S, Shi W, Stöckl J, Lyu L, Kollamana J, Wei Z, Jurenkow A, Jakobs S, Yan B, Steil S, Cinchetti M, Mathias S, Aeschlimann M (2019) A case study for the formation of stanene on a metal surface. Commun Phys 2:12
Matthes L, Bechstedt F (2014) Influence of edge and field effects on topological states of germanene nanoribbons from self-consistent calculations. Phys Rev B 90:165431
Molle A, Goldberger J, Houssa M, Xu Y, Zhang SC, Akinwande D (2017) Buckled two-dimensional Xene sheets. Nat Mater 16:163
Monshi M, Aghaei S, Calizo I (2017) Edge functionalized germanene nanoribbons: impact on electronic and magnetic properties. RSC Adv 7:18900
Oughaddou H, Aufray B, Le Lay G, Gay J, Zeysing J, Johnson R, Barrett N, Guillot C (2000b) Semiconductor on metal adsorption: Ge tetramers on the Ag(001) surface. Appl Surf Sci 162–163:74
Oughaddou H, Sawaya S, Goniakowski J, Aufray B, Le Lay G, Gay JM, Tréglia G, Bibérian JP, Barrett N, Guillot C, Mayne A, Dujardin G (2000a) Ge/Ag(111) semiconductor-on-metal growth: formation of an Ag2Ge surface alloy. Phys Rev B 62:16653
Pang Q, Zhang Y, Zhang JM, Ji V, Xu KW (2011) Electronic and magnetic properties of perfect and defected germanium nanoribbons. Mater Chem Phys 130:140
Prévot G, Hogan C, Leoni T, Bernard R, Moyen E, Masson L (2016) Si nanoribbons on Ag(110) studied by grazing-incidence X-ray diffraction, scanning tunneling microscopy, and density-functional theory: evidence of a pentamer chain structure. Phys Rev Lett 117:276102
Rao CNR, Sood AK, Voggu R, Subrahmanyam KS (2010) Some novel attributes of graphene. J Phys Chem Lett 1:572
Shinotsuka H, Tanuma S, Powell CJ, Penn DR (2015) Calculations of electron inelastic mean free paths. X. Data for 41 elemental solids over the 50 eV to 200 keV range with the relativistic full Penn algorithm. Surf Interface Anal 47:871
Shirley DA (1972) High-resolution X-ray photoemission spectrum of the valence bands of gold. Phys Rev B 5:4709
Takeda K, Shiraishi K (1994) Theoretical possibility of stage corrugation in Si and Ge analogs of graphite. Phys Rev B 50:14916
Tougaard S, Jørgensen B (1985) Absolute background determination in XPS. Surf Interface Anal 7:17
Viana ML, Muiño RD, Soares EA, Hove MAV, de Carvalho VE (2007) Global search in photoelectron diffraction structure determination using genetic algorithms. J Phys Condens Matter 19:446002
Vishnoi P, Pramoda K, Rao CNR (2019) 2D elemental nanomaterials beyond graphene. ChemNanoMat 5:1062
Vogt P, De Padova P, Quaresima C, Avila J, Frantzeskakis E, Asensio MC, Resta A, Ealet B, Le Lay G (2012) Silicene: compelling experimental evidence for graphene like two-dimensional silicon. Phys Rev Lett 108:155501
Wang Y, Zheng J, Ni Z, Fei R, Liu Q, Quhe R, Xu C, Zhou J, Gao Z, Lu J (2012) Half-metallic silicene and germanene nanoribbons: towards high-performance spintronics device. NANO 7:1250037
Westphal C (2003) The study of the local atomic structure by means of X-ray photoelectron diffraction. Surf Sci Rep 50:1
Westphal C, Berges U, Dreiner S, Follath R, Krause M, Schäfers F, Schirmer D, Schürmann M (2005) The plane-grating monochromator beamline at the U55 undulator for surface and interface studies at DELTA. J Electron Spectrosc Relat Phenom 144–147:1117
Woodruff DP, Bradshaw AM (1994) Adsorbate structure determination on surfaces using photoelectron diffraction. Rep Prog Phys 57:1029
Yuhara J, Lay GL (2020) Beyond silicene: synthesis of germanene, stanene and plumbene. Jpn J Appl Phys 59:SN0801
Yuhara J, Shimazu H, Kobayashi M, Ohta A, Miyazaki S, Takakura S, Nakatake M, Le Lay G (2021) Epitaxial growth of massively parallel germanium nanoribbons by segregation through Ag(110) thin films on Ge(110). Appl Surf Sci 550:149236
Zhou Y, Li X, Wang Z, Li S, Zu X (2014) Modulating the band gap of germanane nanoribbons for quantum well devices. Phys Chem Chem Phys 16:18029
Acknowledgements
The authors acknowledge the continuous support of the DELTA staff during and outside the beamtimes. We are grateful for financial support by the German federal state, the Land Nordrhein-Westfalen.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kesper, L., Schmitz, M., Schulte, M.G.H. et al. Revealing the nano-structures of low-dimensional germanium on Ag(1 1 0) using XPS and XPD. Appl Nanosci 12, 2151–2160 (2022). https://doi.org/10.1007/s13204-022-02478-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13204-022-02478-7