Introduction

Despite its tremendous potential, quantum-dot cellular automata (QCA) has failed to substitute the CMOS technology in the design of digital circuits and systems Lombardi et al. (2007). One major reason behind this predicament is the lack of electronic design and automation (EDA) support that could lead to a standard optimized implementation of the Boolean expressions Kalogeiton et al. (2017). On the contrary, EDA tools for the CMOS technology are likely to generate an identical (optimized) circuit for apparently different behavioral descriptions of the same entity in a hardware description language (HDL).

Arithmetic and logic unit (ALU) is an essential combinational circuit in any microprocessor, responsible for performing all arithmetic and logic operations. Usually an n-bit QCA–ALU, which is not yet optimized, will employ an array of n logic gates for each operation it is supposed to perform, plus a dedicated circuit for arithmetic operations. Just like any other combinational circuit, ALU is not restricted by a notion of time—it operates whenever it sees a change in one or more inputs. Naturally, all the arrays process this change in the input simultaneously irrespective of the desired operation. The control unit is then responsible to choose the correct result using a multiplexer (mux). This entire process leads to high power dissipation, and demands that the number of gates be reduced, and arrays for the unused gates must be kept silent to minimize this power overhead. One obvious way around this challenge (other than power gating) is to first synthesize the ALU (or any circuit for that matter) for CMOS, resulting in much smaller number of gates than the manually designed QCA–ALU, and then generate a register-transfer-logic (RTL) schematic. Once the designer is certain about the number and interconnection of the logic gates, an equivalent QCA implementation may follow. This approach was adopted by Niemier et al. Niemier and Kogge (2001) to implement an optimized ALU.

Besides being tedious, the above mentioned approach still has a loophole: while translating the standard RTL to QCA implementation, two designers are likely to yield different QCA layouts. Historically, we have seen multiple implementations even for elementary gates such as inverters and exclusive-OR (XOR) Beigh et al. (2013), let alone a complete system design. Even a small difference in the two layouts will yield substantial difference in performance, area, and power measures. It is, therefore, essential to somehow standardize the implementation of QCA-based digital circuits until their EDA support becomes sufficiently mature. The objective of this work is to propose a QCA-based standard logic cell that may be reconfigured to perform one of the seven most commonly used logic operations. Instead of having seven arrays (one for each logic operation) for an n-bit QCA–ALU, this approach will merely require one, which should be reconfigured by the control unit according to the instruction being executed.

Artificial neural networks (ANN) are known to have a tendency to learn, and minimize the difference between targets and the computed outputs in a least square sense Naqvi et al. (2016). They comprise a number of processing units called neurons, where each neuron carries a certain real weight Kamran et al. (2016). Provided with a different set of weights, each neuron is capable of performing a unique arithmetic/logic operation Haider et al. (2017)—enabling them to be an effective way of achieving real-time reconfigurability in digital circuits. What we propose to do in this work, therefore, is as follows:

  1. 1.

    Train the ANN in offline to pre-compute the weights for each logic operation.

  2. 2.

    Manually devise a Boolean expression for the ANN-based model, which when supplied with the pre-computed weights, produces output for a different logic operation—we call this expression the logic cell.

  3. 3.

    Obtain the QCA implementation for the logic cell, and thoroughly simulate it to verify each operation.

  4. 4.

    Cross validate the functionality of the logic cell by implementing the design for CMOS on an FPGA board from Xilinx.

Our FPGA synthesis suggests that our approach based on ANN yields the same RTL as any other behavioral description for the ALU—not incurring any additional overhead. Now any QCA–ALU built using this cell should always generate a standard optimized implementation. The rest of the paper is organized as follows: Sect. 2 presents a background of QCA and ANN, and reviews a few related works. The proposed design methodology is covered in Sect. 3. In Sect. 4 we present our simulation results and comparison with the state-of-the-art, before we conclude the paper in Sect. 5.

Background and related work

Overview of QCA

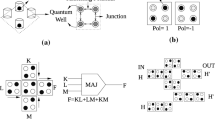
QCA is an emerging transistor-less technology, in which logic states are not stored as voltage levels, but as the position of individual electrons in the available quantum dots in each QCA cell Jayalakshmi and Amutha (2016). In case of binary QCA, there are two electrons that may tunnel between four available quantum-dots in each cell, whereas, in ternary QCA, the two electrons have eight dots available for tunneling in each cell Tehrani et al. (2014). An isolated QCA cell exhibits no polarization state, whereas, in presence of neighboring cells it possesses one of its stable states depending on the polarization state of its neighbor cells. Polarization P measures the level to which charge distribution is bringing into line along one of the diagonal axes. Let the charge density on the quantum dot be \(p_i\), then polarization is defined as in Eq. 1 (Singh et al. (2016)):

$$\begin{aligned} P = \frac{(p_1 + p_3) - (p_2 + p_4)}{p_1 + p_2 + p_3 + p_4} \end{aligned}$$
(1)

Electrons tunnel between these dots but can never leave the cell vacant; this concept is named as tunneling Yamahata et al. (2008). The electrons repel each other in the quantum cell because of their columbic interactions—resulting in two polarization states: \(P = 1\) and \(P = -1\). While the former is used as logic 1 or high/ON, the latter is used as logic 0. So the logic 0 and 1 are encoded in terms of polarization—1 and 1, respectively. The physical interaction between QCA cells makes implementation of algebraic expressions realistic. The propagation of binary information is done through an array of QCA cells that acts as a binary wire. The flow of information in QCA is controlled by a clock, which provides synchronization too Anderson et al. (2014). This clocking mechanism not only provides a controlled flow of information, but powers the QCA cells too—there is no other external power source Berggren et al. (2006). Whenever there is a loss of signal energy, it can be easily restored by the clock. The clock used in QCA is partitioned into four zones, where each zone has a phase difference of 90\(^{\circ }\). These zones can be of irregular shape, but their size must be within certain limits imposed by the fabrication and dissipation concerns. This clocking scheme has four clock phases namely: switch, hold, release, and relax. Refer to Beigh et al. (2013) for details.

Unlike CMOS, QCA has two basic gates: majority gate/voter (MV) and inverter (\(\lnot\)), shown in Fig. 1 Momenzadeh et al. (2005). The former implements the Boolean function \(F (A,B,C) = AB + AC + BC\). Each of these two gates can be implemented using just a single clock zone, and they lay the foundation of larger systems built by QCA. Note the two possible implementations of the inverter—each having its merits and demerits; discussing them, however, is beyond the scope of this work. This, however, further strengthens our motivation to propose a standard implementation, since each inverter should lead to vastly different larger circuits. Table 1 summarizes the other commonly used logic gates built using the basic QCA gates, along with their equivalent QCA implementations.

Fig. 1
figure 1

Elementary logic gates in QCA: a majority gate, b inverter 1, c inverter 2

Full size image
Table 1 Various logic gates implemented using majority and inverter gates
Full size table

Overview of ANN

ANN are described as a cascaded interconnection of neurons Gl et al. (2015), which provides mapping from inputs to outputs via a few hidden layers—each layer may carry multiple neurons. The objective of such a network is to minimize the difference between the expected and target responses for a given set of inputs by means of iterative learning. The response of the network is given by Eq. 2, where \(P_R\) represents the set of applied inputs, \(\delta\) represents a quantization or threshold function Haider et al. (2017), and w represents some real weights that are updated in each iteration until an optimal difference (also known as cost function), usually in mean-squared error (MSE) Haykin et al. (2009), is achieved. The cost function is given by Eq. 3.

$$\begin{aligned} y_k = \delta \left( \sum _{j=0}^{M}w_{kl}^{y} \delta _H\left( \sum _{j=0}^{M}w_{ij}^{H}P_R\right) \right) \end{aligned}$$
(2)
$$\begin{aligned} \phi =\frac{1}{2} \sum _{k=1}^{M}(y_k - d_k)=\frac{1}{2} \sum _{k=1}^{M}e_{k}^{2} \end{aligned}$$
(3)

where \(y_k\) is the \(k^{th}\) output value, and \(d_k\) represents the expected value.

Fig. 2
figure 2

Structure of fully connected feed-forward neural network with a single hidden layer

Full size image

From literature we know that while a simple perceptron (a neuron without hidden layers) conveniently classifies AND, NAND, OR, NOR, and NOT gates, it is not able to classify XOR and XNOR gates Yanling et al. (2002). To be able to build a generic structure, it is obvious to choose the solution that could classify all the gates with no exceptions—a multilayer perceptron (MLP) (having one or more hidden layers), presented in Fig. 2. Apparently it seems to add an overhead to have used an MLP for the operators other than XOR and XNOR, but considering the fact that only one cell will replace seven, this overhead seems affordable. In the next section, we will describe design of the logic cell built on an MLP.

Related work

Reconfigurable ALU implementations on CMOS

Reconfigurable computing turns out to be a revolutionary methodology for computational logic while forming new architectures by decreasing area, power and speed overheads. Various architectures were proposed in this regard that were based on re-configurability using the FPGAs Laxmi et al. (2012), a few of which made use of ANN, but unfortunately could not yield much impressive results Rafid and Saad (2009). A ternary ALU (using three-state clock cycle) was introduced with faster computations Haidar et al. (2008). Another ANN-based reconfigurable ALU was designed for digital signal processing applications with functions of additions, subtraction, multiplication, division, power, denoising (sine) and denoising (Gausian) Basu et al. (2015). It compromised on area but improved power and throughput. The design of a 32-bit ALU was proposed that allowed low-power consumption. The technique resulted in 18\(\%\) reduction in power dissipation for 180 nm bulk CMOS technology, with a slight degradation in performance. In addition, there was a reduction in standby leakage power of 22 and 23\(\%\) lower peak current Chatterjee et al. (2005). A reversible ALU was also proposed in literature to reduce propagation delay by 1 ns as compared to the conventional 1-bit ALU Mahayadin et al. (2014).

ALU implementations on QCA

A QCA based 1-bit ALU was proposed with logic operation \(\wedge\), \(\vee\), \(\lnot\), and arithmetic functions of addition (\(\sum\)) and subtraction (\(\lnot \sum\)) using QCA-Designer. The ALU measured 1.67 \(\upmu \mathrm{m}^2\) in area, and incurred a latency of 9 clock cycles Gupta et al. (2012). Similarly, several other ALU implementations were presented; a few of those targeted smaller area, while the others opted for reduced latency Gupta et al. (2013); Ganesh (1824); Misra et al. (2016); Sen et al. (2012, 2014); Patidar et al. (2013); Kanimozhi (2015); Patidar and Tiwari (2014). There had been various implementations for adders and other combinational modules too. Different types of adders like carry flow adder, carry look-ahead adder, and ripple carry adder were implemented to achieve minimum area and power overhead, and minimum propagation delay Cho and Swartzlander (2007, 2009); Pudi and Sridharan (2012); Sultana et al. (2015). Reversible logic was also used to design 1 and 4-bit adders, which claimed to have achieved lower propagation delay as compared to previous implementations by a half clock cycle Kunalan et al. (2014). That 1 bit adder cost an area of 0.67 \(\upmu \mathrm{m}^2\) and four clock cycles of latency. We believe, if a complete ALU was implemented using this reversible logic (with circuits for subtractor and other logic gates, etc.) it would have resulted in a substantially increased area and power overhead, beside yielding greater latency as compared to other ALUs.

In Sect. 4, we will present a comparison of the available ALUs for QCA. Generally, it is difficult to compare the available works in terms of area utilization and latency, since either they are different sized, or do not have a provision for a few logic operations. For example, most of the designs summarized in Sect. 4, did not include a mux to choose one result amongst various arithmetic and logic operations. To get a fair comparison, all the ALUs are first required to be scaled; we have taken a liberty to complete the ALUs with all seven logic, two arithmetic operations, and a mux that chooses result of the desired operation ourselves. In Sect. 4, we will demonstrate that the mux we have designed and augmented with the existing ALUs, is also more area efficient than a few existing ones.

In another work Beigh et al. (2013), the authors presented seven different implementations for an XOR gate, each with a different latency in terms of clock cycles, different complexity level, and a different number of cell count. The authors pointed out that the QCA-based designs were very much dependent on routing and cells placement.

Proposed methodology and system design

As mentioned already, the designers working with the QCA paradigm are required to manually perform the optimization of digital circuits, in terms of both area and latency. We believe that ANN can play a vital role through the diversity in a perceptron, as discussed above, in circumventing this outstanding problem with QCA. For example, in case of an ALU, instead of having two separate blocks for logic and arithmetic computations, the dynamically reconfigurable ALU (DR-ALU), built on the proposed logic cell, will only require one block that may be reconfigured to perform the desired operation as needed. We expect that our proposed approach, besides resulting in a much smaller circuit, will make routing easy both in CMOS and QCA technologies.

The MLP model shown in Fig. 3 classifies all the logic operations successfully, once provided with a unique and correct set of weights (\(w_{ij}\)) and biases (\(b_i\))—together called ANN’s coefficients—for the desired operation. This model is equivalent to a 1-bit logic cell, which is supposed to perform all logic operations between two 1-bit operands (and therefore, needs to be replicated n times for an \(n-bit\) architecture). Note that this perceptron comprises a few threshold functions (\(\delta\)) along with a few multipliers and adders. In this work, we have made use of hardlim and purelin as the threshold functions mainly due to their simplicity, especially in terms of hardware. They, respectively, stand for the following:

$$\begin{aligned} \delta _i(n) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {for } \; n \ge 0 \\ 0 &{} \quad \mathrm{else} \end{array}\right. } \end{aligned}$$
(4)
$$\begin{aligned} \delta _i(n)=n \end{aligned}$$
(5)

Training an ANN model immensely relies on randomly generated coefficients that typically belong to the set of real numbers; the latter may have a severe effect on the resulting hardware, especially those comprising multiplication operations. This also includes the possibility of acquiring floating point numbers. From our digital design background, we realize that a system built to handle floating point numbers is way more complex than its equivalent for the fixed point numbers. This compels us to come up with a novel algorithm that first controls the randomness in the generated weights and biases, and then restricts them to be as small integers as possible to minimize the storage and processing requirements in the hardware. In what follows, we present our methodology, based on a genetic algorithm (GA), to estimate these parameters, followed by manual optimization of the perceptron suitable for binary logic, and QCA implementation of the resulting Boolean expression.

Fig. 3
figure 3

Proposed perceptron

Full size image

GA framework

GAs are biologically inspired stochastic search algorithms, which guide a population of possible solutions toward an optimal solution based on the principle of survival of the fittest. In our proposed framework, set of weights and biases is represented by a string called chromosome, which is replicated to generate a population of given size. For each iteration, fitness is calculated to achieve minimum mean squared error by following fundamental GA operations which include crossover, mutation, and selection. A brief description of each operator used is given below.

Arithmetic crossover operator

Selecting a pair of chromosome \(C^{1}_{i} = (G^{1}_{1}, G^{1}_{2},\ldots , G^{1}_{m} )\) and \(C^{2}_{i}\) \(= (G^{2}_{1}\), \(G^{2}_{2},\ldots ,G^{2}_{m} )\) for an arithmetic crossover description. An Offspring pair is generated, \(O^k = (g^{k}_{1}, g^{k}_{2},\ldots ,g^{k}_{m})\), \(k = 1,2\) where: \(g_i^1 = \lambda G_{i}^{1} + (1- \lambda )G_{i}^{2}\) and \(g_i^2 = \lambda G_{i}^{2} + (1- \lambda )G_{i}^{1}\). \(\lambda\) is chosen to be a constant operator (\(\lambda = 0.5\)) but can vary with the number of generations as in non-uniform arithmetic crossover Jin et al. (2017).

Mutation operator

Under the same consideration as above, let \(R_{\mathrm{max}}\) be the maximum number of generations and \(R_t\) be a generation on which mutation Ginley et al. (2011) is applied, then:

$$\begin{aligned} G_i^{'} = {\left\{ \begin{array}{ll} G_i + \delta (t, \kappa _i - G_i) &{} \quad \text {if } \; G_i = 0 \\ G_i + \delta (t, G_i - \tau _i) &{} \quad \text {if } \; G_i = 1 \end{array}\right. } \end{aligned}$$
(6)

where \(\kappa _i\) and \(\tau _i\) are selected to be 0 and 1 with a probability of 0.1.

Selection

Chromosome with smallest cost function value is selected where the selection rate (\(\varsigma _{\mathrm{rate}}\)) defines the number of survivors need to mate in the next generation. Generally, \(\varsigma _{\mathrm{rate}}\) is selected to be \(50\%\) of the total population Razali et al. (2011).

$$\begin{aligned} \eta _{\mathrm{rem}} = \varsigma _{\mathrm{rate}} \times \eta _{\mathrm{pop}} \end{aligned}$$
(7)
$$\begin{aligned} \eta _{\mathrm{keep}} = \eta _{\mathrm{pop}} - \eta _{\mathrm{rem}} \end{aligned}$$
(8)

The selection probability depends on the cost weight, calculated as

$$\begin{aligned} P_{k} = \frac{C^{k}}{ \sum _{j = 1}^{\eta _{\mathrm{keep}}}C^{j}} \end{aligned}$$
(9)

Generation of weights and biases

Selection of the most optimum features in a finite solution space is very hard, especially with traditional binary-coded GA, which is prone to select N/2 number of features. Each chromosome from a population needs to fulfill the fitness criterion, which is the basis for the selection process. All chromosomes/individuals with better fitness value will have a better breeding chance compared to the individual with lower fitness value. In experimental results, it is suggested not to keep the selection criterion very harsh, so as to ensure the presence of individuals with lower fitness value which undoubtedly increases the population diversity.

Let \(\Psi ^m_{\mathrm{pop}}\) be the assembly of all generated chromosomes having m feature components. The primary goal is to select the offsprings with highest fitness from solution space \(\Psi = \Psi _{m=1}^{N} \Psi _m\). The randomly generated chromosome, \(G_i^m \subseteq [-R_{min} \le C_k \le R_{\mathrm{max}}]\), where \(R_{\varrho }\) is the chromosome’s range in integers, between − 3 and 3. Population is generated based on Gaussian distribution, within the given range.

$$\begin{aligned} \eta _k^m = \mathrm{round}(\mathrm{range}( \mathbb {N}(m; \mu _k,\sigma ^2)\in G_i^m; \mathbb {R}^2 )) \end{aligned}$$
(10)

Considering all above parameters, we come up with a hybrid solution, Algorithm 1, which consolidates two different domains to generate a chromosome with best fitness value, which should have a minimal effect on the resulting hardware. It has two primary units; (1) generation of GA optimized coefficients; (2) ANN trained model which utilizes optimal combination of weights and biases generated in step 1 to perform seven logic operations.

figure b

Table 2 shows all the weights and biases generated by our algorithm for each of the logic operation. It may be conveniently verified that these values, once applied on the MLP, correctly classify the corresponding logic operation.

Table 2 ANN generated weights and biases for the MLP
Full size table

Manual optimization

Let each threshold function, \(\delta (X)\), in Fig. 3 represent a neuron \(N_k^{h}\): then the input to each neuron i in the hidden layer will be one of \(m_{ij}=b_i + w_{i1}P_1 + w_{i2}P_2\), where \(j \in \{1 \rightarrow 4\}\) for four possible binary combinations of two 1-bit operands \(\Theta ^{\{0, 1\}}\). The description of hardlim suggests that output \(\alpha _i\) for each neuron in the hidden layer will be low for negative numbers, and high otherwise, which requires the circuit to simply check the sign bit—usually the left-most bit in the bit-vector, also termed as the most significant bit (MSB). Therefore, the input to each neuron in the hidden layer may now be simplified to \(m_{ij}=\mathrm{MSB}(b_i + w_{i1}P_1 + w_{i2}P_2)\), which is either logic-1 or logic-0 depending upon the applied inputs—enabling us to completely get rid of the costly multiplier and adder, and replace them with a much simpler mux. Similarly, input to the neuron \(N_i^{\mathrm{out}}\) in the output layer of the given perceptron will be \(m_{3j}=\mathrm{MSB}(b_3 + w_{31}f_1 + w_{32}f_2)\).

Extending the reconfigurable logic cell to incorporate the arithmetic unit merely requires extension in number of inputs of the mux; i.e., in addition to the logic operations, neuron-1 and neuron-2 will now compute {sum (S), difference (D)} and {carry (C), borrow (B)} respectively as well. This resorts to the following set of equations for a full adder (that generates S and C) and a full subtractor (that generates D and B): \(S=A'B'C + AB'C + ABC' + ABC\), \(C = A'BC + ABC + AB\), \(D = A'B'C + AB'C + ABC' + ABC\), and \(B = AB'C + ABC + A'B\), where A and B represent the two 1-bit operands, and C is exclusively needed by the arithmetic operations. Following the manual optimization of the equations, \(f_1\), \(f_2\), and Output give the expected Boolean expressions for neuron-1, neuron-2, and neuron-3 respectively, which we need to implement on QCA.

$$\begin{aligned} f_1 = \lnot P_1(\lnot P_2~m_{11} + P_2~m_{12}) + P_1(\lnot P_2~m_{13} + P_2~m_{14}) \end{aligned}$$
(11)
$$\begin{aligned} f_2 = \lnot P_1(\lnot P_2~m_{21} + P_2~m_{22}) + P_1(\lnot P_2~m_{23} + P_2~m_{24}) \end{aligned}$$
(12)
$$\begin{aligned} \mathrm{Output} = f_1(f_2~m_{31} + \lnot f_2~m_{32}) + \lnot f_1(f_2~m_{33} + f_2~m_{34}) \end{aligned}$$
(13)

Table 3 summarizes the optimized input to each neuron as per the desired arithmetic or logic operation. The table should be interpreted as follows: for the two operands 00, if the desired operation is AND, the inputs to neuron-1 (\(m_{11}\)), neuron-2 (\(m_{21}\)), and neuron-3 (\(m_{31}\)) should be 0, 1, and 0 respectively, and so on.

Table 3 Optimized entries for neuron-1, neuron-2, and neuron-3
Full size table

QCA implementation

Since the primary contribution of this work is to come up with a set of optimized Boolean expressions, by means of ANN and an optimization algorithm, for the DR-ALU, we will not argue on the optimal number of QCA cells required for its implementation. This discussion is beyond the scope of this work, and is deliberately left as a prospective research direction. However, for the sake of showcasing the applicability and effectiveness of the proposed optimization methodology, in what follows we present one, carefully developed, implementation on QCA. In Sect. 4, we will present the detailed comparison of this implementation with a few existing ones in the literature.

The most commonly used tool for accurate description of QCA-based digital circuits and their verification is QCA-Designer (QCAD) Watanabe et al. (2002). To this end, we have made use of the said software for the description of 1-bit DR-ALU for QCA, which has been tested and simulated using bi-stable approximation simulation engine. For wire-crossover, we have employed the multilayer crossover technique instead of coplanar crossover Perri et al. (2012); Huang et al. (2004), since our target has always been the smaller number of QCA cells; and hence the smaller area. Figures 4 and 5 present the multi-layer implementation of the DR-ALU obtained from the optimized Boolean expressions. Any QCA–ALU, built on the proposed logic cell, should require smaller number of QCA-cells, and therefore, yield smaller area on the die. The simulation results and other attributes of the proposed design will be discussed in the next section.

Fig. 4
figure 4

Proposed QCA logic cell: main layer

Full size image
Fig. 5
figure 5

Proposed QCA logic cell: second layer

Full size image

Simulation results

QCAD simulations and results

Figure 6 presents the proposed mux that we have augmented with various available QCA–ALUs to be able to carry out a fair comparison. Note that all of our QCA simulations are done on QCAD using the design parameters given in Table 4. Table 5 shows a comparison of the proposed mux (Prop) with a few available in literature. Clearly, our design stands out as the most efficient one—further strengthening our claim of unavailability of standard design procedure for QCA.

Fig. 6
figure 6

Proposed multiplexer

Full size image
Table 4 Design parameters for QCAD simulations
Full size table
Table 5 Comparison of 4-input mux
Full size table

Although, we have rigorously simulated the designed DR-ALU for each arithmetic and logic operation, here we can only present a subset of those simulations due to limited space. Figure 7 shows the behavior of a full-adder with \(f_1\) and \(f_2\) being the carry-out and sum outputs, respectively. Similarly Fig. 8 shows the simulations for an XOR gate.

Fig. 7
figure 7

QCAD simulation of the full adder

Full size image
Fig. 8
figure 8

QCAD simulation of the XOR gate

Full size image

It has already been mentioned that latency of the QCA circuits is measured in terms of clock cycles. In the proposed DR-ALU, we have a different latency for each of the logic and the arithmetic units, since the latter does not use the output layer neuron. While latency for the logic unit is four clock cycles, for the arithmetic unit it is estimated to be two. Most of the previously proposed QCA–ALUs, despite not offering the complete functionality, have a latency greater than the proposed one. Table  6 summarizes the relevant benchmark works (ref.), their architectures (arch.), along with the functionality they offer and the results they achieve in terms of cell-count, latency, and area utilization. The table also lists the same for the proposed work (Prop).

Clearly, the works Ganesh (1824) and Sen et al. (2014) are the closest to the proposed, except for the fact that they both lack two functions, and the former does not have the mux for choosing the final result in addition. The enormous difference in the area utilization between those works and the proposed is mainly due to the multi-layer wire-crossing technique we have employed: it is complicated, but more area efficient.

Table 6 Comparison of the existing QCA–ALUs with the proposed one
Full size table

Note that for a fair comparison, we have augmented our own mux, Fig. 6, with those ALUs not having it already, and redesigned each of them to have all the logic and arithmetic operations as the proposed one. Now the comparison, in terms of area utilization, is given in Fig. 9. It is evident that for an identical set of operations, the proposed work is significantly smaller than the benchmark works.

Fig. 9
figure 9

Comparison of area of the proposed DR-ALU with the existing designs: a Gupta et al. (2012), b Gupta et al. (2013), c Ganesh (1824), d Misra et al. (2016), e Sen et al. (2012), f Sen et al. (2014), g Patidar et al. (2013), h Patidar and Tiwari (2014), i Pandimeena et al. (2017), j Prop

Full size image

FPGA implementation and synthesis

As the last exercise, what remained to be evaluated was that our ANN and GA based optimization had not altered the original functionality of the ALU. We implemented the optimized Boolean expressions on an FPGA from Xilinx, performed equivalence checking, and ran several simulations for each logic and arithmetic operation. Figures 10 and 11 present two sample simulations: while the former corresponds to arithmetic unit, the latter presents simulations for each logic operation. Besides being functionally correct, our FPGA synthesis yielded 40\(\%\) reduction in area as compared to a CMOS–ALU designed by a usual behavioral description.

Fig. 10
figure 10

FPGA simulation of the arithmetic unit

Full size image
Fig. 11
figure 11

FPGA simulation of the logic unit

Full size image

Conclusion

The state-of-the-art in quantum-dot cellular automata (QCA) lacks in a standard implementation methodology for digital circuits in general, and an arithmetic and logic unit (ALU) in particular. This quagmire has led to several vastly different implementations for ALU—each advocating its merits, usually in terms of cell-count, area utilization, and latency. In this work, we have attempted to address this issue by proposing an optimized set of Boolean expressions, which we have called a dynamically reconfigurable (DR) logic cell. The cell is capable of reconfiguring itself to perform various arithmetic and logic operations—one at a time—as needed. While the reconfigurability of the cell is achieved by providing a unique set of weights and biases, called coefficients, to a trained artificial neural networks based model, the coefficients themselves have been optimized by means of a genetic algorithm. The optimization technique is meant to control the randomness in the generation of coefficients, so as to obtain only fixed point small integers, which should have a minimal effect on the resulting hardware. We have demonstrated how this cell may be replicated and appositely organized to build a complete DR-ALU, which is much smaller than the existing equivalents. In addition to this, we have proposed a novel multiplexer, which is also more area efficient as compared to several existing works.

Autonomously determining the minimal number of QCA cells to implement a given Boolean expression still remains an outstanding research problem. This we have left as a prospective research direction that we intend to address in near future.