Introduction

The reorientation of nematic liquid crystal (LC) molecules in optical fields has been studied extensively in the past decade (Bender et al. 2001; Van Boxtel et al. 2004). Dispersions of LC with nano particles like Pd, Ag, Ag/Pd, inorganic nano particles of MgO, and polymeric nano structures have been a subject of many studies since their introduction as a potential means for bistable liquid crystal displays (Bender et al. 2001; Van Boxtel et al. 2004; Haraguchi et al. 2007). However, the zinc oxide nano particles with 1 % copper doped [ZONPs (1 % Cu)] are also useful for the study of equilibrium conditions in the liquid crystalline systems (Haraguchi et al. 2007; Hoffman et al. 2003).

Apart from calorimetric, NMR study and other techniques dielectric spectroscopy can also investigate certain important untouched aspects of the nanonematic suspensions. The more important aspect of LC research involves selective chemical design of nematic molecules to enhance their electro optic performance (Tschierske et al. 1995; Hourri et al. 2001; Frunza et al. 2001; Rozanski et al. 2006). Dielectric experimental studies of nematic LCs can provide information about the molecular arrangement, intermolecular interaction and the dynamics of reorientational motions. This information is useful in designing of a nematic LC device and more particularly for twisted nematic displays (Jadzyn and Żywucki 1987; Huch et al. 2002; Xu et al. 2009).

The ZONPs (1 % Cu) have attracted interest of researchers in the recent past due to their excellent chemical and physical properties. ZONPs (1 % Cu) have a wide range of applications in piezoelectric transducers, photonic crystals, photo detectors, photodiodes, light emitting devices, transparent conductive films etc (Sharma et al. 2009). One of the emerging research areas is the ZONPs (1 % Cu) composite, where the performance of the host material can be significantly improvised by the addition of a small amount of ZONPs (1 % Cu). The dispersion and alignment of ZONPs (1 % Cu) may be an important issue in improving mechanical, thermal, electrical and optical properties of host materials such as polymers and LCs. The ZONPs (1 % Cu) have a large band gap at room temperature (3.37 eV) (Sharma et al. 2009; Wang et al. 2008). It has a spontaneous polarization along the C- axis and has the wurtzite structure. The interaction between LC molecules and the ZONPs (1 % Cu) leads to a number of changes in the properties of liquid crystalline phases (Sharma et al. 2009; Wang et al. 2008; Wang 2004; Omar et al. 2009).

Recently considerable experimental results have been reported to elucidate the anisotropy ordering mechanism of LCs using dielectric spectroscopy. Investigations involving the measurement of temperature variation of the dielectric anisotropy, dielectric permittivity, relaxation strength and relaxation time in the nematic phase provide valuable information regarding the nematic orientational order and the growth of dipole correlation (Merkel et al. 2006). Most of these studies are generally with the 5CB, E49, MBBA etc in their pure and doped forms with different doping particles (Van Boxtel et al. 2004; Lynch and Patrick 2002; Prasad et al. 2006). Therefore, we have conducted comparative study of the highly polar and weakly polar liquid crystal with their pure and nano particles doped forms to examine advantage and disadvantage of ZONPs (1 % Cu) doping, more particularly by choosing different type of LCs in terms of their dipole moments. The measurements were performed on two molecules namely 5CB and D6AOB with their 1 % w/w ZONPs (1 % Cu) suspension. We have studied the dynamics of molecules particularly in terms of the dielectric permittivity, relaxation frequency and dielectric anisotropy.

Experimental details

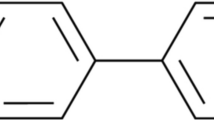
ZONPs (1% Cu) doped LC suspension of a nematic LC host; 4, 4′-pentyl cyano biphenyl (5CB) and dihexyl azoxy benzene (D6AOB) have been used for the present investigations. The molecular structure and nematic to isotropic transition temperature of these nematics are given in the Fig. 1.

Fig. 1
figure 1

Molecular structure of LCs used for study a 5CB nematic with transition scheme b D6AOB nematic with transition scheme

Full size image

The 5CB is a well explored LC which is used for the present study (Leys et al. 2008). It has a Cyano group at its one end, which makes it a highly polar molecule. The alkyl chains on each side of the D6AOB molecules provide an added advantage that the deviation of the molecular long axis from the direction of the applied field is to be minimal. The dipole moment in D6AOB has the magnitude of 1.70 D making an angle of 64.9° from the long molecular axis (Sinha et al. 2004). The host materials have been purchased from Frinton Laboratories USA and used as sample.

The nanoparticles (Provided by the Nano Phosphor Centre, Physics Department, University of Allahabad, Allahabad 211002, India) were synthesized by a chemical technique based on hydrothermal method (Sharma et al. 2009). The crystallite sizes, estimated by XRD were found to be nearly 14 nm, whereas TEM/SEM (Tunneling Electron Microscopy/Scanning Electron Microscopy) studies indicated the formation of uniform nanorods. At room temperature, nanoparticles of ZnO are wide band gap (3.37 eV) semiconductor and also have the piezoelectricity (Sharma et al. 2009).

We have used planar as well as homeotropic alignment of LCs for our dielectric studies. The sandwiched type (parallel plate capacitor) cells were made using two optically plane glass substrates coated with conducting ITO (Indium Tin Oxide) layers. To obtain planar alignment the conducting layer were treated with the Silane solution (0.2 % solution of phenyl trichloro silane in tolune) as adhesion promoter and coated with polymer nylon (6/6). Nylon 6/6 purchased from Acros Organics USA. Nylon 6/6 solution has been prepared by dissolving 0.5 % Nylon wt/wt of the volume of the solution 10 % methanol and 60 % m-cresol. After drying the polymer layer, two substrates were rubbed unidirectionally by a velvet cloth. The substrates were then placed one over another to form a capacitor. The cell thickness was fixed by placing a Mylar spacer (10 μm in our case) in between and then it was sealed by a UV sealant. To obtain homeotropic alignment, the substrate were cleaned with acetone, and then simply coated with the solution of Lecithin (cetyl trimethyl ammonium bromide dissolved in ethyl alcohol). The substrates have been dried at 200 °C for 10 h before assembling the cell (Manohar et al. 2007; Srivastava et al. 2007; Misra et al. 2008). The empty sample cells were calibrated using analytical reagent (AR) grade CCl4 and benzene as standard references for dielectric studies. The LC’s suspension was prepared by non-synthetic chemical method in the weight ratio 1:100 (i.e. 1 % concentration of nanoparticles in nematic liquid crystal). The assembled cells were filled with the suspension and pure LCs at a temperature 10 °C higher than the isotropic temperature of the liquid crystal by capillary method.

Dielectric measurements were carried out using a computer controlled impedance Gain/Phase analyzer (HP 4194A) attached with a temperature controller in the frequency range 100–40 MHz. The dielectric measurements have been carried out as a function of temperature by placing the sample on a computer controlled hot plate (HCS-302, INSTEC Co. USA). The temperature stability was better than ± 0.1 °C. The data obtained at higher frequencies were strongly affected by the ITO relaxation, therefore data at higher frequencies (f > 10 MHz) was corrected (Srivastava et al. 2007; Misra et al. 2008).

The dielectric relaxation phenomena for both the samples in nematic phase have been examined using Cole- Cole relation. The Cole–Cole (Cole and Cole 1941), equation is given by

$$ \varepsilon^{*} = \varepsilon^{{\prime }} \left( \infty \right) + \frac{{\delta \varepsilon^{{\prime }} }}{{1 + \left( {j\omega \tau } \right)^{1 - \alpha } }} $$
(1)

where \( \delta \varepsilon^{{\prime }} \) is the dielectric strength of the relaxation and \( \varepsilon^{{\prime }} \left( \infty \right) \) is the high frequency limit of the relative dielectric permittivity, ω(=2πf) is the angular frequency, τ is the relaxation time and α is the distribution parameter.

The low and high frequency deviations in dielectric data require correction for low and high frequency values (Srivastava et al. 2007; Misra et al. 2008). On separating the real and imaginary part of the Eq. (1) one may get

$$ \varepsilon^{{\prime }} = \varepsilon^{{\prime }} \left( {\text{dc}} \right)f^{ - n} + \varepsilon^{{\prime }} \left( \infty \right) + \frac{{\delta \varepsilon^{{\prime }} \left[ {1 + \left( {2\pi f\tau } \right)^{{\left( {1 - \alpha } \right)}} \sin \left( {{{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } 2}} \right. \kern-0pt} 2}} \right)} \right]}}{{1 + \left( {2\pi f\tau } \right)^{{\left( {1 - \alpha } \right)}} + 2\left( {2\pi f\tau } \right)^{{\left( {1 - \alpha } \right)}} \sin \left( {{{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } 2}} \right. \kern-0pt} 2}} \right)}} $$
(1a)

And

$$ \varepsilon^{{\prime \prime }} = \frac{{\sigma \left( {\text{dc}} \right)}}{{\varepsilon_{0} 2\pi f^{k} }} + \frac{{\delta \varepsilon^{{\prime }} \left[ {1 + \left( {2\pi f\tau } \right)^{{\left( {1 - \alpha } \right)}} \cos \left( {{{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } 2}} \right. \kern-0pt} 2}} \right)} \right]}}{{1 + \left( {2\pi f\tau } \right)^{{2\left( {1 - \alpha } \right)}} + 2\left( {2\pi f\tau } \right)^{{\left( {1 - \alpha } \right)}} \sin \left( {{{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } 2}} \right. \kern-0pt} 2}} \right)}} + {\text{Af}}^{m} $$
(1b)

Here σ(dc) is the ionic conductance and ε o is the free space permittivity; k, A and m are the fitting parameters; α is the distribution parameter and ω is the angular frequency. The term \( \varepsilon^{{\prime }} {{\left( {\text{dc}} \right)} \mathord{\left/ {\vphantom {{\left( {\text{dc}} \right)} {f^{ - n} }}} \right. \kern-0pt} {f^{ - n} }} \) and \( \sigma {{\left( {\text{dc}} \right)} \mathord{\left/ {\vphantom {{\left( {\text{dc}} \right)} {\varepsilon_{\text{o}} 2\pi f^{k} }}} \right. \kern-0pt} {\varepsilon_{\text{o}} 2\pi f^{k} }} \) are added in the above equation for the low frequency effect due to the electrode polarization, capacitance and ionic conductance. The term \( {\text{Af}}^{m} \) is added in Eq. 1b for the high frequency effect due to the ITO resistance and lead inductance. By the least square fitting of above equation into the experimental data we have removed the low and high frequency errors (Manohar et al. 2007; Srivastava et al. 2007; Misra et al. 2008). The fitting parameters are n and α for dielectric permittivity and k, α, A and m for loss.

Result and discussion

In order to study the influence of the ZONPs (1 % Cu) on the rotational motions of the molecules of the pure liquid crystal, the dielectric relaxation spectra were obtained for D6AOB and 5 CB in their pure and 1 %wt/wt nano particles doped forms. The real and imaginary parts of the dielectric permittivity (\( \varepsilon^{{\prime }} \) and \( \varepsilon^{{\prime \prime }} \)) of D6AOB and 5CB were measured at 30 °C, as a function of frequency for homeotropic orientation i.e. \( \varepsilon_{\parallel } \) (electric field parallel to the molecular director) and planar orientation i.e. \( \varepsilon_{ \bot } \) (electric field perpendicular to the molecular director) and are shown in the Figs. 2 and 3, respectively. The relaxation processes in D6AOB and 5CB are qualitatively different. The D6AOB sample in pure and doped forms show two molecular relaxations for the homeotropic alignment (as indicated by arrows in the Fig. 2a, b). The 5CB sample shows only one clear molecular relaxation in the pure and doped form for both homeotropic as well as planar alignment.

Fig. 2
figure 2

Real (permittivity) and imaginary (loss) part of dielectric permittivity (\( \varepsilon^{{\prime }} \) and \( \varepsilon^{{\prime \prime }} \)) as a function of frequency in homeotropic alignment for D6AOB (a, b) and 5CB (c, d) molecules in their pure and doped form

Full size image
Fig. 3
figure 3

Real (permittivity) and imaginary (loss) part of dielectric permittivity (\( \varepsilon^{{\prime }} \) and \( \varepsilon^{{\prime \prime }} \)) as a function of frequency in planar alignment for D6AOB (a, b) and 5CB (c, d) molecules in their pure and doped form

Full size image

The dielectric permittivities of pure D6AOB and pure 5CB have decreases when doped with ZONPs (1% Cu) as shown in Figs. 2 and 3. The decreasing in the dielectric permittivity for D6AOB is very little. This decreasing nature of permittivity may be explained only on the basis of presence of Cu ion in the nanoparticles and size of the nanoparticles (Manohar et al. 2009). This is due to the small dipole moment of D6AOB comparison to 5CB. Copper ion greatly helps towards the charge transportation in the suspension. The electronic charge transfer takes place through nanoparticles. The nanoparticles have the length 14 nm whereas the liquid crystal molecules have the length in the order of tenth of nanometers (Sinha et al. 2004; Sinha and Aliev 1998; Oka et al. 2004). Due to the large size of nanoparticles the distance of hopping between the neighbouring nanoparticles sufficiently decreases. This provides an easier way of ionic charge transfer mechanism, i.e., charge transfer through nanoparticles. The distance of hopping is a minimal distance between the nanoparticles (Manohar et al. 2009).

The frequency dependences of the dielectric permittivity for ZONPs (1 % Cu) doped D6AOB in the nematic phase for homeotropic alignment are shown in Fig. 2a, b, which gives typical relaxation spectra observed in nematic phases with homeotropic alignment (Sinha et al. 2004; Oka et al. 2004). The strong dependence of frequencies of the processes corresponding to the rotations around short and long molecular axes are well known in general for the LCs (Sinha et al. 2004; Sinha and Aliev 1998; Oka et al. 2004). In the D6AOB the molecular relaxation at the characteristic frequency 0.96 MHz is due to the rotation around their short axis and is a slow process. The other relaxation process around 10 MHz is due to ITO relaxation which is not taken into account. In earlier reported papers it is given that the next relaxation process in D6AOB is the fast process and lie in the GHz region (Sinha et al. 2004; Oka et al. 2004). This relaxation is going out of range in our experiment. The ZONPs (1 % Cu) have little influence on the relaxation processes of D6AOB in the doped sample. Both the processes in pure and ZONPs (1 % Cu) doped samples for both nematics are quite similar. It can be inferred that the strength of the dipole moments has small or may be no influence on the relaxation frequencies (Merkel et al. 2006; Sinha and Aliev 1998; Oka et al. 2004; Rahman and Lee 2009). This is also clear from the relaxation frequency versus temperature curves as discussed later. In 5CB the only process is that the molecular rotation around the short molecular axis is at the characteristic frequency of 0.99 MHz. The 5CB has a dipole moment (located in the –CN terminal group) that is mainly oriented along the long molecular axis. In 5CB the angle between the long molecular axis and dipole moment is only 7.9°; the major contribution of dipole moment is towards the long molecular axis (Sinha et al. 2004; Sinha and Aliev 1998; Yadav et al. 2011; Heng et al. 2008).This means that when the probing electric field lies in the same direction as the nematic director, the relaxation spectrum is dominated by the process associated with the rotation of the molecule around the short molecular axis.

The molecular relaxation spectra for planar orientation of samples are shown in Fig. 3. In case where the director is perpendicular to the field, no molecular relaxation process in the doped D6AOB has been observed. In the case of 5CB in the pure and doped forms, typical relaxation spectra were obtained. It is observed that the relaxation process in pure 5CB is obtained at the characteristic frequency 9.3 MHz. For doped 5CB sample this process is observed at characteristic frequency of 5.3 MHz. In planar alignment the probing electric field is perpendicular to the nematic director and mostly contributions related to the perpendicular component of the dipole moment will be probed (Sinha et al. 2004; Sinha and Aliev 1998; Oka et al. 2004). However as this component is small in 5CB, the perpendicular relaxation process is often interpreted as librational motion of the molecule around the director and not as the rotation around the long molecular axis. In the case of 5CB doped with ZONPs (1% Cu) the disorder produce in the system due to presence of nanoparticles. Now the LC molecule decreases their librational motions. Therefore the relaxation shifts somewhat lower side of frequency as shown in Fig. 3c, d (Sinha and Aliev 1998; Oka et al. 2004; Rahman and Lee 2009).

The Fig. 4a, b shows relaxation frequency (f R) of the pure and doped samples against temperature. It is found that the relaxation frequency for doped samples is more than the pure samples in the nematic range. The relaxation frequency increases with the increase in temperature for both samples in their pure and doped form. The addition of nano particle into the liquid crystals system decreases the hindrance for the motion of nematic molecules, which results in increase of the relaxation process and the same reason is accounted for the increase in relaxation frequency with temperature (Leys et al. 2008; Oka et al. 2004).

Fig. 4
figure 4

Relaxation frequency versus temperature curve for the nematic range of D6AOB (a) and 5 CB (b) in their pure and doped form

Full size image

The dielectric anisotropy of both nematic samples decreases when doped with ZONPs (1 % Cu) as shown in Figs. 5 and 6. In pure D6AOB the dielectric anisotropy has the positive value in the nematic range as reported earlier (Sinha et al. 2004; Oka et al. 2004). At 30 °C the dielectric anisotropy has the value 2 for pure D6AOB. The ZONPs (1 % Cu) doped D6AOB shows the decrease in dielectric anisotropy whose value becomes 0.2 in the nematic range. The value of the dielectric anisotropy of pure 5CB is 12 in the nematic range but when it doped with ZONPs (1 % Cu) its value decreases to 9. The reason for this decrement is accounted for the compatibility and nature of the guest particles. The ZONPs (1 % Cu) have dipole moment perpendicular to the surface and along the C-axis (Sharma et al. 2009; Wang 2004). Therefore in the presence of electric field the nanoparticles try to align in the direction perpendicular to the electric field. However liquid crystal molecule will try to align in the direction of electric field. This motion of nematic molecules and ZONPs (1 % Cu) makes disturbances in the system and the system is now more disordered one. These disorders are localized around the ZONPs (1 % Cu). That is the ZONPs (1 % Cu) introduce the isotropization in the pure nematic liquid crystal system. This means that the structure and, consequently also the dynamics, will be driven toward a more isotropic one (Sinha and Aliev 1998; Rahman and Lee 2009; Yadav et al. 2011).

Fig. 5
figure 5

Behavior of dielectric anisotropy as a function of temperature for the nematic range of a D6AOB and b 5CB in their pure and doped form

Full size image
Fig. 6
figure 6

Behavior of dielectric anisotropy as a function of frequency for a D6AOB and b 5CB in their pure and doped form

Full size image

The dielectric anisotropy decreases with the increase in the temperature for nematic range of both the samples as shown in Fig. 5a. But this decrement is clearer in 5CB sample. The dielectric anisotropy of D6AOB almost remains constant in the nematic range at all temperatures. Since it has been shown that the cyanobiphenyls form dynamically antiparallel correlated pairs; the dipoles of the molecules align themselves antiparallel. In 5CB it seems to indicate that the antiparallel associations are broken when the temperature increases. Therefore anisotropy decreases with temperature more clearly in 5CB sample (Leys et al. 2008).

In order to study the frequency response of the nematic dipoles the dielectric anisotropy for both LCs in pure and doped forms has been plotted with frequency in Fig. 6. In the nematic phase both the LCs in pure form exhibit a positive dielectric anisotropy \( \Delta \varepsilon = \varepsilon_{\parallel } - \varepsilon_{ \bot } \) in the large frequency range. The value of dielectric anisotropy for doped D6AOB and 5CB sample at MHz frequency range decreases significantly, suggesting that ZONPs (1 % Cu) affect the parallel and perpendicular component of dielectric permittivity (\( \varepsilon_{\parallel } \) and \( \varepsilon_{ \bot } \)) (Belyaev et al. 2000; Ouskova et al. 2003; Czub et al. 2008). The 5CB sample in the pure and doped form shows the same trend of dielectric anisotropy versus frequency curve and in the MHz region both the graph overlap. This reflects the flat behavior of parallel and perpendicular component of dielectric permittivity in 5CB sample. However dielectric permittivity for doped D6AOB goes from positive to negative before the MHz region. We believe that the reason for the dielectric anisotropy of ZONPs (1 % Cu) doped D6AOB is attributed to the fact of nonlinear shape of D6AOB molecule and geometrical anisotropy of ZONPs (1 % Cu). The geometrical anisotropy of ZONPs (1 % Cu) is not taken into account in the theory of dielectric properties of heterogeneous system (Belyaev et al. 2000; Ouskova et al. 2003).

Conclusion

ZONPs (1 % Cu) doped D6AOB and 5 CB sample shows the decrement in the dielectric permittivity with respect to pure sample. This decrement explained on the basis of charge transportation through the Cu ion and nanoparticles. The ZONPs (1 % Cu) doped D6AOB and 5 CB shows the qualitatively different relaxation spectra in homeotropic and planar alignment. This is explained in the terms of dipole moment contribution along the short and long molecular axis. The dielectric anisotropy of doped samples is found to decrease for both samples because ZONPs (1 % Cu) makes the disorder in the nematic liquid crystal system.