Introduction

Due to their non-linear electrical coefficient or varistor properties, pure and doped ZnO materials attract more and more attention of researchers and industrials (Matsuoka et al. 1969; Subasri et al. 2009).

Such materials are usually used to manufacture devices used for the protection of electrical circuits and electronic devices against voltage surge (Subasri et al. 2009). ZnO is also, widely used in various fields such as piezoelectricity, electronics, optics, photovoltaic, thermal and spintronics (Wood and Austin 1975; Monteiro et al. 2003).

The challenge now is to improve the characteristics of these materials. This is what has led many researchers to study these materials in their nanoscale form on one hand and doping with specific elements on the other hand.

Among several methods of ZnO nanopowder elaboration, the sol–gel is a widely used one; it is a simple method with a low cost on one hand, and a good quality of the obtained powder at room temperature on the other hand. That is why we used this method as a means of synthesizing our powders (Arab et al. 2012; Miao et al. 1996).

Doping ZnO with various elements such as Co and Mn or some oxides such as Bi2O3, Pr6O11, Sb2O, CoO, MnO, Cr2O leads to expand the use of this material to other fields or to improve its performance such as varistor characteristics.

It is important to report that some of these dopants such as Bi2O3, Sb2O3 and Pr6O11 interact generating secondary intergranular phases, while others, such as Co and Mn, pass into solution in ZnO grains (Lin et al. 2007).

Furthermore, much work have been done in electrical properties of ZnO varistors; it is demonstrated that these properties are greatly dependent on the material composition (nature and amount of doping) (Savary et al. 2011a), density of sintered samples (Nahm 2003), grains size (Anas et al. 2012), morphology and distribution of the second phases. It is reported also that the double Schottky barrier formed between two ZnO grains is responsible for the non-ohmic behavior of varistors (Peng et al. 2010; Blatter and Greuter 1986). Besides this Duran et al. (2003) had reported that the breakdown voltage of varistors increased with decrease in grain size and improved with density and doping elements distribution homogeneity.

Although these investigations, there are few works that have either been carried out on systematic study of the effect of cobalt on ZnO varistor effect, using nanocrystalline powders as starting materials, or preventing the grain growth, as much as possible, during the sintering process, which is the aim of this study.

To do this, Co doped ZnO nanopowders were synthesized by means of sol–gel route, and then sintered, as pellets, in microwave sintering, which has the advantage of reducing the grain size and to have dense materials, using a very short time of sintering (Subasri et al. 2009; Savary et al. 2011a).

It is well-established that the addition of cobalt oxides in the matrix of ZnO improves the non-linear properties (Onreabroy et al. 2006; Long et al. 2010; Nahm and Kim 2002; Onreabroy and Sirikulrat 2006). Onreabroy et al. (2006) found that, the ZnO–CoO-based varistor, with an average grain size of 16 µm, have an ohmic behavior at low sintering temperatures (below 1,000 °C), and also at high sintering temperatures (above 1,100 °C). However, at intermediate sintering temperatures (1,000–1,100 °C), the ZnO–CoO-based varistors show a non-ohmic behavior. Unfortunately, they did not calculate the values of the non-linearity coefficient α, which has been investigated in this study.

Several studies (Subasri et al. 2009; Long et al. 2010; Cheng et al.2012; Anas et al. 2010) have investigated the properties of ZnO, doped with different elements-based varistors using various methods, but few works have been devoted to study the properties of ZnO–CoO-based varistors, especially, using the microwave sintering on one hand and to use nanocrystalline powders for manufacturing pellets used for this study on the other hand; it is what gives this study its originality, in which we investigated the influence of grain size and amount of Co on the properties of ZnO–CoO-based varistors.

To do this we synthesized nanopowders, using the sol–gel route.

The obtained powders have been characterized by X-ray diffraction (XRD) and scanning electron microscopy (SEM). Then the nanopowders were pressed by disks with diameter of 15 mm under pressure of 75 MPa and then sintered by microwave. The current–voltage I(V) behavior was measured using a direct current power supply (1,500 V, 10−2A), a Nano-Ampere meter and a Voltmeter. The density and the non-linearity coefficient α of different samples were then calculated.

Experimental

Synthesis

Co-doped ZnO nanopowders with Co varying from 0 to 7 mol% were synthesized by the sol–gel technique. The reagents used are: Zinc acetate dehydrate [Zn (CH3COO)2.2H2O: purity >99 %, Biochem–Chempharma)], Cobalt acetate tetrahydrate [Co(CH3COO)2.4H2O: purity >99 %, Biochem–Chempharma], Lactic acid and Ethanol.

First, the zinc acetate dehydrate and cobalt acetate tetrahydrate are dissolved in ethanol, and then the obtained solution is stirred at 70 °C for 2 h. After that, the lactic acid is dripped into the obtained mixture until obtaining transparent and homogeneous solution. The molar ratio of ethanol to lactic acid is 3. The final solution was then dried at 100 °C for 1 h and calcined in air at 550 °C for 2 h. Finally, a kind of a green nanopowder is obtained.

Sintering

Microwave sintering was carried out in a 2.45 GHz, 850 W microwave furnace (model LG-MC-805AY, South korea- (Fig. 1)). The thermocouple is connected to a circular disk (thickness = 2 cm and diameter = 3 cm) of SiC, which is placed on an alumina support to avoid a probable contamination. On this support is placed the sample to be sintered. The whole is placed in an insulating chamber made of alumina fibers.

Fig. 1
figure 1

Microwave sintering furnace

Full size image

After closing the oven, the following parameters are defined: the sintering temperature given by the thermocouple attached to the magnetron, the sintering time and the chosen power.

Investigations were carried out in air using one chosen sintering temperature.

Characterization

The nanopowders structure was identified by XRD using the Cukα (λ = 0.154056 nm) radiation of a BRRUKER AXS, D8 advence X-ray diffractometer. The density of the sintered samples was measured by means of Archimedes method using a SCALTEC SBC22 analytical weighing balance.

The particle size of the synthesized powders, before and after sintering, their morphology are determined by means of a VEGA TS 5,130 MM, TESCAN scanning electron microscope (SEM).

The average particle size (D) of sintered samples is determined by the lineal intercept method, given by the following equation:

$$D = 1.56\;L/MN,$$

where L is the random line length on the micrograph, M the magnification of the micrograph and N the number of grain boundaries intercepted by the lines (Nahm et al. 2004; Wurst and Nelson 1972).

However, the average of the grain size of the powders is calculated by the Scherer’s equation (Ait Ahcen et al. 2006):

$$d = \frac{{0.9\;\lambda }}{{\Delta\theta Cos\theta \;}}$$

where d is the grain size, λ the X-ray wave length (λ = 1.5418Å), Δθ the full width at half-maximum (FWHM) and θ the Bragg angle.

Finally, the current–voltage I (V) characteristics are measured using a direct current power supply (1,500 V, 10−2A), a Nano-Ampere meter and a Voltmeter. The sintered samples are covered by silver paste and heated at 600 °C for 30 min. The nonlinear exponent (α) is calculated from the empirical relation: J = KEα (Onreabroy et al. 2006), where K is a constant, J and E the current density and electric field, respectively. α is given by: α = (logJ2 − logJ1)/(logE2 − logE1) (Levinson and Philipp 1975), with: J1 = 0.1 mA, J2 = 1 mA, E1 and E2 are the electric fields corresponding to J1 and J2, respectively.

Results and discussion

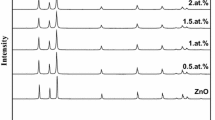
Figure 2 shows XRD patterns of pure and Co doped ZnO nanopowders synthesized by sol–gel technique. The spectra exhibit peaks of the würzite structure, and there are no additional peaks after Co doping, indicating that we have a solid solution for all Co concentrations.

Fig. 2
figure 2

XRD patterns of pure and Co doped ZnO nanopowders

Full size image

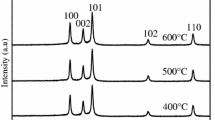
One of intermediate values (Table 1) is obtained with the 5 % mol Co doped ZnO powder. This is why this powder has been chosen for the study as a function of the calcination temperature. The results of the XRD patterns are presented in Fig. 3.

Table 1 Effect of Co concentration on properties of Co doped ZnO varistors
Full size table
Fig. 3
figure 3

X-ray diffraction patterns of 5 % Co doped ZnO nanopowders as a function of calcination temperature

Full size image

The influence of the Co concentration of the varistors made of Co doped ZnO nanopowder on the structural, morphological and electrical properties is shown in Tables 1 and 2.

Table 2 Effect of calcination temperature on characteristics of 5 % mol Co doped ZnO nanopowders
Full size table

The grain size of Co doped ZnO nanopowders decreases by increasing Co concentration as it is shown in Fig. 4, and it reaches its lowest value at nearly 36 nm for 7 % mol% Co.

Fig. 4
figure 4

ZnO nanopowders grain size as a function of Co concentration

Full size image

With regard to the calcination temperature (Fig. 5), it is noticed that the grain size increases with increasing temperature; the values vary from 67 to 168 nm. These results can be connected to the particle size variation, as it is seen in SEM images (Figs. 6, 7), which show that the particle size decreases when Co concentration increases and increases when the calcination temperature increases. Finally, we can say that the grain size and the particle size vary in the same way.

Fig. 5
figure 5

Variation of the grain size of 5 % mol Co doped ZnO nanopowder as a function of calcination temperature

Full size image
Fig. 6
figure 6

SEM images of Co doped ZnO nanopowders: a 1 mol% Co calcined at 550 °C, b 5 mol% Co calcined at 550 °C, c 7 mol% Co calcined at 550 °C, d 5 mol% Co calcined at 650 °C

Full size image
Fig. 7
figure 7

SEM images of sintered samples at 1,075 °C: samples calcined at 550 °C: a 1 mol% Co, b 3 mol% Co, c 5 mol% Co, d 7 mol% Co. e 5 mol% Co calcined at 650 °C andf 5 mol% Co calcined at 750 °C

Full size image

SEM images of Co doped ZnO samples, for different amount of Co, calcined at different temperatures are shown in Fig. 7. All samples have a morphology consisting of particles, uniformly distributed, in the presence of pores, whose number or the porosity of the sample decreases when the concentration of Co increases (Table 1) and increases when the calcination temperature increases (Table 2), which is easily connected to the variations of the grain and particles size. They all vary in the same way.

We can also deduce, from SEM images (Fig. 7), that the rearrangement is achieved more easily for small particles than for larger ones.

Additionally, we observe no second phases between particles, which confirm, once again, that Co atoms pass into solution in ZnO matrix.

Another important result is related to the color of the powders. Figure 8 shows also that the green color becomes darker when the Co concentration increases. The obtained green powders (Fig. 8) consist in particles agglomerated together, which could be easily broken down during pelleting and then used to obtain green pellets uniformly packed.

The calculation of the density of samples sintered at 1,075 °C has confirmed the previous results, since it has been recorded that the density increases with increasing Co concentration (Table 1) and decreases by increasing calcination temperature, as shown in Table 2 for 5 % mol Co doped ZnO, which can also be seen in Figs. 9 and 10, respectively.

Fig. 8
figure 8

Appearance of powders: a commercial pure ZnO powder, b–e green powders prepared by sol–gel, b 1 % Co, c 3 % Co, d 5 % Co, e 7 %Co

Full size image
Fig. 9
figure 9

Density of samples sintered at 1,075 °C as a function of Co concentration

Full size image
Fig. 10
figure 10

Density of samples sintered at 1,075 °C as a function of the grain size

Full size image

For a more complete study, the investigation of the influence of sintering time is recommended. It was not done in this work but it will undoubtedly be the subject of future investigations.

Figure 11 shows the variation, at room temperature, of the electric field as a function of the current density [E(J)] for all samples. The curve can be divided into two regions: the first one (the ohmic region) is known as a high resistance region and the second one (the non-homic region) is known as a very low resistance region.

Fig. 11
figure 11

E(J) characteristics of varistors: a as a function of Co amount, b as a function of the calcination temperature

Full size image

The non-linear electrical behavior given by the coefficient α is due to solid state reactions and formation of potential barriers between grains (Mirzayi and Hekmatshoar 2013). More the curve is pronounced more α is great. The obtained results show that the voltage (electric field E) in the non-linear area increases by increasing Co concentration, thus E increases with decreasing of grain and particle sizes. But the current density is reduced, particularly for the 5 mol% Co samples calcined at different temperatures. This does not prevent the non-linear coefficient α to increase with increasing Co concentration up to 11.62 for 5 mol% Co. We notice, however, that the values for 5 and 7 mol% Co are very close.

The samples of 5 mol% Co sintered at 1,075 °C, show that the non-linear coefficient α decreases by increasing of calcined temperature, therefore increases with decreasing of grain and particle sizes.

Other studies showed that the Co doped ZnO, which particle size is about 16 µm, exhibits a non-linear behavior in the sintering temperature interval [1,000, 1,100 °C].

It is good to remember that the breakdown electric field EB is the field related to the current flowing through the varistor and is equal to 1 mA/cm2 (Sedky et al. 2012; Nahm 2012; Hembram et al. 2011).

The different values of EB can be deduced from curves of Fig. 11. They allowed to calculate the breakdown voltage per grain boundary (Vgb), given by the equation (Anas et al. 2010): EB = Vgb/d and listed in Tables 1 and 2, d being the average of grain size.

It is clear that EB increases with increasing Co concentration, ranging from 71 to 446.5 V/mm. This means that EB ranging from 92.2 to 292.5 V/mm increases with decreasing of the grain size of starting powders. The increase of EB, in both cases, can be explained by the increase of the number of grain boundaries due to the decrease of the grain size average.

Conclusion

Nanopowders of pure ZnO and doped with (0–7 %) mol% Co have been synthesized by the sol–gel route to understand the origin of the varistor effect on this type of nanopowders.

To achieve this goal, powders with grain size below 100 nm were prepared.

The addition of Co up to 7 mol% did not affect the well-known peaks related to würtzite structure of ZnO.

This study permitted us to confirm that the grain size decreases by increasing of the Co concentration and increases by increasing of the calcination temperature.

The use of microwave sintering process allowed us to manufacture varistors with good quality (low density and efficient electrical properties).

The present investigation has also demonstrated that the non-linear coefficient increases by increasing of Co content and grain size.

The great merit of this method remains, undoubtedly, its velocity and the obtaining of ZnO–Co varistors with nano-sized grains.