Mathematical model for the peristaltic flow of Jeffrey fluid with nanoparticles phenomenon through a rectangular duct

Abstract

The study of nanoparticles concentration for the Jeffrey fluid model is considered with the process of peristaltic waves in a three-dimensional rectangular channel. The main theme of the present study is to study the effect of lateral walls on nanoparticle phenomenon in peristalsis with non-Newtonian fluid model in a duct of rectangular cross-section. The flow is considered in a wave frame under the assumptions of long wavelength and low Reynolds number. The resulting three-dimensional nonlinear and coupled partial differential equations are then solved using homotopy perturbation technique. The physical features of lateral walls, mean volume flow rate, Jeffrey fluid parameter, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number are discussed simultaneously through presenting graphical discussion. Three-dimensional phenomenon is also investigated through graphs to see the variation of velocity profile with space coordinates. Trapping scheme is also manipulated with the help of streamlines for various pertinent parameters.

Introduction

Peristalsis is a mechanism of pumping fluids in ducts when a progressive wave of area contraction or expansion propagates along the length of a distensible tube containing fluid. It instigates, in general, propulsive and mixing movements and pumping the fluids against pressure rise. Peristaltic pumping in physiology is an intestine leverage of smooth muscle contraction. It includes the transportation of urine from the kidney to the bladder, food through the digestive tract, bile from the gall-bladder into the duodenum, movement of ovum in the fallopian tube, etc. A significant industrial application of this phenomenon is in the design of roller pumps used in pumping fluids without being contaminated due to the connection with the pumping ordnance (Mishra and Manoranjan 2004). Nanotechnology has fundamental applications in industry since materials of nanometer sized exhibit incomparable physical and chemical characteristics. Water, ethylene glycol and oil are common examples of base fluids used for the nanofluid phenomenon. Nanofluids have their immense contribution in heat transfer like microelectronics, fuel cells, pharmaceutical processes, and hybrid-powered engines, domestic refrigerator, chiller, nuclear reactor coolant, grinding and space technology and many more situations. They reveal enhanced thermal conductivity and the convective heat transfer coefficient counter balanced to the base fluid. Nanofluids have been attracted the attention of many researchers for new production of heat transfer fluids in heat exchangers, in plants and in automotive cooling significations, due to their extensive thermal properties. A large amount of literature is available which deals with the study of nanofluid and its applications (Khanafer et al. 2003; Hakan and Abu-Nada 2008; Wang and Wei 2009). The study of non-Newtonian fluids has obtained the attention of many researchers with the fact that most of the industrial used fluids are non-Newtonian in nature and exhibit nonlinear attitude between stress and deformation rate (see Refs. Naz et al. 2008; Hameed and Nadeem 2007; Patel and Timol 2009; Mekheimer and Abdelmaboud 2008; Mitra and Prasad 1973).

In the field of fluid mechanics, the phenomenon of peristalsis has been considered by a number of researchers due to its valuable applications in medical, physiology, chemical industries and bioengineering. Kothandapani and Srinivas (2008) have analyzed the peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. They have discussed the problem in wave frame moving with a constant axial velocity under the approximations of long wavelength and low Reynolds number. Peristaltic flow of visco-elastic fluid with fractional Maxwell model through a channel has been investigated by Tripathi et al. (2010). They have obtained the analytical solutions with the help of homotopy perturbation method and Adomian decomposition method. Nadeem and Maraj (2012) have more recently described the mathematical analysis for peristaltic flow of nanofluid in a curved channel with compliant walls. Mekheimer et al. (2011) have recently obtained the effect of lateral walls on peristaltic flow through an asymmetric rectangular duct. Reddy et al. (2005) have considered the influence of lateral walls on peristaltic flow in a rectangular duct and observed that the sagittal cross-section of the uterus may be better approximated by a tube of rectangular cross-section than a two-dimensional channel. Mathematical model for the peristaltic transport through an eccentric cylinders has been presented by Mekheimer et al. (2013). Recently, Nadeem et al. (2013) have derived the effects of heat and mass transfer on peristaltic flow of a nanofluid between eccentric cylinders. Keeping in mind the present information, authors come to know that peristaltic flow of nanofluid with non-Newtonian base fluid has not been discussed in a three-dimensional rectangular channel.

So the main idea of the present analysis contains the analysis of peristaltic flow of non-Newtonian Jeffrey fluid model with nanoparticles phenomenon in a rectangular duct. The flow is observed in a wave frame moving with a constant speed c in the axial direction of the flow. The governing equations are formulated under the approximations of long wavelength and low Reynolds number. All the relations for conservation of momentum, energy and nanoparticles concentration are made dimensionless after introducing suitable relative non-dimensional parameters. The consequent expressions consist of highly non-linear and coupled partial differential equations which are solved analytically with the help of homotopy perturbation method (HPM). The influences of all emerging parameters are imported through presenting the graphs of velocity profile, temperature distribution, nanoparticles concentration, pressure rise and pressure gradient variations. Three-dimensional graphs are also presented for velocity profile. In the end, stream functions are also configured with the help of streamlines which reveal the trapping bolus phenomenon.

Mathematical structure

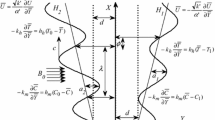
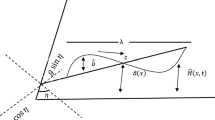
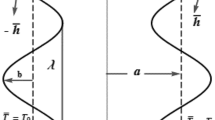
We consider the peristaltic flow of an incompressible Jeffrey fluid with nanoparticles concentration in a cross-section of three-dimensional uniform rectangular channel (Reddy et al. 2005). The flow is produced by the propagation of sinusoidal waves having wavelength λ  travelling along the axial direction of the channel with constant speed c (Fig. 1). The equations for the conservation of mass, momentum, energy and nanoparticles concentration for Jeffrey fluid are described as (Nadeem et al. 2013):

Equation of mass conservation

$$ \hbox{div}\,{\mathbf{V}}=0.$$

(1)

Equation of momentum conservation

$$ \rho_{f}\left( \frac{D{\mathbf{V}}}{Dt}\right) =-{\boldsymbol \nabla}P+\hbox{\rm div} {\mathbf{S+}}\rho_{f}g\alpha_{f}\left( \bar{T}-T_{0}\right) +\rho_{f}g\alpha_{f}\left(\bar{C}-C_{0}\right).$$

(2)

Equation of energy conservation

$$ \rho_{f}c_{f}\left( \frac{D\bar{T}}{Dt}\right) ={\boldsymbol \nabla} \cdot K {\boldsymbol\nabla}\bar{T}+\rho_{p}c_{p}\left( D_{B}\left( {\boldsymbol \nabla}\bar{C}\cdot{\boldsymbol \nabla}\bar{T}\right) +\frac{D_{T}}{T_{0}} \left( {\boldsymbol \nabla}\bar{T}\cdot {\boldsymbol \nabla}\bar{T}\right) \right). $$

(3)

Equation of nanoparticles concentration

$$ \frac{D\bar{C}}{Dt}=D_{B}\boldsymbol{\nabla}^{2}\bar{C}+\frac{D_{T}}{ T_{0}}\boldsymbol{\nabla }^{2}\bar{T}, $$

(4)

where $\mathbf{S}$ represents the constitutive relations for Jeffrey fluid model which is defined as (Kothandapani and Srinivas 2008):

$$ {\mathbf{S}}=\frac{\mu }{1+\lambda_{1}}\left( \overset{\cdot }{\boldsymbol{\gamma}}+\lambda_{2}\overset{\cdot \cdot }{\boldsymbol{\gamma}}\right). $$

(5)

In above expression, μ is the viscosity of the fluid, $\overset{\cdot }{{\varvec{\gamma}}}$ is the symmetric part of velocity gradient and λ₁ is the constant Jeffrey parameter.

The peristaltic waves on the walls are represented as (Reddy et al. 2005)

$$ Z=\pm H(X,t)=\pm a\pm b\cos \left[ \frac{2\pi }{\lambda }\left( X-ct\right) \right], $$

where a and b are the amplitudes of the waves, t is the time and X is the direction of wave propagation.

Formulation of the problem

The walls parallel to XZ-plane remain undisturbed and are not subject to any peristaltic wave motion. We assume that the lateral velocity is zero as there is no change in lateral direction of the duct cross-section. The governing equations for flow velocity $\mathbf{V}=\left( U,0,W\right)$ of the nanofluid in three-dimensional flow problem will have the following form:

$$ \frac{\partial U}{\partial X}+\frac{\partial W}{\partial Z} =0, $$

(6)

$$ \begin{aligned} \rho_{f}\left( \frac{\partial U}{\partial t}+U\frac{\partial U}{\partial X} +W\frac{\partial U}{\partial Z}\right) = -\frac{\partial P}{\partial X}+ \frac{\partial }{\partial X}S_{XX}+\frac{\partial }{\partial Y}S_{XY}+\frac{ \partial }{\partial Z}S_{XZ}\\ &{\mathbf{+}}\rho _{f}g\alpha _{f}\left( \bar{T}-T_{0}\right) +\rho _{f}g\alpha _{f}\left( \bar{C}-C_{0}\right), \end{aligned} $$

(7)

$$ 0=-\frac{\partial P}{\partial Y}+\frac{\partial }{\partial X}S_{YX}+ \frac{\partial }{\partial Y}S_{YY}+\frac{\partial }{\partial Z} S_{YZ}, $$

(8)

$$ \rho _{f}\left( \frac{\partial W}{\partial t}+U\frac{\partial W}{ \partial X}+W\frac{\partial W}{\partial Z}\right) =-\frac{\partial P}{ \partial Z}+\frac{\partial }{\partial X}S_{ZX}+\frac{\partial }{\partial Y} S_{ZY}+\frac{\partial }{\partial Z}S_{ZZ}, $$

(9)

$$ \begin{aligned} \frac{\partial \bar{T}}{\partial t}+U\frac{\partial \bar{T }}{\partial X}+W\frac{\partial \bar{T}}{\partial Z}=\alpha \left( \frac{ \partial ^{2}\bar{T}}{\partial X^{2}}+\frac{\partial ^{2}\bar{T}}{ \partial Y^{2}}+\frac{\partial ^{2}\bar{T}}{\partial Z^{2}}\right) +\tau \left( D_{B}\left( \frac{\partial \bar{C}}{\partial X}\frac{ \partial \bar{T}}{\partial X}+\frac{\partial \bar{C}}{\partial Y} \frac{\partial \bar{T}}{\partial Y}\right. \right. \\ \left. \left. +\frac{\partial \bar{C}}{\partial Z}\frac{ \partial \bar{T}}{\partial Z}\right) +\frac{D_{T}}{T_{0}}\left( \left( \frac{\partial \bar{T}}{\partial X}\right) ^{2}+\left( \frac{\partial \bar{T}}{\partial Y}\right) ^{2}+\left( \frac{\partial \bar{T}}{ \partial Z}\right) ^{2}\right) \right), \end{aligned} $$

(10)

$$ \frac{\partial \bar{C}}{\partial t}+U\frac{\partial \bar{C} }{\partial X}+W\frac{\partial \bar{C}}{\partial Z}=D_{B}\left( \frac{\partial ^{2}\bar{C}}{\partial X^{2}}+\frac{\partial ^{2}\bar{C}}{ \partial Y^{2}}+\frac{\partial ^{2}\bar{C}}{\partial Z^{2}}\right) + \frac{D_{T}}{T_{0}}\left( \frac{\partial ^{2}\bar{T}}{\partial X^{2}}+ \frac{\partial ^{2}\bar{T}}{\partial Y^{2}}+\frac{\partial ^{2} \bar{T}}{\partial Z^{2}}\right),$$

(11)

where $\tau =\left( \rho c\right) _{p}/\left( \rho c\right) _{f}$ is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the base fluid. Let us analyze the flow in a wave frame $\left( x,y,z\right)$ moving with a constant velocity c away from the fixed frame $\left( X,Y,Z\right)$ by the transformation

$$ x=X-ct,\,y=Y,\,z=Z,\,u=U-c,\,w=W,\,p(x,z)=P(X,Z,t),\,T=\bar{T}, C=\bar{C}. $$

(12)

To reduce the number of extra parameters, we define the following non-dimensional quantities:

$$ \begin{aligned} &\bar{x}=\frac{x}{\lambda},\quad \bar{y}=\frac{y}{d},\quad \bar{z}=\frac{z}{a},\quad \bar{t}=\frac{c}{\lambda}t,\quad \bar{u}=\frac{u}{c},\quad \bar{w}=\frac{w}{c\delta},\quad \theta=\frac{T-T_{0}}{T_{1}-T_{0}},\quad \sigma =\frac{C-C_{0}}{ C_{1}-C_{0}},\quad \bar{h}=\frac{H}{a},\quad \beta =\frac{a}{d},\\ &\delta =\frac{a}{\lambda },\quad \phi =\frac{b}{a},\quad B_{r}= \frac{\rho _{f}g\alpha_{f}a^{2}}{\mu c}\left( C_{1}-C_{0}\right),\quad G_{r}=\frac{\rho_{f}g\alpha_{f}a^{2}}{\mu c}\left( T_{1}-T_{0}\right), \quad \alpha =\frac{K}{\left( \rho c\right)_{f}},\quad \bar{p}= \frac{a^{2}p}{\mu c\lambda},\\ &N_{b}=\frac{\tau D_{B}}{\alpha }\left( C_{1}-C_{0}\right) ,\quad N_{t}=\frac{D_{T}}{T_{0}\alpha }\left( T_{1}-T_{0}\right) ,\quad S_{c}= \frac{\mu }{\rho D_{B}},\quad P_{r}=\frac{\mu }{\rho \alpha },\quad \bar{S}=\frac{a}{\mu c}S,\quad Re=\frac{\rho ac}{\mu }. \end{aligned} $$

Therefore, the non-dimensional governing equations (after exempting the bar symbols) for Jeffrey nanofluid in a wave frame will obtain the subsequent form:

$$ \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0, $$

(13)

$$ Re\,\delta \left( u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z}\right) =-\frac{\partial p}{\partial x}+\frac{1}{1+\lambda _{1} }\left( \delta ^{2}\frac{\partial ^{2}u}{\partial x^{2}}+\beta ^{2}\frac{ \partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{\partial z^{2}}\right) +B_{r}\sigma +G_{r}\theta , $$

(14)

$$ 0=\frac{\partial p}{\partial y}, $$

(15)

$$ Re\,\delta \left( u\frac{\partial w}{\partial x}+w\frac{\partial w}{\partial z}\right) =-\frac{\partial p}{\partial z}+\frac{Re\,\delta }{1+\lambda _{1}}\left( \delta ^{2}\frac{\partial ^{2}w}{\partial x^{2}} +\beta ^{2}\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{ \partial z^{2}}\right), $$

(16)

$$ \begin{aligned} Re\,\delta P_{r}\left( u\frac{\partial \theta}{\partial x}+w \frac{\partial \theta }{\partial z}\right)&=\delta ^{2}\frac{\partial ^{2}\theta }{\partial x^{2}}+\beta ^{2}\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}+N_{b}\left( \delta ^{2} \frac{\partial \theta }{\partial x}\frac{\partial \sigma }{\partial x}+\beta ^{2}\frac{\partial \theta }{\partial y}\frac{\partial \sigma }{\partial y} +\right. \left.\frac{\partial \theta }{\partial z}\frac{\partial \sigma}{\partial z}\right)\\ &\quad+N_{t}\left( \delta ^{2}\left( \frac{\partial \theta }{\partial x}\right) ^{2}+\beta ^{2}\left( \frac{\partial \theta }{\partial y} \right) ^{2}+\left( \frac{\partial \theta }{\partial z}\right) ^{2}\right), \end{aligned} $$

(17)

$$Re\,\delta S_{c}\left( u\frac{\partial \sigma }{\partial x}+w \frac{\partial \sigma }{\partial z}\right)=\delta ^{2}\frac{\partial ^{2}\sigma }{\partial x^{2}}+\beta ^{2}\frac{\partial ^{2}\sigma }{\partial y^{2}}+\frac{\partial ^{2}\sigma }{\partial z^{2}}+\frac{N_{t}}{N_{b}}\left( \delta ^{2}\frac{\partial ^{2}\theta }{\partial x^{2}}+\beta ^{2}\frac{ \partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}\right) , $$

(18)

where P _r ,  N _b ,  N _t ,  G _r and B _r represent the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number, respectively. The boundaries of the channel will obtain the dimensionless form as follows:

$$ z=\pm h(x)=\pm 1\pm \phi \cos 2\pi x. $$

(19)

Under the assumption of long wavelength δ ≤ 1 and low Reynolds number $Re\longrightarrow 0$ (Reddy et al. 2005), Eqs. (13)–(18) simplify to the following form:

$$ \left( \beta ^{2}\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{\partial z^{2}}\right) +\left( 1+\lambda _{1}\right) \left( B_{r}\sigma +G_{r}\theta \right)=\left( 1+\lambda _{1}\right) \frac{{\rm d}p}{{\rm d}x} , $$

(20)

$$ \beta ^{2}\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}+N_{b}\left( \beta ^{2}\frac{\partial \theta }{ \partial y}\frac{\partial \sigma }{\partial y}+\frac{\partial \theta }{ \partial z}\frac{\partial \sigma }{\partial z}\right) +N_{t}\left( \beta ^{2}\left( \frac{\partial \theta }{\partial y}\right) ^{2}+\left( \frac{ \partial \theta }{\partial z}\right) ^{2}\right)=0, $$

(21)

$$ \beta^{2}\frac{\partial ^{2}\sigma }{\partial y^{2}}+\frac{\partial ^{2}\sigma }{\partial z^{2}}+\frac{N_{t}}{N_{b}}\left( \beta ^{2}\frac{ \partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}\right) =0. $$

(22)

The corresponding boundary conditions are

$$ u=-1\hbox { at }y=\pm 1,\hbox { }u=-1\hbox { at }z=\pm h\left( x\right) , $$

(23)

$$ \theta =a_{1}\quad\hbox{at}\; y=1,\quad\theta =b_{1}\quad\hbox{at}\; y=-1,\quad\theta =0\quad\hbox{at}\; z=h(x),\quad\theta = 1\quad\hbox{at}\; z=-h(x), $$

(24)

$$ \sigma =a_{2}\quad\hbox{at}\; y=1,\quad\sigma =b_{2}\quad\hbox{at}\; y=-1,\quad\sigma =0\quad\hbox{at}\; z=h(x),\quad\sigma =1\quad\hbox{at}\; z=-h(x). $$

(25)

The expressions for the non-dimensional stream functions can be described as u = ∂ψ /∂z,  w =  − ∂ψ /∂x, where ψ represents the stream function.

Solution of the problem

Solution by homotopy perturbation method

The solutions of the above non-linear partial differential Eqs. (20)–(22) have been calculated by optimized series solution technique. The deformation equations for the problem are defined as (He 2006, 2010; Rafiq et al. 2010; Saadatmandi et al. 2009; Ma et al. 2012)

$$ H\left( v,q\right) =\left( 1-q\right) \pounds \left[ v-\widetilde{v} _{0}\right] +q\left( \pounds \left[ v\right] +\beta ^{2}\frac{\partial ^{2}v }{\partial y^{2}}+\left( 1+\lambda _{1}\right) \left( B_{r}\Upomega +G_{r}\Uptheta -\frac{{\rm d}p}{{\rm d}x}\right) \right) =0, $$

(26)

$$ \begin{aligned} H\left( \Uptheta ,q\right)&=\left( 1-q\right) \pounds \left[ \Uptheta - \widetilde{\theta }_{0}\right]\\ &\quad+q\left( \pounds \left[ \Uptheta \right] +\beta ^{2}\frac{\partial ^{2}\Uptheta }{\partial y^{2}}+N_{b}\left( \beta ^{2}\frac{ \partial \Upomega }{\partial y}\frac{\partial \Uptheta }{\partial y}+\right. \right. \left. \left. \frac{\partial \Upomega }{\partial z}\frac{\partial \Uptheta }{\partial z}\right)+N_{t}\left( \beta ^{2}\left( \frac{\partial \Uptheta }{\partial y}\right) ^{2}+\left( \frac{\partial \Uptheta }{\partial z}\right) ^{2}\right) \right)\\ &=0, \end{aligned} $$

(27)

$$ H\left( \Upomega ,q\right) = \left( 1-q\right) \pounds \left[ \Upomega - \widetilde{\sigma }_{0}\right] +q\left( \pounds \left[ \Upomega \right] +\beta ^{2}\frac{\partial ^{2}\Upomega }{\partial y^{2}}+\frac{N_{t}}{N_{b}}\left( \beta ^{2}\frac{\partial ^{2}\Uptheta }{\partial y^{2}}+\frac{\partial ^{2}\Uptheta }{\partial z^{2}}\right) \right) =0. $$

(28)

Here, q is embedding parameter which has the range 0 ≤ q ≤ 1, under the condition that for q = 0, we get the initial solution and for q = 1, we seek the final solution. Here, £ is the linear operator which is taken here as £ = ∂²/∂z². We choose the following initial guesses

$$ \widetilde{v}_{0}\left( y,z\right) =-1+\left( z^{2}-h^{2}\right) +\frac{1}{ \beta ^{2}}\left( 1-y^{2}\right) , $$

(29)

$$ \widetilde{\theta }_{0}=\beta ^{2}\left( z^{2}-h^{2}\right) +\frac{h-z}{2h}= \widetilde{\sigma }_{0}. $$

(30)

Let us define

$$ v\left( x,y,z\right) =v_{0}+qv_{1}+q^{2}v_{2}+\cdots $$

$$ \Uptheta \left( x,y,z\right) =\Uptheta _{0}+q\Uptheta _{1}+q^{2}\Uptheta _{2}+\cdots $$

(31)

$$ \Upomega \left( x,y,z\right) =\Upomega _{0}+q\Upomega _{1}+q^{2}\Upomega _{2}+\cdots $$

Substituting Eq. (31) into Eqs. (26)–(28) and then comparing the like powers of q, one gets the following problems with the corresponding boundary conditions, i.e.,

For q⁰:

$$ \begin{array}{l} \pounds \left( v_{0}\right) -\pounds \left( \widetilde{u}_{0}\right) =0, \\ v_{0}=-1\,\hbox{at}\; y=\pm 1,\quad v_{0}=-1\,\hbox{at}\; z=\pm h(x), \end{array} $$

(32)

$$ \begin{array}{l} \pounds \left( \Uptheta _{0}\right) -\pounds \left( \widetilde{\theta } _{0}\right) =0, \\ \Uptheta _{0}=a_{1}\,\hbox{at}\; y=1, \quad \Uptheta _{0}=b_{1}\,\hbox{at}\; y=-1,\quad \Uptheta _{0}=0\,\hbox{at}\; z=h(x),\quad \Uptheta _{0}=1\,\hbox{at}\; z=-h(x), \end{array} $$

(33)

$$ \begin{array}{l} \pounds \left( \Upomega_{0}\right) -\pounds \left( \widetilde{\sigma}_{0}\right) =0,\\ \Upomega_{0}=a_{2}\,\hbox{at}\,y=1,\quad \Upomega_{0}=b_{2}\,\hbox{at}\,y=-1,\quad \Upomega_{0}=0\,\hbox{at}\,z=h(x),\quad\Upomega_{0}=1\,\hbox{at}\,z=-h(x). \end{array} $$

(34)

For q:

$$ \begin{array}{l} \frac{\partial ^{2}v_{1}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}v_{0} }{\partial y^{2}}+\frac{\partial ^{2}v_{0}}{\partial z^{2}}+\left( 1+\lambda _{1}\right) \left( B_{r}\Upomega _{0}+G_{r}\Uptheta _{0}-\frac{dp}{dx}\right) =0, \\ \qquad v_{1}=0\quad\hbox{at}\,y=\pm 1,\,v_{1}=0\quad\hbox{at}\,z=\pm h(x), \end{array} $$

(35)

$$ \begin{array}{l} \frac{\partial^{2}\Uptheta _{1}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}\Uptheta _{0}}{\partial y^{2}}+\frac{\partial ^{2}\Uptheta_{0}}{\partial z^{2}}+N_{b}\left( \beta ^{2}\frac{\partial \Upomega _{0}}{\partial y}\frac{ \partial \Uptheta _{0}}{\partial y}+\frac{\partial \Upomega_{0}}{\partial z} \frac{\partial \Uptheta _{0}}{\partial z}\right) +N_{t}\left( \beta ^{2}\left( \frac{\partial \Uptheta_{0}}{\partial y}\right) ^{2}+\left( \frac{\partial \Uptheta_{0}}{\partial z}\right) ^{2}\right) =0, \\ \qquad\qquad\Uptheta_{1}=0\quad\hbox{at}\;y=\pm 1,\quad\Uptheta_{1}=0\quad\hbox{at}\;z=\pm h(x), \end{array} $$

(36)

$$ \begin{array}{l} \frac{\partial ^{2}\Upomega _{1}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}\Upomega _{0}}{\partial y^{2}}+\frac{\partial ^{2}\Upomega _{0}}{\partial z^{2}}+\frac{N_{t}}{N_{b}}\left( \beta ^{2}\frac{\partial ^{2}\Uptheta _{0}}{ \partial y^{2}}+\frac{\partial ^{2}\Uptheta _{0}}{\partial z^{2}}\right) =0, \\ \quad\Upomega_{1}=0\,\hbox{at}\,y=\pm 1,\quad\Upomega_{1}=0\,\hbox{at}\,z=\pm h(x). \end{array} $$

(37)

For q²:

$$ \begin{array}{l} \frac{\partial ^{2}v_{2}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}v_{1} }{\partial y^{2}}+\left( 1+\lambda _{1}\right) \left( B_{r}\Upomega _{1}+G_{r}\Uptheta _{1}\right) =0,\\ \quad v_{2}=0\,\hbox{at}\; y=\pm 1,\quad v_{2}=0\,\hbox{at}\; z=\pm h(x), \end{array} $$

(38)

$$ \begin{aligned} &\frac{\partial ^{2}\Uptheta _{2}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}\Uptheta _{1}}{\partial y^{2}}+N_{b}\left( \beta ^{2}\left( \frac{\partial \Upomega _{0}}{\partial y}\frac{\partial \Uptheta _{1}}{\partial y}+\frac{ \partial \Upomega _{1}}{\partial y}\frac{\partial \Uptheta _{0}}{\partial y} \right) +\frac{\partial \Upomega _{0}}{\partial z}\frac{\partial \Uptheta _{1}}{ \partial z}+\left. \frac{\partial \Upomega _{1}}{\partial z}\frac{\partial \Uptheta _{0}}{\partial z}\right) \right.\\ &\quad\left. +2N_{t}\left( \beta ^{2}\frac{\partial \Uptheta _{0}}{\partial y} \frac{\partial \Uptheta _{1}}{\partial y}+\frac{\partial \Upomega _{0}}{\partial z}\frac{\partial \Upomega _{1}}{\partial z}\right) \right) =0,\\ \Uptheta_{2}=&0\,\hbox{at}\,y=\pm 1,\quad \Uptheta _{2}=0\,\hbox{at}\,z=\pm h(x), \end{aligned} $$

(39)

$$ \begin{array}{l} \frac{\partial ^{2}\Upomega _{2}}{\partial z^{2}}+\beta ^{2}\frac{\partial ^{2}\Upomega _{1}}{\partial y^{2}}+\frac{N_{t}}{N_{b}}\left( \beta ^{2}\frac{ \partial ^{2}\Uptheta _{1}}{\partial y^{2}}+\frac{\partial ^{2}\Uptheta _{1}}{ \partial z^{2}}\right) =0, \\ \Upomega_{2}=0\;\hbox{at}\;y=\pm 1,\quad\Upomega_{2}=0\;\hbox{at}\;z=\pm h(x). \end{array} $$

(40)

The resulting series solutions after three iterations are determined using Eq. (31) as (when $q\longrightarrow 1)$ and are evaluated as

$$ \begin{aligned} u\left( x,y,z\right) &=\frac{1}{1440h^{2}N_{b}\beta ^{2}}\left( \vphantom{\left( 4+\frac{dp}{dx}+\frac{dp}{dx }\lambda _{1}\right)}15G_{r}N_{b}(N_{b}+N_{t})z^{4}\right. \beta ^{2}(1+\lambda _{1})-56G_{r}h^{5}N_{b}(N_{b}+N_{t})z\beta ^{4}(1+\lambda _{1})\\ &\quad+224G_{r}h^{8}N_{b}(N_{b}+N_{t})\beta ^{6}(1+\lambda _{1})+24hN_{b}z^{3}\beta ^{2}\left(5(B_{r}+G_{r})-G_{r}(N_{b}+N_{t})z^{2}\beta ^{2}\right)(1+\lambda _{1})\\ &\quad+40h^{3}N_{b}z\beta ^{2}\left( -3(B_{r}+G_{r})+2G_{r}(N_{b}+N_{t})z^{2}\beta ^{2}\right) (1+\lambda _{1})-120h^{6}\beta ^{4}\left(5(B_{r}+G_{r})N_{b}\right.\\ &\quad-5B_{r}N_{t}+\left. 2G_{r}N_{b}(N_{b}+N_{t})z^{2}\beta ^{2}\right) (1+\lambda _{1})+15h^{4}\beta ^{2}\left( \vphantom{\left( 4+\frac{dp}{dx}+\frac{dp}{dx }\lambda _{1}\right)}5G_{r}N_{b}^{2}(1+\lambda _{1})\right.\\ &\quad-48B_{r}N_{t}z^{2}\beta ^{2}(1+\lambda _{1})+N_{b}\left( \vphantom{\left( 4+\frac{dp}{dx}+\frac{dp}{dx }\lambda _{1}\right)}24B_{r}\right. (1+2z^{2}\beta ^{2})(1+\lambda _{1})+G_{r}(24+5N_{t}+48z^{2}\beta ^{2})(1+\lambda _{1})\\ &\quad-48\left. \left. \left( 4+\frac{dp}{dx}+\frac{dp}{dx}\lambda _{1}\right) \right) \right) +2h^{2}\left( \vphantom{\left( 4+\frac{dp}{dx}+\frac{dp}{dx }\lambda _{1}\right)}60B_{r}N_{t}z^{4}\beta ^{4}(1+\lambda _{1})+G_{r}N_{b}^{2}z^{2}\beta ^{2}(-45+8z^{4}\beta ^{4})(1+\lambda _{1})\right.\\ &\quad-N_{b}(-720+720y^{2}+60(B_{r}+G_{r})(z^{4})(\beta ^{4})(1+\lambda _{1})-8G_{r}N_{t}z^{6}\beta ^{6}(1+\lambda _{1})\\ &\quad+45\beta ^{2}(16+z^{2}(4B_{r}(1+\lambda _{1})+G_{r}(4+N_{t})(1+\lambda _{1})-8\left. \left. \left. \left. \left( 4+\frac{dp}{dx}+\frac{dp}{dx }\lambda _{1}\right) \right) \right) \right) \right), \end{aligned} $$

(41)

$$ \begin{aligned} \theta \left( x,y,z\right) =&\frac{1}{720h^{3}}\left( 15\left( 6h^{3}(4+N_{b}+N_{t})\right. \right. +h^{2}\left( -24+(N_{b}+N_{t})(N_{b}+2N_{t})\right) z-6h\left( N_{b}+N_{t}\right) z^{2}\\ &\left. -(N_{b}+N_{t})(N_{b}+2N_{t})z^{3}\right) -60h(h-z)(h+z)\left( 12h^{2}+2h(2N_{b}+N_{t})z\right. +(N_{b}+N_{t})\\ &\left. (N_{b}+2N_{t})z^{2}\right) \beta ^{2}+16h^{2}(h-z)(h+z)\left( 15h^{3}N_{b}\right. +h^{2}(N_{b}+N_{t})(N_{b}+2N_{t})z+15h\\ &N_{b}z^{2}+6\left. (N_{b}+N_{t})(N_{b}+2N_{t})z^{3}\right) \beta ^{4}-64h^{3}(N_{b}+N_{t})(N_{b}+2N_{t})\left. \left( h^{6}-z^{6}\right) \beta ^{6}\right) , \end{aligned} $$

(42)

$$ \begin{aligned} \sigma \left( x,y,z\right) =&\frac{1}{24h^{2}N_{b}}\left( 3N_{t}(N_{b}+N_{t})\right. z^{2}-24h^{4}(N_{b}-N_{t})\beta ^{2}+8h^{3}N_{t}(N_{b}+N_{t})z\beta ^{2}-8h^{6}N_{t}\\ &(N_{b}+N_{t})\beta ^{4}-4h\left( 2N_{t}^{2}z^{3}\beta ^{2}\right. +N_{b}z\left. \left( 3+2N_{t}z^{2}\beta ^{2}\right) \right) +h^{2}\left( N_{t}\left( -3N_{t}-24z^{2}\beta ^{2}+\right. \right.\\ &\left. 8N_{t}z^{4}\beta ^{4}\right) +N_{b}\left. \left. \left( 12-3N_{t}+24z^{2}\beta ^{2}+8N_{t}z^{4}\beta ^{4}\right) \right) \right) . \end{aligned} $$

(43)

The volumetric flow rate q is calculated as

$$ \left. q=\int\limits_{0}^{h\left( x\right) }\int\limits_{0}^{1}u\left( x,y,z\right) {\rm d}y{\rm d}z.\right. $$

(44)

The average volume flow rate over one period $\left( T=\frac{\lambda }{c}\right)$ of the peristaltic wave is defined as

$$ Q=\int\limits_{0}^{h\left( x\right) }\int\limits_{0}^{1}\left( u\left( x,y,z\right) +1\right) {\rm d}y{\rm d}z=q+h\left( x\right). $$

(45)

The pressure gradient dp/dx is obtained after solving Eqs. (44) and (45) and is found as

$$ \begin{aligned} \frac{{\rm d}p}{{\rm d}x}=&\frac{1}{1680h^{3}(1+\lambda _{1})}\left( -5040Q+\frac{ (3360h)}{\beta ^{2}}\right. +512G_{r}h^{7}\left( N_{b}+N_{t}\right) \beta ^{4}\left( 1+\lambda _{1}\right)\\ &+21h^{3}(-320+35B_{r}(1+\lambda _{1})+G_{r}(35+8N_{b}+8N_{t})(1+\lambda _{1}))\\ &-\left. \frac{\left( 42h^{5}\left( 32B_{r}(N_{b}-N_{t})\right. \right. +G_{r}N_{b}\left. (32+N_{b}+N_{t})\right) \left. \beta ^{2}(1+\lambda _{1})\right) }{N_{b}}\right) . \end{aligned} $$

(46)

The pressure rise $\Updelta p$ is evaluated by numerically integrating the pressure gradient dp/dx over one wavelength, i.e.,

$$ \Updelta p=\int\limits_{0}^{1}\frac{{\rm d}p}{{\rm d}x}{\rm d}x. $$

(47)

Results and discussions

The analytical solutions are obtained for the equations of momentum, energy and nanoparticles concentration with the help of well-known homotopy perturbation technique up to third order deformation. All the obtained solutions are discussed graphically under the variations of various pertinent parameters in the present section. The effects of lateral walls (aspect ratio β), Jeffrey fluid parameter λ₁, average volume flow rate Q, amplitude ratio ϕ, the Brownian motion parameter N _b , the thermophoresis parameter N _t , local temperature Grashof number G _r and local nanoparticle Grashof number B _r on the profiles of velocity u, temperature θ, nanoparticles concentration σ, pressure gradient dp/dx and pressure rise $\Updelta p$ are presented by drawing graphs for two and three dimensions. The trapping bolus phenomenon is also incorporated through sketching graphs of streamlines for various physical parameters.

Figure 2 contains the behavior of velocity profile under the variation of β and Jeffrey fluid parameter λ₁. It is mentioned here that velocity profile is rising up with the increasing effects of both the parameters and attains its maximum height at z = 0. This reveals the fact that when we increase the magnitude of lateral walls either by increasing vertical height a or by decreasing the horizantal distance d, the fluid velocity starts increasing and tends to be constant at the peristaltic walls $\pm h\left( x\right)$ as specified by the boundary conditions. One can observe the variation of B _r and G _r for the velocity distribution versus vertical height z in Fig. 3. One can depict here that velocity is varying directly with the corresponding change in both the parameters. It is also measured that when value of z increases, velocity also increases and reaches its peak at z = 0 after that it starts declining and becomes stable at the boundary to meet the physical boundary conditions. From Figs. 4 and 5, we derive the consequence that velocity profile gives inverse behavior with the variation of N _b but similar attitude is observed for N _t and Q.

Fig. 1

Schematic diagram for peristaltic flow in a rectangular duct

Fig. 2

Velocity profile u for different values of β and λ₁ for fixed G _r  = 1, B _r  = 0.6,  N _t  = 0.9,  N _b  = 0.5,  Q = 0.2,  ϕ = 0.3,  x = 0,  y = 1, a for two-dimensional, b for three-dimensional

Fig. 3

Velocity profile u for different values of B _r and G _r for fixed β = 1.2,  λ₁ = 0.6,  N _t  = 0.9,  N _b  = 0.5,  Q = 0.2,  ϕ = 0.2,  x = 0,  y = 1,  a for two-dimensional, b

Fig. 4

Velocity profile u for different values of N _b and N _t for fixed G _r  = 1,  B _r  = 0.2, β = 1.2, λ₁ = 0.6,  Q = 0.2,  ϕ = 0.2,  x = 0,  y = 1, a for two-dimensional, b for three-dimensional

Fig. 5

Velocity profile u for different values of Q for fixed G _r  = 1,  B _r  = 0.2,  N _t  = 0.9,  N _b  = 0.5, β = 1.2, λ₁ = 0.6,  ϕ = 0.2,  x = 0,  y = 1, a for two-dimensional, b for three-dimensional

Figure 6 implies the temperature distribution drawn along the variation of lateral walls $\left( \beta \right)$ with keeping other parameters constant. It is to be noted here that temperature curve gives linear behavior at β = 0.1 but after then for large values of lateral walls, it starts bending and gets its maximum curvature near z =  − 0.1 and vanishes at $z=h\left( x\right)$ to meet the physical aspects at the walls. It is observed from Fig. 7 that temperature distribution is a decreasing function of N _t and N _b in the region $z\in \left[ -1.5,0\right)$, but in the rest of the domain, it shows opposite variation, i.e., curves start increasing but with a small extent as compared with their decreasing ratio and look like almost invariant for the small values of both the parameters in the region z ≥ 0. The influence of lateral walls on nanoparticles concentration can be measured from Fig. 8. It is noticed that the behavior of concentration profile is almost similar to that of temperature profile with the variation of β. However, it is depicted that nanoparticles concentration is directly proportional to the variation of N _b but inversely related to N _t (see Fig. 9). It is also an interesting fact that can be noted here that as one moves from $-h\left( x\right)$ to 0, the curves are declining, but as we move forward, those start to rise and get stable at $h\left( x\right).$

Fig. 6

Temperature profile θ for different values of β for fixed N _t  = 0.1,  N _b  = 0.1,  ϕ = 0.2,  x = 0,  y = 1

Fig. 7

Temperature profile θ for different values of N _b and N _t for fixed β = 0.3,  ϕ = 0.5,  x = 0,  y = 1

Fig. 8

Nanoparticles concentration profile σ for different values of β for fixed N _t  = 0.1,  N _b  = 0.1,  ϕ = 0.2,  x = 0,  y = 1

Fig. 9

Nanoparticles concentartion profile σ for different values of N _b and N _t for fixed β = 0.5,  ϕ = 0.1,  x = 0,  y = 1

Figure 10 is constructed to see the effects of lateral walls and amplitude ratio on the pressure rise distribution. It is concluded that peristaltic pumping region $\left( \Updelta p>0,Q>0\right)$ lies between 0 and 0.5, free pumping $\left( \Updelta p=0\right)$ occurs near Q = 0.2, retrograde pumping $\left( \Updelta p>0,Q<0\right)$ is $Q\in \left[ -1,0\right]$ and reverse pumping area $\left( \Updelta p<0,Q>0\right)$ is 0.5 ≤ Q ≤ 2. It is noted here that in peristaltic and retrograde pumping, $\Updelta p$ is increasing with increase in amplitude ratio but in reverse pumping (copumping), it gives inverse variation and for the variation of aspect ratio, it also decreases. It is also observed here that pressure rise curves are strictly decreasing with the increase in the numerical values of the flow rate Q. From Fig. 11, it is depicted that with the increase in Jeffrey fluid parameter λ₁, pressure rise curves are diminishing in peristaltic and retrograde pumping regions while they behave inversely in the reverse pumping. It is also seen that peristaltic pumping is reduced with the greater values of B _r . It is observed from Fig. 12 that peristaltic pumping rate increases with the variation of G _r . Figure 13 reveals that pressure rise profile declines in peristaltic pumping and retrograde pumping with λ₁ but rises up in the reverse pumping side. It is also concluded that pumping rate increases to maintain the flow with the increase in N _t .

Fig. 10

Variation of pressure rise $\Updelta p$ with β and ϕ at N _t  = 0.1,  N _b  = 0.1,  G _r  = 0.2, λ₁ = 0.5,  B _r  = 0.2

Fig. 11

Variation of pressure rise $\Updelta p$ with B _r and λ₁ at N _t  = 0.1,  N _b  = 0.1,  G _r  = 0.2, ϕ = 0.2, β = 0.8

Fig. 12

Variation of pressure rise $\Updelta p$ with G _r and ϕ at N _t  = 0.1,  N _b  = 0.1,  B _r  = 0.6, λ₁ = 0.8, β = 0.9

Fig. 13

Variation of pressure rise $\Updelta p$ with N _t and λ₁ at G _r  = 0.2, N _b  = 0.1,  B _r  = 0.1,  ϕ = 0.2,  β = 0.8

Pressure gradient curves dp/dx are sketched in Fig. 14 to see the variation of lateral walls and flow rate. It is shown here that pressure gradient is a decreasing function of both the lateral walls and flow rate, and much pressure change is observed at the centre which implies that much pressure gradient is needed at the centre to follow the same flow as compared with the corners where flow passes more easily without imposition of much pressure gradient. It is also seen that for $x\in \left( 0,0.5\right) ,$ the pressure gradient profile is increasing but after that it starts decreasing with the same ratio and becomes minimum at x = 1. It can be measured from Fig. 15 that as we increase the values of G _r and B _r , pressure gradient gets decreased in the regions $x\in \left[ 0,0.3\right] \cup \left[ 0.7,1\right]$ while inversed in the middle of the domain. It is also noted that pressure gradient variation is greater at the corner regions as compared with the central area which shows that more pressure is required at the left and right sides to maintain the flow. Figure 16 shows totally opposite picture for for amplitude ratio and fluid parameter with that of seen in the previous graph for G _r and B _r . However, in the current figure, almost similar variation is seen throughout the domain. It is derived from Fig. 17 that pressure gradient is varying directly with N _b and N _t and pressure change remains continuous and positive throughout for N _b and N _t .

Fig. 14

Variation of pressure gradient dp/dx with β and Q at N _t  = 0.1,  N _b  = 0.5,  G _r  = 0.2, λ₁ = 3,  ϕ = 0.5,  B _r  = 0.2

Fig. 15

Variation of pressure gradient dp/dx with B _r and G _r at N _t  = 0.1,  N _b  = 0.5, β = 0.8, λ₁ = 3,  ϕ = 0.4,  Q = 0.1

Fig. 16

Variation of pressure gradient dp/dx with λ₁ and ϕ at N _t  = 0.1,  N _b  = 0.5,  G _r  = 0.5,  β = 0.8,  Q = 0.1,  B _r  = 0.3

Fig. 17

Variation of pressure gradient dp/dx with N _b and N _t at λ₁ = 0.3,  ϕ = 0.05,  G _r  = 2,  β = 0.3,  Q = 0.5,  B _r  = 0.2

Trapping bolus phenomenon reads variation of travelling of circulating bolus covered by streamlines as the flow progresses. Figure 18 contains the streamlines for the variation of G _r and found that for G _r  = 0.8, a very small bolus is observed in the upper half while a relatively larger bolus is seen at the lower half, but as we give rise to value of G _r  = 1, the upper bolus is expanded and the lower one is shrinked and after then the upper one again starts contracting and the lower one expanding. It is also noted that as the magnitude of G _r varies, the bolus is getting more streamlines around it. It is observed from Fig. 19 that for increasing fluid parameter λ₁, the bolus becomes larger and more streamlines are obtained in its surroundings. Figure 20 gives the variation of streamlines for the increasing effects of N _b and evaluates that the bolus is contracted at N _b  = 0.2 for upper half but expanded for the lower side but when we approach at N _b  = 0.3, inverse variation is calculated for both lower and upper half. It is also to be noted that streamlines are decreasing in numbers as we increase N _b .

Fig. 18

Stream lines for different values of G _r , a for G _r  = 0.8, b for G _r  = 1, c for G _r  = 1.2. The other parameters are B _r  = 0.2,  β = 1.5,  N _t  = 0.5,  λ₁ = 0.6,  N _b  = 0.5,  ϕ = 0.15,  Q = 2,  y = 1

Fig. 19

Stream lines for different values of λ₁, a for λ₁ = 0.2, b for λ₁ = 0.6, c for λ₁ = 1. The other parameters are B _r  = 0.2,  G _r  = 1,  β = 1.5,  N _t  = 0.5,  N _b  = 0.5,  ϕ = 0.15,  Q = 1,  y = 1

Fig. 20

Stream lines for different values of N _b ,  (a) for N _b  = 0.1, (b) for N _b  = 0.2, (c) for N _b  = 0.3. The other parameters are B _r  = 0.2,  G _r  = 1,  β = 1.5,  N _t  = 0.5, λ₁ = 0.6,  ϕ = 0.15,  Q = 1,  y = 1

Concluding remarks

Peristaltic flow of a non-Newtonian (Jeffrey) nanofluid is considered in a cross-section of rectangular duct to describe the mathematical results under convective heat transfer phenomenon and nanoparticles concentration. All the governing equations are modeled under the approximations of long wavelength and low Reynolds number. The flow is measured in a wave frame of reference moving with a constant velocity c along axial direction of the channel. Analytical results are obtained using homotopy perturbation method and the aspects of all physical parameters occurring in the phenomenon are discussed manually. The resulting points obtained from the above observations are stated as:

• 1. It is observed that velocity profile is an increasing function of λ₁,  β, B _r ,  G _r ,  N _t and Q but decreasing function of N _b both for two- and three-dimensional analysis.

• 2. Temperature distribution is varying inversely with β, also the above discussion reveals that temperature curves are diminishing with N _b and N _t in left half while rising in the right part of the z domain.

• 3. It is concluded that nanoparticles concentration reveals opposite relation with lateral walls effects and N _t but curves are rising up with increase in N _b .

• 4. One can extract from above analysis that peristaltic pumping rate increases with the increase in ϕ, G _r and N _t , however, it reduces for β, λ₁,  B _r and N _b .

• 5. It is mentioned that pressure gradient profile shows reverse variation with β, Q,  λ₁ and ϕ and direct relation with N _b and N _t .

• 6. It is also noted that change in pressure is positive with B _r , G _r ,  λ₁ and ϕ in middle part of the channel while negative in the corner sides.

• 7. We can declare that trapping bolus is expanding with G _r and λ₁ in the upper half while shrinking in the lower part of the flow domain while reverse attitude is appeared with N _b .