The mathematical analysis for peristaltic flow of nano fluid in a curved channel with compliant walls

Abstract

In the present paper, we have investigated the peristaltic flow of nano fluid in a curved channel with compliant walls. The governing equations of nano fluid model for curved channel are derived including the effects of curvature. The highly nonlinear partial differential equations are simplified using the long wave length and low Reynolds number assumptions. The reduced nonlinear partial differential equation is solved analytically with the help of homotopy perturbation method. The physical features of pertinent parameters have been discussed by plotting the graphs of pressure rise, velocity, temperature, nano particle volume fraction and stream functions.

Introduction

The topic of peristalsis is highly important in modern applied mathematics, engineering and physiological world. This is because of its many applications in real life such as swallowing food through the oesophagus, chyme motion in the gastrointestinal tract, in the vasomotion of small blood vessels such as venules, capillaries and arterioles, urine transport from kidney to bladder, in sanitary fluid transport, transport of corrosive fluids, a toxic liquid transport in the nuclear industry, etc,. Many researchers have discussed the peristaltic flows of viscous and non-Newtonian fluids theoretically and experimentally (Nadeem and Hameed 2007; Nadeem and Akbar 2009, 2010; Nadeem et al. 2010; Nadeem and Akram 2010a; Mekheimer 2008; Mekheimer and Abd elmabound 2008, 2011; Tripathi et al. 2010; Tripathi and Chhabra 1996). In these days, researchers have focussed their attention on the study of the nano fluid for different flow geometries. Recently, Nadeem and Akram (2010b) have considered the peristaltic flow of a nano fluid model in an asymmetric channel. In another study, Nadeem et al. (2012) have discussed the peristaltic flow of a nano fluid in an inclined asymmetric channel with partial slip and heat transfer. However, only few papers are available in literature, which discuss the peristaltic flow in a curved channel. Sato et al. (2000) have initiated the peristaltic flow in a curved channel. In their work Sato et al. concluded that the curvature parameter affects the fluid flow to a great extent. This effect is graphically shown in streamlines plots for different values of curvature parameter k. They concluded that the size of the bolus near the outer wall increases with increasing values of k, while the size of the bolus near the inner wall remains unaltered. However, when large values of Wessingber number W_e are taken in to the account the bolus near the inner wall disappears. Very recently, Hayat et al. (2011) have examined the peristaltic flow of viscous fluid in a curved channel with compliant walls. In this paper Hayat et al. concluded that the velocity decreases near the walls and increases near the centre of the channel when the compliant wall parameters are increased. Moreover, the curvature parameter effects are plotted for streamlines and size of the bolus grows with increase in curvature parameter.

The peristaltic flow of nano fluid model in curved channel is still not detonated. Therefore, in the present investigation we have highlighted the peristaltic flow of nano fluid in a curved symmetric channel. The governing equations of two-dimensional nano fluid in a curved channel including the effects of curvature are modelled. After the non-dimensionalization and using assumptions of the long wave length and low Reynolds number approximation, the reduced highly nonlinear partial differential equation is solved analytically with the help of homotopy perturbation method. At the end the physical phenomena is discussed by plotting graphs.

Mathematical formulation

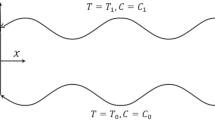
Consider a two-dimensional flow of an incompressible nano fluid in a curved channel of uniform thickness 2a. The channel walls are flexible and also considered as compliant on which small amplitude of the travelling waves are imposed. Defining ($\bar{N}, \bar{S}, \bar{Z}$) as the coordinates in the cross stream, down stream and vertical directions, respectively, and R* as the radius of curvature. The flow in the channel is induced by sinusoidal waves of small amplitude b traveling along the flexible walls of the channel. The walls of the channel are considered as follows:

$$ \bar{N} =\eta =a+b\sin \left[ \frac{2\pi }{\lambda }\left( \bar{S }-c\bar{t}\right) \right] ,\hbox { \quad upper wall} $$

(1)

$$ \bar{N} =-\eta =-a-b\sin \left[ \frac{2\pi }{\lambda }\left( \bar{S}-c\bar{t}\right) \right] .\hbox { \quad lower wall} $$

(2)

In above equations c is the wave speed and λ denotes the wave length. Let $\bar{V}$ and $\bar{U}$ denote the velocity components in the cross stream and down stream directions, respectively. The governing equations of motion, energy and nano particle for curved channel are described as (Wang and Mujumdar 2007; Polidori et al. 2007)

$$ \frac{R^{\ast }}{\bar{N}+R^{\ast }}\frac{\partial }{\partial \bar{N }}\left( \frac{\left( \bar{N}+R^{\ast }\right) }{R^{\ast }}\bar{V} \right) +\frac{R^{\ast }}{\bar{N}+R^{\ast }}\frac{\partial \bar{U} }{\partial \bar{S}} =0, $$

(3)

$$ \begin{aligned} \rho _{\rm{f}}\left( \frac{\partial\bar{V}}{\partial \bar{t}}+ \bar{V}\frac{\partial\bar{V}}{\partial \bar{N}}+\frac{ R^{\ast}\bar{U}}{\bar{N}+R^{\ast }}\frac{\partial \bar{V}}{ \partial\bar{S}}-\frac{\bar{U}^{2}}{\bar{N}+R^{\ast }} \right) &=-\frac{\partial \bar{P}}{\partial \bar{N}}+\frac{2\mu R^{\ast}}{\bar{N}+R^{\ast }}\frac{\partial }{\partial \bar{N}} \left(\left( \bar{N}+R^{\ast }\right) \frac{\partial \bar{V}}{ \partial\bar{N}}\right)\\ &\quad+\frac{\mu R^{\ast }}{\bar{N}+R^{\ast}}\frac{\partial }{\partial \bar{S}}\left( \frac{R^{\ast}}{\bar{N}+R^{\ast }}\frac{\partial \bar{V}}{\partial\bar{S}}+\frac{\partial \bar{U}}{\partial\bar{N}}-\frac{\bar{U}}{\bar{N}+R^{\ast }}\right)\\&\quad-\frac{2\mu }{\bar{N}+R^{\ast }}\left( \frac{R^{\ast}}{\bar{N} +R^{\ast }}\frac{\partial \bar{U}}{\partial\bar{S}}+\frac{ \bar{V}}{\bar{N}+R^{\ast }}\right), \end{aligned}$$

(4)

$$ \begin{aligned} \rho_{\rm{f}}\left( \frac{\partial\bar{U}}{\partial \bar{t}}+ \bar{V}\frac{\partial\bar{U}}{\partial \bar{N}}+\frac{ R^{\ast}\bar{U}}{\bar{N}+R^{\ast }}\frac{\partial \bar{U}}{ \partial\bar{S}}+\frac{\bar{U}\bar{V}}{\bar{N}+R^{\ast } }\right)&=-\frac{R^{\ast }}{\bar{N}+R^{\ast }}\frac{\partial\bar{P}}{\partial \bar{S}}+\frac{\mu }{\bar{N}+R^{\ast }}\frac{\partial }{\partial \bar{N}}\left[ \left( \bar{N}+R^{\ast}\right) \left( \frac{R^{\ast }}{\bar{N}+R^{\ast }}\frac{\partial\bar{V }}{\partial \bar{S}}+\frac{\partial \bar{U}}{\partial\bar{N}} -\frac{\bar{U}}{\bar{N}+R^{\ast }}\right) \right]\\&\quad+\frac{2\mu R^{\ast }}{\bar{N}+R^{\ast }}\frac{\partial}{\partial \bar{S}}\left( \frac{R^{\ast }}{\bar{N}+R^{\ast}}\frac{\partial \bar{V}}{\partial\bar{S}}+\frac{\bar{V}}{\bar{N}+R^{\ast }} \right)\\&\quad+\rho g\alpha \left( \bar{T}-T_{0}\right) +\rho g\alpha\left( \bar{C}-C_{0}\right), \end{aligned} $$

(5)

$$ \left( \rho_ {\rm{c}}\right) _{\rm{f}}\frac{{\rm{d}}\bar{T}}{{\rm{d}}\bar{t}} =\kappa \nabla ^{2}\bar{T}+\left( \rho_ {\rm{c}}\right) _{\rm{p}}\left[ D_{\rm{B}}\nabla \bar{C}\cdot \nabla \bar{T}+\frac{D_{\rm{T}}}{T_{0}}\nabla \bar{T} \cdot \nabla \bar{T}\right], $$

(6)

$$ \frac{{\rm{d}}\bar{C}}{{\rm{d}}\bar{t}} =D_{\rm{B}}\nabla ^{2}\bar{C}+\frac{ D_{\rm{T}}}{T_{0}}\nabla ^{2}\bar{T}. $$

(7)

The corresponding boundary conditions for asymmetric channel having compliant walls are defined as

$$ \bar{U} =0\hbox { at }\bar{S}=\pm \eta =\pm \left[ a+b\sin \left( \frac{2\pi }{\lambda }\left( \bar{S}-c\bar{t}\right) \right) \right], $$

(8)

$$ \begin{aligned} \frac{R^{\ast }}{\bar{S}+R^{\ast }}\frac{\partial }{\partial \bar{S }}L\left( \eta \right) = &\frac{R^{\ast }}{\bar{S}+R^{\ast }}\frac{ \partial \bar{P}}{\partial \bar{S}}=\frac{\mu }{\bar{S} +R^{\ast }}\frac{\partial }{\partial \bar{S}}\left[ \left( \bar{S} +R^{\ast }\right) \left( \frac{R^{\ast }}{\bar{S}+R^{\ast }}\frac{ \partial \bar{V}}{\partial \bar{N}}+\frac{\partial \bar{U}}{ \partial \bar{S}}-\frac{\bar{U}}{\bar{S}+R^{\ast }}\right) \right]\\ &\quad+\frac{2\mu R^{\ast }}{\bar{S}+R^{\ast }}\frac{\partial }{\partial \bar{N}}\left( \frac{R^{\ast }}{\bar{S}+R^{\ast }}\frac{\partial \bar{V}}{\partial \bar{N}}+\frac{\partial \bar{U}}{\partial \bar{S}}-\frac{\bar{U}}{\bar{S}+R^{\ast }}\right)\\ &\left.\quad -\rho _{\rm{f}}\left( \frac{\partial }{\partial t}+\bar{V}\frac{ \partial \bar{U}}{\partial \bar{S}}+\frac{R^{\ast }\bar{U}}{ \bar{S}+R^{\ast }}\frac{\partial \bar{U}}{\partial \bar{N}}+ \frac{\bar{U}\bar{V}}{\bar{S}+R^{\ast }}\right) \hbox { at } \bar{S}=\pm \eta ,\right. \end{aligned} $$

(9)

$$ \bar{T} =T_{0},\quad\bar{C}=C_{0}\hbox { on }\bar{N}=-\eta , $$

(10)

$$ \bar{T} =T_{1},\quad\bar{C}=C_{1}\hbox { on }\bar{N}=\eta. $$

(11)

Here $\rho _{\rm{f}},\mu ,( \rho_ {\rm{c}}) _{\rm{f}},( \rho_ {\rm{c}}) _{\rm{p}},\kappa ,D_{\rm{B}}$ and D_T are the fluid density, dynamic viscosity, heat capacity of the fluid, effective heat capacity of the nano particle material, Thermal conductivity, Brownian diffusion coefficient and thermophoretic diffusion coefficient, respectively. Moreover,

$$ L=-\sigma \frac{\partial ^{2}}{\partial \bar{S}^{2}}+m\frac{\partial ^{2}}{\partial t^{2}}+C\frac{\partial }{\partial t}, $$

(12)

where σ is the longitudinal tension per unit width, m is the mass per unit area and C is the coefficient of viscous damping.

Introducing the following non dimensional variables and velocity stream function relation

$$ \begin{aligned} n =&\frac{\bar{N}}{\lambda },s=\frac{\bar{S}}{a},u=\frac{ \bar{U}}{c},v=\frac{\bar{V}}{c},\psi =\frac{\bar{\psi }}{ca} ,k=\frac{R^{\ast }}{a},\hbox{Re}=\frac{\rho _{\rm{f}}ca}{\mu },\\ \delta =&\frac{a}{\lambda },p=\frac{a^{2}\bar{P}}{c\mu \lambda },t= \frac{c\bar{t}}{\lambda },\theta =\frac{\bar{T}-T_{0}}{T_{1}-T_{0}} ,\sigma =\frac{\bar{C}-C_{0}}{C_{1}-C_{0}},G_{\rm{r}}=\frac{g\alpha a^{2}\left( T_{1}-T_{0}\right) }{\nu c},\epsilon =\frac{b}{a},\\ E_{1} =&-\frac{\sigma a^{3}}{\lambda ^{3}\mu c},E_{2}=\frac{mca^{3}}{ \lambda ^{3}\mu },E_{3}=\frac{Ca^{3}}{\lambda ^{2}\mu },B_{\rm{r}}=\frac{g\alpha a^{2}\left( C_{1}-C_{0}\right) }{\nu c},\alpha =\frac{\kappa }{\left( \rho_ {\rm{c}}\right)_{\rm{f}}},\\ N_{\rm{b}} =&\frac{\left( \rho_ {\rm{c}}\right) _{\rm{p}}D_{\rm{B}}C_{0}}{\alpha \left( \rho_ {\rm{c}}\right) _{\rm{f}}},N_{\rm{t}}=\frac{\left( \rho_ {\rm{c}}\right) _{\rm{p}}D_{\rm{T}}T_{0}}{\alpha \left( \rho_ {\rm{c}}\right) _{\rm{f}}},u=-\frac{\partial \psi }{\partial r},v=\delta \frac{k}{r+k}\frac{\partial \psi }{\partial x},\\ \end{aligned} $$

Equation (3) is identically satisfied and Eqs. (4)–(11) under long wavelength and low Reynolds number approximations are expressed in the following dimensionless form:

$$ \frac{\partial p}{\partial n}=0, $$

(13)

$$ \left( \frac{k}{n+k}\right) \frac{\partial p}{\partial s}=-\frac{1}{n+k} \frac{\partial }{\partial n}\left[ \psi _{nn}+\frac{\left( 1-\psi _{n}\right) }{n+k}\right] +G_{\rm{r}}\theta +B_{\rm{r}}\sigma, $$

(14)

$$ \frac{\partial ^{2}\theta }{\partial n^{2}}+\frac{1}{n+k}\frac{\partial \theta }{\partial n}+\left[ N_{\rm{b}}\frac{\partial \sigma }{\partial n}\frac{ \partial \theta }{\partial n}+N_{\rm{t}}\left( \frac{\partial \theta }{\partial n} \right) ^{2}\right] =0, $$

(15)

$$ \frac{\partial ^{2}\sigma }{\partial n^{2}}+\frac{1}{n+k}\frac{\partial \sigma }{\partial n}+\frac{N_{\rm{t}}}{N_{\rm{b}}}\left[ \frac{\partial ^{2}\theta }{ \partial n^{2}}+\frac{1}{n+k}\frac{\partial \theta }{\partial n}\right] =0, $$

(16)

$$ \psi _{n}=0\hbox { at }n=\pm \eta =\pm \left[ 1+\epsilon \sin 2\pi \left( s-t\right) \right] , $$

(17)

$$ -\frac{1}{n+k}\frac{\partial }{\partial n}\left[ \psi _{nn}+\frac{\left( 1-\psi _{n}\right) }{n+k}\right] +G_{\rm{r}}\theta +B_{\rm{r}}\sigma =\frac{k}{n+k} \left[ E_{1}\frac{\partial ^{3}\eta }{\partial s^{3}}+E_{2}\frac{\partial ^{3}\eta }{\partial t^{2}\partial s}+E_{1}\frac{\partial ^{2}\eta }{\partial t\partial s}\right] \hbox { at }n=\pm \eta , $$

(18)

$$ \theta =0,\quad\sigma =0\hbox { at }n=-\eta , $$

(19)

$$ \theta =1,\quad\sigma =1\hbox { at }n=\eta . $$

(20)

Solution of the problem

In order to solve coupled differential Eqs. (15) and (16) with the help of HPM, we construct the following equation (Abbasbandy 2006; He 2003; Wazwaz 2002):

$$ \begin{aligned} H\left( \theta ,\widetilde{p}\right)&=\left( 1-\widetilde{p}\right) \left[ \frac{\partial ^{2}\theta }{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \theta }{\partial n}-\left( \frac{\partial ^{2}\widetilde{ \theta }_{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \widetilde{\theta }_{0}}{\partial n}\right) \right] \\&\quad+\widetilde{p}\left[ \frac{\partial ^{2}\theta }{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \theta }{\partial n}\right. \left. +\left[ N_{b}\frac{\partial \sigma }{\partial n}\frac{\partial \theta }{\partial n}+N_{t}\left( \frac{\partial \theta }{\partial n}\right) ^{2} \right] =0,\right. \end{aligned} $$

(21)

$$ \begin{aligned} H\left( \sigma ,\widetilde{p}\right) &=\left( 1-\widetilde{p}\right) \left[ \frac{\partial ^{2}\sigma }{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \sigma }{\partial n}-\left( \frac{\partial ^{2}\widetilde{ \sigma }_{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \widetilde{\sigma }_{0}}{\partial n}\right) \right] \\&\quad+\widetilde{p}\left[ \frac{\partial ^{2}\sigma }{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \sigma }{\partial n}\right. \notag \left. \left. + \, \frac{N_{t}}{N_{b}}\left\{ \frac{\partial ^{2}\theta }{\partial n^{2}}+\frac{1}{n+k}\frac{\partial \theta }{\partial n}\right\}\right] =0.\right. \end{aligned} $$

(22)

Using

$$ \theta =\theta _{0}+\widetilde{p}\theta _{1}+\widetilde{p}^{2}\theta _{2}+\ldots, $$

(23)

$$ \sigma =\sigma _{0}+\widetilde{p}\sigma _{1}+\widetilde{p}^{2}\sigma _{2}+\ldots $$

(24)

With the help of Eqs. (23) and (24), equating the like powers of $\widetilde{p},$ we obtain the following systems:

Zeroth-order system

$$ \frac{\partial ^{2}\theta _{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \theta _{0}}{\partial n} =\frac{\partial ^{2}\widetilde{ \theta }_{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \widetilde{\theta }_{0}}{\partial n}, $$

(25)

$$ \frac{\partial ^{2}\sigma _{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \sigma _{0}}{\partial n} =\frac{\partial ^{2}\widetilde{ \sigma }_{0}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \widetilde{\sigma }_{0}}{\partial n}, $$

(26)

$$ \begin{aligned} \theta _{0} = 0,\hbox { \quad at }n&=&-\eta , \\ \sigma _{0} =0,\hbox { \quad at }n &=& -\eta , \\ \theta _{0} =1,\hbox { \quad at }n &=&\, \eta , \\ \sigma _{0} =1,\hbox { \quad at }n & =&\, \eta . \end{aligned} $$

First-order system

$$ \frac{\partial ^{2}\theta _{1}}{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \theta _{1}}{\partial n}+\frac{\partial ^{2}\theta _{0}}{ \partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \theta _{0}}{ \partial n}+\left[ N_{\rm{b}}\frac{\partial \sigma _{0}}{\partial n}\frac{ \partial \theta _{0}}{\partial n}+N_{\rm{t}}\left( \frac{\partial \theta _{0}}{ \partial n}\right) ^{2}\right] = 0, $$

(27)

$$ \frac{\partial ^{2}\sigma_{1}}{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \sigma _{1}}{\partial n}+\frac{\partial ^{2}\sigma _{0}}{ \partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \sigma _{0}}{ \partial n}+\frac{N_{\rm{t}}}{N_{\rm{b}}}\left[ \frac{\partial ^{2}\theta _{0}}{ \partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \theta _{0}}{ \partial n}\right] = 0, $$

(28)

$$ \begin{aligned} \theta _{1} = 0,\hbox { \quad at }n &=& -\eta ,\\ \sigma _{1} = 0,\hbox { \quad at }n &=& -\eta ,\\ \theta _{1} = 0,\hbox { \quad at }n &=&\, \eta ,\\ \sigma _{1} = 0,\hbox { \quad at }n &=& \,\eta . \end{aligned} $$

Second-order system

$$ \frac{\partial ^{2}\theta _{2}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \theta _{2}}{\partial n}+N_{\rm{b}}\left( \frac{\partial \sigma _{1}}{\partial n}\frac{\partial \theta _{0}}{\partial n}+\frac{\partial \sigma _{0}}{\partial n}\frac{\partial \theta _{1}}{\partial n}\right) +2N_{\rm{t}}\left( \frac{\partial \theta _{0}}{\partial n}\frac{\partial \theta _{1}}{\partial n}\right) =0, $$

(29)

$$ \left.\frac{\partial ^{2}\sigma _{2}}{\partial n^{2}}+\frac{1}{\left( n+k\right) }\frac{\partial \sigma _{2}}{\partial n}+\frac{N_{\rm{t}}}{N_{\rm{b}}}\left[ \frac{\partial ^{2}\theta _{1}}{\partial n^{2}}+\frac{1}{\left( n+k\right) } \frac{\partial \theta _{1}}{\partial n}\right] =0,\right. $$

(30)

$$ \begin{aligned} \theta _{2} = 0,\hbox { \quad at }n &=& -\eta , \\ \sigma _{2} = 0,\hbox { \quad at }n &=& -\eta , \\ \theta _{2} = 0,\hbox { \quad at }n &=&\, \eta , \\ \sigma _{2} = 0,\hbox { \quad at }n &=&\, \eta . \end{aligned} $$

The solutions of the above systems satisfying the boundary conditions are directly written as

$$ \theta _{0} = \widetilde{\theta }_{0}=\frac{\log \left( k-\eta \right) -\log \left( k+n\right) }{\log \left( k-\eta \right) -\log \left( k+\eta \right) }, $$

(31)

$$ \sigma _{0} =\widetilde{\sigma }_{0}=\frac{\log \left( k-\eta \right) -\log \left( k+n\right) }{\log \left( k-\eta \right) -\log \left( k+\eta \right) }, $$

(32)

$$ \begin{aligned} \theta _{1} = &\,\frac{2\left( N_{\rm{b}}+N_{\rm{t}}\right) \eta \log \left( k+n\right) }{(k^{2}-\eta ^{2})\left[ \log \left( k+n\right) -\log \left( k+n\right) \right] ^{3}}\\ &+\frac{\left(N_{\rm{b}}+N_{\rm{t}}\right) \left[ (k-\eta )(n-\eta )\log \left( k-\eta \right) -\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right] }{\left( k+n\right) \left( k^{2}-\eta ^{2}\right) \left[ \log \left( k-\eta \right) -\log \left( k+\eta \right) \right] ^{3}}, \end{aligned} $$

(33)

$$ \sigma_{1} = 0, $$

(34)

$$ \begin{aligned} \theta _{2} = & \left. -\frac{\left( N_{\rm{b}}+N_{\rm{t}}\right) \left( N_{\rm{b}}+2N_{\rm{t}}\right) }{\left( k^{2}-\eta ^{2}\right) ^{2}\left[ \log \left( k-\eta \right) -\log \left( k+\eta \right) \right] ^{5}}\left[ \eta \log \left( k+n\right) \left( 4\eta +k\log \left( k-\eta \right) -k\log \left( k+\eta \right) \right) \right. \right.\\ &-\left\{ (\left( k-\eta \right) ^{2}\left( n-\eta \right) \left( 2k+n+\eta \right) \log \left( k-\eta \right) ^{2}+\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right.\\ &\left. \left( -8\left( k+n\right) \eta +\left( 2k+n+\eta \right) \left( k+\eta \right) \log \left( k+\eta \right) \right) -2\log \left( k-\eta \right) \right.\\ &\left. \left. \left. \left( -4\left( k+n\right) \left( k-\eta \right) \left( n-\eta \right) \eta +k^{2}n\left( 2k+n\right) +( 3k^{2}+2kn+n^{2}) \eta ^{2}-\eta ^{4})\log \left( k+\eta \right) \right) \right\} \right] ,\right. \end{aligned} $$

(35)

$$ \begin{aligned} \sigma _{2} = & -\frac{2N_{\rm{t}}\left( N_{\rm{b}}+N_{\rm{t}}\right) \eta \log \left( k+n\right) }{N_{\rm{b}}\left( k^{2}-\eta ^{2}\right) \left( \log \left( k-\eta \right) -\log \left( k+\eta \right) \right) ^{3}}\\ &-\frac{N_{\rm{t}}\left( N_{\rm{b}}+N_{\rm{t}}\right) \left( \left( k-\eta \right) \left( n-\eta \right) \log \left( k-\eta \right) -\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right) }{N_{\rm{b}}\left( k+n\right) \left( k^{2}-\eta ^{2}\right) \left( \log \left( k-\eta \right) -\log \left( k+\eta \right) \right) ^{3}}. \end{aligned} $$

(36)

Invoking Eqs. (31)–(36) into Eqs. (23) and (24) and substituting $\widetilde{p}\rightarrow 1,$ we obtain the following solution:

$$ \begin{aligned} \theta \left( n,s\right) = &\frac{\log \left( k-\eta \right) -\log \left( k+n\right) }{\log \left( k-\eta \right) -\log \left( k+\eta \right) }+\frac{ 2\left( N_{\rm{b}}+N_{\rm{t}}\right) \eta \log \left( k+n\right) }{(k^{2}-\eta ^{2}) \left[ \log \left( k+n\right) -\log \left( k+n\right) \right] ^{3}}\\ &+\frac{\left(N_{\rm{b}}+N_{\rm{t}}\right) \left[ (k-\eta )(n-\eta )\log \left( k-\eta \right) -\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right] }{\left( k+n\right) \left( k^{2}-\eta ^{2}\right) \left[ \log \left( k-\eta \right) -\log \left( k+\eta \right) \right] ^{3}}\\ &\left.-\frac{\left( N_{\rm{b}}+N_{\rm{t}}\right) \left( N_{\rm{b}}+2N_{\rm{t}}\right) }{ \left( k^{2}-\eta ^{2}\right) ^{2}\left[ \log \left( k-\eta \right) -\log \left( k+\eta \right) \right] ^{5}}\left[ \eta \log \left( k+n\right) \left( 4\eta +k\log \left( k-\eta \right) -k\log \left( k+\eta \right) \right) \right. \right.\\ &-\left\{ \left( k-\eta \right) ^{2}\left( n-\eta \right) \left( 2k+n+\eta \right) \log \left( k-\eta \right) ^{2}+\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right.\\ &\left. \left( -8\left( k+n\right) \eta +\left( 2k+n+\eta \right) \left( k+\eta \right) \log \left( k+\eta \right) \right) -2\log \left( k-\eta \right) \right.\\ &\left. \left. \left. \left( -4\left( k+n\right) \left( k-\eta \right) \left( n-\eta \right) \eta +k^{2}n\left( 2k+n\right) +\left( 3k^{2}+2kn+n^{2}\right) \eta ^{2}-\eta ^{4})\log \left( k+\eta \right) \right) \right\} \right] ,\right. \end{aligned} $$

(37)

$$ \begin{aligned} \sigma \left( n,s\right) = &\frac{\log \left( k-\eta \right) -\log \left( k+n\right) }{\log \left( k-\eta \right) -\log \left( k+\eta \right) }-\frac{ 2N_{\rm{t}}\left( N_{\rm{b}}+N_{\rm{t}}\right) \eta \log \left( k+n\right) }{N_{\rm{b}}\left( k^{2}-\eta ^{2}\right) \left( \log \left( k-\eta \right) -\log \left( k+\eta \right) \right) ^{3}}\\ &-\frac{N_{\rm{t}}\left( N_{\rm{b}}+N_{\rm{t}}\right) \left( \left( k-\eta \right) \left( n-\eta \right) \log \left( k-\eta \right) -\left( k+\eta \right) \left( n+\eta \right) \log \left( k+\eta \right) \right) }{N_{\rm{b}}\left( k+n\right) \left( k^{2}-\eta ^{2}\right) \left( \log \left( k-\eta \right) -\log \left( k+\eta \right) \right) ^{3}}. \end{aligned} $$

(38)

By using mathematical software Mathematica, the exact solution for the fluid velocity is evaluated after substituting expressions for θ and σ in Eq. (14), which is discussed through graphs.

Results and discussion

The effect of various patient parameters, i.e. curvature parameter k, N_b, N_t, B_r and G_r are graphically discussed for fluid velocity, temperature profile and concentration. Figures 1, 2, 3, 4 and 5 are plotted to illustrate the effects of pertinent parameters for velocity field. In Fig. 1, the effect of curvature parameter k on fluid velocity is discussed. For small values of k, the velocity magnitude is small. The velocity increases with the increase in k. Maximum velocity is attained at the centre of the curved channel. Figure 2 displays the effect of Brownian motion parameter N_b. Small variations in N_b are taken into the account. We observe that with the increase in N_b, fluid velocity increases. The variation gets small for large values of N_b. In Fig. 3 the effects of N_t are shown, and the effect of N_t is opposite to that of N_b, i.e. fluid velocity decreases with the increase in N_t. Figure 4 shows the graphical results of velocity profile for different values of B_r. The graphs are plotted for small values of B_r; with the increase in B_r, velocity increases. Figure 5 displays the graphs for different values of G_r, and the fluid velocity increase with increase in G_r. Figures 6, 7 and 8 are graphs for temperature profile θ against n for different values of k , N_b and N_t. In Fig. 6, the effects of curvature parameter k are discussed. We note a decrease in θ with an increase in curvature parameter k, i.e. the curvature parameter affects the temperature profile up to a large extent. For very large values of k, variation in θ gets small. Figure 7 is a graph for different values of N_b, which shows increase in θ with the increase in N_b. In Fig. 8 the effect of N_t is illustrated: increase in N_t increases θ. Figures 9, 10 and 11 are the plots for concentration σ against n. Figure 9 shows the effect of curvature parameter k; we note that σ decreases with the increase in k, but it remain almost steady for k ≥ 10 onwards. Figure 10 shows the behaviour of σ for different values of N_b. It is observed that with increase in N_b, σ increases. The variation get small for large values of N_b. Figure 11 shows the effect of N_t on σ. From Fig. 11 we conclude that σ decreases with an increase in N_t. The variation grows rapidly for large values of N_t. In Fig. 12 streamlines are plotted for different values of k; here the size of the bolus decreases with the increase in k. The shape of the bolus near the upper half of the curved channel remains almost unaltered. However, near the lower half of the channel the shapes changes for different values of k. Figure  13 are the stream lines for different values of $\epsilon$ the shape of the bolus slightly changes from round to oval with the increase in values of $\epsilon.$ We note a slight change in the shape of the bolus near the upper half of the curved channel. The size and the shape of the bolus changes for different values of $\epsilon,$ near the lower half of the curved channel.

Fig. 1

The effect of curvature parameter k on velocity profile. Plots are shown for different values of k where $G_{\rm{r}}=0.2, B_{\rm{r}}=0.2, N_{\rm{t}}=0.2, N_{\rm{b}}=0.2, t=0.02, \epsilon =0.05, E_{1}=0.1, E_{2}=0.02, E_{3}=0.5, F=0.02$ and s = 0.01

Fig. 2

The behaviour for different values of N_b where $G_{\rm{r}}=0.2, B_{\rm{r}}=1, N_{\rm{t}}=1.2, k=2.5, t=0.05, \epsilon =0.05, E_{1}=0.1, E_{2}=0.02, E_{3}=0.5, F=0.02$ and s = 0.01

Fig. 3

A plot for velocity component u(n, s) against n. It shows the effect of thermophoresis parameter N_t where $G_{\rm{r}}=0.2, B_{\rm{r}}=1, N_{\rm{b}}=0.02, k=2.5, t=0.05, \epsilon =0.05, E_{1}=0.1, E_{2}=0.02, E_{3}=0.5, F=0.02$ and s = 0.01

Fig. 4

The effect of B_r where $G_{\rm{r}}=0.2, N_{\rm{b}}=0.5, N_{\rm{t}}=0.2, k=1.5, t=0.05, \epsilon =0.05, E_{1}=0.1, E_{2}=0.02, E_{3}=0.5, F=0.02$ and s = 0.01

Fig. 5

The effect of G_r where $N_{\rm{b}}=0.5, B_{\rm{r}}=0.2, N_{\rm{t}}=0.2, k=1.5, t=0.05, \epsilon =0.05, E_{1}=0.1, E_{2}=0.02, E_{3}=0.5, F=0.02$ and s = 0.01

Fig. 6

A plot for temperature $\theta \left( n,s\right)$ against n. It shows the effects for different values of k where $N_{\rm{t}}=0.5, N_{\rm{b}}=0.5, t=0.05, \epsilon =0.05$ and s = 0.3

Fig. 7

The effect of N_b where $N_{\rm{t}}=0.5, k=2, t=0.05, \epsilon =0.05$ and s = 0.3

Fig. 8

The effect of N_t where $N_{\rm{b}}=0.5,k=2,t=0.05,\epsilon =0.05$ and s = 0.3

Fig. 9

Plot for $\sigma \left( n,s\right)$ against n. It shows the effect of k where $N_{\rm{t}}=0.05, N_{\rm{b}}=0.05, t=0.05, \epsilon =0.05$ and s = 0.01

Fig. 10

The effect of N_b where $N_{\rm{t}}=2, k=5, t=0.05, \epsilon =0.05$ and s = 0.01

Fig. 11

The effect of N_t where $N_{\rm{b}}=0.01, k=5, t=0.05, \epsilon =0.05$ and s = 0.01

Fig. 12

The streamlines are plotted for against different values of curvature parameter k, i.e. a k = 2, b k = 4, c k = 6, d k = 8 while $B_{\rm{r}}=0.5, G_{\rm{r}}=0.5, N_{\rm{t}}=0.5, N_{\rm{b}}=2.5, t=0, \epsilon =0.05, E_{1}=1, E_{2}=0.5, E_{3}=0.1$ and F = 0.02

Fig. 13

The streamlines are plotted for against different values of $\epsilon, {\rm{i.e.}}\; {\mathbf{a}}\; \epsilon \, =\, 0.01, {\mathbf{b}}\; \epsilon =\, 0.02, {\mathbf{c}}\; \epsilon =\, 0.05, {\mathbf{d}}\; \epsilon =\, 0.1$ while B_r = 0.5, G_r = 0.5, N_t = 0.5, N_b = 2.5, t = 0, k = 2, E₁ = 1, E₂ = 0.5, E₃ = 0.1 and F = 0.2