Peristaltic flow of a micropolar fluid with nano particles in small intestine

Abstract

The present article analyzed the peristaltic flow of a nanofluid in a uniform tube for micropolar fluid. The governing equations for proposed model are developed in cylindrical coordinates system. The flow is discussed in a wave frame of reference moving with velocity of the wave c. Under the assumptions of longwave length the reduced coupled nonlinear differential equations of momentum, energy, and concentrations are solved by Homotopy perturbation method is used to get the solutions for velocity, temperature, nano particle, microrotation component. The solutions consists Brownian motion number N_b, thermophoresis number N_t, local temperature Grashof number B _r and local nano particle Grashof number G _r . The effects of various parameters involved in the problem are investigated for pressure rise, pressure gradient, temperature and concentration profile. Five different waves are taken into account for analysis. Streamlines have been plotted at the end of the article.

Introduction

Micropolar fluids are fluids with microstructure belonging to a class of fluids with nonsymmetrical stress tensor referred to as polar fluids. Physically, they represent fluids consisting of randomly oriented particles suspended in a viscous medium, and they are important to engineers and scientists working with hydrodynamic-fluid problems and phenomena (Grzegorz et al. 1998) Eringen (1996) was first who introduced the concept of simple micropolar fluids to characterize concentrated suspensions of neutrally buoyant deformable particles in a viscous fluid, where the individuality of substructures affects the physical outcome of the flow. He coat that micropolar fluid describe the microrotation effects to the microstructure model After the first investigation of Eringen (1996) this model has attracted the attention of many scientist, mathematician, physicists and engineers, because the well known Navier–Stokes’ theory does not describe previously the physical properties of polymer fluids, colloidal solutions, suspension solutions, liquid crystals, animals blood, exotic lubricants and fluid containing small additives. A micropolar model for axisymmetric blood flow through an axially nonsymmetreic but radially symmetric mild stenosis tapered artery is presented by Mekheimer and El Kot (2008). They discussed that a subclass of these microfluids is known as micropolar fluids where the fluid microelements are considered to be rigid. Basically, these fluids can support couple stresses and body couples and exhibit microrotational and microinertial effects. Nadeem et al. (2010) analyzed the effects of heat transfer on a peristaltic flow of a micropolar fluid in a vertical annulus.

Recently, peristaltic problems has gained a considerable attention of researchers because of its applications in physiology, engineering and industry i.e. urine transport from kidney to bladder, swallowing food through the esophagus, chyme motion in the gastrointestinal tract, vasomotion of small blood vessels and movement of spermatozoa in human reproductive tract. There are many engineering processes as well in which peristaltic pumps are used to handle a wide range of fluids particularly in chemical and pharmaceutical industries. This mechanism is also used in the nuclear industry. The recent developments on the topic include (Mekheimer and Abd Elmaboud 2008; Vajravelu et al. 2007; Mekheimer 2008; Srinivas and Kothandapani 2008; Kothandapani and Srinivas 2008; Srinivas et al. 2009; Nadeem 2009).

Nano fluid is a fluid containing nanometer-sized particles, called nano particles. These fluids are engineered colloidal suspensions of nano particles in a base fluid (Buongiorno 2006). The nano particles used in nano fluids are typically made of metals, oxides, carbides, or carbon nano tubes. Nano fluids have novel properties that make them potentially useful in many applications in heat transfer, including microelectronics, fuel cells, pharmaceutical processes, and hybrid-powered engines (Das et al. 2007). In engineering devices it has been widely used for engine cooling/vehicle thermal management, domestic refrigerator, chiller, heat exchanger, and nuclear reactor, in grinding, in machining, in Space, defense and ships, and in Boiler flue gas temperature reduction. They exhibit enhanced thermal conductivity and the convective heat transfer coefficient compared to the base fluid (Sadik and Pramuanjaroenkij 2009) In peristaltic literature only one investigation has been done by Akbar (2011) They studied the peristaltic flow of a nano fluid in an endoscope. They observed that with the increase in the Brownian motion parameter N_b and the thermophoresis parameter N_t temperature profile increases.

Motivated by the possible applications and previous studies regarding the micropolar fluid and nano fluid, we have presented the peristaltic flow of a micropolar fluid in a uniform tube with nano particles. Equations of momentum, energy, and concentrations are coupled so Homotopy perturbation method is used to get the solutions for velocity, temperature, nano particle, microrotation component. The solutions consists Brownian motion number N_b, thermophoresis number N_t, local temperature Grashof number B _r and local nanoparticle Grashof number G _r . The effects of various parameters involved in the problem are investigated for pressure rise, pressure gradient, temperature and concentration profile. Five different waves are taken into account for analysis. Streamlines have been plotted at the end of the article.

Physical model and fundamental equations

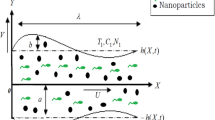
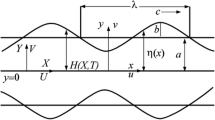
Let us consider the flow of an incompressible micropolar fluid in a uniform tube with nano particles. The flow is generated by sinusoidal wave trains propagating with constant speed c₁ along the walls of the tube. Heat transfer along with nanoparticle phenomena has been taken into account. The walls of the tube are maintaining temperature $\bar{T}_{0}$ and nanoparticle volume fraction $\bar{C}_{0}$, while at the centre we have used symmetry condition on both temperature and concentration. The geometry of the wall surface is defined as

$$ \bar{h} = {\mathbf{a}} + b\sin \frac{2\pi }{\lambda }\left( {\bar{X} - c_{1} \bar{t}} \right), $$

(1)

where a is the radius of the tube, b is the wave amplitude, λ is the wavelength, c₁ is the propagation velocity and $\bar{t}$ is the time. We are considering the cylindrical coordinate system $(\bar{R},\bar{X})$, in which $\bar{X}$-axis lies along the center line of the tube and $\bar{R}$ is transverse to it.

Introducing a wave frame ($\bar{r},\bar{x}$) moving with velocity c₁ away from the fixed frame $(\bar{R},\bar{X})$ by the transformations

$$ \bar{x} = \bar{X} - c_{1} \bar{t},\quad \bar{r} = \bar{R}, $$

(2)

$$ \bar{v}_{\text{r}} = \bar{V}_{\text{r}} - c_{1} ,\quad \bar{v}_{x} \, = \bar{V}_{x} , $$

(3)

in which $\bar{U},\bar{W}$ and $\bar{u},\bar{w}$ are the velocity components in the radial and axial directions in the fixed and moving coordinates respectively.

Dimensionless variables are defined as

$$ \begin{aligned} R = & \frac{{\bar{R}}}{a},\quad r = \frac{{\bar{r}}}{a},\quad Z = \frac{{\bar{Z}}}{\lambda },\quad z = \frac{{\bar{z}}}{\lambda },\quad W = \frac{{\bar{W}}}{{c_{1} }},\quad w = \frac{{\bar{w}}}{{c_{1} }},\quad U = \frac{{\lambda \bar{U}}}{{ac_{1} }},\quad u = \frac{{\lambda \bar{u}}}{{ac_{1} }}, \quad P = & \frac{{a^{2} \bar{P}}}{{c_{1} \lambda \mu }},\quad \theta = \frac{{\left( {\bar{T} - \bar{T}_{0} } \right)}}{{\bar{T}_{0} }},\quad t = \frac{{c_{1} \bar{t}}}{\lambda },\quad \delta = \frac{a}{\lambda },\quad Re = \frac{{2\rho c_{1} a}}{\mu },\quad \sigma = \frac{{\left( {\bar{C} - \bar{C}_{0} } \right)}}{{\bar{C}_{0} }}, \quad h = & \frac{{\bar{h}}}{a} = 1 + \frac{\lambda kz}{{a_{0} }} + \phi \sin 2\pi z,\quad \alpha = \frac{k}{{\left( {\rho c} \right)_{f} }},\quad N_{\text{b}} = \frac{{\left( {\rho c} \right)_{\text{p}} D_{B} \bar{C}_{0} }}{{\left( {\rho c} \right)_{\text{f}} }},\quad v_{\text{r}} = \frac{{\lambda \bar{v}_{\text{r}} }}{ac},\quad j = \frac{{\bar{j}}}{{a^{2} }}. \\ N_{\text{t}} = & \frac{{\left( {\rho c} \right)_{\text{p}} D_{{\bar{T}}} \bar{C}_{0} }}{{\left( {\rho c} \right)_{\text{f}} \alpha }},\quad P_{r} = \frac{\nu }{\alpha },\quad G_{r} = \frac{{g\alpha a^{3} \bar{T}_{0} }}{{\nu^{2} }},\quad B_{{r}} = \frac{{g\alpha a^{3} \bar{C}_{0} }}{{\nu^{2} }}.v_{x} = \frac{{\bar{v}_{x} }}{c},\quad v_{\theta } = \frac{a}{c}\bar{v}_{\theta } . \\ \end{aligned} $$

(4)

The equations of an incompressible micropolar fluid (Nadeem et al. 2010) with nano particle (Akbar 2011) in dimensionless form under long wave length assumptions are defined

$$ \frac{{\partial v_{\text{r}} }}{\partial r} + \frac{{v_{\text{r}} }}{r} + \frac{{\partial v_{x} }}{\partial x} = 0 $$

(5)

$$ 0 = \frac{\partial P}{\partial x}, $$

(6)

$$ o = - \frac{\partial P}{\partial x} + \frac{1}{{\left( {1 - N} \right)}}\left( {\frac{N}{r}\frac{{\partial \left( {rv_{\theta } } \right)}}{\partial r} + \frac{{\partial^{2} v_{x} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial v_{x} }}{\partial r} + \delta^{2} \frac{{\partial^{2} v_{x} }}{{\partial x^{2} }}} \right) + G_{r} \Uptheta + B_{r} \sigma , $$

(7)

$$ 0 = - 2v_{\theta } + \left( { - \frac{{\partial v_{x} }}{\partial r}} \right) + \frac{2 - N}{{m^{2} }}\left( {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \left( {rv_{\theta } } \right)}}{\partial r}} \right)} \right), $$

(8)

$$ 0 = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \Uptheta }{\partial r}} \right) + N_{\text{b}} \frac{\partial \sigma }{\partial r}\frac{\partial \Uptheta }{\partial r} + N_{\text{t}} \left( {\frac{\partial \Uptheta }{\partial r}} \right)^{2} , $$

(9)

$$ 0 = \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \sigma }{\partial r}} \right)} \right) + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \Uptheta }{\partial r}} \right)} \right). $$

(10)

in which N is the coupling number m is the micropolar parameter, P _r , N_b, N_t, G _r and B _r are the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.

The corresponding boundary conditions in dimensionless form are

$$ v_{\theta } = 0,\quad \frac{{\partial v_{x} }}{\partial r} = 0,\quad \frac{\partial \theta }{\partial r} = 0,\quad \frac{\partial \sigma }{\partial r} = 0,\quad {\text{at}}\quad r = 0, $$

(11a)

$$ v_{\theta } = 0,\quad v_{x} = - 1,\quad \theta = 0,\quad \sigma = 0,\quad {\text{at}}\quad r = h = 1 + \phi \sin 2\pi x. $$

(11b)

Solution of the problem

Homotopy perturbation solution

The combination of the perturbation method and the homotopy method is called the HPM (an analytical technique) (Akbar 2011; He 1998, 1999, 2005), which eliminates the drawbacks of the traditional perturbation methods while keeping all their advantages.

For homotopy perturbation method we have taken $L = \tfrac{1}{r}\tfrac{\partial }{\partial r}\left( {r\tfrac{\partial }{\partial r}} \right)$ as the linear operator. We can define the initial guesses as given below which satisfies the boundary conditions

$$ \begin{aligned} \theta_{10} \left( {r,x} \right) & = \left( {\frac{{r^{2} - h^{2} }}{4}} \right),\quad \sigma_{10} \left( {r,x} \right) = - \left( {\frac{{r^{2} - h^{2} }}{4}} \right)\frac{{N_{\text{t}} }}{{N_{\text{b}} }}, \\ v_{\theta 10} \left( {r,x} \right) & = \left( {\frac{{r^{5} - h^{5} }}{50}} \right)\frac{{{\text{d}}P_{0} }}{{{\text{d}}x}}\frac{{m^{2} (1 - N)}}{2 - N}, \\ \end{aligned} $$

(12)

Let us define

$$ \Uptheta \left( {r,q} \right) = \Uptheta_{0} + q\Uptheta_{1} + q_{2}^{2} \Uptheta_{2} + \cdots $$

(13)

$$ \sigma \left( {r,q} \right) = \sigma_{0} + q\sigma_{1} + q^{2} \sigma_{2} + \cdots $$

(14)

$$ v_{\theta } \left( {r,q} \right) = v_{\theta 0} + qv_{\theta 1} + q_{2}^{2} v_{\theta 2} + \cdots $$

(15)

Adopting the same procedure as done by (Akbar 2011; He 1998, 1999, 2005), the solution for temperature, nanoparticle phenomena and microrotation component can be written as for q = 1.

$$ \begin{aligned} \theta \left( {r,x} \right) = & \left( {\frac{{r^{2} - h^{2} }}{4}} \right) + N_{t} \left( {\frac{{r^{3} - h^{3} }}{18}} \right) - N_{t} \left( {\frac{{r^{4} - h^{4} }}{64}} \right) + \frac{1}{4}\left( {h^{2} - r^{2} } \right) \\ & \quad - N_{\text{b}} \left( {\frac{{r^{4} - h^{4} }}{64}} \right) + N_{\text{t}} N_{\text{b}} \left( {\frac{{r^{5} - h^{5} }}{300}} \right) - N_{\text{t}} N_{\text{b}} \left( {\frac{{r^{6} - h^{6} }}{1152}} \right), \\ \end{aligned} $$

(16)

$$ \begin{aligned} \sigma \left( {r,x} \right) = & - \left( {\frac{{r^{2} - h^{2} }}{4}} \right)\frac{{N_{\text{t}} }}{{N_{\text{b}} }} + \frac{1}{4}\left( {h^{2} - r^{2} } \right) - \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\left( {\frac{{h^{2} - r^{2} }}{4}} \right) \\ & \quad - \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\left( {\frac{{N_{\text{t}} \left( {r^{3} - h^{3} } \right)}}{18} - \frac{{N_{\text{t}} \left( {r^{4} - h^{4} } \right)}}{64} + \frac{1}{4}\left( {h^{2} - r^{2} } \right)} \right), \\ \end{aligned} $$

(17)

$$ \begin{aligned} v_{\theta } \left( {r,x} \right) = & \left( {\frac{{r^{5} - h^{5} }}{50}} \right)\frac{{{\text{d}}P}}{{{\text{d}}x}}\frac{{m^{2} (1 - N)}}{2 - N} - \frac{{h^{5} m^{2} (N - 1)\left( {r^{2} - h^{2} } \right)}}{200(N - 2)}\frac{{{\text{d}}P_{0} }}{{{\text{d}}x}} + \frac{{a_{6} \left( {r^{5} - h^{5} } \right)}}{25} \\ & \quad + \frac{{a_{4} \left( {r^{8} - h^{8} } \right)}}{25} + \frac{{50a_{5} \left( {N - 2} \right)\left( {r^{7} - h^{7} } \right)}}{2450(N - 2)} + \frac{{m^{2} (N - 1)\left( {r^{7} - h^{7} } \right)}}{2450(N - 2)}\frac{{{\text{d}}P_{0} }}{{{\text{d}}x}} \\ & \quad + \frac{{a_{3} \left( {r^{9} - h^{9} } \right)}}{81} + \frac{{a_{2} \left( {r^{10} - h^{10} } \right)}}{100} + \frac{{a_{1} \left( {r^{11} - h^{11} } \right)}}{121}, \\ \end{aligned} $$

(18)

Substituting Eqs. (16)–(18) in Eq. (7), the solution for velocity and pressure gradient can be written as follows

$$ \begin{aligned} v_{x} \left( {r,x} \right) = & - 1 + a_{8} \left( {r - h} \right) + \frac{{m^{2} h^{5} (N - 1)N(r - h)}}{50(N - 2)}\frac{{{\text{d}}P}}{{{\text{d}}x}} + \frac{1}{4}\left( {2a_{9} + \left( {1 - N} \right)\frac{{{\text{d}}P}}{{{\text{d}}x}}} \right) \\ & \quad \left( {r^{2} - h^{2} } \right) + \frac{{a_{10} \left( {r^{3} - h^{3} } \right)}}{3} + \frac{{a_{11} \left( {r^{4} - h^{4} } \right)}}{4} + \frac{{a_{12} \left( {r^{5} - h^{5} } \right)}}{5} + \frac{{a_{13} \left( {r^{6} - h^{6} } \right)}}{6} \\ & \quad - \frac{{m^{2} (N - 1)N\left( {r^{6} - h^{6} } \right)}}{300(N - 2)}\frac{{{\text{d}}P}}{{{\text{d}}x}} + \frac{{a_{14} \left( {r^{7} - h^{7} } \right)}}{7} + \frac{{a_{15} \left( {r^{8} - h^{8} } \right)}}{8} - \frac{{a_{16} \left( {r^{9} - h^{9} } \right)}}{9} \\ & \quad + \frac{{a_{17} \left( {r^{10} - h^{10} } \right)}}{10} + \frac{{a_{18} \left( {r^{11} - h^{11} } \right)}}{11} + \frac{{a_{19} \left( {r^{12} - h^{12} } \right)}}{12}, \\ \end{aligned} $$

(19)

$$ \frac{{{\text{d}}P}}{{{\text{d}}x}} = \frac{{F_{1} + h - a_{20} }}{{a_{21} }}. $$

(20)

where a₁ to a₂₁ are constants evaluated using Mathematica.

Flow rate in dimensionless form can be written as explained by (Akbar 2011)

$$ F_{1} = 2Q - \frac{{\phi^{2} }}{2} - 1, $$

The pressure rise ΔP and friction force F are defined as follows

$$ \Updelta P = \mathop \smallint \limits_{0}^{1} \frac{{{\text{d}}P}}{{{\text{d}}x}}{\text{d}}x,\, $$

(21)

$$ F = \mathop \smallint \limits_{0}^{1} h^{2} \left( { - \frac{{{\text{d}}P}}{{{\text{d}}x}}} \right){\text{d}}x, $$

(22)

where $\tfrac{{\rm d}P}{{\rm d}x}$ is defined in Eq. (20).

For analysis, we have considered five waveforms namely sinusoidal, multi-sinusoidal, triangular, square and trapezoidal. The non-dimensional expressions for these wave forms are given by

• 1. Sinusoidal wave:

  $$ h\left( z \right) = 1 + \phi \sin \left( {2\pi z} \right) $$

• 2. Multi sinusoidal wave:

  $$ h\left( z \right) = 1 + \phi \sin \left( {2m_{1} \pi z} \right) $$

• 3. Triangular wave:

  $$ h\left( z \right) = 1 + \phi \left\{ {\frac{8}{{\pi^{3} }}\mathop \sum \limits_{m = 1}^{\infty } \frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {2m - 1} \right)^{2} }}\sin \left( {2\pi \left( {2m - 1} \right)z} \right)} \right\} $$

• 4. Square wave:

  $$ h\left( z \right) = 1 + \phi \left\{ {\frac{4}{\pi }\mathop \sum \limits_{m = 1}^{\infty } \frac{{\left( { - 1} \right)^{n + 1} }}{2m - 1}\cos \left( {2\pi \left( {2m - 1} \right)z} \right)} \right\} $$

• 5. Trapezoidal wave:

  $$ h\left( z \right) = 1 + \phi \left\{ {\frac{32}{{\pi^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \frac{{\sin \tfrac{\pi }{8}\left( {2m - 1} \right)}}{{\left( {2m - 1} \right)^{2} }}\sin \left( {2\pi \left( {2m - 1} \right)z} \right)} \right\} $$

Numerical results and discussion

In this section we have presented the solution for the peristaltic flow of a micropolar fluid with nano particles passing a uniform tube graphically. The expression for pressure rise ΔP is calculated numerically using mathematics software. The effects of various parameters on the pressure rise ΔP are shown in Figs. 1a, 2, 3, 4a for various values of amplitude ratio ϕ, coupling number N, micropolar parameter m and thermophoresis parameter N_t. It is observed from Figs. 1a, 2, 3, 4a that pressure rise increases with the increase in amplitude ratio ϕ, coupling number N and micropolar parameter m while the pressure rise decreases with the increase in thermophoresis parameter N_t. Peristaltic pumping region is (−1 ≤ Q ≤ 0.3) for Fig. 1 and for Figs. 2, 3, 4 peristaltic pumping region is (−1 ≤ Q ≤ 0) and augmented pumping region is (0.31 ≤ Q ≤ 1) and (0.1 ≤ Q ≤ 1), respectively. Figures 1b, 2, 3, 4b represent the behavior of frictional forces. It is depicted that frictional forces have an opposite behavior as compared to the pressure rise. Effects of temperature profile have been shown through Fig. 5a, b. It is seen that with the increase in the Brownian motion parameter N_b and the thermophoresis parameter N_t, temperature profile increases and maximum temperature occurs at r = 0. The nanoparticle phenomena σ for different values of the Brownian motion parameter N_b and the thermophoresis parameter N_t are shown in Fig. 6a and b. We have observed that the nanoparticle phenomena increase with an increase in Brownian motion parameter N_b and decrease with an increase in the thermophoresis parameter N_t. Figure 7a–e are prepared to see the behavior of pressure gradient for different wave shapes. It is observed from the figures that for zε[0, 0.5] and [1.1, 1.5] the pressure gradient is small, and large pressure gradient occurs for zε[0.5, 1], moreover, it is seen that with increase in ϕ pressure gradient increases. Figure 7 shows the streamlines for different wave forms. It is observed that the size of the trapped bolus in triangular wave is small as compared to the other waves. It is also depicts that streamlines and pressure gradient takes the form of the wave which is taken into account (Fig. 8).

Fig. 1

a Pressure rise, b frictional force for N = 0.8, m = 0.8, G _r  = 0.5, B _r  = 0.5, N_t = 0.5, N_b = 10

Fig. 2

a Pressure rise. b Frictional force for ϕ = 0.2, m = 0.8, G _r  = 0.5, B _r  = 0.5, N_t = 0.5, N_b = 10

Fig. 3

a Pressure rise, b frictional force for ϕ = 0.2, N = 0.8, G _r  = 0.5, B _r  = 0.5, N_t = 0.5, N_b = 0.4

Fig. 4

a Pressure rise, b frictional force for ϕ = 0.2, N = 0.8, G _r  = 0.5, B _r  = 0.5, m = 0.5, N_b = 0.4

Fig. 5

Temperature profile for aN_t = 0.2, bN_b = 0.2, other parameters are K = 0.04, λ = 0.05, a₀ = 0.03, ϕ = 0.1, z = 0.2

Fig. 6

Concentration profile for aN_t = 0.07, bN_b = 0.16, other parameters are K = 0.04, λ = 0.05, a₀ = 0.03, ϕ = 0.1, z = 0.2

Fig. 7

Pressure gradient versus z for a sinusoidal wave, b multisinusoidal wave, c square wave, d triangular wave, e trapezoidal wave for N = 0.8, m = 0.8, G _r  = 0.5, B _r  = 0.5, N_t = 0.5, N_b = 10, Q = −0.2

Fig. 8

Streamlines for a sinusoidal wave, b multisinusoidal wave, c square wave, d triangular wave, e trapezoidal wave for N = 0.8, m = 0.8, G _r  = 0.5, B _r  = 0.5, N_t = 0.5, N_b = 10, Q = −0.2

Conclusion

This study examines the peristaltic flow and the effects of heat transfer on a peristaltic flow of a micropolar fluid in a vertical annulus. Long wavelength assumption is used. The main points of the performed analysis are as follows:

• 1. It is observed that pressure rise increases with the increase in amplitude ratio ϕ, coupling number N and micropolar parameter m while the pressure rise decreases with the increase in thermophoresis parameter N_t.

• 2. The frictional forces have an opposite behaviour as compared to the pressure rise.

• 3. It is seen that with the increase in the Brownian motion parameter N_b and the thermophoresis parameter N_t temperature profile increases.

• 4. Effects of Brownian motion parameter N_b and the thermophoresis parameter N_t on concentration profile are opposite.

• 5. Pressure gradient increases with an increase inψ.

• 6. It is depicts that pressure gradient takes the form of the wave which is taken into account.

• 7. The size of trapped bolus for triangular wave is small as compared to the other waves.