Introduction

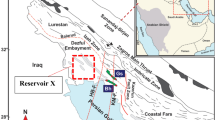
October Field is located in the north-central part of the Gulf of Suez, Egypt (Fig. 1) (EGPC 1996), with latitude from 28° 48′ 00" N to 28° 53′ 00'' N and longitude from 33° 03′ 00'' E to 33° 08′ 00'' E. October Field was discovered in 1977, the GS 195–1 well (later renamed October A-1) was drilled to test a large, NW-trending, fault-bounded structure that had been identified from a 1976 regional seismic survey in the October area. The well October A-1 was targeting Nukhul as primary target and Nubia as secondary target. The October Field, positioned approximately 25 km to the north of the vast Belayim field, exhibits a structural configuration characterized by elongated faulted blocks. These faulted blocks align in a northwest–southeast trend and have a northeast dip. These pre-Miocene faulted blocks extend along the strike of the field for approximately 20 km (Zahran 1986; EGPC 1996; Kassem et al. 2021; Khattab et al. 2023).

Fig. 1
figure 1

Location map of the study area, Gulf of Suez, Egypt (EGPC 1996)

Full size image

Nubia formation is considered as a major reservoir in Gulf of Suez especially in October Field. It contains around 1163 MMBO reserves yet it still possesses an attractive hydrocarbon potential (EGPC 1996).

Machine-learning is one of the state-of-art techniques in oil and gas industry. It represents one of the most powerful techniques in terms of cost, time and accuracy. Many authors applied machine-learning techniques in different areas in the world and achieved adequate results (Altunbay et al. 2018; Wang et al. 2020; Rajabi et al. 2021, 2023; Gao et al. 2023; Ali et al. 2022, 2023; Mustafa et al. 2022; Thanh et al. 2022, 2023; Amjad et al. 2023; Manzoor et al. 2023) and for reservoir evaluation (Ehsan et al. 2019, 2023).

Rock typing is used as a tool for predicting the spatial distribution of petrophysical and reservoir engineering parameters on a field-wide basis from studies of control wells (Altunbay et al. 2018; Radwan et al. 2021a, 2022; Nabawy et al. 2021; El-Gendy et al. 2022; Marghani et al. 2023; Ismail et al. 2023). Therefore, it is an essential part of the static and dynamic models of an asset. There are varieties of approaches, from multidisciplinary origins to rock typing. Rock typing plays a crucial role in both geological and engineering studies pertaining to oil and gas fields. It serves as a fundamental aspect of reservoir characterization and the overall development of the field. However, extending the classification from cored intervals to all wells using traditional methods based on geologic origin analysis poses significant challenges in establishing a quantitative relationship. Rezaee and Ekundayo (2022) and Wang et al. (2020) have attempted to predict rock types using machine-learning algorithms, yet neither of them has developed a simple model that only uses four input well logging curves. Also, either of them did not choose the same machine-learning algorithm chosen in this paper, and of course, the hyper-parameters of this algorithm are different than those of the one discussed here in this paper. Finally, either of both researches were conducted in October Field, Gulf of Suez area.

The current study aiming to apply the workflow of using machine-learning algorithms to predict rock types in un-cored wells and intervals in a very simple manner in terms of features/inputs required. Also, showing the results of such workflow and comparing them to other related permeability finding tools such as routine core analysis and nuclear magnetic resonance logging tool (NMR) to find the optimum permeability prediction. This will help to have some sort of realization of the permeability of the targeted reservoir, thus enhancing the choice of perforation intervals, a crucial decision in the oil and gas industry that has a massive effect on hydrocarbon production.

Literature review

On the contrary to physical and empirical methods for permeability prediction whether Kozney–Carman models, nuclear magnetic resonance or induced polarization used in Weller et al. (2014), which use physical and geological approaches as pore radius, tortuosity, polarization and relaxation times along with other physical and geological approaches. Machine-learning models are mathematical and statistical models which are numerical in nature, even when dealing with the physical input features, it only uses their values to establish an array of numbers from which it can learn and, therefore, predict.

In addition, the machine-learning model used in Wang et al. (2020) is a mere decision tree, which is a building unit to the random forest, which, in turn, is a building unit to the extreme gradient boosting algorithm which is used in this study. This reflects the superiority of the algorithm used in the present study compared to the decision tree. Also, the input features required for the former study are different, and its number exceeds that of the present study as the number of input features required for the former study is five inputs features which are porosity, shale volume, water saturation, density log and shallow resistivity log compared to the four input features required for the present study which are gamma-ray log, density log, neutron log and sonic log.

Rezaee and Ekundayo (2022) use four algorithms: multi-layer perceptron/neural network, support vector regressor, random forest and gradient boosting regressor, the last algorithm is a similar algorithm to the algorithm used in the present study. Input features used for this similar algorithm were seven which are shale volume, density log, photoelectric effect log, neutron log, sonic log, deep resistivity log and effective porosity log, yet the accuracy was less than that of the present study as the accuracy R2 correlation score dropped from above 0.9 to below 0.7, while in the present study, the R2 correlation score dropped from 1 to 0.728 in the training and validation phases, respectively.

Therefore, this is a new method in predicting permeability where it uses statistical and mathematical approaches through machine-learning algorithms with the addition of simplicity of the hyper-parameters, and the number of input features required in addition to the commonality of these input features and enhanced accuracy.

Geological setting

The Gulf of Suez region is a narrow water body situated in a north/northwest–south/southeast direction, serving as a natural division between the northeastern part of the African continent and the Sinai Peninsula. This region is part of the northern compartment of the Red Sea rift. The Gulf of Suez area holds significant importance in Egypt’s exploration efforts and stands as the most extensively drilled and explored portion. It encompasses over 80 oil fields, hosting reservoirs ranging in age from the Precambrian period to the Quaternary period (Elsayed et al. 2021; El Nady et al. 2015). The Gulf of Suez basin is categorized into three distinct structural provinces, determined by the regional dip direction of its tilted fault blocks (Bosworth and McClay 2001). The northern and southern provinces exhibit a southwestward dip, while the central province demonstrates a northeastward dip. Separation between both provinces occurs via two accommodation zones that trend in a northeast direction (Moustafa 1976; Patton et al. 1994). With a length of approximately 320 km and a width ranging from 60 to 25 km, the Gulf of Suez basin is classified as a rift basin. It is characterized by intricate tectonic activity, wherein faulted blocks are delineated by significant northwest–southeast faults (Clysmic direction), along with secondary southwest–northeast trending faults. This region is renowned as the most prolific oil rift basin in both the Middle East and Africa, boasting high levels of oil production (Elsayed et al. 2021; El Nady et al. 2015).

October Field is located in the north-central part of the Gulf of Suez, Egypt (Fig. 1) (EGPC 1996), with latitude from 28° 48′ 00" N to 28° 53′ 00'' N and longitude from 33° 03′ 00'' E to 33° 08′ 00'' E. October Field was discovered in 1977, the GS 195–1 well (later renamed October A-1) was drilled to test a large, NW-trending, fault-bounded structure that had been identified from a 1976 regional seismic survey in the October area. The October Field, positioned approximately 25 km to the north of the vast Belayim field, exhibits a structural configuration characterized by elongated faulted blocks. These faulted blocks align in a northwest–southeast trend and have a northeast dip. These pre-Miocene faulted blocks extend along the strike of the field for approximately 20 km (Zahran 1986; EGPC 1996; Kassem et al. 2021; Khattab et al. 2023). The field is bounded to the west by a sequence of normal faults with downthrown displacement to the west, it is also divided into a main southern block and a secondary northern block (El‐Ghamri et al. 2002; Radwan et al. 2021b).

The Miocene Nukhul formation, which was produced from the onshore Abu Rudeis Field, 10–15 km to the east, was the main objective, with the Paleozoic–Cretaceous Nubia sandstones as a secondary target (Lelek et al. 1992; Radwan et al. 2020). The Nukhul reservoir was absent, but the Nubia contained 541 ft of net oil pay, which tested 29.6°API oil at 4562 Barrel Oil Per Day (BOPD) on a 34/64 in. choke. Logs showed a single oil water contact (OWC) at 11,670 ft True Vertical Depth Sub Sea (TVDSS) (Zahran 1986). The wells were put on production in October 1977 (Zahran 1986), and a production platform was installed in 1979 (Borling et al. 1996). The primary oil production at the October Field is derived from the sandstones within the Paleozoic–Cretaceous Nubia Formation (Lelek et al. 1992). In 1989, additional reserves were discovered in a smaller, separate Nubia pool with a shallower OWC in the North October Area by the discovery well, GS172-1 (October J-1), which penetrated Nubia sandstones at 10,723 ft TVDSS and tested at a rate of 7880 BOPD from 254 ft of net oil pay. In the October Field, the basal pre-rift reservoir section is primarily composed of various sandstones known as the “Nubian Sandstone.” The Nubia Formation ranges in age from the Paleozoic to the Lower Cretaceous and unconformably overlies the Precambrian crystalline basement and is conformably overlain by Upper Cretaceous shales of the Nezzazat Group (Hussein et al. 2017; Zahran 1986). Figure 2 shows the litho-stratigraphic column of the October Field (Peijs et al. 2012).

Fig. 2
figure 2

Tectonostratigraphic history and stratigraphic megasequences of Gulf of Suez (Peijs et al. 2012)

Full size image

Deaf (2009) suggested that during the late Cretaceous period in the Gulf of Suez, there was a notable marine transgression, the lower part of the Gulf of Suez sequence, which is of the latest early Cretaceous age, appears to have been deposited in a continental basin. The late Cretaceous sedimentary record in the Gulf of Suez demonstrates a transition from continental alluvial deposits to marine carbonate sequences.

The Nubian Sandstone can be further subdivided into different groups based on lithological characteristics. The Lower Paleozoic Qebliat Group, which corresponds to the previously used terms Nubia “D” and “C,” is dominated by sandstone lithologies. The Carboniferous Ataqa Group, equivalent to the Nubia “B” and the lower portion of the Nubia “A,” consists of both dolomites and sandstones. This group exhibits a mixture of carbonate and siliciclastic facies. The Lower Cretaceous Malha Formation represents the upper part of the Nubia “A” and is primarily composed of coarse-grained sandstones. These sandstones within the Malha Formation exhibit a coarser grain size compared to the other units.

Overall, the Nubian Sandstone in the October Field comprises different lithological units, including the sandstone-dominated Lower Paleozoic Qebliat Group, the dolomites and sandstones of the Carboniferous Ataqa Group and the coarse-grained sandstones of the Lower Cretaceous Malha Formation. These sandstone units form the dominant reservoir section underlying the October Field (Hasouba et al. 1992; El‐Ghamri et al. 2002).

Methods and techniques

The dataset available for the current study includes the complete set of logging data for four wells (OCT-A2B, OCT-B8, OCT-B6 and OCT-K5). The logging data include gamma-ray (GR), caliper (CALI) deep and medium resistivity (RD and RM), neutron (NPHI), density (RHOB) and sonic (DT). The logging data were used for formation evaluation and as inputs for AI technique. As for the core data, routine core analysis (RCAL) is available for all three cored wells (OCT-A2B, OCT-B8 and OCT-B6), while special core analysis (SCAL) is available for only two wells (OCT-A2B and OCT-B6). The core data were used for the rock typing of the formation so that the rock types are used as input for AI technique. For the un-cored well OCT-K5, same set of logs is available except for the sonic log is missing in its dataset but it has nuclear magnetic resonance log (NMR) available. NMR log is used to calculate permeability to compare it with permeability obtained from AI technique. Table 1 shows the detailed database used in the current study.

Table 1 Detailed dataset
Full size table

Formation evaluation for the studied wells

Well log data were used to perform formation evaluation to obtain petrophysical parameters such as shale volume (Vsh), porosity (Ø), water saturation (Sw), reservoir, pay flags and the ratio between them. Shale volume is calculated by the linear formula (Eq. 1) from gamma-ray for a pessimistic estimation (Atlas 1979) and from density–neutron log (Eq. 2) (Schlumberger 1972, 2009). Porosity determination in the study is primarily obtained from density and neutron logs (Wyllie 1963; Asquith and Gibson 1982; Schlumberger 1972) (Eqs. 3–6). Water saturation derived from Archie equation (Archie 1942) (Eq. 7) and from Indonesian equation (Poupon and Leveaux 1971) (Eq. 8). For reservoir and pay flags, standard cutoffs for shale volumes (50%), porosity (10%) and water saturation (50%) were applied in order and sequentially (Darling 2005; Kassab et al. 2020; El-Din et al. 2013).

$${\text{VSH}}=\frac{{{\text{GR}}}_{{\text{log}}}-{{\text{GR}}}_{{\text{sand}}}}{{{\text{GR}}}_{{\text{shale}}}-{{\text{GR}}}_{{\text{sand}}}}$$
(1)
$${V}_{{\text{sh}}}=\frac{X1-X0}{X2-X0}$$
(2)

where

$$X0={{\text{NPHI}}}_{{\text{ma}}}$$
$$X1={{\text{NPHI}}+{\text{M}}1({\text{RHOB}}}_{{\text{ma}}}-{\text{RHOB}})$$
$$X2={{\text{NPHI}}}_{{\text{sh}}}+M1 ({{\text{RHOB}}}_{{\text{ma}}}-{{\text{RHOB}}}_{{\text{sh}}})$$
$${M}_{1}=\frac{{{\text{NPHI}}}_{{\text{fl}}}-{{\text{NPHI}}}_{{\text{ma}}}}{{{\text{RHOB}}}_{{\text{fl}}}-{{\text{RHOB}}}_{{\text{ma}}}}$$
$$\mathrm{\O }=\frac{{\rho }_{{\text{ma}}}-{\rho }_{{\text{log}}}}{{\rho }_{{\text{ma}}}-{\rho }_{{\text{fluid}}}}$$
(3)

where

Ø = formation porosity, fraction.

ρ_ma = density of the rock matrix, g/cm3

ρ_fluid = density of saturation fluid, g/cm3

ρ_log = density log reading (bulk density), g/cm3

$$\mathrm{\O }=\sqrt{\frac{{\varnothing }_{{\text{N}}}^{2}+{\varnothing }_{{\text{D}}}^{2}}{2}}$$
(4)
$${\varnothing }_{{\text{e}}}= {\varnothing }_{{\text{t}}}- {\varnothing }_{{\text{sh}}}{V}_{{\text{sh}}}$$
(5)
$${\varnothing }_{{\text{sh}}}= \frac{{\rho }_{{\text{ma}}}-{\rho }_{{\text{sh}}}}{{\rho }_{{\text{ma}}}-{\rho }_{{\text{fluid}}}}$$
(6)

where

\({\varnothing }_{{\text{e}}}\)= effective porosity.

\({\varnothing }_{{\text{t}}}\)= total porosity.

\({\varnothing }_{{\text{sh}}}\)= porosity of shale derived.

\({V}_{{\text{sh}}}\)= volume of shale at formation.

$${S}_{{\text{W}}}=\sqrt[n]{\frac{{R}_{{\text{W}}}}{{\varnothing }^{m} .{R}_{T}}}$$
(7)

where

\({S}_{{\text{W}}}\)= water saturation, fraction.

Ø = porosity, fraction.

\({R}_{{\text{W}}}\)= resistivity of formation water, ohm.m.

\({R}_{{\text{T}}}\)= resistivity of uninvaded formation, ohm.m.

m = cementation exponent.

n = saturation exponent.

$${{\text{SW}}}_{{\text{indo}}}= {\left\{\frac{\sqrt{\frac{1}{Rt}} }{\left(\frac{{{V}_{{\text{sh}}}}^{\left(1-0.5{V}_{{\text{sh}}}\right)}}{\sqrt{{R}_{{\text{sh}}}}}\right)+\sqrt{\frac{{\varnothing }^{m}}{a.{R}_{{\text{w}}}}}}\right\}}^{\left(2/n\right)}$$
(8)

where

\({{\text{SW}}}_{{\text{indo}}}\) = water saturation, fraction.

Rt = resistivity of uninvaded formation, ohm.m.

Rsh = resistivity of shale, ohm.m.

Vsh =volume of shale.

Ø = porosity, fraction.

a =Archie constant.

Rw = resistivity of formation water, ohm.m.

m = cementation exponent.

Rock typing/Clustering the formation

Core data were used to perform rock typing by reservoir quality index (RQI), the normalized porosity (Øz) and flow zone indicator (FZI) from the helium porosity and horizontal permeability measured using Amaefule formulas (Amaefule et al. 1993; El-Sayed et al. 2021; Abuhagaza et al. 2021; Kassab et al. 2021; Radwan et al. 2021a; El-Gendy et al. 2022; Ismail et al. 2023; Hassan et al. 2023) (Eqs. 9–11). The samples where then sorted in terms of FZI and grouped in rock types/clusters. Validation of the rock typing process by comparing permeability calculated from the actual FZI and the actual porosity from the core with the actual permeability measured from core.

$${\text{RQI}}=\text{0.0314}\sqrt{(\frac{k}{\O })}$$
(9)

Where

k is the horizontal permeability measured from core.

Ø is the porosity measured from core (preferably helium porosity).

Also, the normalized porosity (Øz) was calculated by the following equation.

$${\mathrm{\O }}_{z}=\frac{\mathrm{\O }}{(1-\mathrm{\O })}$$
(10)

Then, the flow zone indicator (FZI) was calculated by the following equation.

$${\text{FZI}}=\frac{{\text{RQI}}}{{\mathrm{\O }}_{{\text{z}}}}$$
(11)

Using machine-learning (ML) for rock type classification

In contrast with conventional programming methods, which typically involve creating a detailed design and implementing it as a program, ML takes a different approach. Instead of explicitly instructing the computer on how to solve a problem, ML algorithms learn from data and examples to generalize patterns and make informed predictions or decisions (Rebala et al. 2019). The process of machine-learning is divided into the following steps:

Feature engineering and data cleaning

Features is the terminology in machine-learning for the input data to the model, while labels are the terminology in machine-learning for the output data predicted or classified by the model. Features were conventional logs, while the label was the rock type.

Data cleaning was done by discovering and eliminating the plugs with bad test measurements (plug broken or test failure), nearly impermeable plugs (less than one md) and plugs where logs have problems while recording (noise while data acquisition), such as washout areas in the well where density and neutron log would give wrong readings for the formation.

Feature engineering was represented in the choice of conventional logs to be used in the machine-learning model, which was then decided, by choosing the gamma-ray (GR), density (RHOB), neutron (NPHI) and sonic (DT) logs. The resistivity log was excluded as it has no relationship to the facies, porosity or permeability of the formation as it is mainly related to the formation fluids and not the formation and its pore space, size and geometry due to the low to non-collinearity between these features.

These logs were scaled and normalized for each well by means of the min–max scaler (Dodge 2003; Freedman et al. 2020) (Eq. 12), which uses the following equation:

$${X}_{{\text{scaled}}}= \frac{(X-{X}_{{\text{min}}})}{({X}_{{\text{max}}}-{X}_{{\text{min}}})}$$
(12)

The standard scaler was excluded, as the data did not follow a Gaussian distribution, where the standard scaler performs better in such data. The scaling step is essential for the machine-learning model as most machine-learning algorithms are sensitive to the input values and could be biased toward big values and inputs with large scales (scale of GR curve ranges from 0 to 100, while RHOB curve ranges from 1.95 to 2.95) and deteriorate the machine-learning model.

Choosing the machine-learning algorithm

After examining the generalized buffering algorithm, which takes the distance geometrically along with the characteristics, attributes in regards (Zhou et al. 2021) and also examining the deep learning stochastic framework which aids in the subsurface structure estimation (Zhan et al. 2022). Core data and log data for each well were then concatenated by means of measured depth. Then, the data are split based on the wells, where OCT-A2B and OCT-B8 were the train data, i.e., the data from which the machine-learning algorithm will learn, and OCT-B6 was the test data, i.e., the data on which the machine-learning algorithm will apply what it learned. The following machine-learning algorithms were used for the data after the wrangling:

  1. 1.

    Random forest classifier (RF)

  2. 2.

    Extreme gradient boost classifier (XGB)

  3. 3.

    Multi-layer perceptron/neural network classifier (MLP/NN)

  4. 4.

    Support vector machine classifier (SVC) with radial-based function kernel (RBF)

  5. 5.

    Support vector machine classifier (SVC) with polynomial kernel

A range of hyper-parameters for each algorithm were used by iterations and observing the results and metrics such as the accuracy score (Eq. 13), precision score (Eq. 14), recall score (Eq. 15), F1 score (Eq. 16) and confusion matrix. The confusion matrix was the most important and effective metric, as it clarifies how each sample has been classified and what its classification result was (Powers 2020).

These metrics have the following equations:

$${\text{Accuracy}}= \frac{({\text{TP}}+{\text{TN}})}{\left({\text{TP}}+{\text{TN}}+{\text{FP}}+{\text{FN}}\right)}$$
(13)
$${\text{Precision}}= \frac{{\text{TP}}}{\left({\text{TP}}+{\text{FP}}\right)}$$
(14)
$${\text{Recall}}= \frac{{\text{TP}}}{\left({\text{TP}}+{\text{FN}}\right)}$$
(15)
$$F1-{\text{Score}}= \frac{(2({\text{Precision}})({\text{Recall}}))}{\left({\text{Precision}}+{\text{Recall}}\right)}$$
(16)

where TP, TN, FP and FN are true positive, true negative, false positive and false negative, respectively.

A true positive (TP) occurs when the model correctly predicts an instance as belonging to the positive class. It means the model identified a positive case correctly.

A true negative (TN) happens when the model correctly predicts an instance as belonging to the negative class. It means the model identified a negative case correctly.

On the other hand, a false positive (FP) occurs when the model incorrectly predicts an instance as belonging to the positive class when it is actually from the negative class. It means the model identified a negative case as positive.

A false negative (FN) happens when the model incorrectly predicts an instance as belonging to the negative class when it is actually from the positive class. It means the model identified a positive case as negative.

A true class is the event that the model is aiming to predict/classify while a negative class is any other possibility. In our case, one of the rock types will be the true class, while all the other rock types will be considered negative classes by the model. The best algorithm and hyper-parameters that produce the best accepted results shown by these metrics is extreme gradient boosting (XGB) (Chen and Guestrin 2016). XGB is a group of random forests, which is, in turn, a group of decision trees; it is a split-based algorithm to predict or classify the labels of a labeled dataset by means of the entropy and Gini index of the data after each split. Via minimizing the entropy and the Gini index to the least possible value as the dataset is well classified or predicted as the entropy and Gini index decrease. These trees and forests are a relatively weak predictor, and each tree and forest work sequentially, not in parallel. This is to pass the results of each weak predictor to the next weak predictor so that each consecutive predictor would learn from the errors of the previous predictor, thus minimizing the error and achieving the best results possible. The XGB is used with its default hyper-parameters except for Max_Depth, as the best value for it was ten instead of the default value of six.

Calculating permeability and validating the rock typing and machine-learning results

Permeability from rock types was calculated from the following Amaefule equation (Amaefule et al. 1993) (Eq. 17):

$$k=1014 {({\text{FZI}})}^{2} \frac{{\mathrm{\O }}_{{\text{e}}}^{3}}{{(1-{\mathrm{\O }}_{{\text{e}}})}^{2}}$$
(17)

where

k is the horizontal permeability.

FZI is the mean flow zone indicator.

Øe is the effective porosity.

Validation of the machine-learning model by comparing permeability calculated from predicted FZI and actual porosity from the core with the actual permeability measured from core, while validation of the predicted permeability curve by comparing permeability calculated from predicted FZI and calculated porosity from the logs with the actual permeability measured from core.

Dealing with missing data and calculating permeability from NMR log

Sonic log was absent in OCT-K5 well, this log is a necessary input/feature to the machine-learning model, therefore, it was synthesized using Gardner equation that links sonic log to density log (Gardner et al. 1974) (Eq. 18). The best empirically derived coefficients are found through iterations of sonic and density logs in numerous offset wells. The machine-learning model is then applied to the well, and permeability curve is calculated. Permeability from NMR log is calculated by Coates formula (Coates et al. 1999) (Eq. 19). Finally, permeability calculated from the machine-learning model is compared to that calculated from NMR log.

$$\rho = \alpha {V}_{p}^{\beta }$$
(18)

where

ρ is the density log in g/cm3.

Vp is the sonic log or P-wave velocity.

α is a formula empirically derived coefficient.

β is a formula empirically derived coefficient.

$$k = \left( {\frac{{\emptyset _{{{\text{NMR}}}} }}{C}} \right)^{4} \left( {\frac{{{\text{FFI}}}}{{{\text{BVI}}}}} \right)^{2}$$
(19)

where

k is the horizontal permeability.

C is a constant depending on lithology.

ØNMR is the porosity from NMR log (given from the log).

FFI is the free fluid index (given from the log).

BVI is bulk volume irreducible (given from the log).

Results and discussion

Formation evaluation results

Wells OCT-A2B and OCT-B6 have core electric parameters obtained from special core analysis (SCAL) such as cementation exponent (m), saturation exponent (n), Archie constant (a) and the formation water resistivity (Rw). Table 2 shows the results of the SCAL regarding the core electric parameters.

Table 2 Core electric parameters resulted from SCAL
Full size table

Formation evaluation is performed to estimate shale volume (Vsh), porosity (Ø), water saturation (Sw), gross reservoir, net pay thicknesses and net to gross ratio (N/G) for the Nubia formation to all wells. Core electric parameters for the wells with those parameters were used. While assumed default values per the Gulf of Suez Petroleum Company (GUPCO) were used for the wells with no core electric properties measured (OCT-B8 and OCT-K5). The values used for cementation exponent (m), saturation exponent (n), Archie constant (a) and the formation water resistivity (Rw) are 1.95, 2, 1 and 0.016, respectively. Table 3 shows the results of the average formation evaluation parameters. Figure 3 shows the formation evaluation for well OCT-B8. Figure 4 shows the same log and curves for well OCT-A2B.

Table 3 Average formation evaluation parameters
Full size table
Fig. 3
figure 3

OCT-B8 formation evaluation, the caliper log (CALI) and gamma-ray log (GR) are in the first track. Bulk density log (RHOB), neutron porosity log (NPHI) and bulk density correction log (DRHO) are in the second track. The deep resistivity log (RD) and medium resistivity log (RM) are in the third track. Sonic travel time log (DT) is in the fourth track. Bad hole flag (BHF) is in the fifth track, final shale volume (Vsh) is in the sixth track, final porosity (PHI_FINAL) is in the seventh track and Indonesian (final) water saturation (SWE_INDO) is in the eighth track. Finally, the reservoir net flag (RES_NET_FLAG) exists in the ninth track, and the pay net flag (PAY_NET_FLAG) is in the tenth track

Full size image
Fig. 4
figure 4

OCT-A2B formation evaluation, the caliper log (CALI) and gamma-ray log (GR) are in the first track. Bulk density log (RHOB), neutron porosity log (NPHI) and bulk density correction log (DRHO) are in the second track. The deep resistivity log (RD), deep induction resistivity log (ILD), medium resistivity log (RM) and medium induction resistivity log (ILM) are in the third track. Sonic travel time log (DT) is in the fourth track. Bad hole flag (BHF) is in the fifth track, final shale volume (Vsh) is in the sixth track, final porosity (PHI_FINAL) is in the seventh track and Indonesian (final) water saturation (SWE_INDO) is in the eighth track. Finally, the reservoir net flag (RES_NET_FLAG) exists in the ninth track, and the pay net flag (PAY_NET_FLAG) is in the tenth track

Full size image

Clustering and rock typing

After removing any impermeable core samples results, i.e., any samples with permeability less than 1 mD, 705 samples were obtained. Then, the rock quality index (RQI), normalized porosity (Øz) and flow zone indicator (FZI) are calculated.

These samples were then divided into five rock types or clusters by means of FZI. Table 4 shows the criteria for FZI ranges and mean FZI by which these rock types were classified and the mean FZI for each rock type. Figure 5 shows the samples after being rock typed.

Table 4 Criteria of FZI range and mean for rock typing
Full size table
Fig. 5
figure 5

Samples after rock typing

Full size image

To validate this clustering/rock typing process, the mean FZI for each rock type of each sample along with the helium porosity measured from the core is used to calculate permeability, and then, the calculated permeability by this method is plotted versus the measured permeability from the core in log–log scale. The R2 correlation coefficient was approximately 0.938, which is an almost identical correlation; therefore, the rock typing is valid. Figure 6 shows the measured permeability from the core versus the calculated permeability from the rock typing process.

Fig. 6
figure 6

Measured permeability versus calculated permeability

Full size image

Machine-learning process

Data cleaning and exploration

A filter on the core samples is applied where any point in the wells concerning the study that has a caliper log (CALI) reading equal to or greater than 9 inches (0.5 inches greater than the bit size as the bit size in all wells is 8.5 inches) is eliminated. This step aimed to remove any noisy readings with errors due to washout, as the density and neutron logs would mostly have incorrect readings due to their relatively shallow depth of investigation, which would result in readings that represent the drilling mud properties more than representing the formation properties. This step further reduced the number of samples from 705 to 623. The core samples were calibrated in depth to match that of logs via the core gamma-ray.

Feature engineering

To achieve the best inputs/features/logs to use for the machine-learning model, two approaches were applied to the log data. First, a physical approach to the data is used, which results in excluding the resistivity logs and caliper logs. The former is more concerned with the fluids inside the formation than the lithology and facies of the formation, while the latter has no meaning in terms of facies and lithology as it only gives an indication of the hole size, so there is no real information from it, and it has been limited only for the purpose of identifying washout intervals and eliminating their associated data.

Second approach was of mathematical and statistical nature, as correlation between the remaining logs (GR, RHOB, NPHI and DT) was examined to identify any features highly correlated with each other so that only one of the correlated features is chosen. This step aims to eliminate any duplication in the features, as the mathematical model would be biased toward features that are highly correlated and would highly influence its prediction/classification. Figure 7 shows a matrix heat map that shows the correlation between the features and each other and between the label/output, which is rock type (RT).

Fig. 7
figure 7

Correlation matrix heat map between the features

Full size image

It can be noticed that no feature is highly correlated with any other, whether positive or negative correlation. Therefore, all four features will be chosen to enter the model and are ready for scaling. In addition, it is noticeable that the number of features is relatively small, which establishes a simple low-dimension machine-learning model easy to use for prediction/classification.

Choosing the machine-learning algorithm

After scaling the features (log data), each curve in each well of the study is scaled separately as each curve has its own range, and each well has its own unique conditions regarding the hole condition, hole size and tool calibrations and corrections. The data are split into train data that the model will learn from and test data by which the model would be validated through applying and comparing the predicted/classified rock type results with the actual rock types. The splitting was with a ratio of 90% of the samples were train data (561 from 623 samples) and 10% were test data (61 from 623 samples). In terms of wells, the data of wells OCT-A2B and OCT-B8 were for training, while the OCT-B6 well was for testing.

Each algorithm had several trials with the data applying wide ranges for the values of their respective hyper-parameters, and the choosing process is based on the metrics and results. After these trials, Table 5 shows the best metrics and results of each algorithm used, and figures from Figs. 8, 9, 10, 11 and 12 demonstrate the confusion matrix of each of these algorithms used.

Table 5 Metric score and results of different algorithms
Full size table
Fig. 8
figure 8

MLP_NN confusion matrix

Full size image
Fig. 9
figure 9

RF confusion matrix

Full size image
Fig. 10
figure 10

SVC_Poly confusion matrix

Full size image
Fig. 11
figure 11

SVC_RBF confusion matrix

Full size image
Fig. 12
figure 12

XGB confusion matrix

Full size image

As noticed, most of the metrics of most of these algorithms are similar, but the decisive metric was the confusion matrix, as the confusion matrix of all the algorithms was predicting/classifying the rock types very skewed away from their actual rock types. Except for the extreme gradient boosting (XGB) algorithm, which although got a similar incorrect number of samples like the other algorithms yet what the algorithm classified incorrectly was not extremely skewed or far away from the actual rock type (mostly a difference of one rock type than the actual in either the negative or positive direction). This could be an accepted result, as rock types are not sharply separated and could show some sort of interference between each rock type and the one that precedes or succeeds it.

Therefore, the best algorithm chosen for this study was the XGB, and it was used with its default hyper-parameters except for “Max_Depth,” as the best value for it was ten instead of the default value of six.

In addition, it has been confirmed that the feature engineering and selection was successful, as all features contributed almost equally to the prediction/classification models. Figure 13 shows the feature importance of each feature to the model with the least important feature being RHOB with around 22% importance and the most important feature being NPHI with around 28% importance. The importance of the feature comes from how much it reduces the Gini index and the entropy of the data with each split regarding the feature.

Fig. 13
figure 13

XGB feature importance, NPHI feature has the highest importance of about 28% while RHOB feature has least importance of about 22%

Full size image

Calculating permeability

As mentioned previously, the mean FZI from the predicted/classified rock types along with the helium porosity from the core were used to calculate the permeability by the Amaefule equation then compared to the actual measured permeability from the core. This step is vital for the validation of the machine-learning model. The R2 correlation coefficient between the actual and calculated permeability was approximately 0.7281.

Then, the same step is done, but with the porosity calculated from the logs. This step is important due to the absence of core helium porosity in un-cored intervals and wells. The R2 correlation coefficient was approximately 0.51 (exactly 0.5098). The huge difference in the R2 correlation coefficient between estimating permeability based on helium core porosity and the same estimation based on porosity calculated from logs is not due to any defect in the machine-learning model. However, it is rather in the big difference between the helium core porosity and porosity calculated from logs, as in all cases, the same mean FZI is used in the equation, and in all cases, the same predicted/classified rock types are used. Figure 14 shows both steps and comparisons.

Fig. 14
figure 14

Measured permeability vs calculated permeability by core helium porosity (red) and measured permeability vs calculated permeability by porosity calculated from logs (blue)

Full size image

To prove that the decrease in the R2 correlation coefficient is due mainly to the porosity, another permeability was calculated using the mean FZI from the actual rock types and the porosity calculated from the logs, then compared to the actual permeability measured from the core. The R2 correlation coefficient reached over 0.66 (Exactly 0.6682). Figure 15 shows this comparison. Figure 16 shows a comparison between actual core measurements of porosity and horizontal and vertical permeability versus the calculated porosity from logs and the horizontal permeability predicted from a machine-learning algorithm.

Fig. 15
figure 15

Measured permeability vs calculated permeability by actual mean FZI and porosity calculated from logs

Full size image
Fig. 16
figure 16

OCT-A2B measured permeability versus predicted permeability, the core measurements of helium porosity (COPHI_SHIFT) along with effective porosity calculated from logs (PHIE_ND) in the first track, measured horizontal permeability from core (COHK_SHIFT) along with calculated permeability from the mean flow zone indicators (FZI) given from the predicted rock types through the machine-learning model (COHK_CALC) in the second track and the measured vertical permeability from core (COVK_SHIFT) in the third track for the well OCT-A2B

Full size image

Dealing with missing logs using Gardner equation

When attempting to apply the machine-learning model on the un-cored well OCT-K5, it was found that it has no sonic log, which is an essential input/feature to the machine-learning model. Therefore, Gardner equation was used to estimate the sonic log from the density log.

To obtain best α and β, many trials with the density log then comparing the calculated sonic log to the actual sonic log of the offset wells to the well OCT-K5, it was found that α = 0.2 and β = 3.1. The R2 correlation coefficient was approximately −0.71 (exactly −0.708), the negative correlation coefficient is due to the inverse relation between density (compactness of the formation) and sonic velocity (travel time).

NMR permeability versus estimated core permeability from rock typing

After the estimation of the sonic log by Gardner equation, the machine-learning model could be applied on the well OCT-K,5 and rock types of the Nubia formation in the well could be predicted/classified, from which permeability could be estimated similarly to the previous wells.

In addition, the NMR log run in the well is used to estimate permeability using Coates method/equation with the constant “C” value taken as 33 as this value is the correct value for sandstone, the dominant lithology in the formation.

Finally, the permeability estimates from both sources are compared to each other. The R2 correlation coefficient was approximately 0.48 (exactly 0.4755). The reduction in correlation coefficient and accuracy between this well and the other cored wells is due to the synthesizing of the sonic log, which, like any synthesizing process, leads to some error in the estimation.

Implications for petroleum exploration and development

Implications of obtaining a reliable continuous permeability curve in petroleum exploration and development could be summarized in the following points:

  • Aiding in the decision of perforation as it helps in choosing the most productive perforation intervals whether initial perforation or additional perforations within the well lifetime.

  • Supporting the secondary/enhanced recovery process as it provides information about the most likely paths where injected water would flow.

  • Reducing dependency on cores for acquiring reliable permeability data, which is more expensive, consumes more time, requires various procedures and tests that might fail and most crucial obtains permeability data in discrete points not continuously in the whole reservoir.

Limitations

Limitations of this study that could be avoided or mitigated in the future work and recommendations could be summarized in the following points:

  • Impermeable samples and almost impermeable samples were excluded from the rock typing process. Therefore, the machine-learning model did not learn such rock types which resulted in overestimating permeability when predicting permeability in impermeable intervals.

  • The machine-learning model was trained solely on the Nubia formation, different formations would need re-training of the model to achieve reliable accuracy.

  • Nubia formation consists mainly of sandstone; therefore, it is most unlikely for the model to predict rock types/permeability in carbonates with reliable accuracy.

  • Stacking of various, which is a method of ensemble machine-learning models, is likely to enhance the model results.

  • The machine-learning model aims to predict permeability in intervals where no cores are available. Thus, no helium porosity samples and only porosity calculated from logs is available; therefore, it is recommended when performing rock typing process to form the rock types using the porosity from logs as the permeability predicted will be calculated from this porosity, which differs than that of helium core porosity, combined with the flow zone indicator predicted from the machine-learning model.

Conclusions

The study could be concluded in the following points:

  • A simple and convenient machine-learning model is established using the commonly available four logs (i.e., gamma-ray, density, neutron and sonic), and reliable results are found regarding permeability prediction in the studied formation.

  • Consistent reliable performance of the machine-learning model is obtained as the accuracy of the model was negligibly reduced despite the deficiency of one of the input logs required (Sonic log), provided that it is properly synthesized.

  • Relationships between conventional logs and permeability have been obtained by means of machine-learning in the Nubia Formation, October Field, Gulf of Suez, Egypt.

  • To our knowledge, no similar machine-learning model has been established in terms of the convenience of the commonly available inputs required, the performance if one of the required inputs is synthesized and also in terms of the simple hyper-parameters of the algorithm used.