Introduction

Polycrystalline diamond compact (PDC) drill bits were introduced in the late 1970s as a means to increase rates of penetration (ROP) in soft to medium rock formations (Wang et al. 2019; Rostamsowlat et al. 2022) where roller cones failed to deliver sufficient performance. With drill bit performance affecting approximately 15–20% of the overall well cost (Okoli 2013), the industry turned to PDC bits. From a 15% market share in oil and gas drilling applications in the 90 s, PDC drill bits have reached a current 90% market penetration (Cheng et al. 2019). For a significant part, this evolution is due to improvements in the materials PDC drill bits are made of: primarily improvements in the impact and abrasion resistance of PDC cutters, but also improvements in the body material of the drill bit itself, whether tungsten-carbide or steel body bits (Bellin et al. 2010). These advances have allowed the industry to drill rock formations of higher rock strength or abrasiveness, and higher levels of vibration, impact and temperature. Parallel advances in the field of cutting structure design (Rahmani et al. 2021; Shao et al. 2022; Ke et al. 2023) have allowed to better balance loads on cutters to improve cutting efficiency, thus allowing gains in durability (Baker et al. 2010; Wei et al. 2022; Xiaofeng et al. 2022).

Depending on the drilling application, the rock cutting process shows a variety of experimental conditions in terms of cutting geometry, cutting kinematics, mud pressure within the well, pore pressure within the rock drilled, etc. Therefore, the rock cutting process has long been recognized as a cutting process evolving between a brittle regime (typically at high depth of cut, low cutting speed, low mud pressure or high pore pressure) and a ductile regime (typically at low depth of cut, high cutting speed, high mud pressure and low pore pressure) (Pelfrene 2010). In the brittle regime, larger fragments of cuttings are generated and cutting forces vary significantly, whereas in the ductile regime small cuttings or crushed rocks are generated and cutting forces vary much less (Richard et al. 1998; Zhang et al. 2022). Under such varying conditions, establishing cutter–rock interaction models to predict cutting forces from an a-priori knowledge of some fundamental rock properties is not straightforward. The literature of the rock cutting process indeed exhibits a wide range of choices when it comes to defining the so-called strength of the rock: rock strength has been specified either in terms of compressive, tensile (\(\sigma _t\)), shear or impact strength (Aadnøy and Looyeh 2019). Unconfined compressive strength (UCS) is the most widely used definition and physical quantity that researchers utilize for various applications (Gholami and Fakhari 2017; Al-Osta et al. 2018; Almisned and Alqahtani 2021). UCS is measured in atmospheric conditions (Morita 2021). In applications where in situ stress is applied (hydrostatic mud pressure while drilling), a better representation of the formation strength is given by the confined compressive strength (CCS) (Morita 2021). Uniaxial and triaxial compression tests are performed to obtain the UCS and CCS values and study a rock sample’s mechanical properties. Additional geomechanical properties are essential to characterize the rock behavior and research studies have shown that can be obtained by the drill cuttings (Li and Sakhaee-Pour 2018; Sakhaee-Pour and Li 2018; Esatyana et al. 2020).

Since it is not economically viable to conduct standard rock mechanics tests on core samples for every drilling application, researchers have developed laboratory tests to try to experimentally relate cutting forces to the above standard rock properties. At the drill bit scale, such tests are called drillability tests, whereas at the scale of one cutter, these are called single-cutter tests. Based on an extensive single-cutter experimental campaign, Adachi et al. (1996) and Richard et al. (1998) demonstrated that the uniaxial compressive strength of the rock can be correlated with the intrinsic specific energy of the rock cutting process. In the particular case where the cutter is sharp, the intrinsic specific energy of the rock cutting process is simply defined as the ratio between the tangential cutting force and the cutting area. These experimental results confirm the main assumptions of the cutter–rock interaction model developed by Detournay and Defourny (1992). In this model, cutter forces are decomposed into a cutting component and a frictional component to evaluate the response of sharp or blunt PDC cutter with respect to the intrinsic specific energy (\(\varepsilon\)) and the friction coefficient (\(\mu\)). These results have been confirmed by other authors (Schei et al. 2000; Richard et al. 2012), and the influence of the bottomhole and pore pressures have also been investigated (Zhou and Detournay 2014). Kalantari et al. (2019) developed an analytical model for a T-shaped drag bit, and experimentally investigated sharp and blunt cutters to estimate rock strength parameters and intrinsic specific energy. Ground investigations in geotechnical and mining operations are significantly important, and several methodologies have been proposed that assist in obtaining rock properties and rock characterization while drilling to improve safety and reduce cost (Rostami et al. 2015; Kumar et al. 2019; He et al. 2020; Wang et al. 2022). Therefore, the following sections address a new method to estimate the intrinsic specific energy while drilling.

Several different mechanistic and empirical models have been developed for the interaction between PDC cutters and the formation (Detournay and Atkinson 1991; Detournay and Defourny 1992; Gerbaud et al. 2006). Nevertheless, it is fair to state that there is at the current time no generally accepted method for determining rock strength from measurements of bit–rock interaction forces while drilling. Cutting forces increase linearly with the depth of cut (Detournay and Defourny 1992) up to a certain point, called founder point, where the efficiency of the cutting process decreases, and cutting forces then increase faster than the depth of cut. The depth of cut is also responsible for transition of the rock cutting regime from ductile, at low depths of cut, to brittle, at higher depths of cut (Richard et al. 1998, 2012). The back rake angle mainly controls how cutting forces are distributed between the normal component, mainly delivering the weight on bit (WOB) and the tangential component, mainly responsible for the torque on bit (TOB) (Rajabov et al. 2012; Rostamsowlat et al. 2018). Except for this purely geometrical effect, it has been shown that the back rake angle also intrinsically influences the rock cutting process, making it less efficient at higher back rake angles (Akbari 2014; Sheikhrezaei and Akbari 2019). On the contrary, in the range of values encountered in real drill bit applications, the side rake angle does not seem to have a significant influence on the rock cutting process efficiency, which may be utilized for improved bit design purposes (Rajabov et al. 2012; Pelfrene et al. 2019a). The kinematics of the rock cutting process has been recognized as being influential, too: whereas, the cutting speed has been studied in the laboratory both under dry (Pelfrene 2010) and pressurized conditions (Detournay and Atkinson 1991; Kollé 1993; Kolle 1996; Amri et al. 2016; Chen et al. 2019). Although physical mechanisms involved in dry and pressurized experiments differ significantly, studies lead to the same conclusion that cutting speed has a positive influence on cutting forces. Such a rate-dependent phenomenon has been observed in the field (Jain et al. 2011).

To have the most accurate estimate of the drill bit mechanical response, measurement subs positioned right above the drill bit have been developed (Desmette et al. 2005). Although such subs were less than 1 meter in length, they increased the length of the BHA, which is generally considered by directional drillers as a perturbation to the expected directional behavior of the BHA. Hence, these subs have disappeared and have been replaced by more compact technologies regrouped under the vocable of in-bit sensing (Bowler et al. 2016; Sugiura and Jones 2019). Many of them only embed accelerometers and gyrometers which are small and easy to pack and give valuable information about the drilling process but not a direct access to drilling forces and rock properties.

PDC cutter/bit sensing is a topic that has attracted significant interest in the industry. Vaughn et al. (2015) described a sensing device(s) integrated on the superhard layer and/or substrate to estimate the condition of the cutting tool. Zhan et al. (2021) presented various aspects of sensors incorporated into the cutter and drill bit body and methods to acquire the data while drilling. Recent advances in this field have allowed to add force measurements directly in the bit head (Kouzaiha et al. 2022). Such tools provide a way to accurately monitor drilling forces at the bit, thus providing an accurate estimate of drilling performance indicators and, consequently, a 1D representation of the rock strength along the drilled section.

This paper aims to unlock the potential of embedding in-cutter sensing technology to measure the time evolution of interaction forces at the cutter scale and estimate the rock strength while drilling. This study provides significant insights into the high-frequency force measurements on an individual PDC cutter that enables 3D rock strength reconstruction. A set of laboratory tests performed on a scaled drilling rig with synthetic gypsum samples are presented and the results are compared to rock strength tests obtained from independent mechanical tests.

Experimental setup

Description of sensor characteristics and placement on the scaled drill bit

The scaled drill bit has been specifically designed and manufactured to contain two removable PDC cutters with a diameter of 19 mm and a thickness of 8 mm (Fig. 1a). The thickness of their diamond table (black area in Fig. 1a), which is in contact with the rock is 2 mm. The cutters present a 20\(^\circ\) incidence angle with the rock (back rake angle) and 0 side orientation (side rake angle). The radial locations of the cutters are 9 and 16.3 mm from the center of the bit for the inner and the outer cutter, respectively. The overall bit diameter is approximately 53 mm. An additional cavity has been milled into the bit body, behind the inner cutter, to allow for the placement of the load cell. The sensor measures the load applied to the back of the cutter through a pointed-button shaped contact and its rated output is 2 mV/V with a maximum output force measurable of 445 N (100 lbf). The carbide substrate of the cutter (gray area in Fig. 1a) is not brazed to the bit body to allow for the full transfer of the force applied to the face of the cutter to the load cell. This is not a standard configuration in the PDC drill bit industry where the vast majority of the PDC cutters are brazed to the bit body to prevent losing cutters while drilling. However, this is not strictly required as demonstrated by the development of rolling PDC cutters which were introduced to let the PDC roll around its axis, thus allowing to uniformly distribute the wear across the entire cutter face (Zhang et al. 2013; Giumelli et al. 2014). In addition, airflow nozzles have been milled to evacuate cuttings produced during the drilling process. Figure 1b shows the scaled drill bit design from different angles.

Fig. 1
figure 1

a Scaled drill bit drawing with the placement of miniature load cell, b scaled drill bit design (red represents the miniature load cell)

Full size image

Scaled drilling rig

A scaled drilling rig and drill bit is used to estimate the rock strength during the actual drilling process. The capabilities of the scaled drilling rig are demonstrated in detail by Koulidis et al. (2021, 2022); Koulidis and Ahmed (2023). We analyze the acquired measurements from the scaled drill bit and the drilling rig to monitor the applied force on the PDC cutter. The depth of cut is accurately controlled with a closed loop DC motor-based hoisting system and the drillstring rotational speed with an AC motor. Continuous drilling requires control of the depth of cut, otherwise, motor stalling and excessive vibrations occur. An incremental rotary/shaft encoder signal measures the number of pulses per revolution and estimates the rotary speed of the DC motor. This method allows us to distinguish the downward movement and accurately calculates the actual and cumulative depth of cut at any data point. DC motor rotation starts before the drill bit touches the formation; thus, a constraint is applied to initiate elapsed time when the force sensor reading is greater than the starting condition.

When the drilling is initiated, the effective cutting area increases until it reaches the maximum DOC that the current scaled drill bit allows, corresponding to approximately 2.0 mm footage. Figure 2 illustrates the applied forces with respect to axial displacement. Since the sensor data dispersion is low, the mean value for specific drilled footage can be obtained accurately for every sample tested (Fig. 2). It can be observed that for all samples, at approximately 2.0 mm footage, the forces are stabilized due to the maximum cutting area that can be achieved for a constant axial displacement. The axial velocity for the conducted experiments in Fig. 2 is set to 0.2175 mm/s and drillstring rotational speed to 30 RPM.

Fig. 2
figure 2

The forces acting on a single cutter and the torque on bit. A more significant percentage of the total cutting force is transferred as a tangential component with the normal force to contribute minimum in the cutting process. At approximately 2.0 mm footage, the forces stabilize till the axial movement speed changes

Full size image

Since each sample has a different UCS, the evolution of the force acting on the face of the cutter is accurately captured while drilling. As described, the measured force’s projection in the tangential direction is utilized to calculate the intrinsic specific energy. It can be observed in Fig. 2 that from Sample 9, the variations of the force measured in the cutter have high data dispersion and might indicate a brittle failure mode. In addition, variations are amplified due to heterogeneities in the rock sample because experiments are conducted at atmospheric pressure, making the rock cutting process more brittle. Even though the signals from each sensor are processed similarly, the WOB and TOB signals are noisy compared to the in-cutter force sensor.

Data acquisition and control system

Analog and digital sensors are installed across the scaled drilling rig structure and equipment to collect the applied forces, torque and displacement data with a sampling frequency of 400 Hz. The following Fig. 3 illustrates the systems of the scaled drilling rig with respect to equipment and sensors.

Fig. 3
figure 3

Scaled drilling rig design and control system

Full size image

The VFD is controlled via a Modbus communication protocol with LabVIEW. LabVIEW provides a Modbus library that allows the serial communication of a Modbus device either when a request is made from the “master device” (PC) to the “slave device” (VFD) for acquiring information (frequency, module temperature, etc.) or to perform a requested action. The DC motor driver is connected with an Arduino Uno to control the direction and the rotational speed, followed by a Visa Serial to LabVIEW to control the Arduino buttons. The rotational speed of the drillstring is set to 30 RPM. With a sampling frequency of 400 Hz, 800 data points can be captured during one revolution of the inner cutter, corresponding to a traveling distance of 56 mm.

Bandwidth signal processing and electromagnetic interference

Because of the drillstring rotation, a slip ring is utilized to transmit the signal from the miniature load cell to the data acquisition system. Due to the discontinuation of the sensor cable at the slip ring, the EMI produced from the VFD interferes with the acquired analog signal from the miniature load cell. To reduce the effect of EMI prior to the signal being acquired by the data acquisition device, it is crucial to install an EMI filter (Fig. 3) connected to the AC power supply and the VFD. When the data is recorded, a low-pass filter with a cutoff frequency of 20 Hz is applied to reduce any additional noise from acquired signals. The combination of EMI filter and low-pass filter reduces the uncertainty of the signals used to evaluate the physical properties of the rock samples, thus enabling high-quality experiments. An algorithm to separate all the acquired data and conduct calculations every rotation is created to compute the active cutting area while drilling by considering the pre-cut groove.

Methodology

Sample preparation

In order to verify the results of the scaled drilling rig, it is important to test homogeneous and isotropic samples using established tests to obtain a reference value for the rock strength and the rock properties. It is common in civil engineering to create cement and concrete samples by placing the mixture in a mold followed by a specific curing procedure (C-31 2008). This work followed the same principle by creating four different molds, corresponding to four different tests (scaled drilling rig, scratch, uniaxial compression and Brazilian tests). Different rock properties, including rock strength, can be obtained by controlling the water to gypsum ratio. The dimensions for the uniaxial compression and Brazilian tests were followed per ASTM international standards (D4543-08 2008).

Rock properties

A total of 43 gypsum samples were manufactured to analyze the data from uniaxial, Brazilian, scratch and scaled drilling rig tests. The rock properties illustrated in Fig. 4 are compared with two additional gypsum samples by Papadopoulos et al. (1994) to investigate the validity of the tests. Since all the rock samples tested in the scaled drilling rig have an unconfined compressive strength of less than 10 MPa, the Brazilian test was performed on a few samples. For a sample with a plane of failure, it can assist in calculating the internal friction angle (\(\phi\)), and thus the cohesion (\(S_o\)). In contrast, for samples where the plane of failure is almost vertical, and since the \(\sigma _t\) and UCS are known, the internal friction angle can be calculated (Sivakugan et al. 2014) from Eq. (1):

$$\begin{aligned} \frac{UCS}{\sigma _{t}} = \frac{2(2 -\sin \phi )}{1 -\sin \phi } \quad \text {and}\quad \phi = {\sin ^{-1}}\frac{UCS-4\sigma _{t}}{UCS-2\sigma _{t}} \end{aligned}$$
(1)

The results show a linear increase of tensile strength with unconfined compressive strength and rock cohesion (Tugrul 2000; Vasarhelyi 2005) with \(R^2\) of 0.884 and 0.942, respectively. The friction angle values correspond to the range of 15\(^\circ\) to 30\(^\circ\).

Fig. 4
figure 4

Gypsum properties for the tested samples included online data (Papadopoulos et al. 1994)

Full size image

Rock strength determination from scratch test

The scratch test is a mechanical device that moves linearly and scratches a rock surface with a sharp rectangular PDC cutter at relatively low depths of cut, typically below 1 mm (Richard et al. 1998). Figure 5 illustrates the geometry of the test. During a test, both the tangential force (\(F_t\)) and the normal force (\(F_n\)) are measured. For each rock sample, a series of cutting passes must be performed to draw the evolution of the measured tangential force with the cutting area. For these tests, the PDC cutter speed was set to 20 mm/s, and the depth of cut was increased from 0.1 to 1.0 mm, with an increment of 0.1 mm.

Fig. 5
figure 5

Cross-sectional area for a sharp rectangular PDC cutter and the applied forces for linear motion

Full size image

As shown in Fig. 6, the tangential force is proportional to the cutting area which is expected since the PDC cutter used is sharp. In these conditions, the intrinsic specific energy is expected to directly match the UCS (Richard et al. 2012). It is also observed that the tangential force variations are lower compared to the scaled drilling rig measurements due to the linear movement across the sample surface and lower sampling frequency.

Note that if the PDC cutter would be chamfered, then according to Richard et al. (1998), the evolution of the tangential force with the cutting area would show a nonzero tangential force at zero cutting area. One would have to slightly modify the definition of the intrinsic specific energy, as shown in Eq. (2):

$$\begin{aligned} E = \frac{F_t}{A} \quad \text {and}\quad \epsilon = \frac{F_t\hbox {-intercept}}{A} \end{aligned}$$
(2)

This equation also accounts for the case where the cutter is sharp, in which case E = \(\varepsilon\).

Fig. 6
figure 6

Tangential and cutting area (left); tangential force measurements across the samples surface

Full size image

In the series of scratch tests performed, all data points with a depth of cut higher than 0.8 mm have been ignored since they clearly showed a transition from the ductile regime to the brittle failure mode.

Rock strength determination from scaled drilling rig

The interpretation of rock strength from the tests performed on the scaled drilling rig is done based on the same cutter–rock interaction model as the one used for the scratch tests, namely Detournay and Atkinson (1991). Just as for the scratch tests, PDC cutters used for the drilling rig tests are sharp and experiments are run under atmospheric conditions. The only difference with the scratch tests resides in the cylindrical-shaped PDC cutters used during the drilling rig tests. As observed in Pelfrene (2010), such a change in cutter shape should not significantly modify the results. Moreover, most of the existing analytical cutter–rock interaction models developed in the literature are bi-dimensional and are standardly applied to cylindrical-shaped cutters. Therefore, they relay this exact same assumption.

The tangential force is calculated with respect to the force acting on the sensor (\(F_s\)), which is normal to the cutter face, and the normal force (\(F_n\)) is measured with an additional load cell placed in the scaled drilling rig (Fig. 7). It is assumed that the WOB distributes evenly between the two cutters that the drill bit contains. Based on Detournay and Defourny (1992), the tangential component of the total cutting force is defined by Eq. (3):

$$\begin{aligned} F_{t} = \epsilon A \end{aligned}$$
(3)

The force measured from the load cell (\(F_s\)) is perpendicular to the cutter’s face. Therefore, it must be first decomposed into its three-dimensional components (\(F_t\), \(F_n\) and \(F_l\)) relative to the cutter’s frame (Fig. 7). These forces can be defined as in Eq. (4):

$$\begin{aligned} \begin{bmatrix} F_l \\ F_t \\ F_n \\ \end{bmatrix} = \begin{bmatrix} 0 \\ F_s \\ 0 \\ \end{bmatrix} \end{aligned}$$
(4)

For a sharp cutter, rotating the cutter by a back rake angle (\(\theta\)) in the \(u_t-u_n\) plane results in redefining the forces in Eq. (4), as shown in Eq. (5).

$$\begin{aligned} \begin{bmatrix} F_l \\ F_t \\ F_n \\ \end{bmatrix} = \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos \theta &{} -\sin \theta \\ 0 &{} \sin \theta &{} \cos \theta \\ \end{bmatrix} \begin{bmatrix} 0 \\ F_s \\ 0 \\ \end{bmatrix} \end{aligned}$$
(5)

Furthermore, by taking into consideration Eq. (5) and rotating the cutter by a side rake (\(\omega\)) angle in the \(u_l-u_t\) plane, the forces are further redefined as in Eq. (6).

$$\begin{aligned} \begin{bmatrix} F_l \\ F_t \\ F_n \\ \end{bmatrix} = \begin{bmatrix} \cos \omega &{} -\sin \omega &{} 0 \\ \sin \omega &{} \cos \omega &{} 0\\ 0 &{} 0 &{} 1 \\ \end{bmatrix} \begin{bmatrix} 0 \\ F_s\cos \theta \\ F_s\sin \theta \\ \end{bmatrix} \end{aligned}$$
(6)
Fig. 7
figure 7

Cutting forces acting on a sharp cutter. The miniature load cell (red) measures the force perpendicular to the cutter’s face

Full size image

Thus, the tangential force can be expressed as in Eq. (7), considering back rake and side rake angles.

$$\begin{aligned} F_{t} = F_s\cos \omega \sin \theta \end{aligned}$$
(7)

Experimental Results

Scaled drilling rig and scratch test comparison with the uniaxial compression

An extensive series of experiments are conducted to evaluate the capability of the proposed in-cutter sensing to estimate the rock strength while drilling. The interpretation of the rock strength in the helical sequence of the cutter and thus the mapping of the entire rock sample helps to monitor drilling performance and efficiency. It is thus important to make sure that the rock strength derived from the scaled drilling rig experiments is consistent with the rock strength evaluated through standard mechanical testing. Figure 8 compares the relationship between the intrinsic specific energy (\(\epsilon\)) and the uniaxial compressive strength (\(q\)) derived from the standard scratch test (left plot) and from the scaled drilling rig (right plot).

As already predicted by Detournay and Defourny (1992) and Richard et al. (1998), the intrinsic specific energy and the uniaxial compressive strength show a strong linear correlation (\(R^2=0.956\)) during scratch test experiments, which allows to use these values of the intrinsic specific energy as an indicator of the rock strength.

Results obtained with the scaled drilling rig (Fig. 8, right plot) show a similar strong linear correlation between the two quantities. The correlation coefficient is lower \(R^2=0.885\) than with scratch test experiments. This can be explained by the fact that the scratch test device is a very compact and stiff device working at very low cutting speeds (in the range of a mm/s), whereas the scaled drilling rig is designed as a slender structure subject to higher deformations and rotating at higher rotating speed, resulting in higher cutting speeds (in the range of a cm/s) and vibrations. Still, such a good correlation coefficient allows us to use values of the intrinsic specific energy derived from the scaled drilling rig experiments as an indicator of rock strength.

Fig. 8
figure 8

Scratch test (left); scaled drilling rig (right) Correlation of intrinsic specific energy (\(\varepsilon\)) and uniaxial compressive strength (q)

Full size image

3D mapping of sample rock strength

As the movement of the cutter sensor is prescribed and follows a simple helical path, it is possible to use measurements to map the estimated rock strength in 3D. As an example, the time evolution of the rock strength along this helical path for Sample 7 is shown in Fig. 9.

Fig. 9
figure 9

3D sample reconstruction based on rock strength. The helical sequence represents the trajectory of the cutter that the sensor is embedded. The uniaxial compressive strength is 3.7 MPa

Full size image

It can be observed that, after an initial phase at the top where the rock strength is higher, probably due to surface effects occurring while the slurry cured, rock strength values then stabilize around a steady-state regime. The histogram on the right side of Fig. 9 reveals a normal distribution of these values around an average value of 3.76 MPa. As expected from such a brittle and intermittent process as PDC rock cutting under atmospheric pressure, a notable standard deviation of 0.54 MPa and a noticeable negative skewness are also observed.

3D reconstruction of a bedding plane

To evaluate further the potential of mapping rock properties in 3D from in-cutter measurements, a heterogeneous sample of gypsum consisting of two layers of gypsum of different strengths separated by a bedding plane has been prepared and tested (Fig. 10). The hard gypsum mixture has been poured first into a mold inclined by an angle of 10\(^\circ\), measured with a standard digital inclinometer having a resolution of 0.1\(^\circ\). Uniaxial tests conducted on a sample of this harder mixture indicate a UCS of 4.6 MPa. Then, after setting the mold horizontally, the soft gypsum mixture has been poured. Uniaxial tests indicate a UCS of 1.8 MPa for this softer rock.

Fig. 10
figure 10

Formation layers and bedding plane

Full size image

The time evolution of the force recorded at the cutter (\(F_s\)) is represented in the top plot in Fig. 11. A low-pass filter with a cutoff frequency of 40 Hz has been applied to denoise the raw signal sampled at 400 Hz. Three distinct phases can be observed in this test. During phase 1, from about 20 to 63 s, although intermittent by nature, the force signal is relatively stable (showing an average, \(\overline{F_s}\) = 9.5 N and a standard deviation, \(\hat{F_s}\) = 2.2 N). This phase clearly corresponds to the cutter sampling the softer rock. During phase 2, from about 63 to 86 s, the cutter is transitioning to the harder rock (\(\overline{F_s}\) = 13.5 N, \(\hat{F_s}\) = 5.2 N). During phase 3, from 86 s to the end of the test, the cutter samples the harder rock (\(\overline{F_s}\) = 19.5 N, \(\hat{F_s}\) = 2.4 N). This signal has been processed to detect local extrema. From these extrema, both the sequences of increases (from a minimum to a maximum) and decreases (from a maximum to a minimum) have been detected and computed. The bottom plot in Fig. 11 shows the sequence of decreases in \(F_s\). The distinction between the three phases described above can thus be quantified through the use of the negative dispersion \(|F_{s,min} - F_{s,max}|\). Note that the sequence of increases (positive dispersion) shows a similar pattern.

Fig. 11
figure 11

Processing of the cutter force (\(F_s\)) time signal

Full size image

In both plots of Fig. 11, black dots values along the x-axis indicate the time when the negative dispersion was the highest. These have been selected by looking for values of the negative dispersion above a given threshold so that they could be considered as out of the probable range of values of the dispersion observed during phases 1 and 3, where the cutter drilled homogeneous rocks. Selecting the highest values of the negative dispersion is compatible with the idea of an intense stress relief occurring while the cutter leaves the hard rock to enter back into the soft rock. For each detected value above the threshold, the time when \(F_s\) was half-way between \(F_{s,max}\) and \(F_{s,min}\) (black dots values along the y-axis on the top plot of Fig. 11) was picked. Then, a plane was fitted against the point cloud formed by the values of x, y and z coordinates at these times (Fig. 12). The plane was determined following a principal component analysis that sets the normal to the plane (shown in Fig. 12) as the eigenvector corresponding to the lowest eigenvalue of the covariance matrix of the point cloud. A sensitivity analysis was conducted on the value of the threshold to verify the robustness of the procedure. The threshold was defined as the average of the negative dispersion over phases 1 and 3, plus \(n\) times its standard deviation. The sensitivity analysis shows that the optimum is obtained for \(n = 7.0\) with a standard deviation of the distance of the points to the plane of 0.44 mm. At this optimum, the plane has an inclination of 9.5\(^\circ\) and an azimuth of 126.7\(^\circ\), counted anti-clockwise from the x-axis. The inclination value matches well with the prescribed 10±0.1\(^\circ\), the difference being due to both the uncertainty in the pouring and the curing of the gypsum mixture and the assumptions made for the processing of the time signals. Although the azimuth of the plane was not monitored accurately during the tests, it is believed that this technology also has the capability to estimate it, provided that the angle of rotation of the drill bit can be tracked.

Fig. 12
figure 12

3D reconstruction of the bedding plane

Full size image

Similarly to the results presented with homogeneous samples, the evolution of the rock strength can be represented in 3D along the path of the cutter (Fig. 13). The transition from the lower strength rock at the top to the higher strength rock is clearly marked by the shift in rock strength values.

Fig. 13
figure 13

3D mapping of bedding plane and rock strength

Full size image

Benefits of in-cutter measurements over in-bit measurements

It has been shown that in-cutter measurements brought two major results: detecting changes in lithology and mapping these changes in the 3D space. In-bit measurements have long been used to detect changes in lithology. But they are unable to map them in the 3D space. This is illustrated in Fig. 14a where the time evolution of the force on the cutter and the rock strength (Fig. 13), both derived from in-cutter measurements of the current study, are compared to the weight on bit. The transition from the soft rock to the hard rock with in-cutter measurements is much more resolved in frequency and amplitude with in-cutter measurements.

Fig. 14
figure 14

a Applied forces while drilling layer 1, interface area and layer 2. b Forces acting on a bit cutter for a harder rock sample with constant axial speed

Full size image

Moreover, in-bit measurements can be parasited by phenomena that are unrelated to the rock cutting process. These can be frictional forces produced by contacts between the drillbit body or gages and the borehole wall. These can also be contact forces that arise from the drillbit engaging the rock with a very high DOC, so that non-cutting parts of the bit face (e.g., contact elements, blade tops) touch the bottom of the hole (Pelfrene et al. 2019b). Figure 14b illustrates such a scenario. This test was performed in a homogeneous sample. It can be observed that the WOB signal significantly increases around 20 s while the force on the cutter remains low. It is the result of the bit body contacting the formation while the DOC was higher than the cutter clearance which is 2 mm. Consequently, an additional non-cutting force was applied on the bit body and was recorded by the WOB sensor, but not detected by the in-cutter sensor since the cutter was engaged at its maximum DOC. This highlights the fact that in-cutter sensors can be considered as the recording devices allowing to monitor the rock cutting process with the highest resolution. As such, it complements in-bit sensors that are affected by a variety of phenomena in their goal to monitor drilling efficiency to safely and reliably conduct drilling operations.

Discussion

Integrating a force sensor behind the cutter to measure the applied force and estimate the rock strength is an innovative method that shows promising results. The first segment of the results has demonstrated that high-frequency measurements at the cutter enable monitoring of the force at the cutter and allow the estimation of rock strength while drilling. As it is described, the increase of the force perpendicular to cutter’s face is a function of the depth of cut and reaches a steady-state condition at approximately 2.0 mm footage of axial displacement. The fluctuations of the measured forces are induced by the brittle nature of the rock cutting process itself, but also by inevitable heterogeneities in the gypsum samples. Figure 15 illustrates that as the rock strength increases, the standard deviation from the mean value is significantly higher. The force sensor at the cutter can capture the increasing trend in applied force while drilling samples of different UCS. The evidence of the results has been compared to the other mechanical tests, including UCS and scratch, which confirms the fidelity of the in-cutter sensing technology.

Fig. 15
figure 15

Data distribution of the measured force at the cutter for samples with different rock strength

Full size image

The experiments described in this paper provide new insights into the reconstruction of the rock strength from cutter forces, at the drilling stage in a three-dimensional framework. The manufactured bedding plane separating two rock layers of different strength can be detected with accuracy. The cutter force signal helps monitoring when the cutter is actually drilling in the upper layer, when it crosses the interface, and starts drilling into the lower layer. While drilling the interface, it can be observed that the force on the cutter decreases significantly, and the other measurements (WOB and TOB) remain constant. The main reason behind this might be that the two layers are not completely attached, and it demonstrates the sensitivity of the in-cutter sensing compared to other measurements. Moreover, the in-cutter force measurements provide information on the evolution of the cutting process and can distinguish between partial engagements of the drill bit with the formation and evaluate the actual weight on bit which is distributed at the cutter.

Despite the promising results of the current study, several limitations can be raised concerning the feasibility of the in-cutter sensing technology. These include (i) experiments are conducted with very low strength synthetic rocks, (ii) the effect of the drilling fluid is not considered, (iii) neither the effect of cutter chamfers nor cutter wear are not considered. Additionally, motor stalling can occur while drilling the rock sample due to induced vibrations. To accurately assess hard rocks, the depth of cut per revolution must be reduced. This is accomplished by increasing the drillstring rotational speed, albeit compromising the resolution.

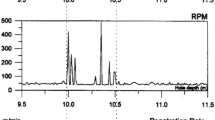
Two main factors affect the spatial resolution of the experimental work: the rotational speed and the sampling frequency. The sampling frequency is limited due to data acquisition from multiple analog and digital sensors. To evaluate the effect of the rotational speed, an additional test has been conducted with a rock sample where a vertical cavity has been pre-drilled across the path of the inner cutter where the load cell is installed (Fig. 16a). As observed in (Fig. 16b), at a low rotational speed of 30 RPM, there is a sharp drop in cutting force when the cutter enters the cavity. This phenomenon repeats itself for every revolution. However, when the rotational speed is increased to 90 RPM, since the axial speed is fixed, the depth of cut is reduced by a factor 3 and it can be observed that the drop in cutting force is not well resolved anymore. This spatial variability and the necessity of high-frequency measurements can be utilized while drilling vuggy carbonates and shale formation to evaluate the bedding plane and identify formation tops.

Fig. 16
figure 16

a Graphical illustration of the cutting process, b spatial monitoring of the applied force at the cutter while drilling a rock sample with different rotational speeds

Full size image

Conclusions

This work investigates the rock cutting process by PDC cutters based on an extensive experimental campaign conducted on a laboratory-scale drilling rig, using a two-cutter drillbit, and drilling into samples of synthetic low strength rocks made of a gypsum mixture. The design and the implementation of a novel in-cutter force sensing technology are also presented. It allows to monitor the time evolution of drilling forces along the path followed by the cutter. Based on a standard cutter–rock interaction model, the drilling force measured at the cutter can be used to estimate the rock strength 3D spatial distribution.

Two series of drilling tests have been conducted to evaluate the potential of this technology.

  • First, homogeneous rock samples have been prepared to evaluate the ability of the system to estimate the sample rock strength with accuracy. Results show a strong linear relationship (\(R^2=0.885\)) between the intrinsic specific energy derived from the scaled drilling rig experiments and the rock strength obtained from uniaxial compression tests.

  • Second, heterogeneous rock samples have been prepared and tested following the same experimental protocol. These samples consisted of two layers of gypsum mixture separated by a bedding plane with a dip angle of 10\(^\circ\). The 3D spatial distribution of the rock strength has been estimated and the geometry of the bedding plane has been reconstructed, resulting in a fair estimation of the dip angle of 9.5\(^\circ\).

These experimental results indicate that the in-cutter sensing technology can provide valuable information on 3D mechanical rock properties, including heterogeneity and anisotropy. Although the in-cutter sensing technology presented is still at an early stage of development, it is believed that recent advances in the field of embedded compact measuring and recording devices would help in manufacturing a full-size prototype able to withstand drilling tests with harder rock formations. Under this assumption, this technology would provide the geoscientist a new way of investigating complex lithological structures at an early stage of the field exploration or development, thus nicely complementing coring and logging operations that are expensive and time-consuming.