Introduction

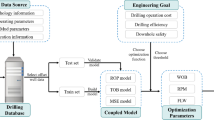
Hydrocarbons are formed on earth’s subsurface by the decomposition of organic sediments deposited several millions of years ago. Upon increasing burial with depth, it becomes subjected to increasing temperature and pressure forming kerogen which later produces hydrocarbons within the pore spaces of the rock. A rock material is a naturally occurring aggregate of minerals, constituting an important part of earth crust. According to Emery (1966), a rock is defined as a composition of granular material and glue. Formation rock is a heterogeneous and anisotropic material and therefore a complex material to study from the mechanical viewpoint (Alfreds 1983). One of the most used classification of rocks is based on their origin, which classified rocks into three types of igneous, sedimentary, and metamorphic rocks Alfreds (1983). Hydrocarbons are commonly found in sedimentary rocks enclosed within a geologic trap. Drilling a borehole is the only way to harness the hydrocarbon deposited several thousands of feet beneath the subsurface. In oil-well drilling, the process involves creating a borehole achieved by simultaneous rotary action of the topdrive and the application of axial force by the drawwork hoist, wherein the former transmits torque to the drill bit via the drill string, and the latter facilitates drill string longitudinal motion, thereby establishing drill bit normal force commonly referred to as weight on bit (WOB) (Akgun 2002). During the drilling operation, the drill bit cuts the rock material and the resulting drill cuttings are removed from the borehole by the circulation of drilling fluid which is pumped into a well through the rotary hose and drill string; Fig. 1 shows the schematic of a topdrive rotary drilling rig.

Fig. 1
figure 1

Schematic of a topdrive rotary drilling rig with bottom-hole assembly (BHA) (Šprljan et al. 2020)

Full size image

There are two main modes of rotary drilling system: manual drilling and autonomous drilling system. The traditional manual mode of drilling system is manned by the driller who controls the rotary action of the topdrive and the axial force of the drawwork. The driller determines the operating parameters either by intuition, previous experience, or by trial-and-error approach. Alternatively, the autonomous rotary drilling system is designed to reduce mental and physical workload of human operator. There are several other benefits that could be derived from autonomous drilling system including efficiency, health, safety and environmental factors. First, automation responds faster to problems with fast and small corrections versus large corrections or costly remedial actions of conventional system. Also, autonomous drilling system will offer a step change in downhole monitoring of drilling conditions improving operation safety. Economic benefits emanate from operating closer to constraints and reducing well delivery time and cost and improve operational health and safety by elevating the driller from direct involvement in the drilling operation into a supervisory role, thereby eliminating the trial-and-error methods which in turn improve efficiency in terms of manpower and operational cost. This research supports the initiative in modelling and optimizing rate of penetration (ROP) of an autonomous rotary drilling system using predictive data-driven (PDM) modelling.

Literature review

The drive to optimize oil and gas portfolios through automation dates backs to the late 90’s. According to Norwegian Oil Industry Association (2006), Norway Scientific Council and Statoil developed a program called integrated operation to take the advantage of exploiting deeper subsea fields under a new information and communication technology program. Autonomous drilling system consists of three parts: the real-time monitoring, decision-making, and actuator as presented in Amadi et al. (2022). The real-time monitoring provides the environmental information for decision-making and control execution. Amer et al. (2017) used the application of control system and information technology to operate both the topdrive and the drawwork system. McKenna et al. (2015). Chiranth et al. (2017) discussed the different established drilling models, which were classified into two groups: physics-based models and data-driven models.

The physics-based empirical models are commonly used in ROP prediction (Soares et al. 2016) including Graham and Muench model, Maurer model, Maurer (1962), Bingham model, Bingham (1965), Warren model, Warren (1987), Bourgoyne and Young model. Bourgoyne and Young (1974), Soares and Gray (2019) showed the disadvantages of the physics-based models, which includes the use of empirical constants such as the bit design constants, mud properties and formation constants, as well as low prediction, accuracy and their conformality to a homogenous formation. In contrast to the physics-based model, the contemporary data-driven models used the surface drilling parameters such as the weight on bit (WOB), rotary speed (RPM) and flowrate to predict ROP, Khoukhi and Ibrahim (2012). The implementation of the data-driven model overcame the limitations of the traditional physics-based models making optimization task less complex. Mckenna et al. (2015) investigated the concept of a search logic optimizer to emulate experienced human controller using a typical “hill-climber” algorithm in a statistical model (Buntine 1992) for formation drilled whilst optimizing the setpoint combinations. However, it was reported that the primary challenge to the stochastic modelling systems was the non-homogeneity and the continuous change in the formation being drilled Hedge et al. (2015).

Bilgesu et al. (2017) tested the technology of neural network with the data-driven models to predict ROP and bit wear with different operating parameters. In their study, nine input parameters were used and result achieved a correlation coefficient (R2) that ranged from (0.902 to 0.982). A similar study was conducted by Moran et al. (2010), using artificial neural network (ANN) to predict ROP with six input parameters including RPM, WOB, mud weight, rock strength, abrasion, and rock type from offset well data. The ROP prediction attained a coefficient of determination of R2 value of 0.8. Manshad et al. (2017) created a multilayer ANN to model ROP with genetic algorithm (GA) with 332 datapoints and ten input parameters. Several other investigators including Jiang and Samuel (2016); Bhowmik et al. (2017); Arabjamaloei and Shadizadeh, (2011); Bataee and Mohseni (2011) and Manshad et al. (2017) have used ANN to predict ROP with five to ten input parameters. Table 1 shows the summary of penetration rate models and their respective model performance parameters.

Table 1 Summary of penetration rate models
Full size table

Ahmed et al. (2019) performed a ranking of the 19 input parameters used in predicting ROP from the various studies based on parameters with the greatest influence on ROP using the feature extraction rule, which is used to evaluate the effect of input drilling parameters on ROP as shown in Fig. 2. The analysis showed that WOB, RPM and flow rate were the first, second and third most influencing factors. The application of machine learning (ML) for ROP prediction is widely supported by many researchers; out of the 53 reviewed works, 47% of the researchers used ANN followed by the Ensemble at 15% and SVR at 12% as shown in Fig. 3.

Fig. 2
figure 2

Frequency of input variables used in ROP prediction

Full size image
Fig. 3
figure 3

Distribution of researchers and machine learning methods

Full size image

Data and methods

This section presents the procedures used in preparing dataset; it shows the defined input–output data relationship using a graphical representation. In addition, calculation of the derived controllable variables using appropriate established correlation and finally steps used in ANNs modelling and sensitivity studies were presented. Well-P05 has a total of 246 datapoints from 7400 to 10630 ft measured depth. The following drilling surface parameters were collated: weight on bit (WOB), rotary speed (RPM), torque (Tor) and penetration rate (ROP) as shown in Table 2.

Table 2 List of drilling mechanics data used for this study
Full size table

Data gathering and reprocessing

Data collection and quality checks were the most challenging and time-consuming process in the study. During the study actual field drilling mechanics data from already drilled well, well-P05 was collected and resampled at 30-ft interval to reduce the data density as the data acquisition was done at every 0.5ft. This was done to check the influence of lesser data density on the accuracy of the prediction. Table 3 shows the summary of the statistics of the data.

Table 3 Range of input parameters and statistics (Dataset-P05)
Full size table

Calculation of derived controllable variables.

The calculation of derived controllable variables was performed using established empirical relationship that relates the penetration rate with the derived input variables. A brief description of the derived variables and their empirical relationship is presented.

Feed thrust (FET)

This represents the force that keeps the drill bit in contact with the formation. This is controlled by the distance of drilling line released by the drawwork hoisting system. It is a representation of the weight on bit (WOB) or axial thrust force. Equation (1) used to calculate feed thrust force (FET) was derived from earlier work of Lindqvis (1982) on the indentation force of hemispherical carbide buttons in rock and discussed in Cavanaugh et al (2008)

$${\text{FET}} = \frac{{1.5 *{\text{Tor}}}}{{{\text{Dia}}}}\frac{\varphi - 2v}{{\sqrt ( \varphi v - v^{2} )}}$$
(1)

where FET is feed thrust force (klbs), Tor is surface torque (Kft.lbs), \(\nu\) is cutter radius (in), \(\varphi\) is penetration rate per revolution (ft), Dia is drill bit or hole diameter (in) and RPM is revolution per minute.

Drilling mechanical specific energy (DMSE)

The concept of drilling mechanical specific energy was first introduced by Teale (1965), defined as the amount of energy required to destroy a unit volume of rock. Equation (2) is the mathematical relationship for DMSE in oilfield units. The DMSE is a representation of the energy from topdrive.

$${\text{DMSE}} = \left( {\frac{{480 *{\text{TOR *RPM}}}}{{{\text{Dia}}^{2} *{\text{ ROP}}}} + \frac{{4 *{\text{WOB}}}}{{\pi * {\text{Dia}}^{2} }}} \right) \times {\text{ Bit factor}}$$
(2)

where DMSE is drilling mechanical specific energy (Kpsi), Tor is surface torque (Kft.lbs), RPM is revolution per minute, bit factor is 0.125 for PDC bit and 0.25 for roller cone bit, WOB is weight on bit (klbs), ROP is rate of penetration (ft/hr), and Dia = hole diameter (in),

Figure 4 shows the graphical presentation of the data points from well-P05 showing the effect of the respective tuning parameters on ROP. An explicit relationship is observed with the derived variable as seen in tracks [C&D].

Fig. 4
figure 4

Plot showing relationship between the selected tuning parameters with ROP A SWOB versus ROP B RPM versus ROP C FET versus ROP and D DMSE versus ROP for Dataset of Well P05

Full size image

In track D, an inverse relationship is observed between DMSE and ROP, whilst in track C, a direct relationship is observed between FET and ROP. No explicit relation was observed in track A and track B.

Statistical analyses

The influence of the input surface drilling parameters on ROP (output) in the drilling system was studied by performing statistical analysis of the dataset. The statistical analysis was useful in identifying outliers (data outside the acceptable limits) which were subsequently deleted from the dataset. Table 3 shows summary of input parameters for well-P05. Understanding the relationship between the input and output variables is of primary importance when developing ANN models.

Artificial neural networks

ANNs are information processing structures that are universal function approximator and simplify simulation of a biological learning process with performance features like those of biological neural networks. Neural network consists of groups of nodes, or artificial neurons, that are linked in a way that allows them to be a universal function approximator, which means that given the right combination of nodes and connections, ANNs can simulate any input and output relationship. This is because they are adaptive, parallel information processing systems, which can build associations and mappings between objects or data and have been proven in solving problems in automation and pattern recognition Shadizadeh et al (2010). A multilayer perceptron (MLP) network can learn the behaviour and trends of earlier events with valid dataset. Therefore, the quality and accuracy of the datasets are very crucial in the accuracy of the prediction and subsequent decisions made by the ANNs technique. The processing elements of ANNs are artificial neurons. These neurons consist of four basic components that include input data (xf), connection lengths (wf), a transfer function (vf), and output value (y) (Ahmed et al 2019) as shown in Fig. 5

Fig. 5
figure 5

ANNs structure with 2 hidden layers showing input data (xf), transfer function (vf), and output value (y)

Full size image

Artificial neural networks configuration

Artificial neutral networks (ANNs) are interconnected in multilayer network topology that comprise three layers: (1) input layer, (2) one or more hidden layers, and (3) an output layer as shown in Fig. 5. The hidden layer(s) are the coefficients that provide the relationship between the input and output layers. The most common types of ANNs are feed-forward networks, which are the most efficient ones Abbas et al (2018). In the feed-forward ANNs structure, the information will transmit in one direction from input neurons through the transfer function of the hidden neurons to the outputs. Depending on the relative contribution of each unit in the hidden layer to produce the original output, these units will receive only a fraction of the total error signal. The neurons use transfer functions to create their output from the network input. The most used transfer functions are the PURELIN, TANSIG, and LOGSIG. The number of neurons in the input layer is equal to the number of parameters being fed into the network as input and vice versa for the target layer. However, a variation of neutrons in the hidden layers was used in the optimization and detailed discussed provided in the sensitivity analysis section below. Furthermore, the parameters used in the ANN modelling are summarized in Table 4. The model was built using ANNs with two neurons in the input layer and only one neuron in the output layer, the optimized number of thirty (30) neutrons. Different hidden layers of varying numbers of neurons were simulated with the PURELIN transfer functions, whilst the output layer was one neuron. The optimum number of neurons and layers was selected based on an iterative process by performing sensitivity analysis on the number of neutrons that provide the highest accuracy with respect to correlation coefficient (R2) as recommended by Haykin and Hakin (1998). In the modelling process, the database was randomly divided into two parts: A training dataset was used to develop and adjust the weights in a network, whilst the testing dataset was applied to examine the final performance of the ANNs. A 70:30 ratio was used for training and testing, respectively, as recommended in literature as more datapoint is required for training the model.

Table 4 ANN modeling and tuning parameters
Full size table

ANNs Simulation Cases.

Two simulation cases were studied, the first case “Case 1” was with input variables of WOB and RPM and ROP as the single output variable. However, in “Case 2” the input variables were DMSE and FET with ROP as the single output parameter. To effectively compare the performance of the input variables in ROP prediction, the same ANNs network configuration, number of hidden layers and transfer function were used in the scenarios modelling.

ANNs model performance assessment criteria

The criteria applied for assessing performance of the two cases are the three commonly used in engineering analysis benchmark to align with the best practice. The predicted performances of neural network models were assessed by correlation coefficient (R2), root mean square error (RMSE), and absolute average percentage error (AAPE).

Correlation coefficient (R2) is a measure of the similarity between the actual and the predicted values. The range of value of (R2) varies between 0 and 1. Whilst the value of 0 suggests no similarity, 1 signifies an excellent correlation between the model output and the actual predicted values. It is mathematically expressed using Eq. (3):

$$R^{2} = 1 - \frac{{ \mathop \sum \nolimits_{i = 1}^{n} \left( {f\left( {xi} \right) - yi} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} f\left( {xi} \right)^{2} - \mathop \sum \nolimits_{i = 1}^{n} f\frac{{\left( {yi} \right)^{2} }}{n}}}$$
(3)

where yi presents actual data, f(xi) is the predicted data, xi are the input parameters, and n is the total number of records. The higher R2 shows a close approximation between the actual and predicted values. The range of value of (R2) varies between 0 and 1. Whilst the value of 0 suggests no similarity, 1 signifies an excellent correlation between the model output and the actual predicted values.

The root means square error (RMSE) is a measure of error between the actual and the predicted values. It is used as an error function for the quality evaluation of the model. It is mathematically expressed in Eq. (4);

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {f\left( {xi} \right) - yi} \right)^{2} }$$
(4)

The average absolute percentage error (AAPE) is a statistical measure of the relative accuracy of the model prediction expressed in percentage. It can be calculated as the ratio of the mean of the absolute error as shown in Eq. (5)

$${\text{AAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {\frac{{/xi - yi/^{.} }}{xi}} \right]*100$$
(5)

Methodology

As illustrated in Fig. 7, a step-wise procedure is used in evaluating tuning functionality for autonomous system. Two options investigated include [WOB, RPM] and [DMSE, FET]. All the steps of the methodology were coded in the MATLAB version R2019a. The steps include:

Step 1: Calculation of the derived controllable variables

The feed thrust (FET) and drilling mechanical specific energy (DMSE) were computed using Eqs. (1 and 2), respectively.

Step 2: Statistics and graphical analysis was performed to identify and eliminate outliers from the dataset

Step 3: The dataset was divided in the ratio of 70:30 for training and testing, respectively. A total of 246 datapoints were used for well-P05 and 4185 datapoints for well-W1

Step 4: The ANN model was constructed with input layer, one hidden layer and the output layer. The number of neutrons in the hidden layer was varied in the sensitivity analysis to optimize the model result. Figure 6 shows the model configuration

Fig. 6
figure 6

ANN configuration with two input and an output variable

Full size image

Results

The summary of results of the step-wise procedure shown in Fig. 7 for ROP prediction using the actual surface parameters (ASP) and derived controllable parameters (DCP) for well P05 is shown in Table 5.

Fig. 7
figure 7

Research flowchart showing the step-by-step approach

Full size image
Table 5 Summary of the quantitative prediction and accuracy
Full size table

Result of prediction using actual surface parameter (Case 1):

The application of two actual surface parameters: (i) the weight on bit (WOB) and (ii) rotary speed (RPM) to predict the actual measured ROP obtained during the drilling process is presented in Fig. 8. The input data gave a poor prediction with R2 values of 0.74, RMSE of 28, and AAPE of 106. The cross-plot of actual measured ROP versus predicted ROP (a), the error distribution curve (b), and the comparison of actual versus predicted plotted along depth (c) are presented in Fig. 8, whilst samples of numerical values comparison of the actual measured ROP and the ANN predicted values are presented in Table 6. This result revealed that as the value of weight on bit increases, the value of ROP increases and vice versa. However, the overall prediction accuracy using surface operating parameters was poor as shown in Table 6. This may be due to impact of downhole condition such wellbore tortuosity and hole cleaning on the effective transfer of weight to the drill bit.

Fig. 8
figure 8

Plot of a cross-plot predicted versus actual data: b Error distribution curve c Complot with depth with [WOB, RPM

Full size image
Table 6 Sample of predicted versus actual ROP data using [WOB, RPM]
Full size table

Result of prediction using derived controllable variables (case 2)

The use of derived controllable variables to predict ROP was also performed keeping the same ANN configurations as in case 1. The modelling results delivered an excellent prediction with correlation coefficient (R2) of 0.985, RMSE of 7.6, and AAPE of 34. The model (a) the cross-plot of the actual versus predicted ROP, (b) error distribution curve, and (c) the comparison plot of actual versus predicted ROP with depth are shown in Fig. 9.

Fig. 9
figure 9

a Cross-plot predicted versus Actual ROP: b Error distribution c Complot with depth with [DMSE, FET]

Full size image

The numerical values comparison of the actual ROP and ANN predicted ROP using [DMSE, FET] is presented in Table 7. It can be observed that derived controllable variable predicted the ROP within acceptable level of accuracy across the heterogeneous lithologic columns, which implies that the performance of autonomous system can be better modelled using derived variables as a tuning parameter.

Table 7 Sample of predicted versus actual ROP data using [FET, DMSE]
Full size table

Discussion of result

The study used ANN modelling in the determination of appropriate tuning parameters for autonomous rotary drilling system in a complex heterogeneous formation by performing ROP prediction using proposed tuning variables. The adaptative self-optimizing capability of the system was investigated by evaluating the variation of the tuning parameters with changes in penetration rate across the heterogeneous rock. The following characteristics were maintained: (1) The ANN model was designed only for two input parameters each acting as a tuning parameter for the topdrive and the drawworks, respectively. (2) The predictive optimization model proposed two sets of tuning parameters: the actual surface operating parameter [WOB, RPM] and the derived energy parameters of [DMSE, FET] and tested their effectiveness as a controller variable with ROP predictions. (3) The actual surface parameter [WOB, RPM] could not accurately predict the drill rate in a complex heterogeneous formation because of the influence of downhole conditions such as wellbore tortuosity and torque and drag. Armentia (2008) identified these conditions for inefficient drilling. Therefore, ASP are not effective as an adaptive input parameter in autonomous system (4) The derived energy variable (DCV) performed excellently in effectively predicting the ROP with a high level of accuracy with a well-established trend with drill rate performance, thus proven to be an effective adaptive input parameter in autonomous system. 5) It was observed that the accuracy of the model depends on the quality and number of datapoints. The accuracy increases with increasing number of datapoint available. 6) The problem of overfitting in the model was avoiding by Splitting the datasets in 70:30 ratio for training and testing, respectively. Also, a new dataset was used in the validation of the model.

Sensitivity analysis

Sensitivity analysis was performed in the selection of optimum number of neutrons for the hidden layers. Results showed that the optimum number of 30 neutrons gave the highest accuracy which cannot be further improved. Figure 10 shows the results of the sensitivity analysis with number of neutrons at 1000 iterations performed using the derived controllable variable (DCV) at 10, 20, 30, and 40 neutrons, respectively.

Fig. 10
figure 10

Sensitivity analysis for the selection of optimal number of neutrons

Full size image

Model verification

Verification of the model was performed with dataset from a different wellbore (well-W1) which has total of 4185 datapoints. The performance result using the DCV and ASP is shown in Figs. 11 and 12, respectively. The prediction error of the DCV variable decreased with higher data density. Similarly, the performance of ASP was worst with higher data density with R2 value of 0.28 and RMSE of 25 and AAPE of 115, conversely the DCV variables, precisely predicted the actual measured ROP in a complex heterogeneous formation column with R2, RMSE, and AAPE values of 0.98, 3.4, and 34, respectively. The overall summary of result is presented in Table 5.

Fig. 11
figure 11

a Cross-plot predicted versus actual data: b Error distribution c Complot with depth with [DMSE, FET] for Well W1

Full size image
Fig. 12
figure 12

a Cross-plot predicted versus actual data: b Error distribution c Complot with depth with [WOB, RPM] for Well W1

Full size image

Conclusions

This research aimed at identifying appropriate tuning parameters and their predictive performance for self-optimizing autonomous rotary drilling systems using an artificial neural network with actual surface drilling parameters and derived controllable parameters. The following conclusions are reached based on the study;

  1. 1.

    The direct use of actual surface parameters (WOB, RPM) as tuning parameter for autonomous system produced a poor ROP prediction for drill rate with coefficient of determination (R2) of 0.74, RMSE of 28, and AAPE of 106 with well-P05 dataset, suggesting the inadequacy of using these two parameters alone.

  2. 2.

    The use of derived variables (DMSE, FET) as tuning parameter gave an excellent prediction accuracy with coefficient of determination (R2) of 0.98, RMSE of 7.6, and AAPE of 34 using same well-P05 dataset.

  3. 3.

    The result supports the decision to use the data-driven (ANN) model with derived controllable variables in the quantitative prediction of drilling rate for an autonomous drilling system.

  4. 4.

    Establishing a precise quantitative relation between derived variables and rate of penetration will improve parameter optimization, operational efficiency, and equipment reliability.

  5. 5.

    In achieving an optimized operating procedure, the auto-controller should monitor the resulting DMSE for the topdrive rotary speed an adjust parameter with the aim of achieving the lowest DMSE values.

  6. 6.

    Similarly, auto-controller will monitor the resulting feed thrust (FET) from the drawwork hoist and adjust parameter to attain a higher FET value provided all other drilling conditions such as hole cleaning and slick slip are within acceptable range.