Introduction

The fracture shape in real reservoirs varies; that is, the distribution, length, orientation, and capillary radius of a fracture network in nature are usually disordered, there are few methods to find its analytical solution, and it is difficult to accurately characterize it in a dual-porosity media seepage model (Yu et al. 2017; Liu et al. 2018a, b; Zheng and Yu 2012; Li et al. 2016; Wei and Xia 2017; Berkowitz et al. 2022). Therefore, a large number of researchers believe that fractal geometry is an effective method to describe dual-porosity media (Lei et al. 2019; Xu et al. 2016; Luo et al. 2021; Sun et al. 2015). In addition, whether it is an artificial pressure fracture or natural fracture, under the action of the original stress, the fracture surface will reveal a closed state or tendency (Ghanbarian 2021; Jiang et al. 2013; Zhu and Cheng 2018; Zhang et al. 2021). With the continuous reduction in the pressure of the oil and gas reservoir, the effective closure stress of the fracture surface will also increase. Therefore, it is particularly important to calculate the equivalent permeability of fractures under different stress states (Cai et al. 2017; Xia et al. 2021, 2019; Mandelbrot 2006; Sarkheil et al. 2012).

Meanwhile, the spontaneous imbibition model in porous media and the model of unidirectional flow and multiphase flow in porous media with capillary forces have been solved by researchers (Sanei et al. 2015; Rigby et al. 2004; Xu et al. 2012). Later, Yu et al. (2003) proposed a new method of fractal-Monte Carlo simulation and then used this method to study the permeability of porous media. However, the spherical seepage in porous media is also significant (Yu et al. 2003; Hassani et al. 2011; Sarkheil et al. 2013a, b); thus, the spherical flow in porous media is implied by employing fractal theory, and the fractal solution of two-phase flow considering capillary force is obtained by Miao et al. (2018).

Most unconventional reservoirs have dual-media seepage problems. Therefore, many scholars have used fractal theory to describe the fracture network and pore structure of the porosity matrix and constructed expressions for the equivalent permeability of dual media (Chen et al. 2012; Miao et al. 2018; Liu et al. 2018a, b; Sarkheil et al. 2013a, b; Sarkheil et al. 2009). Chiles and Marisly (1993) proposed the relationship between the linear density, surface density, and volume density of fractures. Berkowiz and Hada (1997) believe that both natural and synthetic fracture networks have fractal characteristics, in which fracture surface density and fractal dimension are closely related. Meng et al. (2011) found that the surface density of fractures is positively correlated with the fractal dimension of fractures, and the surface density and fractal dimension of fractures jointly determine the development degree of fractures. Jafari and Babadagli (2011) obtained the fractal permeability expression of random fractures by multiple regression analysis based on logging observation data, which contained many empirical constants.

However, these expressions did not include the microstructure parameters of fracture tortuosity. Miao et al. (2015) obtained only the fractal permeability expression, including the tortuosity of the porosity matrix, according to the basic fractal theory of dual-porosity media. Therefore, to describe the pore structure of dual-porosity media more accurately, the fractal dimension of the tortuosity of the capillary wall in the fracture network should be introduced.

Although there are many results on the influence of fracture parameters on permeability, there is a lack of research on the quantitative influence of the fracture tortuosity fractal dimension and fluid‒solid coupling coefficient on permeability. In this work, based on fractal geometry theory and models, a fractal model of equivalent permeability considering the tortuosity of fractures and the porosity matrix is established. The equivalent permeability of fractured porous media is calculated through the equation of fluid‒solid coupling between fractures and the porosity matrix. The accuracy of the proposed model is verified by comparing the flow rate obtained by the model prediction with the numerical simulation results, and a sensitivity analysis of each parameter in the model is carried out.

Theories and methodologies

In this section, we focus on the derivation of permeability models of the porosity matrix and fracture network, considering the fracture closure effect and fractal dimension of fracture tortuosity. The basis for calculating the equivalent permeability of dual-porosity media is presented in the next section.

Fractal theory for a porosity matrix

Many researchers have reported the fractal theory of porous media, which assumes that the matrix porous medium is composed of a bundle of curved capillaries, and the cumulative number of capillary diameters greater than or equal to r in the porous medium satisfies the following fractal scaling law (Yu et al. 2003):

$$N\left( {L \ge r} \right) = \left( {r_{\max } /r} \right)^{{D_{p} }}$$
(1)

The total number of pores in porous media is:

$$N_{{\text{t}}} \left( {L \ge r_{\min } } \right) = \left( {r_{\max } /r_{\min } } \right)^{{D_{p} }}$$
(2)

In general, the number of capillary tubes or pores in porous media is very large, so Eq. (1) can be regarded as a continuous and differentiable function. By differentiating both sides of Eq. (1), we can obtain:

$$- {\text{d}}N = D_{p} r_{\max }^{{D_{p} }} r^{{ - (D_{p} + 1)}} {\text{d}}r$$
(3)

The probability density function of the porosity size distribution can be obtained by dividing Eq. (3) by Eq. (2):

$$f(r) = D_{p} r_{\min }^{{D_{p} }} r^{{ - (D_{p} + 1)}}$$
(4)

The density function f(r) satisfies the normalization condition:

$$\int_{{r_{\min } }}^{{r_{\max } }} {f(r){\text{d}}r = 1 - \left( {r_{\min } /r_{\max } } \right)^{{D_{p} }} = 1}$$
(5)

If the above formula is true, the condition rmin/rmax <  < 1 is satisfied, and the fractal dimension and ratio (rmin/rmax) of the porosity of fractal porous media meet the following relation:

$$\phi_{m} = \left( {r_{\min } /r_{\max } } \right)^{{d_{{\text{E}}} - D_{p} }}$$
(6)

where dE is the Euclidean dimension, dE = 2 in 2D space, and dE = 3 in 3D space.

The tortuosity of a curved flow path in porous media is defined as τ = Lt/L0. The trace of fluid flow in a matrix curved capillary tub is usually curved and has fractal characteristics. The capillary diameter and length satisfy the following fractal scaling law:

$$L_{{\text{t}}} (r) = r^{{1 - D_{{\text{T}}} }} L_{0}^{{D_{{\text{T}}} }}$$
(7)

The total pore area representing the cross section of the unit is:

$$A_{{\text{p}}} = - \int_{{r_{\max } }}^{{r_{\min } }} {\frac{{\pi r^{2} }}{4}{\text{d}}N = } \frac{{\pi D_{p} r_{\max }^{2} (1 - \phi_{{\text{m}}} )}}{{4(2 - D_{P} )}}$$
(8)

The cross sectional area of the unit is:

$$A_{m} = \frac{{A_{{\text{p}}} }}{{\phi_{{\text{m}}} }} = \frac{{\pi D_{p} r_{\max }^{2} }}{{4\left( {2 - D_{p} } \right)}}\frac{{1 - \phi_{{\text{m}}} }}{{\phi_{{\text{m}}} }}$$
(9)

If the characterizing unit is assumed to be a cube and the length of the characterizing unit is \(L_{0} = \sqrt {A_{m} }\), according to Poiseuille’s law, the flow rate in a single curved capillary (Luo et al. 2021) is:

$$q(r) = \frac{\pi }{128\mu }\frac{\Delta p}{{L_{t} }}r^{4}$$
(10)

Substituting Eq. (7) into Eq. (10) and integrating between the minimum and maximum pore sizes of all capillary tubes on the whole element body, we can obtain:

$$Q_{{\text{m}}} = \frac{{\pi L_{0}^{{1 - D_{{\text{T}}} }} }}{128\mu }\frac{\Delta p}{{L_{0} }}\frac{{D_{p} }}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{T} + 3}} \left[ {1 - \left( {\frac{{r_{\min } }}{{r_{\max } }}} \right)^{{D_{{\text{T}}} - D_{p} + 3}} } \right]$$
(11)

Based on rmin <  < rmax, then

$$Q_{{\text{m}}} = \frac{{\pi L_{0}^{{1 - D_{T} }} }}{128\mu }\frac{\Delta p}{{L_{0} }}\frac{{D_{p} }}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 3}}$$
(12)

The permeability of the porosity matrix can be obtained from Darcy’s law:

$$K_{{\text{m}}} = \frac{{L_{0}^{{1 - D_{{\text{T}}} }} }}{32}\frac{{\phi_{m} }}{{\left( {1 - \phi_{m} } \right)}}\frac{{\left( {2 - D_{p} } \right)}}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 1}}$$
(13)

Fractal theory for a fracture network

Previous studies have shown that the fracture network can be analogized to countless capillary bundles that satisfy fractal scaling. According to basic fractal theory (Liu et al. 2018a, b), its fractal power-law relation is:

$$N( \ge r_{{\text{f}}} ) \propto r_{{\text{f}}}^{{ - D_{{\text{f}}} }} ,r_{{{\text{f}}\min }} \le r_{{\text{f}}} \le r_{{{\text{f}}\max }}$$
(14)

Due to the large number of fractures in the fracture network, by differentiating Eq. (14), the number of fractures in the fracture network with capillary radii between [r, r + dr] can be obtained as:

$$- {\text{d}}N(r_{{\text{f}}} ) = kD_{{\text{f}}} r_{{\text{f}}}^{{ - (D_{{\text{f}}} + 1)}} {\text{d}}r_{{\text{f}}} ,\, - {\text{d}}N(r_{{\text{f}}} ) > 0$$
(15)

The fracture probability density formula is:

$$- \frac{{{\text{d}}N(r_{{\text{f}}} )}}{{N_{{\text{t}}} }} = \frac{k}{N}D_{{\text{f}}} r_{{\text{f}}}^{{ - (D_{{\text{f}}} + 1)}} {\text{d}}r_{{\text{f}}} = f(r_{{\text{f}}} ){\text{d}}r_{{\text{f}}}$$
(16)

where Nt represents the total number of fractures, and the probability density of fractures is normalized as:

$$\frac{k}{{N_{{\text{t}}} }}\left( {r_{{{\text{f}}\min }}^{{ - D_{{\text{f}}} }} - r_{{{\text{f}}\max }}^{{ - D_{{\text{f}}} }} } \right) = \frac{k}{{N_{{\text{t}}} }}\frac{1}{{r_{{{\text{f}}\min }}^{{D_{{\text{f}}} }} }}\left( {1 - \left( {\frac{{r_{{{\text{f}}\min }} }}{{r_{{{\text{f}}\max }} }}} \right)^{{D_{{\text{f}}} }} } \right) = 1$$
(17)

When rfmin <  < rfmax, Eq. (17) can be expressed as:

$$k = N_{{\text{t}}} r_{{{\text{f}}\min }}^{{D_{{\text{f}}} }}$$
(18)

When rfmin/rfmax ≤ 10–2, natural fracture networks generally meet the following requirement.

$$f(r_{{\text{f}}} ) = D_{{\text{f}}} r_{{{\text{f}}\min }}^{{D_{{\text{f}}} }} r_{{\text{f}}}^{{ - (D_{{\text{f}}} + 1)}}$$
(19)

The total number of fractures in the fracture network is:

$$N_{{\text{t}}} (r_{{\text{f}}} ) = \left( {r_{{{\text{f}}\max }} /r_{{{\text{f}}\min }} } \right)^{{D_{{\text{f}}} }}$$
(20)

Substituting Eq. (20) into Eq. (18) yields the proportionality constant

$$k = r_{f\max }^{{D_{f} }}$$
(21)

Then, by substituting Eq. (21) into Eq. (15), the fractal power-law relation of the capillary radius of the fractal fracture can be obtained:

$$- {\text{d}}N(r_{{\text{f}}} ) = D_{{\text{f}}} r_{{{\text{fmax}}}}^{{D_{{\text{f}}} }} r_{{\text{f}}}^{{ - (D_{{\text{f}}} + 1)}} {\text{d}}r_{{\text{f}}}$$
(22)

Yu et al. (2003) proposed a fractal scaling relation for fluid flow through random and complex fracture networks

$$L_{{{\text{tf}}}} = r_{{\text{f}}}^{{1 - D_{x} }} L_{{\text{f}}}^{{D_{x} }}$$
(23)

The cross sectional area of all the capillaries in the fracture network (Luo et al. 2021) is:

$$\begin{aligned} A_{{\text{f}}} = & \int_{{r_{{{\text{f}}\min }} }}^{{r_{{{\text{f}}\max }} }} {\frac{{\pi r^{2} }}{4}{\text{d}}N\left( {r_{f} } \right)} \\ & = \frac{\pi }{4}\frac{{D_{{\text{f}}} }}{{2 - D_{{\text{f}}} }}\left[ {1 - \left( {\frac{{r_{{{\text{f}}\min }} }}{{r_{{{\text{f}}\max }} }}} \right)^{{1 - D_{{\text{f}}} }} } \right]r_{{{\text{f}}\max }} \\ \end{aligned}$$
(24)

Based on rmin <  < rmax, then

$$A_{{\text{f}}} = \frac{\pi }{4}\frac{{D_{{\text{f}}} }}{{2 - D_{{\text{f}}} }}r_{{{\text{f}}\max }}$$
(25)

To accurately describe the change in degree of fracture opening during the development process, it is assumed that the bulge of the fracture surface will not rupture during the effect of closure stress. In this case, the capillary diameter considering closure stress can be written as:

$$r_{f} = \left( {1 - \sigma_{eff} /E} \right)r_{fo}$$
(26)

The streamline length increases with increasing effective stress, as obtained by Gere and Goodno (2012):

$$L_{{\text{f}}} = \left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)L_{{{\text{fo}}}}$$
(27)

The relationship between the velocity and the pressure gradient of a single capillary tube in the fracture can be obtained by the Navier‒Stokes equation

$$q(r_{{\text{f}}} ) = \frac{\pi }{128\mu }\frac{{{\text{d}}p}}{{{\text{d}}L_{{{\text{tf}}}} }}r_{{\text{f}}}^{4}$$
(28)

If the total flow rate of the fluid through a component fracture collection is needed, the flow rate of the fluid through a single fracture should be obtained first, and then the minimum radius to the maximum radius of the capillary in all fractures on the entire characteristic element cross section should be calculated.

$$\begin{aligned} Q_{{\text{f}}} = & \int_{{r_{{{\text{f}}\min }} }}^{{r_{{{\text{f}}\max }} }} {q(r_{{\text{f}}} ){\text{d}}N(r_{{\text{f}}} } ) \\ & = \frac{{\pi \Delta pD_{{\text{f}}} r_{{{\text{fo}}\max }}^{{3 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{3 + D_{x} }} }}{{128L_{{{\text{fo}}}}^{{D_{x} }} \mu \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }}\left[ {1 - \left( {\frac{{r_{{{\text{f}}\min }} }}{{r_{{{\text{f}}\max }} }}} \right)^{{3 + D_{x} - D_{{\text{f}}} }} } \right] \\ \end{aligned}$$
(29)

In the two-dimensional plane, 0 < Df < 2, (rmin/rmax) 3+Dx−Df <  < 1, and according to Darcy’s law, the above equation can be simplified as:

$$K_{{\text{f}}} = \frac{{\pi D_{{\text{f}}} r_{fo\max }^{{3 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{3 + D_{x} }} }}{{128L_{{{\text{fo}}}}^{{D_{x} - 1}} A_{{\text{f}}} \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }}$$
(30)

Substituting Eq. (25) into Eq. (30), and if the fracture plane dip concerning the flow direction is θ, Eq. (30) can be written as:

$$K_{{\text{f}}} = \frac{{r_{{{\text{fo}}\max }}^{{2 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{2 + D_{x} }} \left( {2 - D_{{\text{f}}} } \right)\left( {\cos \theta } \right)^{{D_{x} - 1}} }}{{32L_{o}^{{D_{x} - 1}} \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }}$$
(31)

Equivalent permeability model of dual-porosity media based on fractal theory

According to the equivalent permeability of the porosity matrix and fracture network presented in the previous section, the flow rate expression of the porosity matrix and fracture network can be obtained as follows:

Porosity matrix:

$$Q_{{\text{m}}} = \frac{{\pi L_{0}^{{1 - D_{{\text{T}}} }} }}{128\mu }\frac{\Delta p}{{L_{0} }}\frac{{D_{p} }}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 3}}$$
(32)

Fracture network:

$$Q_{{\text{f}}} = \frac{{\pi \Delta pD_{{\text{f}}} r_{{{\text{fo}}\max }}^{{3 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{3 + D_{x} }} \left( {\cos \theta } \right)^{{D_{x} }} }}{{128L_{o}^{{D_{x} }} \mu \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }}$$
(33)

The characteristic units of the fracture network are larger than those of the pore matrix and contain multiple matrix units. Assuming Af = n Am, Eq. (9) and (26) can be obtained as follows:

$$\frac{\pi }{4}\frac{{D_{{\text{f}}} }}{{2 - D_{{\text{f}}} }}r_{{{\text{f}}\max }} = n \cdot \frac{{\pi D_{{\text{p}}} r_{\max }^{2} }}{{4(2 - D_{{\text{p}}} )}}\frac{{1 - \phi_{{\text{m}}} }}{{\phi_{{\text{m}}} }}$$
(34)

Ignoring the interaction between the fluid in the pores of the porosity matrix and the fluid in the fracture network, the inflow and outflow of the fracture are equal, so the total flow rate of the medium with dual-porosity can be expressed as:

$$\begin{aligned} Q =\, & Q_{t,m} + Q_{{\text{f}}} \\ & = n \cdot \frac{{\pi L_{0}^{{1 - D_{{\text{T}}} }} }}{128\mu }\frac{\Delta p}{{L_{0} }}\frac{{D_{p} }}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 3}} \\ & + \frac{{\pi \Delta pD_{{\text{f}}} r_{{{\text{fo}}\max }}^{{3 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{3 + D_{x} }} \left( {\cos \theta } \right)^{{D_{x} }} }}{{128L_{o}^{{D_{x} }} \mu \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }} \\ \end{aligned}$$
(35)

where

$$Q_{t,m} = n \cdot Q_{{\text{m}}}$$
(36)

The Newtonian fluid satisfies Darcy’s law; then, the permeability expression of Newtonian fluid with dual porous media is:

$$\begin{aligned} K =\, & n \cdot \frac{{L_{0}^{{1 - D_{{\text{T}}} }} }}{32}\frac{{\phi_{{\text{m}}} }}{{\left( {1 - \phi_{{\text{m}}} } \right)}}\frac{{\left( {2 - D_{p} } \right)}}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 1}} \\ & + \frac{{r_{{{\text{fo}}\max }}^{{2 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{2 + D_{x} }} \left( {2 - D_{{\text{f}}} } \right)\left( {\cos \theta } \right)^{{D_{x} - 1}} }}{{32L_{o}^{{D_{x} - 1}} \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }} \\ \end{aligned}$$
(37)

However, when the fluid‒solid coupling between the fracture network and porosity matrix is considered, the large error of the calculated permeability is compared with the actual permeability, resulting in an inaccurate reservoir description. Therefore, the permeability coupling factor is proposed to characterize the fluid‒solid coupling between the fracture network and porosity matrix, as shown in Eq. (38):

$$K_{t} = K_{{\text{m}}} + K_{{\text{f}}} \cdot (1 + k_{x} )$$
(38)

Then, the total permeability of the dual medium system is:

$$\begin{aligned} K_{t} =\, & \frac{{L_{0}^{{1 - D_{T} }} }}{32}\frac{{\phi_{{\text{m}}} }}{{\left( {1 - \phi_{{\text{m}}} } \right)}}\frac{{\left( {2 - D_{p} } \right)}}{{3 + D_{{\text{T}}} - D_{p} }}r_{\max }^{{D_{{\text{T}}} + 1}} \\ & + \frac{{r_{{{\text{fo}}\max }}^{{2 + D_{x} }} \left( {1 - \sigma_{{{\text{eff}}}} /E} \right)^{{2 + D_{x} }} \left( {2 - D_{f} } \right)\left( {\cos \theta } \right)^{{D_{x} - 1}} }}{{32L_{o}^{{D_{x} - 1}} \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma_{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }}\left( {1 + k_{x} } \right) \\ \end{aligned}$$
(39)

According to the lattice Boltzmann method, the equation of the permeability coupling factor is obtained by Yan (2019)

$$k_{x} = 0.123\phi_{{\text{m}}}^{0.838} H_{{\text{f}}}^{{ - 0.385\phi_{{\text{m}}}^{0.285} }}$$
(40)

Ultimately, the total permeability of the dual medium system is:

$$\begin{aligned} K_{t} = {\mkern 1mu} & \frac{{L_{0}^{{1 - D_{{\text{T}}} }} }}{{32}}\frac{{\phi _{{\text{m}}} }}{{\left( {1 - \phi _{{\text{m}}} } \right)}}\frac{{\left( {2 - D_{p} } \right)}}{{3 + D_{{\text{T}}} - D_{p} }}r_{{\max ^{{D_{{\text{T}}} + 1}} }} \\ & + \frac{{r_{{{\text{fo}}\max }}^{{2 + D_{x} }} \left( {1 - \sigma _{{{\text{eff}}}} /E} \right)^{{2 + D_{x} }} \left( {2 - D_{{\text{f}}} } \right)\left( {\cos \theta } \right)^{{D_{x} - 1}} }}{{32L_{o}^{{D_{x} - 1}} \left( {3 + D_{x} - D_{{\text{f}}} } \right)\left( {1 + \sigma _{{{\text{eff}}}} \upsilon /E} \right)^{{D_{x} }} }} \\ & \left( {1 + 0.123\phi _{{\text{m}}}^{{0.838}} H_{{\text{f}}}^{{ - 0.385\phi _{{\text{m}}}^{{0.285}} }} } \right) \\ \end{aligned}$$
(41)

Results and discussion

Taking the Yanchi Chang 8 area of the Ordos Basin as an example, the equivalent permeability of double porous media is calculated. In this section, we use the Darcy seepage equation to calculate the flow rate. To verify the accuracy of the model, the model in this paper and the numerical simulation model were calculated. The parameters of the fractal model are shown in Table 1.

Table 1 List of calculation parameters
Full size table

Figure 1 shows the predictions by the present model compared with those of the numerical simulation model and the fractal model. From Fig. 1, the fractal model predictions do not fit the numerical simulation results. In contrast, the present model predictions agree well with the numerical simulation data. Among them, the numerical simulation model is simulated by tNavigator, a commercial software developed by the Russian RFD company. Because the pore structure of rock satisfies the fractal geometry theory, the fractal model is Yu (Yu et al. 2003) numerical model proposed by A, which adopts the fractal distribution of pores. In this model, the porous medium is regarded as a space composed of fractal geometry.

Fig. 1
figure 1

Comparison of flow rate under different total permeability models

Full size image

By deriving the permeability equation of fractured reservoirs considering fracture closure, a series of flow rate charts were calculated and plotted to conduct sensitivity analysis. Below, the influence of fracture network parameters on flow rate is presented first, and then the effects of some key parameters on flow rate, including the fractal dimension of fracture tortuosity, maximum radius of the fracture network, and the physical parameters of the fracture network, are further discussed. For this case, consider fracture closure by Young’s modulus (E), Poisson’s ratio (ν), and effective stress (σeff) on a fracture network. Second, influence of the porosity matrix parameters on the flow rate is discussed, including the fractal dimension of the porosity matrix, fractal dimension of the porosity matrix tortuosity, maximum capillary radius, and matrix porosity.

Influence of fracture parameters on the flow rate of the permeability model

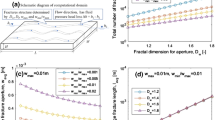
Figure 2 displays the effect of the fractal dimension of the fracture network and fracture tortuosity on the flow rate. The fractal dimension of the fracture and fracture tortuosity is negatively correlated with the flow rate. For a fixed fractal dimension of fracture tortuosity, a decrease in flow rate can be observed as the fractal dimension of the fracture increases. Meanwhile, the fractal dimension of fracture tortuosity has a larger impact on flow rate than the fractal dimension of fracture, and then the decreased range of flow rate decreases with the increase in the fractal dimension of fracture tortuosity and fracture. When the fractal dimension of the fracture tortuosity increased from 1.0 to 1.5, the flow rate decreased by 68.7%; when the fractal dimension of the fracture increased from 1.0 to 1.5, the flow rate decreased by 43.7%.

Fig. 2
figure 2

Effect of the fractal dimension of the fracture network and fracture tortuosity on the flow rate

Full size image

For a fixed fractal dimension of fracture, Fig. 3 shows the effect of the maximum fracture radius on the flow rate. It can be seen in Fig. 3 that the fracture radius has a significant effect on the flow rate. The fracture radius is positively correlated with the flow rate, and an increase in flow rate can be seen as the fracture radius increases.

Fig. 3
figure 3

Effect of the fractal dimension of fracture surface tortuosity and maximum fracture radius on the flow rate

Full size image

Subsurface porous media rocks are composed of rock particles and pore fluids. During the development stage of the reservoir, compression of the rock will generate compound stress, which will lead to the deformation and displacement of the rock skeleton (Fig. 4). When the pore fluid migrates with the rock skeleton, relative seepage will also occur (Cao 2016; Wang et al. 2019).

Fig. 4
figure 4

Schematic diagram of forces acting on a rock element (Dai., 2006). Notes: σx, σy, σz are normal stresses in the x, y, and z directions; τxy and τyx are shear stresses on the x and y planes; τxz and τzx are shear stresses on the x and z planes; τyz and τzy are shear stresses on the y and z planes

Full size image

As shown in Fig. 4, the reservoir rock can be equivalently regarded as a single hexahedral unit (Dai 2006; Feng et al. 2018). The opposite sides of the regular hexahedral elements are parallel to each other. Along the x, y, and z axes, the lengths of each side of the hexahedral unit correspond to dx, dy, and dz, respectively. The nine components on the reservoir rock are shown in Eq. (42). Moreover, the size of the nine components is related not only to the direction of the coordinate axis but also to the force of the point. The stress state at a certain point inside the rock can be represented in the form of a matrix:

$$\sigma_{ij} = \left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ {\tau_{yz} } & {\sigma_{y} } & {\tau_{yx} } \\ {\tau_{zx} } & {\tau_{zy} } & {\sigma_{z} } \\ \end{array} } \right]$$
(42)

Chen and Ewing (Chen and Ewing 1999) used the elastic physical equation of porous media to describe the relationship between the effective stress and strain of rock, and its general expression is:

$$\left\{ {\sigma_{{{\text{eff}}}} } \right\} = f\left( {\left\{ \varepsilon \right\}} \right)$$
(43)

where {σeff} is the stress vector of the rock skeleton, m; and {ε} is the strain vector of the rock skeleton, m.

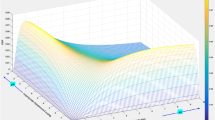
Meanwhile, as displayed in Fig. 5, Young’s modulus has a significant influence on the flow rate. The flow rate increases significantly under the same Poisson’s ratio, and when Young’s modulus is between 1 and 10 GPa, the range of the flow rate change is relatively obvious. As shown in Fig. 5, the effect of Poisson’s ratio on the flow rate is negligible.

Fig. 5
figure 5

Effect of Young’s modulus (E) and Poisson's ratio (ν) of a fracture network on the flow rate

Full size image

Similarly, Fig. 6 shows that the flow rate gradually increases with increasing fracture inclination angle and slowly decreases in the initial stage, but with increasing fracture inclination angle in the later stage, the flow rate reduction rate is accelerated. According to the result analysis presented in Fig. 6, in this model, when the fractal dimension of the fracture network is 1, there is no correlation between the fracture inclination angle and flow rate.

Fig. 6
figure 6

Effect of the fractal dimension of the fracture surface tortuosity and inclination of the fracture direction relative to the horizontal direction

Full size image

Influence of porosity matrix parameters on the flow rate of the permeability model

Figure 7 displays the effect of the fractal dimension of the porosity matrix and porosity matrix tortuosity on the flow rate. The fractal dimension of the porosity matrix and porosity matrix tortuosity are negatively correlated with the flow rate. For a fixed fractal dimension of porosity matrix tortuosity, a decrease in flow rate can be observed as the fractal dimension of the porosity matrix increases. Meanwhile, the decreased range of the flow rate decreases with the increase in the fractal dimension of the porosity matrix tortuosity and porosity matrix. When the fractal dimension of the porosity matrix tortuosity increased from 1.0 to 1.5, the flow rate decreased by 0.9%; when the fractal dimension of the porosity matrix increased from 1.0 to 1.5, the flow rate decreased by 0.8%.

Fig. 7
figure 7

Effect of the fractal dimension of the porosity matrix and porosity matrix tortuosity on the flow rate

Full size image

As shown in Figs. 8 and 9, the maximum porosity matrix radius and matrix porosity are positively correlated with the flow rate, but these two parameters have little impact on the flow rate.

Fig. 8
figure 8

Effect of the fractal dimension of porosity matrix surface tortuosity and the maximum capillary radius of rock matrix on the flow rate

Full size image
Fig. 9
figure 9

Effect of the fractal dimension of the porosity matrix tortuosity and porosity matrix porosity on the flow rate

Full size image

Through comparison, we found that the fracture parameters have a significant influence on the porosity matrix parameters and the flow rate. In particular, the maximum fracture radius, the fractal dimension of the fracture network, and fracture tortuosity have a significant influence on the flow rate, while the effect of the fractal dimension of the porosity matrix and porosity matrix tortuosity on the flow rate is weak. The difference between the fracture network and porosity matrix may demonstrate that the permeability of the fracture network is dominant in the equivalent permeability of dual-porosity media.

Conclusions

  1. (1)

    The equivalent permeability of dual-porosity media can be described more accurately by considering the effect of stress closure and the fluid‒solid coupling coefficient.

  2. (2)

    The fractal dimension of the fracture diameter and tortuosity has a great effect on the equivalent permeability, and the fractal dimension of the fracture diameter and tortuosity is negatively correlated with the flow rate and equivalent permeability.

  3. (3)

    The fracture closure effect has a weak influence on the flow rate, while the maximum fracture radius has a significant effect on the flow rate. With the increase in the fractal dimension of the fracture surface tortuosity, the rising trend of the flow rate slows with the increase in the maximum fracture radius.

  4. (4)

    When the fracture inclination is less than 45°, it has a weak impact on the dual-porosity medium equivalent permeability; when the fracture inclination is greater than 45°, it has a significant impact on the dual-porosity medium equivalent permeability.

  5. (5)

    With the increase in the fracture inclination angle, there is a significant decrease in the flow rate under the same fracture dimension of fracture surface tortuosity. When the fractal dimension of the fracture network is 1, there is no correlation between the fracture inclination angle and flow rate.

  6. (6)

    The maximum matrix porosity radius and the matrix porosity are both positively correlated with the flow rate and equivalent permeability. The fractal dimensions of the matrix surface tortuosity and porosity matrix are both negatively correlated with the flow rate and equivalent permeability.