A comprehensive method for determining the dewaxing interval period in gas lift wells

Abstract

The gas lift method is an artificial lift method of well production using the energy of compressed gas injected into the well to lift the reservoir fluid to the surface. The formation of paraffin deposits has remained one of the critical oil production problems due to the growing percentage of hard-to-recover reserves in the overall structure. This complication is also typical for many oil and gas fields in Vietnam, such as the White Tiger, White Bear, and Dragon fields. Wax deposit formation negatively affects the operation of individual production wells and the development of the field as a whole, which leads to a decrease in productivity and the need to take measures to remove paraffin deposits, subsequently increasing the downtime period of the well. In order to ensure stable production of highly paraffinic oil, it is necessary to take measures to dewax wells systematically. The frequency of wax removal operations depends on the intensity of the wax formation, which is determined by various technological, technical, and geological factors. The interval between dewaxing operations is called the dewaxing interval period (DIP). This value is an important technological parameter and characterizes the efficiency of a well’s operation. In this study, a comprehensive method has been developed to determine the dewaxing interval period (treatment interval) for gas-lift wells when the formation of wax deposits has occurred. The optimal dewaxing interval period is suggested to be determined by the change in the liquid well flow rate at the point when it falls by 20% from the initial value. In addition, a mathematical model of the time-dependent wax thickness, taking into account the heat and mass transfer laws and the laboratory results using the Cold Finger method, has also been developed. The proposed model for determining the dewaxing interval period was applied to an oil well in Vietnam. The DIP prediction model gave a similar value to the actual DIP field data (6.67 and 6 days, respectively). The obtained results showed that the model had proven its accuracy following the results of a comparison with the field's data of dewaxing operations.

Introduction

The gas lift method of well operation is an artificial lift method of production using the energy of compressed gas injected into the well to lift the reservoir fluid to the surface (Feder 2019;  Burkhanov et al. 2022).

An essential feature of the gas lift method is a wide range of possible gas injections, which allows it to be used for the operation of wells with both low (less than 40 m³/day) and high flow rates (up to 1600 m³/day), as well as for oil wells with high gas factors and with bottom-hole pressures below the bubble point (Aleksandrov et al. 2019; Li et al. 2019; Van et al. 2022; Dvoynikov 2018).

Continuous and periodic gas lift methods of well operation are chosen, depending on the specific conditions of the formation, as well as the geological and technical characteristics of a well. For the continuous gas lift, the gas is continuously injected at a predetermined depth into the lifting column. However, for periodic gas lift, gas is injected periodically, as a particular volume of liquid accumulates in the tubing above the planned gas inlet point (Proshutinskiy et al. 2022; Kasumu and Mehrotra 2013; Neto et al. 2010; Rogachev et al. 2021). In this paper, the continuous gas lift was considered.

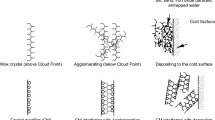
Paraffin deposition usually occurs during waxy oil production and in low-temperature production areas. The wax appearance temperature (or cloud point) is the temperature at which paraffin begins to crystallize in a liquid. As the temperature continues to drop, the precipitated wax particles interact and form a spatially linked network. At a certain temperature, waxy oil will solidify and stop flowing. This temperature is called the pour point of crude oil (Ilyushin et al. 2019; Ito et al. 2021; Zhao et al. 2017; Ulyasheva et al. 2020).

Temperature drop might occur on the wall of the tubing or the oil transportation system as a result of gas expansion or heat loss through the casings, ring spaces, and areas around the well, as well as the environment around the pipeline systems, such as land, water, and air (Tananykhin et al. 2022; Lira‐Galeana et al. 1996). Paraffin crystals are precipitated from the crude oil during the accumulation process as separate molecules, and these crystals exist in the liquid as a dispersed phase (Bimuratkyzy et al. 2016; Neto et al. 2010). They tend to form solids around the crystalline nuclei of asphaltene with mechanical impurities to develop into relatively large particles. Paraffin deposition is usually a result of the following mechanisms: molecular diffusion, sliding dispersion, Brownian motion, gravity effects, and electrodynamic effects (Beloglazov et al. 2021; Adebola S Kasumu et al. 2013; Sevic et al. 2017; Sultanbekov et al. 2021).

The presence of paraffin contributes to the following issues: a reduction in the diameter of the production tubing and the surface of the transportation pipeline, a reduction in the permeability coefficient, a requirement of a considerable amount of pressure to restart the flow, a significant reduction in the flow pressure in the pipeline, and a limit to the operating capacity of the entire production system. The mentioned factors lead to a range of problems, such as a decrease in production and a limit to the transportation of crude oil by pipelines. As a result, the wax deposition might cause blockages and corrosion of the pipeline, increasing the operational expenses due to the temporary delay of the production and transportation systems from processing high-wax oils (Bian et al. 2019; Creek et al. 1999; Adebola S Kasumu et al. 2013; Zheng et al. 2017; Zougari et al. 2006).

The formation of paraffin deposits has remained one of the critical oil production problems due to the growing percentage of hard-to-recover reserves in the overall structure. This complication is also typical for many oil and gas fields in Vietnam (White Tiger, White Bear, Dragon fields, etc.). Wax deposit formation negatively affects the operation of an individual production well and the development of the field as a whole, which leads to a decrease in productivity and the need to take measures to remove paraffin deposits, subsequently increasing the downtime period of the well (Akhmadeev et al. 2016; Akhmadeev et al. 2019a, b; Akhmadeev et al. 2017; Aleksandrov et al. 2019; Nguyen et al. 2021; Rogachev et al. 2021; Van et al. 2022).

In order to solve the problem of paraffin wax formation, studies have been carried out, focusing on two main directions: preventing/limiting the wax deposition during production and transportation of high-wax oil, and removing paraffin deposits. Nevertheless, the question of finding the ultimate method to eradicate wax deposition has remained unsolved (Creek et al. 1999; Kasumu et al. 2013; Theyab et al. 2018; Nikolaev et al. 2019; Khaibullina 2020).

Paraffin deposition still occurs after applying prevention methods. Therefore, many methods have been combined to achieve the highest prevention and treatment efficiency in handling paraffin deposition problems. Vietnamese oil and gas companies mainly apply traditional paraffin deposition methods during production, such as mechanical methods, hot-oil circulation, and superheated steam treatment. In addition, in some production wells, a pour point depressant (PPD) metering pump system is installed into the production oil stream at a depth of about 2000–2500 m to remediate the formation of paraffin deposition in the tubing (Akhmadeev et al. 2016; Podoprigora et al. 2017; Raupov et al. 2022).

In order to ensure stable production of highly paraffinic oil, it is necessary to take measures to dewax wells systematically. The frequency of wax removal operations depends on the intensity of wax formation, which is determined by various technological, technical, and geological factors (Craddock et al. 2007; Rogachev et al. 2021; Smyshlyaeva et al. 2021; Thota and Onyeanuna 2016; Sousa et al. 2019).

The interval between dewaxing operations is called the dewaxing interval period (DIP). This value is an important technical parameter and characterizes the efficiency of its operation.

In recent decades, oil companies have adhered to a reactive strategy, according to which wells have been dewaxed in the event of a considerable amount of deposit in the tubing. Wax detection in a well can be carried out by various direct and indirect methods (Azevedo et al. 2003; Fadairo et al. 2010; Japper-Jaafar et al. 2016; Phillips et al. 2011; Swivedi et al. 2013). The advantage of the latter is the applicability without the downtime of a well by monitoring the parameters of its operation. The operation parameters change as the thickness of the deposits increases. Nonetheless, for the most part, detecting wax deposits requires the formation of deposits of considerable thickness. Thus, this approach to detecting complications results in a significant delay, which increases the negative impact on the production process and can lead to significant consequences. Accordingly, the use of methods for predicting the optimal DIP based on mathematical models describing the process of wax formation appears to be more relevant.

Based on heat transfer and mass transfer laws, the existing models have suggested that molecular diffusion is the key mechanism of wax formation (Decker et al. 2018; Mardashov 2021; Li et al. 2019). This study investigates the intensity of wax deposition using a cold finger device. According to the literature reviews, many researchers have also studied the kinetics of wax deposition employing the cold finger (Eskin et al. 2013; Hu et al. 2019; Ito et al. 2021; Li et al. 2019; Lira‐Galeana et al. 1996; Phillips et al. 2011). The authors stated that four zones were formed in their models. The authors also proposed that heat and mass transfer co-occurred in the boundary layer, and the temperature profile strongly influenced the wax concentration profile. As the temperature drops below the wax appearance temperature, wax precipitates in the thermal boundary layer. Hence, the concentration of the dissolved wax in the layer is subject to the temperature profile. In addition, the kinetics of wax precipitation is rapid and much faster than the wax molecule diffusion rate (Hu et al. 2019; Podoprigora et al. 2022; Tananykhin et al. 2021).

A significant portion of the scientific papers has focused on developing mathematical models to study the intensity of wax formation (Gizatullin 2020; Feder 2019; Haj-Shafiei et al. 2014; Swivedi et al. 2013; Theyab et al. 2018; Mardashov et al. 2022). Nevertheless, these models are used exclusively to estimate the thickness of the formed deposits and do not carry significant practical value. Therefore, an improvement of a mathematical model describing the time dependence of the wax thickness would be of paramount importance to developing the optimal dewaxing interval period, which would broaden the application of the aforementioned studied. As a result, introducing these models into the production process is potentially conducive to increasing the effectiveness of a set of operations to combat the wax formation in oil and gas fields.

The novelty of this paper is to develop a method for determining the dewaxing interval period (treatment interval) for gas-lift wells in conditions complicated by wax deposit formation, based on the laws of heat and mass transfer and the results of experiments using the Cold Finger method. The developed model for determining the dewaxing interval period was applied to a gas lift oil well in Vietnam. The obtained results show that the model had proven its accuracy according to a comparison with the field's data of dewaxing operations.

Materials and methods

The high-wax oil model used in this study was the degassed oil from the basement formation in the Dragon field in Vietnam. The oil was characterized by high-wax content (24.03%) with a melting point of 32.5 °C, and the wax appearance temperature was 58 °C (Akhmadeev et al. 2019a, b; Nguyen et al. 2021; Van et al. 2022). The intensity of wax formation was studied using the "cold finger" device, the manufacturer of which is F5 Technologies (Fig. 1).

Fig. 1

The intensity of wax deposit formation

Dynamic coaxial cells simulate flow conditions in the tubing by applying a slide to a cold finger surface where the deposition occurs. The deposited layer accumulating on the surface of the cold finger is similar to waxy, paraffin, resin, colloid, asphaltene, and liquid oil.

The coaxial cell contains a stainless-steel cylinder, which is cooled from the inside by a circulating liquid from a water bath. There is an outer heating layer on the oil bottle to maintain the temperature of the oil. The slide effect is produced on the cold finger’s surface by rotating the outer cylinder at a controlled speed to simulate the sliding velocity delivered by the fluid flow in the actual pipeline.

The experiment's methodology consisted of preliminary obtaining anhydrous waxy oil from basement formation in the Dragon field. Further, in the required amount, the studied samples were poured into sealed cells of a six-place installation and kept for 30 min in a thermostat (water bath) installed on a magnetic stirrer at a temperature of 60 °C.

The mass was determined by removing deposits from the surface of the finger with a scraper and then weighing them.

When studying the kinetics of the wax formation, the mass of deposits (m) was considered time-dependent. 250 ml of waxy oil was collected in a laboratory/chemical beaker. The oil and cold finger temperatures were 60 °C and 30 °C, respectively. At a constant temperature (T = 60 °C) and the stirring frequency (300 rpm), the deposit's mass measurements were taken at 3, 5, 10, 15, 20, 25, 30, and 60 min. After a period of deposition, the cold finger was removed from the oil. It was then placed in an oven at 30 °C to dry and prevent significant sticking of the gelled oil. After drainage, paraffin residues were removed and weighed. The mass was determined by removing deposits from the surface of the finger with a scraper and then weighing them. The experiment was carried out twice.

Evaluation of the dewaxing interval period

The gas lift method of well operation is an artificial lift method of production using the energy of compressed gas injected into the well to lift the reservoir fluid to the surface.

An essential feature of the gas lift method is a wide range of possible gas injections, which allows it to be used for wells' operation with both a low (less than 40 m³/day) and a high flow rate (up to 1600 m³/day), along with wells with high gas factors and bottom-hole pressures below the bubble point.

Continuous and periodic gas lift methods of well operation have been chosen, depending on the specific conditions of the formation and geological technical characteristics of a well. For the continuous gas lift, the gas is continuously injected at a predetermined depth into the lifting column. However, for periodic gas lift, gas is injected periodically, as a particular volume of liquid accumulates in the lifting pipes above the planned gas inlet point. In this paper, the continuous gas lift was studied.

Choosing equipment and operating mode of wells during gas-lift operation is subject to different principles. When calculating a gas lift, the primary condition is a minimum of the specific gas consumption or energy spent on its compression.

The operating condition of the gas-lift well is shown as following (1) (Feder 2019):

$$G(1 - \sigma _{f} )\left[ {1 - \frac{{P_{c} + P_{w} }}{{P_{s} }}} \right](1 - B) + R \ge \frac{{0.388 \cdot L_{c} (\rho _{L} gL_{c} - P_{c} + P_{w} )}}{{d^{{0,5}} (P_{c} - P_{w} )\log \frac{{P_{c} }}{{P_{w} }}}},$$

(1)

where

$G$: gas oil ratio, m³/ m³;

$\sigma_{f}$: natural separation of the free gas near the hoist’s shoe coefficient, unit fraction;

$P_{c}$: bottom-hole pressure, MPa;

$P_{{\text{w}}}$: wellhead pressure, MPa;

$P_{s}$ – saturation pressure (bubble point pressure), MPa;

$B$ – well stream water-cut, unit fraction;

$L_{c}$ – well depth, m;

$\rho_{L}$ – well fluid density, kg/m³;

$d$ – production tubing diameter, m;

$R$ – specific gas flow rate, m³/ m³, which is calculated by following (2):

$$R = \frac{{Q_{g} }}{{Q_{o} }},$$

(2)

where

$Q_{g}$ – gas flow rate, m³/d;

$Q_{o}$ – oil flow rate, m³/d.

The equality corresponds with the minimum indispensable pressure for gas-lift oil production. The left side of Eq. (1) is the effectively acting gas factor $G_{e}$, m³/ m³. The right side of Eq. (1) is the optimal specific gas flow rate in the hoist while gas-lift operating $R_{o}$, m³/ m³.

Separation coefficient $\sigma_{f}$ is determined through formula (3):

$$\sigma_{f} = \frac{{\sigma_{0} }}{{1 + 0.7\frac{{q_{L} }}{{v_{0} F_{k} }}}},$$

(3)

where

$q_{L}$ – volumetric fluid flow rate near the string shoe, m³/s;

$v_{0}$ – relative speed of the gas phase near the string shoe, m/s;

$F_{k}$ – Cross sectional area of the casing column, m²;

$\sigma_{0}$ – free gas’ natural separation coefficient of the zero injection, according to (4):

$$\sigma_{0} = 1 - \left( {\frac{{d_{e} }}{D }} \right)^{2} ,$$

(4)

where

$d_{e}$ – external diameter of the production tubing, m;

$D$ – inner diameter of the casing string, m.

Relative speed of the gas phase near the string shoe is determined by following expressions (5):

$$\left. {\begin{array}{*{20}l} {if} \hfill & {B < 0.4} \hfill & {v_{0} = 0.023\;m/s,} \hfill \\ {if} \hfill & {0.4 < B < 0.5} \hfill & {v_{0} = 0.023 + 0.82(B - 0.4),} \hfill \\ {if} \hfill & {B > 0.5} \hfill & {v_{0} = 0.105 + 0.23(B - 0,5)} \hfill \\ \end{array} } \right\}$$

(5)

The equation of inflow (6):

$$Q_{L} = K_{pi} (P_{f} - P_{c} ),$$

(6)

where

$Q_{L}$ – fluid flow rate of the gas-lift well, m³/d;

$_{pi}$ – productivity index, m³/d/MPa;

$P_{f}$ – formation pressure, MPa.

Putting (2), (6) into (1), the result is (7):

$$\begin{aligned} & G(1 - \sigma _{f} )\left[ {1 - \frac{{P_{c} + P_{w} }}{{P_{s} }}} \right](1 - B) + \frac{{Q_{g} }}{{K_{{pi}} (P_{f} - P_{c} )}} \\ & \quad \ge \frac{{0.388 \cdot L_{c} (\rho _{L} gL_{c} - P_{c} + P_{w} )}}{{d^{{0,5}} (P_{c} - P_{{\text{w}}} )\log \frac{{P_{c} }}{{P_{{\text{w}}} }}}}, \\ \end{aligned}$$

(7)

The solution $P_{c}$ of Eq. (7) is the intersection point of the effective gas factor $G_{e}$ curve and optimal specific gas flow rate curve $R_{o}$ in the tubing during gas-lift $R_{o}$(Fig. 2).

Fig. 2

The influence of the alteration of the diameter of the production tubing to the minimum bottom-hole pressure

During the gas lift exploitation in the environment of the solid paraffin formation, the diameter of the production tubing decreases. With the decline of the production tubing diameter, the optimal specific injected gas flow rate $R_{o}$ increases. As a result, the bottom-hole pressure $P_{c}$ grows. According to (6), with a rise of the bottom-hole pressure $P_{c}$, production rate gas-lift well falls throughout the period. The dewaxing interval period is determined by the change in the liquid well flow rate $Q_{L}$, at the point when it falls by 20% from the initial value. Well parameters are presented in Table 1.

Table 1 Parameters of the gas-lift well in the Dragon field

Therefore, $\sigma_{0} = 1 - \left( {\frac{{d_{e} }}{D }} \right)^{2} = 1 - \left( {\frac{0.073}{{0.172}}} \right)^{2} = 0.82$.

Separation coefficient: $\sigma_{f} = \frac{{\sigma_{0} }}{{1 + 0.7\frac{{q_{L} }}{{v_{0} F_{k} }}}} = \frac{0,82}{{1 + 0.7\frac{{\frac{1.548}{{0.1013 \cdot 86400}}}}{{0.023 \cdot \pi \frac{{0.172^{2} }}{4}}}}} = 0.666$.

The oil’s average density was determined by the formula:

$$\rho_{o} = (\rho_{d} + \rho_{f} )/2 = (843 + 709)/2 = 776\,\,({\text{kg}}/{\text{m}}^{{3}} )$$

When substituting the initial and calculated values of the well parameters into Eq. (1), we get following result (8):

$$G(1 - \sigma_{f} )\left[ {1 - \frac{{P_{c} + P_{w} }}{{P_{s} }}} \right](1 - B) + \frac{{Q_{g} }}{{K_{pi} (P_{f} - P_{c} )}} = \frac{{0.388 \cdot L_{c} (\rho_{L} gL_{c} - P_{c} + P_{w} )}}{{d^{0,5} (P_{c} - P_{{\text{w}}} )\log \frac{{P_{c} }}{{P_{{\text{w}}} }}}}$$

$$\Leftrightarrow 44.897\left( {\frac{{12.7 - P_{c} }}{13.7}} \right) + \frac{1308.786}{{19.4 - P_{c} }} = \frac{{1564.8 \cdot (31.7 - P_{c} )}}{{d^{0,5} (P_{c} - 1)\log P_{c} }},$$

(8)

If $t = 0;d = d_{0} = 57.3mm$, there is no solid paraffin formation, therefore:

$$\Leftrightarrow 44.897\left( {\frac{{12.7 - P_{c} }}{13.7}} \right) + \frac{1308.786}{{19.4 - P_{c} }} = \frac{{1564.8 \cdot (31.7 - P_{c} )}}{{57.3^{0,5} (P_{c} - 1)\log P_{c} }}$$

$\Leftrightarrow 3.278\left( {12.7 - P_{c} } \right) + \frac{1308.786}{{19.4 - P_{c} }} = \frac{{206.72 \cdot (31.7 - P_{c} )}}{{(P_{c} - 1)\log P_{c} }}.$.

Figure 3 shows the bottom hole pressure obtained at d = d₀, corresponding to the value at the intersection point.

Fig. 3

Determining the value of bottom-hole pressure at $d_{0} = 57.3$ mm (without paraffin)

For the most part, the dewaxing interval period is determined by the change in the bottom-hole pressure, which depends on the changes in the diameter of production tubing. In addition, during high-waxy oil production, the tubing diameter is highly subject to the intensive formation of paraffin deposits. Therefore, to determine the DIP, it is of utmost importance to determine the time dependence of the wax thickness. However, according to the literature reviews, there is no relevant report studying the time dependence of the wax thickness. In this paper, the authors developed a mathematical model of the time-dependent wax thickness, taking into account the heat and mass transfer laws and the laboratory results. Subsequently, the model has been used to determine the dewaxing interval period of a gas lift well.

Determination of the thickness of the paraffin formation by heat transfer

The change in the thickness of paraffin deposits over time is determined by the following mathematical model.

Determining oil’s heat transfer coefficient

When determining the heat transfer coefficient of the oil, the thermal similarity parameter, the Nusselt (Nusselt) criteria were used, which is determined by formula (9):

$${\rm Nu} = 0.021 \cdot \text{Re} _{{f,d}}^{{0.8}} \cdot \mathop {\Pr }\limits_{f}^{{0.43}} \cdot \overline{{\varepsilon _{\ell } }} ,$$

(9)

where

Re – Reynolds number, dimensionless;

Pr – Prandtl criteria, dimensionless;

$\overline{{\varepsilon_{\ell } }}$ – is the correction, taking into account the change in the heat transfer coefficient in the initial part of hydrodynamic and thermal stabilization:

– at ${\ell \mathord{\left/ {\vphantom {\ell d}} \right. \kern-0pt} d}$ > 50 $\overline{{\varepsilon_{\ell } }}$ = 1;

– at ${\ell \mathord{\left/ {\vphantom {\ell d}} \right. \kern-0pt} d}$ < 50 $\overline{\varepsilon }_{\ell } \approx 1 + 2{d \mathord{\left/ {\vphantom {d \ell }} \right. \kern-0pt} \ell }$.

In this case $\overline{{\varepsilon_{\ell } }}$ = 1.

Heat transfer coefficient of the individual liquid hydrocarbons is calculated by formulas (10–11):

$$\lambda_{o} = 0.1717 - 0.385 \cdot 10^{ - 3} \cdot M_{o} ,$$

(10)

$$Nu = \frac{\alpha \cdot d}{\lambda },$$

(11)

where

$\lambda_{o}$– thermal conductivity of oil, W/(m‧°C).

M_o – molar mass of the oil, g/mol;

$\alpha$– heat transfer coefficient of the oil, ${\rm W/m^{2} \cdot K}$.

Reynolds number, according to (12):

$${\text{Re}} = \frac{{4Q_{L} \rho_{L} }}{{\pi \mu d_{h} }},$$

(12)

where

$d_{h}$ – hydraulic diameter of the tube, м;

$\rho_{L}$ – well fluid density, kg/m³;

$Q_{L}$ – liquid flow rate of a gas-lift well ${\rm m^{3} /d}$.

The Prandtl criteria are determined by the formula: $\Pr = \frac{{\mu_{L} \cdot_{p} }}{{\lambda_{L} }}$.where

$C_{p}$–heat capacity at a constant pressure, J/(kg‧°C).

Therefore, the heat transfer coefficient is determined by the ratio (13):

$$\alpha = 0.021 \cdot {\text{Re}}_{f,d}^{0.8} \cdot \Pr_{f}^{0.43} \cdot \overline{{\varepsilon_{\ell } }} \cdot \frac{{\lambda_{o} }}{d},$$

(13)

For laminar flow (14):

$$\alpha = 4\frac{{\lambda_{o} }}{d},$$

(14)

A model of the heat transfer

Figure 4 shows the layout of the main zones with different heat transfer parameters for the principal system of a "Cold Finger".

Fig. 4

Cold Finger system geometry

To study the wax formation using the proposed model, the heat transfer process is considered in three zones (Fig. 4) and the system is considered to be adiabatic on the outer wall of the cylinder (Creek et al. 1999; Hu et al. 2019; Ito et al. 2021; Phillips et al. 2011):

• 1. Paraffin layer – $\Delta T$ between $T_{f}$ and $T_{p}$ ;

• 2. Boundary layer – $\Delta T$ between $T_{p}$ and $T_{bl}$ ;

• 3. Oil flow – $\Delta T$ between $T_{bl}$ and $T_{os}$ .

According to the theory of molecular diffusion, radial diffusion of the particles occurs only in the volume of the boundary layer, in the interval [$R_{p}$; $R_{cf}$]. Therefore, in the absence of a layer of deposited paraffin ($R_{f} = R_{p}$, $t = 0,T_{p} = T_{f}$) the effect of mass diffusion is mostly pronounced and contributes to the rapid deposition of paraffin. With the increase in the thickness of the paraffin deposit layer, the temperature rises due to the insulating effect. Consequently, the mass diffusion rate declines gradually, and at $T_{p} = WAT$(WAT– wax appearance temperature) the diffusion effect becomes insignificant.

In order to predict paraffin deposition on a cold finger, a mathematical model based on the mechanism of molecular diffusion occurring in the boundary layer was developed (Fig. 4). The diffusion rate was determined by examining the heat and mass balances, taking into account the optimal configurations of the controlled parameters. The calculation was made under the following conditions and assumptions:

• All main variables depend only on the radial coordinate (r) and time (t). Changes along the rod axis (z) are insignificant.

• Hydrodynamic calculations are based on empiric equations which were adapted to the experimental data at 350 rpm;

• The diffusion coefficient of paraffin is constant.

• Latent heat of crystallization is neglected.

Mass conductivity is calculated according to Fick’s law (15):

$$\frac{dm}{{dt}} = \left. {D\frac{\partial C}{{\partial r}}} \right|_{{R_{p} }} = \left. {D\frac{dC}{{dt}}\frac{\partial T}{{\partial r}}} \right|_{Rp} ,$$

(15)

where

D diffusion coefficient, m²/s; C concentration of dissolved paraffin in the boundary layer, kg/m³; r radial coordinate, m; $R_{p}$ radius of the paraffin deposits layer, m.

The differential equation for the heat conductivity for a cold finger system has following form (16):

$$\frac{{d^{2} T}}{{dr^{2} }} + \frac{1}{r} \cdot \frac{dT}{{dr}} = 0,$$

(16)

Boundary conditions (17):

$$\left\{ \begin{aligned} r = R_{f} \begin{array}{*{20}c} {} & {t = T_{cf} } \\ \end{array} \\ r = R_{p} \begin{array}{*{20}c} {} & {t = T_{p} } \\ \end{array} \\ \end{aligned} \right.,$$

(17)

where

$T_{f}$ cold finger’s surface temperature, °C;

$T_{p}$ temperature of the interface between oil and deposits, °C;

$R_{f}$ cold finger radius, m.

The temperature distribution in the area of paraffin deposition can be described as (18):

$$T_{1} (r,t) = T_{cf} + \frac{{T_{p} (t) - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\left( {\ln \frac{r}{{R_{f} }}} \right),$$

(18)

Similarly, the temperature distribution in the boundary layer area has following form (19):

$$T_{2} (r,t) = T_{p} (t) + \frac{{T_{bl} (t) - T_{p} (t)}}{{\ln \frac{{R_{bl} }}{{R_{p} }}}}\left( {\ln \frac{r}{{R_{p} }}} \right),$$

(19)

where

$T_{bl} (t)$ temperature of the interface between boundary layer and oil layer, ^oC;

$R_{bl}$ boundary layer radius, m.

Also, the temperature distribution in the bulk oil area is determined by (20):

$$T_{3} (r,t) = T_{bl} (t),$$

(20)

The temperatures of the wax deposits-oil interface are (21):

$$T_{p} = \frac{{T_{bl} \varphi + T_{cf} }}{\varphi + 1},$$

(21)

where

φ(T) additional function determined by following (22):

$$\varphi (t) = \frac{{\alpha_{o} R_{p} (t)}}{{\lambda_{p} }}\ln \frac{{R_{p} (t)}}{{R_{f} }},$$

(22)

The thickness of the paraffin deposit is determined by the formula (23):

$$\delta (t) = R_{f} \left( {\frac{{d(t) + 1 + \sqrt {(d(t) + 1)^{2} - 4c^{2} (t)} }}{2} - 1} \right),$$

(23)

The solubility gradient is assumed to be constant and is determined by empirical relation (24):

$$\frac{dC}{{dT}} = \beta = 1.46 \cdot 10^{ - 4} \left( {T_{f} + 17.8} \right)^{0.167} ,$$

(24)

Mass conductivity is calculated according to the Fick’s law:

$$\frac{dm}{{dt}} = \left. {D\frac{\partial C}{{\partial r}}} \right|_{{R_{p} }} = \left. {D\beta \frac{\partial T}{{\partial r}}} \right|_{Rp}$$

where

$D$ – effective diffusion coefficient in the deposits, m²/s.

Effective diffusion coefficient can be determined according to the formula (25):

$$D(,C_{p} ) = \frac{{D_{0} ()}}{{1 + \frac{{K_{\alpha }^{2} \left( {\frac{{C_{p} }}{{\rho_{p} }}} \right)^{2} }}{{1 - \frac{{C_{p} }}{{\rho_{p} }}}}}},$$

(25)

where

$K_{\alpha }$ is the dimensionless parameter that takes into account the shape of paraffin crystals in the deposits (it defines aspect ratio);

$C_{p}$ concentration of solid paraffin in the deposits, ${\rm kg/m^{3}}$; at $> WAT,C_{p} = 0$.

Interlaced crystal fibres (crystalline paraffin fibres) form a porous medium in the deposits. As a result, the diffusion coefficient of molecules is lower compared to the diffusion coefficient of molecules in oil without solid paraffin particles due to the fact that the diffusion of molecules occurs along sinuous trajectories. The diffusion coefficient of soluble paraffin is described by Gaiduk-Minhas equation (Hu et al. 2019; Zhao et al. 2017):

$D_{0} () = 13.3 \cdot 10^{ - 12} \left( {\frac{{(T + 273)^{1.47} \mu (T)^{{\frac{10.2}{{V_{A} }} - 0.791}} }}{{V_{A}^{0.71} }}} \right),$,where

T temperature, ^oC; $\mu$(T) oil viscosity in the absence of solid deposits, ${\text{mPa}}\,\, \times \,\,s$;

$V_{A}$ – molar volume of the paraffin; ${\rm cm^{3} /mol}$.

Oil viscosity in the absence of solid deposits, $\mu ()$ is determined through the Arrhenius function (Hu et al. 2019; Zhao et al. 2017):

$\mu () = 1.6 \cdot 10^{ - 2} \cdot e^{{\left( {\frac{1344}{{T + 273}}} \right)}} ,$,

As a result, the additional function determined by (26):

$$\varphi (t) = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}}\frac{{(m + C_{4} )}}{dm/dt} - 1,$$

(26)

In order to determine the kinetics of paraffin deposits formation, the dependence of the mass of deposits on time, the cold finger method is used.

Cold finger method (cold finger test)

When studying the kinetics of paraffin deposits formation, the mass of deposits (m) was considered as a time-dependent quantity. The intensity of the formation of paraffin deposit was studied through the "Cold finger test" method. 250 ml of oil was collected in a laboratory/chemical glass, with a paraffin content of 24.04% mass. At a constant temperature (T = 60 °C) and with a stirring frequency of 300 rpm measurements of the mass of deposits were made at 3, 5, 10, 15, 20, 25, 30 and 60 min. The mass was determined by removing the deposits from the surface of the finger with a scraper and further weighing them. The results of experimental studies are presented in Table 2 and Fig. 5.

Table 2 Study of the intensity of wax formation using the "cold finger" method

Fig. 5

Trend of deposits formation over time

Therefore, based on the results of experimental studies, the dependence of mass on time can be described as the following:

$$m(t) = - 3 \cdot 10^{ - 9} \cdot t^{6} + 6 \cdot 10^{ - 7} \cdot t^{5} - 4 \cdot 10^{ - 5} \cdot t^{4} + 0.0016 \cdot t^{3} - 0.0325 \cdot t^{2} + 0.3559 \cdot t + 0.0098$$

$$m^{^{\prime}} (t) = \frac{dm}{{dt}} = - 1.8 \cdot 10^{ - 8} \cdot t^{5} + 3 \cdot 10^{ - 6} \cdot t^{4} - 1.6 \cdot 10^{ - 4} \cdot t^{3} + 0.0048 \cdot t^{2} - 0.065 \cdot t + 0.3559$$

The boundary condition for Eq. (26) is obtained:

At $t = 0,\begin{array}{*{20}c} {} & {R_(t) = R_{{}} ,\varphi (0) = 0} \\ \end{array}$ it comes out:

$$\varphi (0) = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}} \cdot \frac{{C_{4} }}{{m^{^{\prime}} (0)}} - 1 \Rightarrow C_{4} = - \frac{{0.3559\rho_{op} (R_{os} - R_{f} )}}{{\alpha_{o} }},$$

(27)

Substituting condition (27) into Eq. (26), it appears (28):

$$\varphi (t) = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}} \cdot \frac{{\left( {m - \frac{{0.3559\rho_{op} (R_{os} - R_{f} )}}{{\alpha_{0} }}} \right)}}{dm/dt} - 1,$$

(28)

Therefore, the thickness of the paraffin deposit is determined by formula (29):

$$\left\{ \begin{aligned} \delta (t) = R_{f} \left( {\frac{{d(t) + 1 + \sqrt {(d(t) + 1)^{2} - 4c^{2} (t)} }}{2} - 1} \right) \\ \varphi (t) = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}} \cdot \frac{{\left( {m - \frac{{0.3559\rho_{op} (R_{os} - R_{f} )}}{{\alpha_{0} }}} \right)}}{dm/dt} - 1 \\ \end{aligned} \right.,$$

(29)

where $\frac{\varphi (t)}{a} = c(t),\begin{array}{*{20}c} {} & {a = \frac{{\alpha R_{{}} }}{\lambda }} \\ \end{array} ,\begin{array}{*{20}c} {} & {d(t) = \int {c^{^{\prime}} (t)dt} } \\ \end{array}$.

Application example and discussions

The initial parameters for the calculations are shown in Table 3.

Table 3 Initial parameters used in model calculations

During the production of high-wax oil, the thickness of the deposits increases (30), according to Eq. (8):

$$44.897\left( {\frac{{12.7 - P_{c} }}{13.7}} \right) + \frac{1308.786}{{19.4 - P_{c} }} = \frac{{1564.8 \cdot (31.7 - P_{c} )}}{{(d_{0} - 2\delta (t))^{0,5} (P_{c} - 1) \cdot \log P_{c} }},$$

(30)

Figure 6 shows the dependence of the deposits’ thickness on time.

Fig. 6

The dynamics of the thickness of paraffin deposits

The resulting dependence shows that the graph of the kinetics of paraffin deposits is gradually levelling off. The reason for this is the presence of a heat-insulating layer on the surface of the cold finger, which consists of deposited paraffin. A similar effect occurs on the surface of field equipment, when the formed deposits with low thermal conductivity reduce the temperature gradient between the surface of the deposition and the oil flow and, as a result, decrease the intensity of the deposit.

Figure 7 shows the results of the calculation of the optimal specific working agent flow rate in different moments of time, taking into account the growth of the paraffin deposits on the equipment’s surface. Well parameters are presented in Tables 1 and 2.

Fig. 7

Dependence of the effective gas factor $G_{e}$ and optimal gas flow rate $R$ on the minimum required bottom-hole pressure for various cross-sectional areas of the production tubing

During the operation of the well, the precipitation of paraffin deposits leads to a narrowing of the flow section of the tubing, the change of which was calculated as a decrease in the living section of the flow. Additional resistance contributes to an increase in the minimum required bottom-hole pressure $P_{c}$ and, according to Eq. (6), the decline in well flow rate $Q_{L}$ (Fig. 8). This leads to an increase in the demand of the specific gas flow rate at the particular value of bottom-hole pressure, which explains the shift of the $R_{o}$ curve line (Fig. 7).

Fig. 8

Dependence of the minimum required bottom-hole pressure on the thickness of the deposits

Table 4 shows the results of the calculations using Eq. (30) respective to $P_{c}$ and the corresponding values of the well production rate of oil for each considered point in time.

Table 4 Dynamics of changes in the minimum required bottom-hole pressure and well fluid flow rate

The dewaxing interval period is determined by the change in the liquid well flow rate $Q_{L}$, at the point when it falls by 20% from the initial value.

Figure 9 shows the dependence of the well flow liquid rate $Q_{L}$ on time and, according to the results obtained, the period between cleanings is supposed to be 160 h (6.67 days). The schedule of dewaxing of gas-lift wells RC is presented in the Table 5.

Fig. 9

Decrease in liquid flow rate of a gas-lift well

Table 5 Schedule of dewaxing gas-lift wells RC in 2020

Hence, a comparison of the dewaxing interval period calculated according to the proposed method and the field data (Table 5) confirms the applicability of the method and proves its accuracy.

However, a limitation of this research is that when we studied the kinetics of wax formation, degassed oil was used as a sample for experiments. In addition, the experiments were conducted under room conditions. As a result, the influence of dissolved gas and temperature was omitted, which affected the accuracy of the proposed method. In the future, we plan to build a new model to take into account the above-mentioned factors to broaden the scope of our study.

Conclusions

Most of the scientific literature to date has focused on improving the understanding of the formation process of asphaltene-resin-paraffin deposits (ARPD) and developing methods for dealing with deposits, particularly chemical methods. Nonetheless, there are no studies in the literature that specifically focus on the DIP for gas lift wells. The novelty of this paper is to develop a new mathematical model, which is of practical importance in the operation of gas lift wells with ARPD problems, specifically the determination of the dewaxing internal period (DIP) for a gas lift well. The proposed model in this paper combines several aspects of the operation of a gas-lift well into one, which now makes it possible to predict the DIP. This study draws the following conclusions:

• A mathematical model of the time-dependent wax thickness has been developed, taking into account heat and mass transfer laws and the laboratory results using the Cold Finger method. The results of this were applied to develop a comprehensive method to determine the dewaxing interval period (inter-treatment interval) for gas-lift wells in conditions of the formation of wax deposits.

• Gas lift well production fell throughout the period due to the wax formation problems that occurred during the operation of the well. The optimal dewaxing interval period is suggested to be determined by the change in the liquid well flow rate at the point when it falls by 20% from the initial value.

• The calculation of the dewaxing interval period of a gas-lift well in the Dragon field was carried out based on the developed mathematical model determining the time dependence of the wax thickness. The DIP prediction model gave a similar value to the actual DIP field data (6.67 and 6 days, respectively). This correspondence confirms the accuracy and applicability of the developed method for predicting the dewaxing interval period of the gas lift well.

• The applicability of the developed method to a larger number of wells in the Vietnam fields will be assessed in the future. In addition, to improve the complexity of the DIP prediction model, the expansion of the study scope will also be executed by taking into account additional factors that affect the wax formation during the production of gas-lift wells, such as the structure of the wax crystals connected with the features of phase transitions, flow regime, and high-pressure conditions.

Appendix- derivation of analytical solutions

Mass conductivity is calculated according to the Fick’s law (31):

$$\frac{dm}{{dt}} = \left. {D\frac{\partial C}{{\partial r}}} \right|_{{R_{p} }} = \left. {D\frac{dC}{{dt}}\frac{\partial T}{{\partial r}}} \right|_{Rp} ,$$

(31)

where

D – diffusion coefficient, m²/s;

C – concentration of dissolved paraffin in the boundary layer, kg/m³;

r – radial coordinate, m;

$R_{p}$ – radius of the paraffin deposits layer, m.

The differential equation for the heat conductivity for a cold finger system has the following form (32):

$$\frac{{d^{2} T}}{{dr^{2} }} + \frac{1}{r} \cdot \frac{dT}{{dr}} = 0,$$

(32)

Boundary conditions (33):

$$\left\{ \begin{aligned} r = R_{f} \begin{array}{*{20}c} {} & {t = T_{cf} } \\ \end{array} \\ r = R_{p} \begin{array}{*{20}c} {} & {t = T_{p} } \\ \end{array} \\ \end{aligned} \right.,$$

(33)

where

$T_{f}$ – cold finger’s surface temperature, °C;

$T_{p}$ – temperature of the interface between oil and deposits, °C;

$R_{f}$ – cold finger radius, m.

Taking $u = \frac{dT}{{dr}}$ the result is $\frac{{d^{2} T}}{{dr^{2} }} = \frac{du}{{dr}}$ and $\frac{1}{r} \cdot \frac{dT}{{dr}} = \frac{u}{r}$, after substituting into (32) it turns out (34):

$$\frac{{du}}{{dr}} + \frac{u}{r} = 0 \Leftrightarrow \ln u + \ln r = \ln C_{1} \Leftrightarrow ur = C_{1}$$

$$u = \frac{dT}{{dr}} \Rightarrow r\frac{dT}{{dr}} = C_{1} \Rightarrow dT = C_{1} \frac{dr}{r}$$

$$\Rightarrow T = C_{1} \ln r + C_{2} ,$$

(34)

When applying the boundary condition (33) to Eq. (34) the result is (35):

$$\left\{ \begin{aligned} r = R_{f} \begin{array}{*{20}c} {} & {t = T_{cf} = C_{1} \ln R_{f} + C_{2} } \\ \end{array} \\ r = R_{p} \begin{array}{*{20}c} {} & {t = T_{p} = C_{1} \ln R_{p} + C_{2} } \\ \end{array} \\ \end{aligned} \right.,$$

(35)

Therefore, free coefficients are calculated (36, 37):

$$C_{1} = \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}},$$

(36)

$$C_{2} = T_{cf} - \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\ln R_{f} ,$$

(37)

Substituting Eqs. (36) and (37) into (34), appears (38):

$$T = \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\ln r + T_{cf} - \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\ln R_{f}$$

$$\Leftrightarrow T = T_{cf} + \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}(\ln r - \ln R_{f} ) = T_{cf} + \frac{{T_{p} - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\left( {\ln \frac{r}{{R_{f} }}} \right),$$

(38)

Based on Eq. (38), the temperature distribution in the area of paraffin deposition can be described as (39):

$$T_{1} (r,t) = T_{cf} + \frac{{T_{p} (t) - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\left( {\ln \frac{r}{{R_{f} }}} \right),$$

(39)

Similarly, the temperature distribution in the boundary layer area has the following form (40):

$$T_{2} (r,t) = T_{p} (t) + \frac{{T_{bl} (t) - T_{p} (t)}}{{\ln \frac{{R_{bl} }}{{R_{p} }}}}\left( {\ln \frac{r}{{R_{p} }}} \right),$$

(40)

where

$T_{bl} (t)$ – temperature of the interface between boundary layer and oil layer, ^oC;

$R_{bl}$ – boundary layer radius, m.

Also, the temperature distribution in the bulk oil area is determined by (41):

$$T_{3} (r,t) = T_{bl} (t),$$

(41)

Taking into account the balance of the heat flux at the interface $R_{p}$, the result is (42):

$$- \lambda_{p} \frac{{\partial T_{1} (r,t)}}{\partial r} = - \lambda_{o} \frac{{\partial T_{2} (r,t)}}{\partial r},$$

(42)

Taking $dT = C_{1} \frac{dr}{r} \Rightarrow \frac{dT}{{dr}} = \frac{{C_{1} }}{r}$, it turns out (43):

$$\lambda_{p} \frac{{T_{p} (t) - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\frac{1}{{R_{p} }} = \lambda_{o} \frac{{T_{bl} (t) - T_{p} (t)}}{{\ln \frac{{R_{bl} }}{{R_{p} }}}}\frac{1}{{R_{p} }},$$

(43)

where

$\lambda_{p} ,\lambda_{o}$ – thermal conductivity of paraffin and oil, W/(m‧°C).

When assuming that the heat flux at the boundary $R_{p}$ is proportional to temperature change in the boundary layer (44):

$$\lambda_{p} \frac{{T_{p} (t) - T_{cf} }}{{\ln \frac{{R_{p} }}{{R_{f} }}}}\frac{1}{{R_{p} }} = \alpha_{o} (T_{bl} - T_{p} ),$$

(44)

where

$\alpha_{o}$ – oil heat transfer coefficient, calculated through the formula (13) and (14), $W/m^{2} \cdot K$.

Therefore, the temperatures of the wax deposits oil interface are (45):

$$T_{p} = \frac{{T_{bl} \varphi + T_{cf} }}{\varphi + 1},$$

(45)

where

φ(T) – additional function determined by following (46):

$$\varphi (t) = \frac{{\alpha_{o} R_{p} (t)}}{{\lambda_{p} }}\ln \frac{{R_{p} (t)}}{{R_{f} }},$$

(46)

Boundary condition at $t = 0,\begin{array}{*{20}c} {} & {R_{p} (t) = R_{f} ,\varphi (t) = 0} \\ \end{array}$.

If $\frac{{R_{p} (t)}}{{R_{f} }} = x \Rightarrow R_{p} (t) = R_{f} \cdot x$, it turns out (47):

$$\frac{{R_{p} (t)}}{{R_{f} }} = x \Rightarrow R_{p} (t) = R_{f} \cdot x$$

$$\varphi (t) = \frac{{\alpha_{o} R_{f} \cdot x}}{{\lambda_{p} }}\ln x,$$

(47)

Taking into account $a = \frac{{\alpha_{o} R_{f} }}{{\lambda_{p} }} \Rightarrow \varphi (t) = ax\ln x \Rightarrow x\ln x = \frac{\varphi (t)}{a}$.

If $\frac{\varphi (t)}{a} = c(t)$, the result is (48):

$$x\ln x = c(t)$$

(48)

When finding the solution of equation (48) the result is (49):

$$x\ln x = c(t)$$

$$\left( {x\ln x} \right)^{^{\prime}} = c^{^{\prime}} (t)$$

$$\frac{1}{x} \cdot x \cdot x^{^{\prime}} + \ln x \cdot x^{^{\prime}} = c^{^{\prime}} (t)$$

$$x^{^{\prime}} \cdot (\ln x + 1) = c^{^{\prime}} (t),$$

(49)

According to the (32), $\ln x = \frac{c(t)}{x}$, substituting it into (49) we get (50):

$$x^{^{\prime}} \cdot \left( {\frac{c(t)}{x} + 1} \right) = c^{^{\prime}} (t)$$

$$\frac{dx}{{dt}} \cdot \left( {\frac{c(t)}{x} + 1} \right) = c^{^{\prime}} (t)$$

$$dx \cdot \left( {\frac{c(t)}{x} + 1} \right) = c^{^{\prime}} (t)dt$$

$$\int {\left( {\frac{c(t)}{x} + 1} \right)} \cdot dx = \int {c^{^{\prime}} (t)dt}$$

$$c(t)\ln x + x = d(t) + C_{1} ,$$

(50)

where

$$d(t) = \int {c^{^{\prime}} (t)dt}$$

Putting $\ln x = \frac{c(t)}{x}$ into Eq. (50), it turns out:

$$c(t)\frac{c(t)}{x} + x = d(t) + C_{1} \Leftrightarrow \frac{{c^{2} (t)}}{x} + x = d(t) + C_{1}$$

$$x = \frac{{d(t) + C_{1} + \sqrt {(d(t) + C_{1} )^{2} - 4c^{2} (t)} }}{2}$$

$$\Rightarrow R_{p} (t) = R_{f} \cdot x = R_{f} \frac{{d(t) + C_{1} + \sqrt {(d(t) + C_{1} )^{2} - 4c^{2} (t)} }}{2}$$

The thickness of the paraffin deposit is determined by formula (51):

$$\delta (t) = R_{p} (t) - R_{f} = R_{f} \left( {\frac{{d(t) + C_{1} + \sqrt {(d(t) + C_{1} )^{2} - 4c^{2} (t)} }}{2} - 1} \right),$$

(51)

Boundary condition at $t = 0,\begin{array}{*{20}c} {} & {\delta (0) = 0} \\ \end{array} ,\begin{array}{*{20}c} {} & {c(0) = 0} \\ \end{array} ,\begin{array}{*{20}c} {} & {d(0) = 0} \\ \end{array}$, the result is (52):

$$\frac{{d(0) + C_{1} + \sqrt {(d(0) + C_{1} )^{2} - 4c^{2} (0)} }}{2} - 1 = 0$$

$$\Leftrightarrow C_{1} = 1,$$

(52)

Substituting Eq. (36) into (35), it appears (53):

$$\delta (t) = R_{f} \left( {\frac{{d(t) + 1 + \sqrt {(d(t) + 1)^{2} - 4c^{2} (t)} }}{2} - 1} \right)$$

(53)

Heat balance at $r = R_{bl}$ has the following form:

$$m = \rho V \Rightarrow dm = \rho dV = \rho d(\pi r^{2} ) = \rho 2\pi rdr$$

$$\frac{d}{{dt}}\int\limits_{{Rbl}}^{{R_{{os}} }} {\rho _{{opbl}} } dr = \left. { - \lambda _{o} \frac{{\partial T_{2} (r,t)}}{{\partial r}}} \right|_{{Rbl}}$$

where

$R_{os}$ – outer cylinder radius, m;

$_{p}$ – heat capacity of oil at constant pressure, J/(kg‧°C);

$\rho_{o}$ – oil density, kg/m³.

Assuming the change in paraffin thickness and boundary layer is negligible ($R_{bl} \approx R_{p} \approx R_{f}$), the result is (38):

$$\rho _{{op^{\prime } bl}} (R_{{os}} - R_{{bl}} ) = - \lambda _{o} \frac{{T_{{bl}} (t) - T_{p} (t)}}{{\ln \frac{{R_{{bl}} }}{{R_{p} }}}}\frac{1}{{R_{p} }},$$

(54)

Based on Eqs. (43), (44), (45) и (54), it turns out:

$$T^{^{\prime}}_{bl} = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}}\frac{{T_{bl} (t) - T_{f} }}{1 + \varphi }$$

If $b = \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}}$, it appears (55):

$$T^{^{\prime}}_{bl} = - b\frac{{T_{bl} (t) - T_{f} }}{1 + \varphi },$$

(55)

Taking into account $y = T_{bl} (t)$, the result is (56):

$$y^{^{\prime}} = - b\frac{{y - T_{f} }}{1 + \varphi }$$

$$y^{^{\prime}} + y\frac{b}{1 + \varphi (t)} = \frac{{bT_{f} }}{1 + \varphi (t)},$$

(56)

Equation $y^{^{\prime}} + y\frac{b}{1 + \varphi (t)} = 0$ gives $y = C \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }}$, if $C = C(t)$, it turns out (57):

$$y = C(t) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }}$$

$$y^{^{\prime}} = C^{^{\prime}} (t) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} - C(t) \cdot \frac{b}{1 + \varphi (t)} \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} = C^{^{\prime}} (t) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} - \frac{b}{1 + \varphi (t)} \cdot y,$$

(57)

Putting Eq. (57) into (56), it comes out:

$$C^{^{\prime}} (t) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} - \frac{b}{1 + \varphi (t)} \cdot y + \frac{b}{1 + \varphi (t)} \cdot y = \frac{{bT_{f} }}{1 + \varphi (t)}$$

$$\Leftrightarrow C^{^{\prime}} (t) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} = \frac{{bT_{{}} }}{1 + \varphi (t)} \Rightarrow C(t) = \int {\frac{{\frac{{bT_{f} }}{1 + \varphi (t)}}}{{e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} }}} \cdot dt$$

If $f(t) = \int {\frac{1}{1 + \varphi (t)}dt} \Rightarrow f^{^{\prime}} (t) = \frac{1}{1 + \varphi (t)}$, the result is:

$$C(t) = \int {\frac{{\frac{{bT_{f} }}{{1 + \varphi (t)}}}}{{e^{{ - b\int {\frac{1}{{1 + \varphi (t)}}dt} }} }}} \cdot dt \Rightarrow C(t) = bT_{f} \int {\frac{{f^{\prime } (t)}}{{e^{{ - bf(t)}} }}} {\text{ }} \cdot dt$$

Taking into account $u = e^{ - bf(t)} \Rightarrow du = - b \cdot f^{^{\prime}} (t) \cdot u \cdot dt \Rightarrow f^{^{\prime}} (t) \cdot dt = \frac{du}{{ - b \cdot u}}$, it appears (58):

$$\Rightarrow C(t) = bT_{f} \int {\frac{du}{{ - b \cdot u^{2} }}} = - T_{f} \int {\frac{du}{{u^{2} }}} = - T_{f} \left( { - \frac{1}{u} + C_{3} } \right) = \frac{{T_{f} }}{{e^{ - bf(t)} }} + C_{3}$$

$$\Rightarrow y = T_{bl} (t) = \left( {\frac{{T_{f} }}{{e^{ - bf(t)} }} + C_{3} } \right) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} = T_{f} + C_{3} \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} ,$$

(58)

Boundary condition (59):

$${\text{at}}\,t = 0,\begin{array}{*{20}c} {} & {T_{bl} (t)} \\ \end{array} = T_{os} ,\varphi (t) = 0,$$

(59)

where

$T_{os}$ – temperature outside the cylinder, ^oC.

Substituting condition (59) into expression (58), the result is (60):

$$T_{os} = T_{f} + C_{3} \Rightarrow C_{3} = T_{os} - T_{f} ,$$

(60)

Putting condition (60) into Eq. (58), we get (61):

$$T_{bl} (t) = T_{f} + (T_{os} - T_{f} ) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} ,$$

(61)

The solubility gradient is assumed to be constant and is determined by empirical relation (62):

$$\frac{dC}{{dT}} = \beta = 1.46 \cdot 10^{ - 4} \left( {T_{f} + 17.8} \right)^{0.167} ,$$

(62)

Mass conductivity is calculated according to the Fick’s law:

$$\frac{dm}{{dt}} = \left. {D\frac{\partial C}{{\partial r}}} \right|_{{R_{p} }} = \left. {D\beta \frac{\partial T}{{\partial r}}} \right|_{Rp}$$

where

$D$ – effective diffusion coefficient in the deposits, m²/s.

Effective diffusion coefficient can be determined according to the formula (63):

$$D(,C_{p} ) = \frac{{D_{0} ()}}{{1 + \frac{{K_{\alpha }^{2} \left( {\frac{{C_{p} }}{{\rho_{p} }}} \right)^{2} }}{{1 - \frac{{C_{p} }}{{\rho_{p} }}}}}},$$

(63)

where

$K_{\alpha }$ – is the dimensionless parameter that takes into account the shape of paraffin crystals in the deposits (it defines aspect ratio);

$C_{p}$ – concentration of solid paraffin in the deposits, $kg/m^{3}$; at $> WAT,C_{p} = 0$.

The diffusion coefficient of soluble paraffin is described by Gaiduk-Minhas equation (Hu et al. 2019; Zhao et al. 2017):

$D_{0} () = 13.3 \cdot 10^{ - 12} \left( {\frac{{(T + 273)^{1.47} \mu (T)^{{\frac{10.2}{{V_{A} }} - 0.791}} }}{{V_{A}^{0.71} }}} \right),$ where T – temperature, ^oC;

$\mu$(T) – oil viscosity in the absence of solid deposits, $mPa \cdot s$;

$V_{A}$ – molar volume of the paraffin; $cm^{3} /mol$.

Oil viscosity in the absence of solid deposits, $\mu (T)$ is determined through the Arrhenius function (Hu et al. 2019; Zhao et al. 2017):

$\mu (T) = 1.6 \cdot 10^{ - 2} \cdot e^{{\left( {\frac{1344}{{T + 273}}} \right)}} ,$,

From Eq. (44) gives:

$$\frac{dm}{{dt}} = \left. {D\frac{\partial C}{{\partial r}}} \right|_{{R_{p} }} = \frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}\left( {T_{bl} (t) - T_{p} (t)} \right),$$

(64)

From Eq. (45) $T_{p} = \frac{{T_{bl} \varphi + T_{cf} }}{\varphi + 1}$, it comes (65):

$$\frac{dm}{{dt}} = \frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}\left( {T_{bl} (t) - \frac{{T_{bl} (t)\varphi + T_{cf} }}{\varphi + 1}} \right)$$

$$\Leftrightarrow \frac{dm}{{dt}} = \frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}\left( {\frac{{T_{bl} (t) - T_{cf} }}{\varphi + 1}} \right),$$

(65)

From Eq. (45) $\Rightarrow T_{bl} (t) - T_{f} = (T_{os} - T_{f} ) \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }}$, putting into Eq. (65), it comes out (66):

$$\frac{dm}{{dt}} = \frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}\left( {\frac{{T_{bl} (t) - T_{cf} }}{\varphi (t) + 1}} \right) = \frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}\frac{{(T_{os} - T_{f} )}}{\varphi (t) + 1} \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} ,$$

(66)

Applying $\frac{{D\beta \alpha_{o} }}{{\lambda_{p} }}(T_{os} - T_{f} ) = G$ and substituting into Eq. (65), the result is (67):

$$h(t) = \frac{dm}{{dt}} = \frac{G}{\varphi (t) + 1} \cdot e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} ,$$

(67)

Therefore, there is an algebraical expression (68):

$$\left( {e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} } \right)^{^{\prime}} = e^{{ - b\int {\frac{1}{1 + \varphi (t)}dt} }} \cdot \frac{ - b}{{1 + \varphi (t)}},$$

(68)

Based on Eqs. (67) and (68) it appears (69):

$$h(t) = \frac{{dm}}{{dt}} = \frac{G}{{ - b}} \cdot \left( {e^{{ - b\int {\frac{1}{{1 + \varphi (t)}}dt} }} } \right)^{{\prime }} \Rightarrow e^{{ - b\int {\frac{1}{{1 + \varphi (t)}}dt} }} = \frac{{ - b}}{G} \cdot \int {h(t)} dt$$

$$\Leftrightarrow \int {\frac{1}{1 + \varphi (t)}dt} = - \frac{1}{b}\ln \left( {\frac{ - b}{G} \cdot \int {h(t)} dt} \right),$$

(69)

Derivatives of both sides of Eq. (69) give (70):

$$\frac{1}{{1 + \varphi (t)}} = - \frac{1}{b}\left( {\ln \left( {\frac{{ - b}}{G} \cdot \int {h(t)} dt} \right)} \right)^{{\prime }} \Leftrightarrow \frac{1}{{1 + \varphi (t)}} = - \frac{1}{b}\frac{{\left( {\frac{{ - b}}{G} \cdot \int {h(t)} dt} \right)}}{{\left( {\frac{{ - b}}{G} \cdot \int {h(t)} dt} \right)}}^{{\prime }}$$

$$\Leftrightarrow \frac{1}{1 + \varphi (t)} = - \frac{1}{b}\frac{h(t)}{{\int {h(t)} dt}},$$

(70)

Substituting $h(t) = \frac{dm}{{dt}}$ into (70), it comes out (71):

$$\frac{1}{1 + \varphi (t)} = - \frac{1}{b}\frac{{\frac{dm}{{dt}}}}{{\int {\frac{dm}{{dt}}dt} }} = - \frac{1}{b}\frac{{\frac{dm}{{dt}}}}{{m + C_{4} }}$$

$$\Rightarrow \varphi (t) = - \frac{{b \cdot (m + C_{4} )}}{dm/dt} - 1,$$

(71)

Substituting $b = \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{cf} )}}$ into Eq. (66), the result is (72):

$$\varphi (t) = - \frac{{\alpha_{o} }}{{\rho_{op} (R_{os} - R_{f} )}}\frac{{(m + C_{4} )}}{dm/dt} - 1,$$

(71)