Introduction

The success of oil and gas well drilling operation is highly dependent on the selection and design of an appropriate drilling fluid. Generally, the expenditure of drilling fluid in a drilling operation ranges from 5 to 15%, but it may potentially cause significant drilling challenges (Smith et al. 2018; Agwu et al. 2018). The three main broad categories of drilling fluids are water-based mud (WBM), oil-based mud (OBM) and synthetic-based mud (SBM). WBM is commonly preferred amongst the other types due to its economic advantage, lower toxicity, and lower waste and environment challenges (Mahmoud et al. 2016; Smith et al. 2018). Drilling fluid has diverse functions in a drilling operation such as circulating drill cuttings and acting as the primary barrier for well control by exerting hydrostatic pressure on the formation. It also suspends the drill cuttings during a drilling break, cools and lubricates the drill bit, and maintains the wellbore stability in uncased section (Agarwal et al. 2011; Alvi et al. 2018).

Rheological properties of drilling fluid are critical to achieve an optimum drilling performance as it affects the hole cleaning process and rate of penetration in drilling (Gowida et al. 2019). Losing the basic required mud rheology such as plastic viscosity (PV), yield point (YP), and gel strength (GS) may lead to the occurrence of severe drilling complications (Abdo and Haneef 2013). Drilling fluid that penetrates the permeable formation or the fluid loss will result in an invasion process and the formation of mud cake. It is crucial to mitigate an excessive fluid loss into formation as it will lead to formation of damage and affect the productivity and injectivity of a well (Contreras et al. 2014). Additives such as polymers and bentonite clay are commonly added in drilling fluid to function as a rheology modifier and fluid loss controller in drilling fluid. However, some weighting material and the polymeric additives tend to undergo degradation or breakdown at high-temperature condition, and it results in varying drilling mud rheology (Agarwal et al. 2011). According to Zakaria et al. (2012), conventional usage of a macro- or micro-drilling fluid often failed to reduce the fluid loss due to its size and limited functional ability.

Since the emergence of nanotechnology in the past decade, there were numerous experimental studies and research on the advantages of several nanoparticles on conventional drilling fluid. Silica (SiO2) can be found abundantly in sand or quartz; it is one of the most commercialised nanoparticles due to its well-known preparation method (Riley et al. 2012). Recent research by Keshavarz Moraveji et al. (2020) showed that SiO2 nanoparticles had improved the apparent viscosity, plastic viscosity and yield point of drilling mud compared to the base fluid. The thermal stability of the drilling fluid is improved proven by the less severe reduction in rheological behaviour after the hot rolling process in the presence of nanoparticles. The filtration loss (FL) of the drilling fluid also reduced with the increasing weight fraction of nanoparticles. A flow loop experiment conducted by Gbadamosi et al. (2019) using SiO2 nanoparticle water-based drilling fluid demonstrated an improvement in borehole cleaning efficiency indicated by the increase in lifting efficiency of 13%. The enhancement in the drilling fluid rheology has enabled a better suspension and transport of cuttings to the surface. Mao et al. (2015) found that nanoparticle-assisted drilling fluid can effectively plug the micro-pores and micro-cracks through cross-linking and bridging. The formation of thin but dense mud cake aids to minimise the mud filtration loss as well as improve the pressure bearing capability of formation. Nanoparticles with ultra-fine sizes minimise the issue of accessing micropores or surfaces of the near-wellbore formations (Vryzas et al. 2015). According to Mao et al. (2015), SiO2 in nano-scale exhibit high surface energy, rigidity, thermal and dimensional stability. It can function efficiently and effectively, along with the presence of other foreign molecules such as Acrylamide, sulfonic acid, Maleic anhydride, and Styren. Table 1 summarises the other applications of nanoparticles in the water-based drilling fluid. The effect of SiO2 on drilling fluids had been extensively investigated showing positive results to rheological behaviour and filtration properties.

Table 1 Previous studies of the application of nanoparticle in water-based drilling fluid
Full size table

Recently, artificial intelligence (AI) has aroused attention and adaptability in the oil and gas industry. Machine learning, as a subset of AI, is defined as a technique that is capable of processing multifaceted attributes from a historical database to deal with nonlinear problems for prediction and generalisation with high efficiency (Bello et al. 2015). As drilling is one of the most expensive operations in the industry, AI is reported in numerous studies as a proficient solution to reduce drilling cost (Bello et al. 2015). Artificial neural network (ANN), fuzzy logic, support vector machines (SVM), hybrid intelligent system (HIS), case-based reasoning (CBR) are some popular implementations in machine learning. According to the review by Agwu et al. (2018), both ANN and SVM have been utilised in the prediction of rheological properties and filtration loss with promising results. However, the predictions performed only account for conventional drilling fluid without the inclusion of nanoparticles. Artificial neural network (ANN) was the first AI tool to be implemented in the oil and gas industry, and it is one of the most employed techniques of AI (Popa and Cassidy 2012). Other than the prediction of rheology and filtration loss, ANN has been applied in prediction of mud density, lost circulation, mudflow pattern, hole cleaning, cutting transport efficiency, settling velocity of cuttings and frictional pressure loss (Osman and Aggour 2003; Ozbayoglu and Ozbayoglu 2007; Al-Azani et al. 2019; Alkinani et al. 2020; Alanazi et al. 2022). The feed-forward multilayer perceptron (FFMLP) architecture, paired with a back-propagation learning algorithm, is the most widely used ANN. Most networks comprised of one hidden layer adopting Levenberg–Marquardt (LM) as the optimisation method for weights and biases. The application of LM algorithm in ANN has demonstrated to outperform other algorithms such as Scaled Conjugate Gradient and Resilient Back-Propagation due to its fast and stable convergence (Sapna 2012; Du and Stephanus 2018; Yu and Wilamowski 2018; Liu et al. 2020). According to Yu and Wilamowski (2018), this algorithm is more robust and efficient in training small and medium-sized problem. It is noticeable that most of the predictions involve a conventional drilling fluid, and there are limited studies that involve the application of nanoparticles in drilling fluid. Table 2 shows the application of ANN in drilling fluids.

Table 2 Previous studies of ANN applications in drilling fluid
Full size table

The application of LSSVM in the oil and gas industry is less prominent compared to the long-established ANN. Least square support vector machine (LSSVM), proposed by Suykens and Vandewalle in 1999, is an improvised machine learning approach of SVM that was developed by Cortes and Vapnik in 1995 (Chen et al. 2020). The SVM incorporates the idea of mapping nonlinear inputs from the primal to a higher dimensional space through a kernel function. The primary advantage of SVM compared to an ANN is that the computation process does not require hidden nodes, and it has fewer parameters to be optimised (Ghorbani et al. 2020). It has a better generalisation and a lower tendency to overfit. The quadratic programming algorithm in SVM involves variables subjected to linear constraints, commonly results in a more rapid convergence than ANN. However, SVM has a major downside due to its model complexity and required constrained optimisation programming that may cause a longer computation time (Wang and Hu 2005). The introduction of LSSVM has increased the efficiency and accuracy of a traditional SVM by using a sum-squared-error cost function which is a form of a linear system known as Karush–Kuhn–Tucker (KKT) instead of inequality constraints which is quadratic (Wang and Hu 2005; Asadi et al. 2021). Similar to SVM, LSSVM transforms the data from its defined dimension to a higher dimensional space to convert a nonlinear problem to be approximately linear (Ma et al. 2018). Radial basis function, also known as Gaussian, is the most capable and widely used kernel among the other kernels such as linear and polynomial. (Wang and Hu 2005; Ma et al. 2018; Uma Maheswari and Umamaheswari 2020). Table 3 summarises the studies of LSSVM in drilling operations.

Table 3 Previous studies of LSSVM applications in oil and gas industry
Full size table

Drilling fluid is a non-Newtonian fluid that violates the Newton’s Law of Viscosity where the shear stress is not proportional to the shear rate applied. The rheology of a non-Newtonian drilling fluid can be described by the Bingham Plastic, Herschel–Bulkley and Power Law fluid model. The most widely used model, Bingham Plastic is a two-parameters rheological model. Based on a Bingham Plastic fluid shear stress versus shear rate graph, the intersection point depicts the yield point, and the slope represents the plastic viscosity of a fluid. The pioneer analytical model to estimate the viscosity of mixtures or composites was developed by Einstein (1906). Modified models were proposed based on the Einstein model namely Brinkman model, Batchelor model and Graham model, mainly considering the interfacial layer on the nanoparticle (Udawattha et al. 2019). A correlation to determine nanofluid viscosity based on Brownian motion of nanoparticle developed in 2009, but it was contended to be negligible in 2016 (Masoumi et al. 2009; Moratis 2016). Researchers later started to discover the impact of temperature, size of particle, and concentration on viscosity through experiments (Udawattha et al. 2019). However, no exact correlation can provide the viscosity of nanofluids over a wide range of concentration. The static filtration behaviour of drilling fluid is determined through a static filter press test by applying a differential pressure at elevated temperature to simulate the borehole condition according to API specifications.

Mud formulations are often determined from laboratory experiments through trial and errors depending on the experience of the mud engineer to achieve the desirable properties (Shadravan et al. 2015). Laboratory experiments are time-consuming and expensive to conduct over a wide range of controlling parameters as it involves the preparation of base fluid and nanoparticles, dispersion and stabilisation of the nanoparticles in the solvent to achieve a favourable result (Shahsavar et al. 2019). Therefore, the incorporation of machine learning is essential in developing a system that utilises the available data and trends from past cases which will provide better insight for the mud engineer to increase efficiency and reduces the cost of experimenting. This research aimed to develop two machine learning models using ANN and LSSVM to predict the shear stress and filtration volume of SiO2 nanoparticle water-based drilling fluid. The network performance for each prediction is evaluated by statistical parameters such as the coefficient of determination (R2), root mean square error (RMSE), mean absolute percentage error (MAPE) and mean absolute error (MAE). The trend of predicted shear stress and filtration loss at varying input parameters is validated with the experimental trendline to gain intuition on the dependency of the outputs on the controlling factors.

Methodology

Data acquisition and normalisation

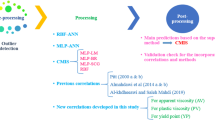
The foundation of a machine learning model is established based on historical data. To date, there are an appreciable number of experimental studies to examine the effect of SiO2 nanoparticles on the properties of water-based drilling fluid with different variables. Figure 1 is the overall flowchart of the methodology adopted in this research work.

Fig. 1
figure 1

General workflow to develop the machine learning models

Full size image

The input parameters utilised for the prediction of shear stress include shear rate, nanoparticle concentration and temperature. One hundred fifty-six (156) data points are gathered from three (3) published experimental results (Vryzas et al. 2015; Mahmoud et al. 2016, 2018). The WBM formulation for all the studies contained seven (7) wt% bentonite prepared according to the requirement of API Specifications 13A. The nano-silica used in all studies had an average size of 12 nm. The experiment was conducted at varying nanoparticles concentration from 0 to 2.5 wt% and temperature from 78 °F to 200 °F at atmospheric pressure. The shear stress of the drilling fluid was measured at shear rates ranges in 4 s−1 to 1200 s−1.

Two hundred fifty-four (254) data points comprised of nanoparticle concentration, temperature and time from another published literature have contributed as the inputs for the prediction of filtration loss (Parizad et al. 2018). The average grain size for the SiO2 nanoparticles used in this research range from 10 to 15 nm. The filtration loss of SiO2 nanoparticle drilling fluid was measured by conducting API filtration test at a varying concentration from 0 to 7.5 wt% and temperature from 77 °F to 199.4 °F at a fixed differential pressure of 100 psig. The filtration volume was recorded at a different interval within 30 min. Tables 4 and 5 are the statistical descriptions of the datasets for the prediction of shear stress and filtration volume, respectively.

Table 4 Statistical description of databank for prediction of shear stress
Full size table
Table 5 Statistical description of databank for prediction of filtration volume
Full size table

All data parameters are normalised based on the minimum and maximum value according to Eq. (1). Data normalisation is a good practice prior to training to adjust the data distribution so that the mean of all data points is close to zero (Razi et al. 2013; Liu et al. 2020). Normalised data can increase the efficiency of training and speed up the network convergence. The illustrations of data distribution for prediction of shear stress and filtration loss after normalisation are shown in Fig. 2 and Fig. 3, respectively.

Fig. 2
figure 2

Distribution of normalised data for prediction of shear stress

Full size image
Fig. 3
figure 3

Distribution of normalised data for prediction of filtration loss

Full size image

The data points marked beyond the minimum and maximum line indicate the outliers. Generally, the filtration loss datasets have a better quality than shear stress as there were ten (10) outliers out of 156 data of experimental shear stress values. For the experimental of filtration loss, there were only two (2) outliers out of 254 data points.

$$\begin{array}{*{20}c} {x_{{\text{n }}}^{^{\prime}} = \frac{{x - x_{{{\text{min}}}} }}{{x_{{{\text{max}}}} - x_{{{\text{min}}}} }}} \\ \end{array}$$
(1)

Artificial neural network (ANN)

Every artificial neuron comprises multiplication, summation and activation function represented by the mathematical model in Eq. 2. Multiple artificial neurons must be combined to harvest the capability of an ANN completely. There are several possible ways to connect the neurons, and the terminology to describe the interconnection of neurons is known as topology or architecture. A multilayer feed-forward ANN architecture where information generally flows in a forward direction from input to output is employed in this research. The activation function for the input layer and hidden layers follows the nonlinear function, whereas the linear activation function is selected for the output layer to assure the outcome to be in the acceptable range. Tansig (Hyperbolic tangent sigmoid function) is employed as an activation function for input and hidden layer, and Purelin (Linear transfer function) is used as an activation function for the output layer. Figure 4 and Fig. 5 illustrate the architecture of ANN for the prediction of shear stress and filtration loss, respectively.

$$\begin{array}{*{20}c} {y = F \left( {\mathop \sum \limits_{i = 0}^{n} w_{{\text{i}}} \cdot x_{{\text{i}}} + b} \right)} \\ \end{array}$$
(2)
Fig. 4
figure 4

ANN architecture for prediction of shear stress

Full size image
Fig. 5
figure 5

ANN architecture for prediction of filtration volume

Full size image

where \(y\) is the output, \(x\) is the input, \(w\) is the weight, \(b\) is the bias, \(i\) is the data index, and \(n{ }\) is the total number of data points. The initial weight of the ANN model is selected randomly in the range of \(\left( {\frac{ - 1}{{\sqrt {i_{{\text{n}}} } }},\frac{1}{{\sqrt {i_{{\text{n}}} } }}} \right)\), where ‘in’ is the total input to a neuron.

ANN model may consist of single or multiple hidden layers depending on the complexity of the problem and optimisation process. The presence of hidden layers with neurons provides an extrasynaptic connection and dimension of neural interactions (Cohen 1994). A trial-and-error approach by manipulating the number of hidden layers and neurons is adopted to finalise a topology best suited for the predictions. The loss/error function is set to the root mean square error (RMSE). The RMSE depicts the error in the new developed model by indicating the deviation between actual data and predicted data. This error is used to evaluate and compare the different ANN architecture with varying neurons and hidden layer to determine the best topology. An optimal number of neurons in the hidden layers is vital to avoid underfitting or overfitting due to excessive or insufficient neurons. A back-propagation learning algorithm Levenberg–Marquardt is used to optimise the weights and biases. The entire model is established using a simulation tool, MATLAB (R2020a).

The proportion of the training, validation, and testing vectors for the construction of ANN to predict shear stress and filtration volume is 70:15:15 and 80:10:10, respectively. The validation datasets act as the stopping criteria of a training process. The network training will halt if the performance of the validation samples failed to improve or remains for six (6) consecutive epochs in a row. Mean square error (MSE) is the indicator of the improvement in the prediction.

Least square support vector machine (LSSVM)

The LSSVM network has a simpler architecture as it involves fewer tuning parameters and no hidden nodes involved compared to ANN. According to Asadi et al. (2021), the linear form of the input and output vectors in an LSSVM model can be generally represented by Eq. 3 where \(\varphi\) is the mapping of inputs, \(X_{{\text{i}}}\) to a higher dimension. The weight, W and bias, b are determined from the cost function in Eq. 4 in which a regularisation parameter, gamma (γ), is involved. A final form of LSSVM is shown in Eq. 5 which \(K\) features the kernel trick to be applied in the LSSVM model. Radial basis function will be the kernel trick in this research, and it is formulated in Eq. 6, where sigma (\(\sigma )\) is the kernel parameter to be optimised.

$$\begin{array}{*{20}c} {y_{{\text{i}}} = w^{T} \cdot \varphi \left( {y_{{\text{i}}} } \right) + b} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {Cost Function = \frac{1}{2}w^{T} w + \frac{\gamma }{2}\mathop \sum \limits_{{{\text{i}} = 1}}^{n} e_{{\text{i}}}^{2} } \\ \end{array}$$
(4)
$$\begin{array}{*{20}c} {y_{{\text{i}}} = \mathop \sum \limits_{i = 1}^{n} a_{{\text{i}}} K\left( {x_{{\text{i}}} \cdot x_{{\text{j}}} } \right) + b} \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {K\left( {x_{{\text{i}}} .x_{{\text{j}}} } \right) = \exp \left[ { - \frac{{\left| {x_{{\text{i}}} - x_{{\text{j}}} } \right|^{2} }}{{2\sigma^{2} }}} \right] } \\ \end{array}$$
(6)

The proportion of training for the testing dataset in the LSSVM model to predict shear stress and filtration volume has a ratio of 80:20 and 70:30, respectively. The tuning parameters, which includes the kernel (σ2) and regularisation (γ) parameter, are optimised by the Couple Simulated Annealing (CSA) algorithm. CSA is a modified technique from simulated annealing (SA) that exhibits a higher convergence speed and accuracy (Dashti et al. 2020; Ghorbani et al. 2020). The best-optimised parameters are finalised after an iterative process of training, testing and performance evaluation. Figure 6 and Fig. 7 exhibit the LSSVM architecture for prediction of shear stress and filtration volume, respectively.

Fig. 6
figure 6

LSSVM architecture for prediction of shear stress

Full size image
Fig. 7
figure 7

LSSVM architecture for prediction of filtration volume

Full size image

Model performance evaluation

The statistical parameters used to evaluate the performance or accuracy of the network are the coefficient of determination (R2), root mean square error (RMSE) and mean absolute percentage error (MAPE) and mean absolute error (MAE). These values are computed for all the predicted output from training, validation and testing. R2 measures how close the outputs are fitted to the target values. RMSE, MAPE and MAE depict the difference between the experimental and predicted values. R2 value close to 1 or a low value of RMSE, MAPE and MAE indicates a favourable prediction result. R2, RMSE, MAPE and MAE are expressed mathematically as Eq. (7) to (10), respectively, where, \(y_{{\text{i}}}^{A}\) is the original used data and \(y_{{\text{i}}}^{p}\) is the predicted data.

$$\begin{array}{*{20}c} {R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{i = n} \left( {y_{{\text{i}}}^{A} - y_{{\text{i}}}^{P} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{i = n} \left( {y_{{\text{i}}}^{Actual} - \overline{y}} \right)^{2} }}} \\ \end{array}$$
(7)
$$\begin{array}{*{20}c} {{\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{i = n} (y_{{\text{i}}}^{A} - y_{{\text{i}}}^{P} )} } \\ \end{array}$$
(8)
$$\begin{array}{*{20}c} {{\text{MAPE}}\left( {\text{\% }} \right) = \frac{100}{n}\mathop \sum \nolimits_{i = 1}^{i = n} \left| {\frac{{y_{{\text{i}}}^{A} - y_{{\text{i}}}^{P} }}{{y_{{\text{i}}}^{Actual} }}} \right|} \\ \end{array}$$
(9)
$$\begin{array}{*{20}c} {{\text{MAE}} = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{i = n} \left| {y_{{\text{i}}}^{A} - y_{{\text{i}}}^{P} } \right|} \\ \end{array}$$
(10)

Results and discussion

Prediction of shear stress

Artificial neural network (ANN)

Twenty (20) iterations were performed by manipulating the number of the hidden layer(s) from 1 to 2 and the number of hidden node(s) from 1 to 50. The network configuration with the lowest overall RMSE is the optimum network architecture, and its topology will be selected for further prediction. Figure 8 plots the RMSE of the predicted training, validation and testing outputs obtained from the best iteration. Based on the plots, the increase in neurons does not guarantee an increase in accuracy as weight and biases are continually changing in every run. Table 6 quantifies the RMSE and R2 of the best quantity of hidden neuron(s) using 1 and 2 hidden layer(s). The overall RMSE and R2 values are averaged from the RMSE and R2 values of training, validation and testing vectors. A well-tuned model should be capable of yielding high accuracy for the prediction of all the training, validation and testing vectors without jeopardising the accuracy of one another. Based on Table 6, one (1) hidden layer generally performed better than the two (2) hidden layers networks as it has a lower RMSE and higher R2 values. The best performance is achieved with one (1) hidden layer consisting of 18 hidden nodes with an overall RMSE of 2.0235 lbf/ft2 and R2 of 0.9924. Therefore, a topology of 3–18-1 is selected for the prediction of shear stress.

Fig. 8
figure 8

RMSE of ANN for prediction of shear stress

Full size image
Table 6 Statistics of ANN predicted shear stress for 1 and 2 hidden layers
Full size table

The weights and biases of every neuron optimised by LM algorithm are extracted from the finalised network configurations for further training, validation and testing process. Figure 9 shows the MSE at every epoch for the prediction of shear stress. Epoch is the measure of how many times the training vectors are passed back from the output layer to update the weights and biases. The best result for the validation dataset is achieved at zeroth epoch with the lowest MSE of 0.24453 lbf/ft2. Since there is no noticeable improvement for six (6) consecutive epochs, the stopping criterion is triggered, and the training cycle is ceased. Based on Fig. 9, MSE for all the train, validation and test vectors stabilises after the fourth epoch, this is where the network found the optimal solution for the weights and biases.

Fig. 9
figure 9

MSE at different epochs of ANN for prediction of shear stress

Full size image

Figure 10 shows the parity plots of the predicted outputs versus actual shear stress. The training, validation and testing R2 values are 0.993, 0.998 and 0.999, respectively. The coefficient of determination of both test and validation vectors exceeds 0.995, although training data sets yield a slightly lower value. The R2 infers that the network has an excellent generalisation to the new testing data points and does not overfit. The calculated RMSE based on the predicted and experimental outputs from training, validation, testing is 2.029 lbf/ft2, 0.495 lbf/ft2, and 0.466 lbf/ft2.

Fig. 10
figure 10

Parity plots of ANN for prediction of shear stress: a Overall Data b Training Data c Validation Data d Testing Data

Full size image

A graphical plot of the error distributions is presented in Fig. 11 to demonstrate the error in the prediction of the developed ANN model. Based on the plot, the maximum relative error between the predicted and actual shear stress ranges from about − 40 to 30%.

Fig. 11
figure 11

Relative error of ANN for prediction of shear stress

Full size image

Least square support vector machine (LSSVM)

Twenty (20) iterations with 100 runs each were performed to determine the radial basis function kernel parameter (σ) and regularisation parameter (γ). These parameters are initialised randomly and optimised by CSA. The best performance from each iteration is ranked based on the lowest RMSE, and the results are plotted in Fig. 12. Based on the figure, the 16th iteration yields the lowest overall RMSE with a value of 1.452 lbf/ft2. The kernel and the regularisation parameters are acquired from the optimal iteration with the values of 1.5706e + 05 and 13.5046.

Fig. 12
figure 12

RMSE of LSSVM for prediction of shear stress

Full size image

The RMSE of prediction of shear stress for training and testing datasets is 1.696 lbf/ft2 and 1.209 lbf/ft2. Figure 13 (a–c) shows the parity plots for the training and testing vectors of prediction of filtration volume with R2 of 0.994 and 0.995, respectively. The R2 values, which are very close to 1.0, demonstrate the capability of LSSVM to predict the shear stress accurately. The reasonably low RMSE and high R2 of testing datasets proved the model has a low tendency to overfit the training vectors. The relative error is plotted in Fig. 13 (d). The predicted output deviates with a maximum relative error from − 18.2 to 26.8%.

Fig. 13
figure 13

Parity plots of LSSVM for prediction of shear stress: a Overall Data b Training Data c Testing Data; d Relative error of LSSVM for prediction of shear stress

Full size image

Prediction of filtration volume

Artificial neural network (ANN)

The methodology to determine the architecture for prediction of filtration loss is similar to the approach in prediction of shear stress. Figure 14 shows the plot of the lowest RMSE generated from 1 to 50 neurons from ANN comprised of 1 and 2 hidden layers. It can be observed that one (1) hidden layer network generally outperforms two (2) hidden layers networks for the majority number of hidden nodes. As referred to Table 7, the network with (1) hidden layer and 24 hidden nodes yields the best prediction results with RMSE of 0.2103 mL and R2 of 0.9993. Therefore, the final network architecture of ANN for prediction of filtration volume is determined to be 3–24-1.

Fig. 14
figure 14

RMSE of ANN for prediction of filtration volume

Full size image
Table 7 Statistics of ANN predicted filtration volume for 1 and 2 hidden layers
Full size table

The best validation performance is achieved with MSE of 0.04844 mL at epoch 15, as observed from Fig. 15. The RMSE computed based on the predicted outputs is 0.115 mL, 0.220 mL and 0.195 mL for the training, validation and testing datasets. As compared to the prediction of shear stress, the network for the prediction of filtration volume consumed more computation steps as the curves flatten after 18 epochs. The trendline of MSE before the tenth epoch indicates the network is prone to underfit as the MSE of the training vector is relatively high compared to the MSE after the fifteenth epoch.

Fig. 15
figure 15

MSE at different epochs of ANN for prediction of filtration volume

Full size image

Figure 16 shows the parity plots for different data environments. The predicted outputs are mostly overlying with the designated slope at R2 = 1; this indicates that the prediction is highly accurate. The R2 values for all the training, validation and testing are 0.9998, 0.9994 and 0.9993. According to Fig. 17, the relative errors of predicted output for filtration loss are relatively lower compared to the prediction of the shear rate as the maximum relative error lies between − 12.7 and 23.5%.

Fig. 16
figure 16

Parity plots of ANN for prediction of filtration volume: a Overall Data b Training Data c Validation Data d Testing Data

Full size image
Fig. 17
figure 17

Relative error of ANN for prediction of filtration volume

Full size image

Least square support vector machine (LSSVM-FV)

The approach to select the kernel parameters in the prediction of shear stress is adopted in this section. Figure 18 shows that the 7th iteration yields the lowest RMSE with a value of 0.231 ml. The kernel and regularisation parameters at this iteration are 1.2484e + 08 and 66.8216.

Fig. 18
figure 18

RMSE of LSSVM for prediction of filtration volume

Full size image

The computed RMSE values from the prediction of filtration volume using LSSVM are 0.2309 mL and 0.2308 mL for training and testing vectors. The R2 values are 0.9992 and 0.9991 for the training and testing, respectively. The low RMSE and high R2 obtained for all vectors demonstrate the capability of LSSVM with a low tendency to overfit or underfit in the training process. Lastly, the percentage of relative error for each predicted output corresponding to the actual value is calculated and plotted in the following figure. The relative error of the predicted filtration loss lies between − 8.1 and 38.6%, as shown in Fig. 19.

Fig. 19
figure 19

Parity plots of LSSVM for prediction of filtration volume: a Overall Data b Training Data c Testing Data; d Relative error of LSSVM for prediction of filtration volume

Full size image

Analysis of outlier effect

Effect of outlier on the developed model is determined by analysing the William’s plot. It is a graphical representation of standardised residuals (R) and leverage value. The leverage value variation in these plots is used to describe the outlier impact on model. Leverage values are defined as the data with extreme value of the predictor dataset (x). It is represented mathematically as Eq. (11).

$$\begin{array}{*{20}c} {H_{{\text{i}}} = x_{{\text{i}}}^{T} \left( {X^{T} X} \right)^{ - 1} x_{{\text{i}}} } \\ \end{array}$$
(11)

where, Hi is the hat matrix (also known as projection matrix), xi is the selected datapoint from the descriptive vector and X is the matrix from the training data descriptor values. The William’s plot of all the developed models is presented in Fig. 20. Grubbs critical T value is used to separate the outlier from the valid data points on y-axis. It can be calculated using Eq. (12). The Grubbs critical T value for shear stress data is 3.91 and 4.05 for filtration volume data. The normalised leverage value is used in Fig. 20. Hence, the average of leverage is 1. Therefore, the leverage limit is arbitrarily selected the double of leverage average that is the value of 2 on x-axis. The leverage limit is used to separate high leverage value from the dataset. In Fig. 20, a square area is formed using Grubbs critical T value and leverage limit. This square area is known as applicability domain. The developed models are deemed a statistically valid model when most of the data are in this domain. As illustrated in this figure, majority of the datapoints are spotted in the applicability domain area which indicates that the models developed using ANN and LSSVM for shear stress and filtration volume prediction are reliable.

$$\begin{array}{c} {G = \frac{{\left( {n - 1} \right)}} {\sqrt n } \sqrt {\frac{{\left( {t_{{\alpha /\left( {2n} \right), n - 3}} } \right)^{2} }}{{n - 3 + \left( {t_{{\alpha /\left( {2n} \right), n - 3}} } \right)^{2} }}} } \end{array}$$
(12)
Fig. 20
figure 20

William’s plots of ANN and LSSVM for prediction of shear stress (SS) and filtration volume (FV)

Full size image

where, G is the Grubbs critical T value, (n-3) is the degree of freedom and α/(2n) represents the significance level.

Comparison of ANN and LSSVM

Both applications of ANN and LSSVM showed acceptable and accurate results in predicting the shear stress and filtration loss of SiO2 nanoparticles water-based drilling fluid. Table 8 and Table 9 summarise the RMSE, R2, MAE and MAPE of the developed model. Simulated results for all models achieved overall R2 of minimum 0.990 with MAE and MAPE of not higher than 7%. Figure 21 illustrates the statistical parameters of ANN and LSSVM for further comparison.

Table 8 Statistical results for prediction of shear stress
Full size table
Table 9 Statistical results for prediction of filtration volume
Full size table
Fig. 21
figure 21

Comparison of statistical parameters

Full size image

Based on Table 8, the regression coefficient of ANN and LSSVM in the prediction of shear stress is 0.9937 and 0.9941, whereas the RMSE is 1.7235 lbf/ft2 and 1.6003 lbf/ft2, respectively. LSSVM model slightly outperforms ANN in predicting shear stress in terms of a higher R2 and lower RMSE and MAPE. The R2 of LSSVM is 0.04% higher than ANN, whereas the RMSE is 7.1% lower than ANN. According to Table 9, both models achieved an ideal prediction of filtration loss with R2 of higher than 0.999. The comparison showed that the R2 of ANN in the prediction of filtration volume is 0.05% higher than LSSVM, and RMSE is 33.7% lower than LSSVM. Hence, the prediction of ANN is more precise than LSSVM in predicting filtration loss.

Based on the analysis, both machine learning models are equally competent and capable of predicting the required parameters with high precision and accuracy. The accuracy of both machine learning models in predicting the filtration volume is generally higher than shear stress as indicated by all the statistics and the relative error distribution plot. One of the possible reasons could be due to a larger quantity of datasets available for the training.

Validation of the predicted outputs

The predicted output from the machine learning model with the best performance is plotted along with the corresponding experimental values to validate the trend of the predicted output. For the prediction of shear stress, predicted values from LSSVM is utilised in Fig. 22 as LSSVM performs better than the ANN. Figure 21 shows the rheo-grams of the SiO2 nanoparticle WBM at 78°F and 140°F at varying nanoparticles concentration. Shear-thinning behaviour can be observed from both experimental and predicted trendlines at all concentration of SiO2. The magnitude or gradient of shear-thinning is more noticeable and significant at a higher SiO2 nanoparticle concentration. This behaviour is favourable for a drilling fluid as low viscosity is preferred at a high shear rate to circulate the drilling fluid and cuttings. High viscosity at a low shear rate may ease the suspension of the drill cuttings during a drilling break.

Fig. 22
figure 22

Predicted and experimental rheo-gram. a 78 °F (b) 140 °F

Full size image

The predicted filtration volume at 77 °F and 199 °F with a concentration ranging from 0 to 7.5 wt% is shown in Fig. 23. The predicted output from ANN is utilised in the plot as it has the best performance. The trend of both predicted and experimental output increases logarithmically with time, and filtration loss decreases with the increasing concentration of nanoparticles. The reduction in filtration loss can be justified by the nano-sized particles that can clog the pore throats on the filter paper compared to conventional drilling fluid particles.

Fig. 23
figure 23

Predicted and experimental filtration loss. a 77 °F (b) 199 °F

Full size image

Conclusions

Prediction of shear stress and filtration loss of SiO2 nanoparticles water-based drilling fluid are accomplished by two machine learning-based approaches, i.e. ANN and LSSVM. The developed models demonstrate a well generalisation and a low tendency in overfitting. The predicted results for both models achieved R2 of higher than 0.99 and both MAE and MAPE not exceeding 7%. The RMSE for the predicted shear stress and filtration volume is lower than 1.8 lbf/ft2, and 0.2 mL, respectively. The following conclusions are deduced based on the predictive performance of developed ML models.

  1. 1.

    The assuring performances proved that both ANN and LSSVM are capable of predicting the output based on the precision of provided inputs.

  2. 2.

    It is found that LSSVM outperforms the ANN in the prediction of shear stress, whereas for the prediction of filtration volume, ANN performs better than the another. There is no definite conclusion of which machine learning approach is more superior in this research.

  3. 3.

    A shear-thinning behaviour is observed in the rheo-gram and a noticeable logarithmic increment of filtration loss with time.

  4. 4.

    The developed machine learning models are comprehensive and efficient in predicting the shear stress and filtration volume of a SiO2 nanoparticles water-based drilling fluid.