Introduction

Due to the ultra-low porosity and permeability of low-permeability carbonate reservoirs, economic development cannot be achieved by conventional production methods, and large-scale fracturing treatments are shown to provide economic production (Zillur et al. 2002; Jeon et al. 2016; Qiao et al. 2022). For hydraulic fracture modeling, many simulation studies approximated the fractures as simple double-wing plane-like fractures and used local mesh refinement to simulate the stimulated volume after hydraulic fracturing (Zhao et al. 2022). In real applications, the fracture networks formed after large-scale fracturing of horizontal wells are rather complex, these simplified and approximate methods are insufficient to simulate production behavior from the real fracture networks after hydraulic fracturing.

The geological, geomechanical, and development factors that affect the geometry of the hydraulic fracture network include the value and orientation of in-situ stress, the properties of natural fractures such as distributions and densities, fracturing design and implementation, as well as pumping parameters (Cipolla et al. 2011a and 2011b; Sun et al. 2015; Vishkai and Gates, 2019; Suboyin et al. 2020). The integrated geological engineering technology, which is based on the coupled simulation of fracture propagation and reservoir fluid flow, has been shown to be an effective tool that can comprehensively consider the influence of above factors (Olsen 2008; Cheng et al. 2012; Weng et al. 2014; Wu and Olson, 2015; Wu et al. 2015; Zhang et al. 2020; Fu et al. 2020).

At present, many papers have present field applications using the integrated geologic and engineering approach for hydraulic fracturing modeling and production forecast in unconventional oil and gas reservoirs, but mainly for tight sandstone and shale formations (Wu et al. 2015; Saberhosseini et al. 2017; Vishkai and Gates 2019; Wang et al. 2019; Yong et al. 2021; Lu et al. 2022a and 2022b). In this paper, this method is applied to the hydraulic fracturing design for a carbonate reservoir in Middle East. Using the integrated geological engineering technology, an integrated workflow that couples fracturing modeling and reservoir simulation has been employed, from which the rock mechanics model and reservoir model have been calibrated via history matching against production data and pumping pressure history. Based on the calibrated models, physical sweet spots and engineering sweet spots are obtained, which represent the productivity of oil wells and the difficulty of hydraulic fracturing, respectively. As last, we show the hydraulic fracturing design and results for a horizontal well based on the productivity charts obtained via sweet spot mapping.

Background

The target reservoir is a typical low permeability and porosity carbonate reservoir in Iraq, and its reserves account for 24.9% of the whole oilfield. The vertical pay zone is divided into B1, B2, B3, and T layers, The B1 and B2 layers are mainly biochip pores, and the average pore throat radius is about 0.1 μm, which is microporous media. The average porosity of B1 and B2 layers is 15.5–17.6%, and the permeability is lower than 0.1mD. The porosity and permeability of B3 and T layers are slightly higher, but the proportion of reserves is low (< 30%).

There are three hydraulically fractured wells (H5S, N55, and N52) in the target reservoir, among which the H5S well has the best performance after fracturing and the N52 well has the worst performance, as shown in Fig. 1. Fig. 1 Daily oil production of three hydraulically fractured wells 1.

Fig. 1
figure 1

Daily oil production of three hydraulically fractured wells 1

Full size image

The production of fractured wells is not only affected by fracturing scale, well type, horizontal length, numbers of fracturing stages, but also affected by reservoir petrophysical parameters and rock mechanics parameters. Therefore, it is important to analyze the main controlling factors of productivity to determine the optimum well location and fracturing scale.

An integrated workflow of hydraulic fracturing modeling

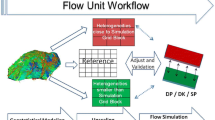
The integrated workflow consists of the following steps as shown in Fig. 2:

  1. (1)

    Set up one-dimensional and three-dimensional rock mechanics model using well-log data.

  2. (2)

    Fit and adjust the rock mechanics model by comparing against experimental data and pumping pressure history of fractured wells.

  3. (3)

    Determine the engineering sweet spots based on rock mechanic model and parameters; physical sweet spots are determined based on reservoir petrophysical data.

  4. (4)

    Implement the fracturing scheme for different sweet spot combinations and obtain the optimum fracturing parameters based on post-fracturing productivity and reservoir pressure distribution, as shown in Fig. 2. Fig. 2 the Integrated Workflow of hydraulic fracturing and reservoir modeling2

Fig. 2
figure 2

the Integrated Workflow of hydraulic fracturing and reservoir modeling2

Full size image

The detailed implementation of the integrated workflow described in Fig. 2 above consists of geological analysis, rock mechanics interpretation, fracturing modeling, and reservoir evaluation. Figure 3 below demonstrates the software used for these analyzing and modeling processes, which includes Techlog (for well logging analysis), Petrel (for geological modeling), Mangrove (Kinetix), and Intersect (for fracturing modeling and reservoir simulation).

Fig. 3
figure 3

Complete implementation diagram of the integrated process of geology, engineering, and reservoir simulation 3

Full size image

Geomechanics

As provided in Table 1 below, the data used for geomechanical modeling include P-wave time difference and natural gamma ray log curves of a total of 363 wells, laboratory experimental parameters (e.g. static and dynamic Young's modulus) of the one well (well V36), and fracturing parameters of four hydraulically fractured wells, which can be used as the data set for rock mechanics model.

Table 1 Data sources of reservoir geomechanical model construction1
Full size table

Shear wave prediction

There is a total of eight wells that have S-wave data that meet the requirements of rock mechanics calculation, which is insufficient for the rock mechanics model in the area. At present, most shear wave prediction methods use empirical formula. Which does not consider the characteristics of the actual reservoir, nor does it consider the influence of different formation properties on the prediction of shear wave time difference. Therefore, rock mechanics calculation based on shear wave prediction obtained by empirical method tends to lead to unreasonable subsequent parameters (Al-Ruwaili and Chardac, 2003). This study fully considers the geological characteristics, takes the wells with S-wave as the template, and predicts the S-wave data of other wells through a multi-factor neural network. The procedure is as follows:

  1. (1)

    The influencing factor set

    Three indexes, including compressional wave, gamma ray, and shale content, are used as the influencing factor set for a single well.

  2. (2)

    Multi-well training

    Based on all the wells with the complete data set of shear wave, compressional wave, gamma ray, and shale content, data training is conducted to establish the nonlinear relationship between compressional wave, gamma ray, shale content, and shear wave to prepare for the next fitting test.

  3. (3)

    Fitting existing well S-wave data

    To establish the relationship between multiple indicators and S-wave time difference, the existing S-wave data of the wells are fitted, and the parameters of the constructed neural network are adjusted to obtain the S-wave data predicted by the model match the actual S-wave data. The resulting neural network model is used to predict the S-wave data of other wells.

  4. (4)

    Prediction of shear wave data of unknown Wells

The fitted neural network model is used to predict shear wave data of other wells. Taking compressional wave, gamma ray, and shale content of other wells as input data, the S-wave data of this well is obtained through the calculation of the existing neural network model.

See Fig. 4 for the schematic diagram of the above process. Detailed calculation results are shown in Fig. 5.

Fig. 4
figure 4

Shear wave prediction based on a neural network model

Full size image
Fig. 5
figure 5

Shear wave prediction calculation results based on a neural network model

Full size image

The comparison between the measured and predicted S-wave data from eight wells is shown in Fig. 6. It can be observed that the predicted results can take the variation characteristics of S-wave data are fully captured.

Fig. 6
figure 6

Comparison between measured and predicted shear wave data

Full size image

Rock mechanics parameters

Young's modulus and Poisson's ratio

In this study, dynamic Young's modulus and dynamic Poisson's ratio are obtained using the following correlation based on P-wave and S-wave data and are calibrated with measured data, as shown in Fig. 7.

$$E_{{\text{d}}} = 929 \cdot 10^{5} \cdot \frac{\rho }{{\Delta t_{{\text{s}}}^{2} }} \cdot \frac{{3\Delta t_{{\text{s}}}^{2} - 4\Delta t_{{\text{p}}}^{2} }}{{\Delta t_{{\text{s}}}^{2} - \Delta t_{{\text{p}}}^{2} }}$$
(1)
$$\mu_{{\text{d}}} = \frac{{0.5\Delta t_{s}^{2} - \Delta t_{p}^{2} }}{{\Delta t_{s}^{2} - \Delta t_{p}^{2} }}$$
(2)

where

Fig. 7
figure 7

Comparison between calculated and measured dynamic Poisson's ratio

Full size image

\(E_{{\text{d}}}\)– Dynamic Young's modulus, GPa;

\(\mu_{{\text{d}}}\)– Dynamic Poisson's ratio, decimal.

The acoustic logging curve is used to calculate the young's modulus and Poisson's ratio, which are dynamic values. They need to be converted to static ones for simulation after combing with the experimental data via regression. In Fig. 8, static data are from triaxial stress test results, and dynamic data are from acoustic characteristics test results.

Fig. 8
figure 8

Calculation results of Dynamic Young's modulus and Poisson's ratio in well V36

Full size image

According to the static and dynamic conversion relationship between Young's modulus and Poisson's ratio in Fig. 8, the parameters measured in the front acoustic logging are converted to obtain the static parameters, which are compared with the triaxial stress static test results (taking well V36 as an example, as shown in Fig. 9). The errors of the two parameters are small and meet the requirements of rock mechanics parameter calculation.

  • Other parameters

Fig. 9
figure 9

Comparison of calculation results of static Young's modulus and Poisson's ratio with experimental static data in well V36

Full size image

Based on the above calculation of rock mechanical parameters, the maximum horizontal principal stress, minimum horizontal principal stress, fracture pressure, vertical stress, fracture toughness, shear modulus, confining pressure, pore pressure gradient, vertical stress gradient, and other indicators are also calculated. The corresponding calculation model is as follows:

Maximum horizontal principal stress (the calculation results are shown in SHMax in Fig. 10):

$$\sigma_{{\text{H}}} = \frac{{\mu_{{\text{s}}} }}{{1 - \mu_{{\text{s}}} }}\left( {\sigma_{{\text{v}}} - \alpha P_{{\text{p}}} } \right) + \beta_{2} \left( {\sigma_{{\text{v}}} - \alpha P_{{\text{p}}} } \right) + \alpha P_{{\text{p}}}$$
(3)
Fig. 10
figure 10

One-dimensional rock mechanics parameters of well H5S

Full size image

Minimum horizontal principal stress(The calculation results are shown in SHMin in Fig. 10):

$$\sigma_{{\text{h}}} = \frac{{\mu_{{\text{s}}} }}{{1 - \mu_{{\text{s}}} }}\left( {\sigma_{{\text{v}}} - \alpha P_{{\text{p}}} } \right) + \beta_{1} \left( {\sigma_{{\text{v}}} - \alpha P_{{\text{p}}} } \right) + \alpha P_{{\text{p}}}$$
(4)

Rupture pressure (The calculation results are shown in Pfrac in Fig. 10):

$$P_{{\text{f}}} = 3\sigma_{{\text{h}}} - \sigma_{{\text{H}}} - \alpha P_{{\text{p}}} + S_{{\text{z}}}$$
(5)

Tensile strength (The calculation results are shown in TSTR in Fig. 11):5

$$S_{t} = S_{c} /c$$
(6)
Fig. 11
figure 11

One-dimensional rock mechanics parameters of well N52

Full size image

The calculation formula of \(S_{{\text{c}}}\):6

$$S_{{\text{c}}} = \left( {0.0045E_{{\text{D}}} \left( {1 - V_{{{\text{sh}}}} } \right) + 0.008E_{{\text{D}}} V_{{{\text{sh}}}} } \right) \times 1000d$$
(7)

Vertical stress (The calculation results are shown in SHV in Fig. 11):

$$\sigma_{{\text{z}}} = 10^{6} \int_{0}^{H} {\rho_{{\text{r}}} } (h)g{\text{d}}h$$
(8)

Fracture toughness (The calculation results are shown in Pt in Fig. 11):

$$P_{{{\text{frac }}_{ - } T}} = 0.217P_{{\text{c}}} + 0.0059S_{{\text{t}}}^{3} + 0.0923S_{{\text{t}}}^{2} + 0.517S_{{\text{t}}} - 0.3322$$
(9)

Confining pressure (The calculation results are shown in Pc in Fig. 11):

$$P_{{\text{c}}} = \frac{{\mu_{{\text{S}}} }}{{\left( {1 - \mu_{{\text{S}}} } \right)}}\left( {\sigma_{{\text{z}}} - \alpha P_{{\text{p}}} } \right) + \alpha P_{{\text{p}}}$$
(10)

Shear modulus (The calculation results are shown in YMOD in Fig. 11):

$$G = \frac{{E_{{\text{d}}} }}{{2\left( {1 + \mu_{{\text{d}}} } \right)}}$$
(11)

where,

\(\sigma_{{\text{H}}}\)– Maximum horizontal stress, MPa;

\(\sigma_{{\text{h}}}\)– Minimum horizontal stress, MPa;

\(\sigma_{{\text{v}}}\)– Vertical principal stress, MPa;

\(P_{{\text{p}}}\)– Reservoir pore pressure, MPa;

\(\alpha\)– Biot elastic coefficient, decimal, theoretical value is "1-porosity", but needs to be adjusted in the fitting;

\(\beta_{1}\)、\(\beta_{2}\)– horizontal tectonic stress coefficient, decimal.

\(P_{{\text{f}}}\)– Rupture pressure, MPa;

\(P_{{\text{p}}}\)– Reservoir pore pressure, MPa;

\(S_{{\text{t}}}\)– Tensile strength, MPa;

\(c\)– The empirical coefficient of compressive strength and tensile strength of rock, the value is generally between 2–20;

\(S_{{\text{c}}}\)– Compressive strength, MPa;

\(V_{{{\text{sh}}}}\)– Mud content, decimal;

\(d\)– Correction coefficient, 1.2;

\(\sigma_{{\text{z}}}\)– Vertical stress, MPa;

\(\rho_{{\text{r}}} (h)\)– Overburden density with depth, kg/m3;

\(h\)– Formation depth, m;

\(g\)– Acceleration of gravity, m/s2;

\(P_{{{\text{frac }}_{ - } T}}\)– Fracture toughness, MPa, here refers to type I fracture;

\(G\)– Shear modulus, GPa;

1D and 3d rock mechanics models

Based on the above geomechanical model and typical mechanical parameter calculation model, one-dimensional rock mechanical parameters of more than 300 wells are predicted in combination with the location of the drilling platform. For the target area, two existing fractured Wells N52 and H5S are taken as examples, as shown in Figs. 11 and  12.

Fig. 12
figure 12

Longitudinal discretization of Poisson's ratio

Full size image

Based on the one-dimensional rock mechanics model, the arithmetical average method is used to discretize the predicted rock mechanics parameters longitudinally. Young's modulus, Poisson's ratio, and horizontal principal stress are taken as examples, as shown in Figs. 12, 13, and 14.

Fig. 13
figure 13

Longitudinal discretization of Young's modulus

Full size image
Fig. 14
figure 14

Longitudinal discretization of minimum horizontal principal stress

Full size image

Furthermore, 3D rock mechanics model is obtained through plane prediction. Due to the uncertainties in the geological model, geomechanical model, and fracture propagation simulation model, further calibration and correction of input parameters are needed to ensure the accuracy of simulation results. The comprehensive calibration flow chart is shown in Fig. 15. The correction results are shown in Figs. 16, 17, and 18.

Fig. 15
figure 15

Comprehensive flow chart of the model calibration

Full size image
Fig. 16
figure 16

Poisson’s ratio

Full size image
Fig. 17
figure 17

Young's modulus

Full size image
Fig. 18
figure 18

Minimum horizontal principal stress

Full size image

Sweet spot mapping

  1. (1)

    Engineering sweet spots

    Considering the characteristics of reservoir rocks in interest, we focus on the brittleness index, horizontal principal stress ad fracture toughness, which is used to set up the fracturing index, namely engineering sweet spots, representing the level of easiness of fracturing. The index is further divided into three levels: I, II, and III, of which level I reservoir quality represents the easiest cases of fracturing. The classification of engineering sweet spots is summarized in Table 2.

  2. (2)

    Physical sweet spots

Table 2 Classification summary of single index of engineering sweet spots2
Full size table

In this study, petrophysical properties such as permeability, porosity, oil saturation, and effective thickness are considered to characterize the capability of post-fracturing oil production. Like the engineering sweet spots, the physical sweet spot index is divided into three levels, of which level I reservoir is the best, representing the highest oil production capability. The classification of engineering sweet spots is summarized in Table 3.

Table 3 Classification summary of single index of physical sweet spots3
Full size table

Based on the classification of engineering and physical sweet spots indexes, the sweet spot maps are obtained respectively, as shown in Fig. 19 and Fig. 20. There are engineering sweet spots in the middle and southeast of B1 and B2 layers, but there are few engineering sweet spots in the middle of B3 layers, and there are no engineering sweet spots in T layers. B1 and B2 layers are the main layers for hydraulic fracturing deployment, given the physical sweet spot distribution. In the middle of B2 layer, physical sweet spots are developed, while in B1 layer, physical sweet spots of B3 and T are the least developed. Considering the relatively high permeability in B3 and T layers, hydraulic fracturing is not recommended in B3 and T layers.

Fig. 19
figure 19

Distribution of engineering sweet spots

Full size image
Fig. 20
figure 20

Distribution of physical sweet spots

Full size image

Productivity evaluation when fracturing under different sweet spot combinations

This section takes B2 layer as example and provides the post-fracturing productivity forecast for the wells under different hydraulic fracturing parameters. Based on the combination of sweet spots, B2 layer can be divided into the following sweet spot combinations as shown in Table 4. The sweet spots of Physical 1 + Engineering 1, Physical 2 + Engineering 1 and Physical 3 + Engineering 1 are the main ones, which account for 42.74% of reserves, and thus are studied in detail here.

Table 4 Proportion of sweet spot combination in B2 layer
Full size table

To evaluate the single well production capability under different sweet spot combinations, the volume of the proppant and fracturing fluid, number of fracturing stages, and horizontal section length are considered as control variables, based on which six different fracturing schemes are proposed. We further discuss the effects of changing these variables on horizontal good productivity.

Three combinations of Physical 1 + Engineering 1, Physical 2 + Engineering 1, and Physical 3 + Engineering 1 are analyzed. The fracture half-length obtained by fracturing simulation is mainly between 75-135 m, and the conductivity is mainly between 1200-2100mD.m. In the fracturing process of horizontal wells, fracture distribution under different proppant amount is illustrated in Fig. 21. Compared to using 50000 kg proppant, when the amount of proppant is 150000 kg, fracture length is higher and fracture volume is larger, which leads to higher productivity.

Fig. 21
figure 21

Fracture under different proppant amount

Full size image

For the combination of Physical 1 + Engineering 1, the productivity of each scheme is shown in Fig. 22 below.

Fig. 22
figure 22

Productivity changes under various factors

Full size image

As shown in Fig. 22, when the injected proppant ranges from 50,000  to 150,000 kg, the corresponding horizontal well productivity ranges from 1000 to 1600 bbl/d. When it comes to less than 900,00 kg, the amount of proppant injected has a strong effect on single well productivity. When the production per well reaches 1500 bbl/d at 90,000 kg of proppant, the rate increase with proppant amount becomes less significant. The effect of fracturing fluid volume on single well productivity is smaller, as the fracturing fluid is between 400 m3 to 900 m3, the corresponding horizontal well productivity is 1400 to 1550 bbl/d. When fracturing fluid volume is less than 500/m3, the effect of increasing fracturing fluid volume on single well productivity becomes more significant. When the productivity of a single well is 1500 bbl/d, the effect of increasing fracturing fluid quality on single well productivity is weakened. The number of fracture stages and horizontal well sections have a significant effect on single well productivity when the production is observed to range from 1050 to 1600 bbl/d at 6 to 16 fracture stages. When the number of stages reaches 14, the increase in productivity is more obvious with the increasing number of stages, and then the effect becomes smaller. The horizontal section length has the greatest impact on productivity. When the horizontal section length is increased from 1000 to 2000 m, the productivity increases from 1500 to 2500 bbl/d. When the horizontal section length increases from 1000 to 1600 m, the effect is the most significant, and then the impact becomes less pronounced.

Based on the discussion above, for the sweet spot combination of Physical 1 + Engineering 1, proppant and horizontal length have a greater impact on productivity, while fluid volume has a smaller impact. The productivity chart of the sweet spot combination of Physical 1 + Engineering 1 is obtained, as shown in Fig. 23.

Fig. 23
figure 23

Production capacity chart under various factors combination

Full size image

Through a similar analysis of Physical 1 + Engineering 1, the productivity charts of the combination of two sweet spots of Physical 2 + Engineering 1 and Physical 3 + Engineering 1 are obtained, as shown in Figs. 24 and Fig. 25.

Fig. 24
figure 24

Physical 2 + Engineering 1 capacity chart

Full size image
Fig. 25
figure 25

Production capacity chart under various influencing factors

Full size image

By changing the four factors affecting the productivity of horizontal wells, the productivity range of each sweet spots combination horizontal well is obtained as follows:

Discussion

Through the productivity analysis of different sweet spot combinations in Sect. 4, the following understandings are obtained:

  1. (1)

    Based on the analysis of physical properties and distribution of engineering sweet spots, it can be observed that B1 and B2 layers have more engineering sweet spots in the middle and southeast, B3 layers have less engineering sweet spots in the middle, and T layers have no engineering sweet spots. B1 and B2 layers are the main layers for hydraulic fracturing. In the middle of B2 layer, physical sweet spots are developed. B2 layer is the main layer contributing to oil production. Considering that B3 and T layers have good permeability, production and development could be carried out without fracturing.

  2. (2)

    The sweet spot combination of Physical 3 + Engineering 1 yields the lowest production, ranging from 180 to 430 bbl/d. Physical 2 + Engineering 1 sweet spot combination yields high productivity, ranging from 500 to 1900 bbl/d; Physical 1 + Engineering 1 sweet spot combination leads to the highest capacity, ranging from 1000 bbl/d to 2500 bbl/d. For the sweet combination of physical 2 + Engineering 1 and physical 1 + Engineering 1, the productivity crossover part shown in Fig. 26 is mainly realized by increasing the length of horizontal section.

  3. (3)

    Under different sweet spot combinations, the productivity of sweet spots with different physical properties intersects with each other. The effect of level II and III physical sweet spots can be improved by taking the advantages of engineering sweet spots. Therefore, the sweet spot combination areas of Physical 1 + Engineering 1 and Physical 2 + Engineering 1 should be considered as the main areas in the development process, while the sweet spot combination areas of Physical 3 + Engineering 1 should be ignored, and the model could further established to optimize the development strategy by increasing the horizontal section length and proppant amount injected.

Fig. 26
figure 26

Production range of different sweet spot combinations

Full size image

Application example

Here we show a preliminary application example, which is performed under the guidance of our observation above. Well H24S was put into production in December 2020, which is located in the combination area of physical sweet spot 1 + engineering sweet spot 1. It is perforated in B2 layer with a horizontal section length of 1000 m and 12 fracturing stages with an average fracturing fluid consumption of 500 m3 per stage. The initial fracturing production reaches above 2000 bbl/d and the production data show a relatively extensive stabilized period of three months before declining, which suggests a satisfactory fracturing outcome as shown in Fig. 27. It can also be observed in Fig. 27 that the production of well H24S is consistent with the productivity chart.

Fig. 27
figure 27

Daily oil distribution of well H24S

Full size image

Conclusions

This paper presents a field case study of hydraulic fracturing design of a low-permeability carbonate reservoir. Using the integrated geological and engineering modeling approach, the productivity charts based on physical and engineering sweet spots are constructed, and the following conclusions and understandings are obtained:

  1. (1)

    The amount of proppant has a significant influence on fracture length and conductivity; thus the optimal proppant amount is the primary consideration in fracturing design.

  2. (2)

    The main controlling factors of the production capacity of wells with both good engineering sweet spot and good physical sweet spot are proppant amount and horizontal length. For the wells with good engineering sweet spot and middle physical sweet spot, the main controlling factors of the production capacity are proppant amount and horizontal well length; For the wells with good engineering sweet spot and poor physical properties, the main controlling factors of productivity are number of fracturing stages and horizontal length.

  3. (3)

    The productivity of wells with good engineering sweet spot and middle physical sweet spot can improved through large fracturing scale. The hydraulic fracturing for wells with good engineering sweet spot and poor physical sweet spot could be excluded future fracture design due to low production capacity.

  4. (4)

    This study focuses on the effect of combination of physical and engineering sweet spots on the production capacity in the sweet spot mapping process. The influence of geomechanics models/ parameters variations on fractures and production will be further studied in our future work.