Feasibility study of underbalanced drilling using geomechanical parameters and finite element method

Abstract

Wellbore instability causes main concerns in the oil and gas industry due to personnel safety and overall expenditure. Several signs such as wellbore spalling, the rate of penetration reduction, pipes sticking, well unnatural wash out, wellbore collapsing, induce fracture could indicate wellbore instability during drilling. A balance between stress concentration near the wellbore and rock strength is the primary condition for a wellbore stability during drilling. Thus, instability due to the failure of wellbore rocks occurs when the intensity of the effective stress exceeds rock strength. In underbalanced drilling (UBD), the wellbore is considered unstable since no pressure or maybe not enough pressure is applied on the well from the drilling fluid, and the pore pressure is considered undesirable stress on the wellbore, so the difference between these two pressures is applied on the wellbore. Consequently, the wellbore instability issue in the UBD approach is of great importance. UBD is mainly used to reduce the damage to geological formation and the risk of drilling fluid loss while increasing the drilling rate. This study has investigated the stability of a well in Iranian Oilfield using FLAC software considering yielded regions (plastic) for different mud weights. The investigation and analysis of the FLAC output plots, especially the plasticity plot, concluded that the ideal and optimal pressure for applying UBD conditions while also ensuring wellbore stability ranges 15.2–16.8 MPa.

Introduction

Most near-wellbore formation damages during drilling operations are due to the infiltration of external fluids and solids to the area around the wellbore during overbalanced drilling because the drilling fluid’s pressure exceeds that of the formation (Tanha et al. 2022; Zargar et al. 2020). UBD mainly refers to a drilling operation condition under which the drilling fluid pressure is lower than the formation pressure, and as a result, infiltration and loss of drilling fluids and solids into the formation are stopped, and damages are minimized (Chakroborty et al. 2018; Guo et al. 2003). The results are reducing the cleaning time of the well after drilling, increasing production from the wells, and the ultimate recovery (Guo and Ghalambor 2004). This drilling approach is used worldwide in horizontal and vertical wells to reduce mud invasion and common problems involving mud loss and mechanical pipe sticking (Guo and Ghalambor 2006; Shahbazi et al. 2020). Although UBD is a solution for reducing formation damage, incorrect designing may lead to formation damage greater than the overbalanced drilling approach (Guo et al. 2008; Guo and Shi 2007). UBD is mainly used in natural fracture formations, locally-depleted, and heavy oil reservoirs to increase production. One of the most severe problems during UBD is wellbore instability and collapse further down into the well (Guo et al. 2014; Zhang et al. 2012). Fluid hydrostatic pressure inside well is less in UBD than in overbalanced drilling. This may cause wellbore instability resulted from borehole failure (Zhang et al. 2018). Wellbore instability may cause issues such as tight holes, pipes sticking, mud loss, and Poor hole-cleaning (Bagheri et al. 2021; Zhang et al. 2016).

Fluid hydrostatic pressure inside the well is lower in UBD in comparison with overbalanced drilling, which may cause wellbore instability resulting from borehole failure. Less pressure may increase the tendency of the wellbore to tighten in some formations. Big pieces of shale observed in UBD are not the result of drilling bit at the bottom of the well but from the holes on the wellbore or the wellbore becoming muddy (Yumei et al. 2018). When drilling shale layers using the UBD approach, falling shale pieces and severe wellbore instability may be observed. This risk is specifically higher when the characteristics and pressure of the reservoir are weak. This type of well instability may happen when the drilled formation has significant shales sensitive to water. Change in water volume of the shale through water surface absorption causes extra stress on the rocks around the wellbore, making it unstable. If the bottom of the well abruptly becomes muddy, it may cause mechanical pipe sticking. UBD may positively influence wellbore stability. For example, overbalanced drilling of the shaly formations containing active clay frequently causes problems due to relative water absorption, swelling, and pore pressure effects resulting from drilling mud filtrated absorption to formation. Wellbore instability may be aggravated in some cases. For example, when the applied bottom-hole pressure is low, it may increase the shear stresses applied to the wellbore and thus increase the risk of shear failure. High pressure gradient in the influx from around the wellbore may cause stress failure. The optimal bottom-hole pressure has to be high enough to maintain underbalanced conditions while preventing formation collapse and formation damage. Therefore, geomechanical modeling has to be used to predict the optimal pressure spectrum of the bottom of the well to prevent formation failure (Larki et al. 2022).

The effects of overburden pressure, horizontal in-situ stresses, drilling mud pressure, pore pressure, and temperature on stress distribution of bottom-hole rock are examined by Zhang et al. (2018) that using a fully coupled simulation model (Zhang et al. 2018). The most prominent source of wellbore instability, according to Aadnoy and Ong (2003), is inappropriate mud weight (MW) and well path. Based on the stress distribution model, failure criteria, and the breakout width model, Ma et al. (2015) suggested a semi-analytic model of wellbore stability analysis. This semi-analytic model uses the Mogi–Coulomb criterion, a new true-triaxial failure criterion, to determine shear failure. McLean and Addis (1990b) examine how two generally stated failure criteria affect mud weight choices. The failure criteria chosen have a major impact on the computed ‘safe’ mud weights. By analyzing data using quantitative risk assessment, Gholami et al. (2015) were able to analyze the effect of uncertainty on the estimation of safe MWW using various failure criteria. In some situations, Salehi et al. (2010) found that using a good geomechanical model description that matches field parameters and rock failure criteria can lead to a good forecast for avoiding wellbore stability difficulties and selecting the best mud weight window. During underbalanced drilling conditions, Yumei et al. (2018) investigated the fluctuation of pore pressure near the wellbore wall with seepage time and the influence of time delay on wellbore stability. The maximum displacement and maximum plastic deformation around the borehole wall as a function of bottom pressure were investigated. Wellbore instability, borehole failure, stresses around the wellbore when alternative material constitutive equations are used (Gaede et al. 2012), and wellbore strengthening are the principal topics of most FEM investigations (Feng and Gray 2016a; Grandi et al. 2002). The effects of other parameters, such as thermal and chemical properties (Wang et al. 2017; Zhou and Ghassemi 2009) as well as investigating borehole stability in steady-state and transient situations under various drilling fluid pressure, are also showing FEM contribution to increasing our knowledge in this subject. Hodge et al. describe a fully coupled poroelastic model for wellbore stability analysis, focusing on fluid flow induced stress variations around the wellbore (Hodge et al. 2006). The model can compute both geomechanical and hydraulic variables simultaneously using finite element methods. Hu et al. provided a dynamic response and strength failure study of bottomhole under UBD conditions. He et al. (2020) demonstrated that it is vital to study stress distribution around the wellbore for wellbore safety during the analyses of the drilling techniques. A model of pore pressure distribution under anisotropic seepage of horizontal wells was created utilizing conformal transformation to handle seepage and thermal effects during UBD.

Fluid seepage due to negative pressure causes additional stress during UBD; earlier researchers focused primarily on isotropic seepage, such as He et al. (2015, 2014), who studied the wellbore stability of UBD using a pore pressure distribution equation provided by Qiu et al. (2008) under isotropic seepage. The well response during drilling suggested that the FEM predictions were substantially more accurate than the linear-elastic analysis, according to McLean and Addis (1990a). In geotechnical research, the finite element method (FEM) is widely used as an effective tool for assessing stress and strain status. The accuracy and precision of FEM findings are highly influenced by the beginning and boundary conditions, element type, and meshing system (Ravaji et al. 2018). Three prior wellbore stability investigations employing the breakout-width-failure model were presented by Abdelghany et al. (2021) after several attempts in previously drilled wells in overbalanced conditions that resulted in borehole instability and/or formation damage; such study has helped to achieve exceptional outcomes during underbalanced drilling. A wellbore-stability study was done by Qiu et al. (2008) to determine the possibility of employing UBD technology to drill a horizontal well in a substantially depleted reservoir. To obtain induced stresses around the wellbore, Akbarpour and Abdideh (2020) employed a numerical approach and Phase 2 software. The modulus of elasticity, Poisson’s ratio, cohesive bond, friction angle, overburden stress amount, minimum and maximum horizontal stresses along the well depth, and their variations have been investigated and their variations have been shown, and then the wellbore stabilities have been simulated. As the stress conditions change, the formation’s poroelastic response deviates from the elastic module, especially in the vicinity of the wellbore. This might eventually lead to the redistribution of stress planes and pore networks, validating the fact that near-wellbore deformation is time-dependent (Gao and Gray 2020). Production loss, circulation loss, and in extreme cases the loss of the entire well might occur due to stalled wellbore failure in UBD (Hodge et al. 2006). Han et al. (2021) demonstrated a poro-visco-elastic Finite Element Method simulator for quantifying time-dependent shale zone borehole deformation. Time-dependent borehole deformation is dominated by the rock’s viscoelastic characteristics (Han et al. 2021). In this study, we aim to propose a fully coupled poroelastic model for wellbore stability analysis, focusing on flow caused by stress alteration around the wellbore. The model will simultaneously compute the geomechanical equations through the finite element approach.

The viability of UBD to maintain wellbore stability was analyzed in this study. The FEM approach and FLAC software were utilized to determine the feasibility of the application of UBD. This approach's main advantage is determining the necessary weight of drilling mud for the entire field by analyzing a single well. This study has investigated wellbore instability factors in one of the wells of an Iranian Oilfield, determines the yield points using FEM in the characteristics of poroelastic environments, and presents the necessary approaches to prevent this problem.

Methodology

The Numerical geomechanical model produced from the in-situ stresses, pore pressures and the mechanical characteristics of rock for a part of specific stratigraphy in an oilfield. Here, are the stages of constructing a geomechanical model:

• Preparing a model based on geomechanical and geological information

• Analyzing wellbore stability for the prepared model

• Using geomechanical information for maximum selection with the optimal drilling mud weight from numerical analysis of wellbore stability.

Then, the parameters used to construct the geomechanical model have been calculated as shown in Fig. 1.

Fig. 1

A schematic view of the steps towards constructing a geomechanical model

Geological setting

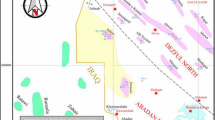
One of the wells of an oilfield in the southwest of Iran was targeted in this study. It is an asymmetric anticline structure facing northwest-southeast, with a length and width of 36 and 7 km, respectively. The noticeably high-water salinity and the limited flow of the reservoir imply that the region between the two thrust faults is confined. The well has been drilled from 2700 to 2850 m depth. The lithology of the well has been determined using a photoelectric log and density log. According to Fig. 2, it mostly consists of carbonated rocks (dolomite and lime), sandstone, and shale areas. In order to determine the lithology more accurately, the corrected gamma diagram of the well has been drawn in Fig. 3. Then, areas exceeding API 50, which we considered “cut-off” consisting of shale, were specified. As shown in Fig. 3, from 2700 to 2850 m consist of a negligible shale percentage (Larki et al. 2021).

Fig. 2

Formation lithology

Fig. 3

CGR log diagram

Elastic coefficients of the geological formation

Elastic coefficients are achieved using acoustic and density logs. The dynamic elastic coefficients expressing the characteristics of rock are Young’s modulus (E_dyn), Bulk modulus (K_dyn), Shear modulus (G_dyn), and Poisson’s ratio $(\nu_{{{\text{dyn}}}} )$ which is estimated using pressure and shear acoustic log with the following equations(Zoback et al. 2003):

$$E_{{{\text{dyn}}}} = \frac{{\rho_{{\text{b}}} V_{{\text{s}}}^{2} (3V_{{\text{c}}}^{2} - 4V_{{\text{s}}}^{2} )}}{{V_{{\text{c}}}^{2} - V_{{\text{s}}}^{2} }} = \frac{{\rho \left( {3\left( {\frac{{\Delta t_{{\text{s}}} }}{{\Delta t_{{\text{c}}} }}} \right)^{2} - 4} \right)}}{{\left( {\frac{{\Delta t_{{\text{s}}} }}{{\Delta t_{{\text{c}}} }}} \right)^{2} - 1}} \times 1.34 \times 10^{10} \,\,\,\,\,\,\,\,\,(psi)$$

(1)

$$K_{{{\text{dyn}}}} = \frac{1}{{c_{{\text{b}}} }} = 1.34 \times 10^{10} \times \rho_{{\text{b}}} \left( {\frac{1}{{\Delta t_{{\text{c}}}^{2} }} - \frac{4}{{\Delta t_{{\text{s}}}^{2} }}} \right)\,\,\,\,\,\,\,\,\,\,\,\,(psi)$$

(2)

$$G_{{{\text{dyn}}}} = 1.34 \times 10^{10} \times \frac{\rho b}{{\Delta t_{{\text{s}}}^{2} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(psi)$$

(3)

$$\nu_{{{\text{dyn}}}} = \frac{{V_{{\text{c}}}^{2} - 2V_{{\text{s}}}^{2} }}{{2(V_{{\text{c}}}^{2} - V_{{\text{s}}}^{2} )}} = \frac{{\left( {\frac{{\Delta t_{{\text{s}}} }}{{\Delta t_{{\text{c}}} }}} \right)^{2} - 2}}{{2\left( {\left( {\frac{{\Delta t_{{\text{s}}} }}{{\Delta t_{{\text{c}}} }}} \right)^{2} - 1} \right)}}$$

(4)

The units of density ($\rho$), travel time of compressional wave (t_r), and travel time of shear wave (t_s) are (g/cm³), $({\raise0.7ex\hbox{${\mu s}$} \!\mathord{\left/ {\vphantom {{\mu s} {ft}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ft}$}})$, and, respectively. The initial parameter for pursuing the equations is Dt, obtained from the DSI (Dipole Shear Sonic Image) Log. Since only the passing time of the pressure waves were recorded in the acoustic logs, Shahbazi and Nabaei represented the following regression correlations for geological formation (Nabaei et al. 2009):

$$\Delta t_{{\text{s}}} = 1.7891\Delta t_{{\text{c}}} + 7.622$$

(5)

$$\Delta t_{{\text{s}}} = 2.5316\Delta t_{{\text{c}}}^{0.9317}$$

(6)

Using the above equations, data are calculated dynamically which is not applicable for direct use in the construction geomechanical model. Therefore, they have to be transformed into static data using computational changes. So, the transforming ratio from dynamic to static based on Wang correlation relations is as follows (Khoshnevis-zadeh et al. 2019; Wang et al. 2017):

$$E_{{{\text{sta}}}} = 0.4145E_{{{\text{dyn}}}} - 1.0593\sqrt {a^{2} + b^{2} }$$

(7)

$$K_{{{\text{sta}}}} = \frac{{E_{{{\text{sta}}}} }}{{2(1 + \nu_{{{\text{sta}}}} )}}$$

(8)

$$G_{{{\text{sta}}}} = \frac{{E_{{{\text{sta}}}} }}{{3(1 - 2\nu_{{{\text{sta}}}} )}}$$

(9)

$$\nu_{{{\text{sta}}}} = 0.79\nu_{{{\text{dyn}}}}$$

(10)

Geomechanical parameters of geological formation rock

Uniaxial pressure resistance

One of the important parameters in evaluating wellbore instability by failure criteria is uniaxial compressive strength which is achieved using uniaxial compression test on the cores. Considering the inaccessibility of information regarding the uniaxial compressive strength of the cores, this parameter has been calculated using the following experimental correlations for southwest oilfields of Iran (Li et al. 2012):

$${\text{UCS}} = e^{{ - 0.633 + \frac{246.540}{{\Delta t_{{\text{c}}} }}}}$$

(11)

$${\text{UCS}} = \frac{{\left( {\frac{7682}{{\Delta t_{{\text{c}}} }}} \right)^{1.82} }}{145}$$

(12)

$${\text{UCS}} = 356.003 + 44.58\ln \left( {\frac{{\rho_{{\text{b}}} }}{{\Delta t^{2} }}} \right)$$

(13)

UCS is the uniaxial compressive strength in MPa, $\Delta t_{{\text{c}}}$ is the travel time of pressure wave in µs/ft, and $\rho_{{\text{b}}}$ is formation density in g/cm³. Since each of the above correlations can correctly estimate the UCS, in order to determine the uniaxial compressive strength accurately, their average value is considered.

Tensile strength of geological formation

Rock tensile structurally ranges from $\frac{1}{8}$. to $\frac{1}{12}$. of UCS resistance. Tensile strength is considered $\frac{1}{10}$ of UCS in this study.

$$t. = 0.1{\text{UCS}}$$

Shear strength of geological formation

Coulomb predicted that the resistance of earth’s materials against shear stress (shear resistance) is the result of two factors:

• 1- Cohesion between components: C

• 2- Friction between components: $\sigma \tan \phi$

There is resistance against shear stress of cohesion and friction components at the threshold of failure. But only the cohesion component and friction component are active before and after the failure.

Angle of internal friction (friction angle)

Frictional component of resistance is completely dependent on the perpendicular stress on the hypothetical shear surface inside rock. It is common to use the friction angle of rock or soil $\left( \phi \right)$ instead of the friction coefficient $\left( \mu \right)$. Angle of internal friction refers to “the resistance of a unit of rock or soil against the shear stress”. In other words, it is an angle that rocky materials (under the hypothetical assumption of no cohesion) collapse as soon as being exposed to this angle. Consequently, many experimental correlations have been developed to calculate the angle of internal friction. In this study, the utilized estimation equation is as follows (Aadnoy and Ong 2003):

$$\phi = 26.5 - 37.4(1 - {\text{NPHI}} - V_{{{\text{shale}}}} )) + 62.1(1 - {\text{NPHI}} - V_{{{\text{shale}}}} )^{2}$$

(14)

where $V_{{{\text{shale}}}}$ is the volume of shale and NPHI is porosity from neutron log. It is worth mentioning that the volume of shale has been calculated using the following correlation and Corrected Gamma Ray (CGR) log:

$$V_{{{\text{shale}}}} = \frac{{{\text{CGR}} - {\text{CGR}}_{\min } }}{{{\text{CGR}}_{\max } - {\text{CGR}}_{\min } }}$$

(15)

Cohesion

The cohesion component of resistance (C) is independent of the normal stress, and its value is considered constant. It is calculated using the following equation, which is derived from Mohr–Coulomb theory:

$$C = \frac{{{\text{UCS}}(1 - {\text{Sin}} \phi )}}{{2{\text{Cos}} \phi }}$$

(16)

Pore pressure

The pressure applied by these fluids is called pore pressure. The pore pressure of the fluid column weight in D meters depth is calculated using the following equation:

$$P_{{\text{P}}} = \int {_{.}^{D} } \rho_{{\text{f}}} \left( z \right)g\,\,\,{\text{d}}z$$

(17)

where $\rho_{{\text{f}}}$ is the fluid density, g the acceleration of gravity of Erath, and Z is the height of the fluid column. The normal gradient of pore pressure is considered 0.365 $\,\,{\raise0.7ex\hbox{${psi}$} \!\mathord{\left/ {\vphantom {{psi} {ft}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ft}$}}$ for the geological formation (He et al. 2017).

Eaton

In this section, the Eaton method is used to predict the pore pressure using an acoustic log. Eaton estimates pore pressure using the ratio of normal acoustic travel time to the travel time of sound. In order to estimate the pore pressure accurately, normal gradient of pore pressure has been corrected using Eaton’s correlation to acoustic log (Feng and Gray 2016b):

$$P_{{\text{P}}} = S - (S - P_{{\text{n}}} )\left[ {\frac{{\Delta t_{{\text{n}}} }}{{\Delta t_{0} }}} \right]^{3}$$

(18)

P_p is pore pressure in MPa, S is perpendicular stress in MPa, P_n is the normal gradient of pore pressure in ${\raise0.7ex\hbox{${psi}$} \!\mathord{\left/ {\vphantom {{psi} {ft}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ft}$}}$ and $\Delta t_{{\text{n}}}$ the travel time of normal sound in ${\raise0.7ex\hbox{${\mu s}$} \!\mathord{\left/ {\vphantom {{\mu s} {ft}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ft}$}}$ and $\Delta t_{0}$ is travel time of sound in ${\raise0.7ex\hbox{${\mu s}$} \!\mathord{\left/ {\vphantom {{\mu s} {ft}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ft}$}}$. The passing time of normal sound $\Delta t_{{\text{n}}}$ is obtained by drawing $\Delta t_{0}$ versus depth as shown in Fig. 4 and finding a regression correlation between these two values (Here, the value translated is 0.0167 µs/ft).

Fig. 4

Pore pressure obtained by repetitive well test

The repeat formation tester (RFT)

The data of the RFT diagram are used in this method. Therefore, the designated tools allow formation fluid invasion inside a reservoir with zero pressure in specific conditions while the tool records the changes of the pressure from zero to the final equilibrium pressure based which is the pore pressure of geological formation concurrently. The final reading of this diagram is the same as the pore pressure every time the reservoir is opened. Figure 5 shows the pressure diagram of RFT tool.

Fig. 5

The diagram of the pressure of reading time in 2752 m depth by the RFT tool

In the target well, the formation pressure was only obtained at limited points shown in Table 1:

Table 1 Geological formations pressure in different depths based on psi

Forecast mud weight method

This method which is usually used for known oilfields, mud engineers, with full knowledge, of the mechanical conditions of geological formation and critical failure pressure calculate mud pressure usually 200 psi more than geological formation pressure. Therefore, it is possible to calculate pore pressure through mud pressure with good accuracy. It is worth mentioning that this method is mostly used for overbalanced drilling. It is not practically suggested for fractured zones.

In-situ stress

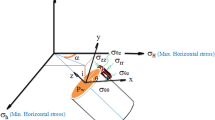
In-situ stress is one of the most important factors effective on wellbore stability and has complex origin (including geological formation weight, tectonic movements, magma masses and…). Estimating the value and the direction of the in-situ stress is mostly possible using acoustic and density logs. The underground formation is influenced by different pressures from the weight of the upper layers and horizontal pressures of the earth and is expressed vertical stress, maximum horizontal stress, and minimum horizontal stress. Figure 6 provides a schematic of these stresses (He et al. 2017).

Fig. 6

In-situ stress existing in the Earth before drilling

In-situ vertical stress

Vertical stress $\left( {S_{\upsilon } } \right)$ is one of the main stresses resulted from the weight of the upper layers and is calculated by rock density integration from the surface to the depth as follows:

$$S_{\upsilon } = \int {_{.}^{z} } (z)g\,\,\,dz \cong \overline{\rho }\,\,gz$$

(19)

where $\rho$ is rock density, g is gravity acceleration, $\overline{\rho }$ is mean overburden density and z is depth. Mean density’s unit is 2.56 g/cm³ in this formation. Figure 7 shows the density log and the vertical in-situ stress in Asmari geological formation.

Fig. 7

Density log and vertical in-situ stress

Minimum horizontal stress

If the horizontal stresses were to be considered as effective stresses, they will only be a function of vertical stress as follows (Li and Purdy 2010):

$$S^{\prime}_{{\text{h}}} = k_{0} S^{\prime}_{\upsilon }$$

(20)

where k₀ is the ratio of in-situ vertical stress and is calculated as follows:

$$k_{0} = \frac{\upsilon }{1 - \upsilon }$$

(21)

And $S^{\prime}$ is the minimal effective horizontal stress. It is possible to correlate the minimum stress using pore pressure parameters P_P, vertical stress $S_{\upsilon }$, Biot coefficient α and Poisson’s ratio:

$$S_{{\text{h}}} = \frac{\upsilon }{1 - \upsilon }\left( {S_{\upsilon } - \alpha P_{{\text{P}}} } \right) + \alpha P_{{\text{P}}}$$

(22)

If extra tectonic strains are applied to the formation of rock, these strains apply extra stress to the rock that can be calculated using the following equations (Mody and Wang 2008):

$$\Delta S_{{\text{h}}} = \frac{E}{{1 - \upsilon^{2} }}\varepsilon_{{\text{h}}} + \frac{E\upsilon }{{1 - \upsilon^{2} }}\varepsilon_{{\text{H}}}$$

(23)

It is worth mentioning that Young's modulus and Poisson’s ratio are static. Now minimum horizontal stress is defined as following:

$$S_{{\text{h}}} = \frac{\upsilon }{1 - \upsilon }\left( {S_{\upsilon } - \alpha P_{{\text{P}}} } \right) + \alpha P_{{\text{P}}} + \frac{E}{{1 - \upsilon^{2} }}\varepsilon_{{\text{h}}} + \frac{E\upsilon }{{1 - \upsilon^{2} }}\varepsilon_{{\text{H}}}$$

(24)

Figure 8 shows the changes of minimum horizontal stress. Biot coefficient $\left( \alpha \right)$ is defined as follows (Hareland and Dehkordi 2007):

$$\alpha = 1 - \frac{{K_{{\text{b}}} }}{{K_{{\text{g}}} }}$$

(25)

where k_b is the bulk modulus of drained porous rock and k_g is bulk modulus of the rock mass solid particles. If it is zero, it means that the rock porosity is almost zero and if its value is 1 it shows a completely porous environment.

Fig. 8

Minimum horizontal stress

Maximum horizontal stress

It is hypothesized that there is a specific correlation between vertical stress and maximum and minimum horizontal stresses in geological formation in balanced conditions. Generalization of Hooke’s law to stresses and pore pressure, maximum horizontal stress is obtainable using the following correlation (Chen et al. 1996; Soleimani et al. 2018):

$$S_{{\text{H}}} = \frac{{S_{{\text{h}}} - \alpha P_{{\text{P}}} }}{\upsilon } - S_{\upsilon } + 2\alpha P_{{\text{P}}}$$

(26)

Three main stresses $S_{\upsilon }$, $S_{\rm h}$ have to be measured to balance the stress–strain using Hooke’s law. Considering Hooke’s law, maximum horizontal stress is written below (poroelastic correlation):

$$S_{{\text{H}}} = \frac{\upsilon }{1 - \upsilon }(S_{\upsilon } - \alpha P_{{\text{P}}} ) + \alpha P_{{\text{P}}} + \frac{\upsilon E}{{1 - \upsilon^{2} }}\varepsilon_{{\text{h}}} + \frac{E}{{1 - \upsilon^{2} }}\varepsilon_{{\text{H}}}$$

(27)

$\varepsilon_{{\text{h}}}$ and $\varepsilon_{{\text{H}}}$ are strain in $\varepsilon_{{\text{h}}}$ and $\varepsilon_{{\text{H}}}$ direction, respectively, and can be compressional or tensile. Since failure usually happens in $S_{{\text{h}}}$’s direction, no strain will occur in this direction and it is possible to ignore $\varepsilon_{{\text{h}}}$ or consider it so negligible due to the fact that the highest strain value will be in S_H’s direction_. These parameters are necessary to calibrate horizontal stress diagram in oilfields under tectonic stresses (like the most south west oilfields in Iran). Minimum horizontal stress has to be calibrated using like Minifrac test or leak off test results, so that first S_H = S_h is placed and then the values of $\varepsilon_{{\text{h}}}$ and $\varepsilon_{{\text{H}}}$ strains are changed to make the curve of the minimum stress fit with these values as much as it is possible. $\varepsilon_{{\text{h}}} = 10^{ - 2}$ and $\varepsilon_{{\text{H}}} = 1.75$ have been calculated. As mentioned above, $\varepsilon_{{\text{h}}}$ is negligible and near zero. Then, maximum and minimum horizontal stresses are calculated as illustrated in Figs. 9 and 10.

Fig. 9

Maximum horizontal stress

Fig. 10

Stresses around wellbore

Stresses around wellbore

Stresses induced around wellbore are expressed as three types of tangential stress, axial stress and radial stress. The results are known as Crash equations (Fjær et al. 2008; Hassani et al. 2017).

According to Fig. 11, there is no shear stress and ($\sigma_{z} ,\sigma_{\theta } ,\sigma_{r}$$\sigma_{r}$) are main stresses which may be directly used in failure criterion. Among induced stresses, tangential stress ($\sigma_{\theta }$) considered as main maximum stress, axial stress $\left( {\sigma_{z} } \right)$ considered as medium main stress and radial stress $\left( {\sigma_{r} } \right)$ considered a minimum main stress.

Fig. 11

A schematic view of in-situ and induced stresses and pore pressure (Khoshnevis-zadeh et al. 2019)

Tangential and axial stresses are a function of $\theta$. This angle shows the direction of stresses around wellbore and it ranges from 0° to 360°. Observing the mentioned correlations, when $\theta$ = 0 or $\theta = \pi$, tangential and axial stresses are minimum and when $\theta = \pm \frac{\pi }{2}$ tangential and axial stress have their maximum values. The minimum and maximums values of tangential and axial stresses for each of in-situ stresses are considered.

$$\theta = 0,\;\theta = \pi \to \sigma_{\theta \min } = 3S_{{\text{H}}} - S_{{\text{h}}} - P_{{\text{W}}} - P_{{\text{P}}}$$

(28)

$$\theta = \pm \frac{\pi }{2} \to \sigma_{\theta \max = } = 3S_{{\text{h}}} - S_{{\text{H}}} - P_{{\text{W}}} - P_{{\text{P}}}$$

(29)

$$\theta = 0,\;\;\theta = \pi \to \sigma_{z\min } = S_{\upsilon } - 2\upsilon \left( {S_{{\text{H}}} - S_{{\text{h}}} } \right) - P_{{\text{P}}}$$

(30)

$$\theta = \pm \frac{\pi }{2} \to \sigma_{z\max } = S_{\upsilon } + 2\upsilon \left( {S_{{\text{H}}} - S_{{\text{h}}} } \right) - P_{{\text{P}}}$$

(31)

Drilling mud pressure (P _w)

The density of the drilling mud may be variable depending on the dissolved nitrogen in the considered geological formation. In this study, the default value of density was selected in such a way that the mud weight would create an equilibrium with the formation pressure this value can be less than the default value based on the deliverability. Therefore, the weight of the mud will create a pressure of 17.8 MPa and mud density is 0.63 g/cm³. Generally, it is possible to calculate the pressure of corresponding to the mud as shown below:

$$P_{{\text{W}}} = \frac{{M_{{\text{W}}} \times g \times D}}{1000}\;\;\;\;({\text{Mpa}})$$

(32)

where M_w is the density of drilling mud, and g is the acceleration of earth gravity in m s².

The following diagram shows maximum and minimum induced stresses and are specified in Figs. 12 and 13.

Fig. 12

The maximum induced stresses

Fig. 13

Minimum induced stresses

Well stability analysis using Mohr–Coulomb failure criterion

Mohr–Coulomb failure Criterion is the most common linear failure model and usually the well stability is analyzed using Mohr–Coulomb failure Criterion. Considering the concept of effective stress, Mohr–Coulomb failure Criterion will be written as (Hussain and Ahmed 2018):

$$\left( {\sigma_{1} - P_{{\text{P}}} } \right) - C_{0} + q\left( {\sigma_{3} - P_{{\text{P}}} } \right)$$

(33)

Mohr–Coulomb Criterion is expressed as follows:

$$\sigma_{1} = C + q\sigma_{3}$$

(34)

where C constant is:

$$C = C_{0} - P_{{\text{P}}} (q - 1)$$

(35)

C₀ is the same as UCS in the above equation and q is specified using the following equation:

$$q = \tan^{2} \left( {\frac{\pi }{4} + \frac{\phi }{2}} \right)$$

(36)

$\phi$ is friction internal angle.

After calculating the mentioned parameters, it is possible to calculate the lowest and the highest allowed drilling mud pressure of corresponding to the shear and tensile failures using Tables 2 and 3.

Table 2 The lowest and the highest allowed level of mud pressure for shear failures

Table 3 The lowest and the highest allowed level of mud pressure for tensile failures

Well stability analysis using Mogi-Coulomb failure criterion

Al-Ajmi and Zimmerman introduced Mogi-Coulomb failure criterion for wellbore stability. It was observed that Druker–Prager criterion estimates values more than the actual rock resistance and Mohr–Coulomb criterion estimates it less than the actual rock resistance. Therefore, they concluded that Mogi-Coulomb criterion is the best option. As mentioned, Mogi-Coulomb failure criterion s also considers the effect of the mean stress. Using the concept of effective stress, Mogi-Coulomb criterion will be as follows(Regel et al. 2017):

$$(I_{1}^{2} - 3I_{2} )^{\frac{1}{2}} = a^{\prime} + b^{\prime}(I_{1} - \sigma_{2} - P_{{\text{P}}} )$$

(37)

where:

$$a^{\prime} = 2c\,\,\,\cos \phi ,\;b^{\prime} = \sin \phi$$

Main stresses ($\sigma_{z} ,\sigma_{\theta }$ & $\sigma_{r}$) are used for three permutations, the first and the second stress constants have similar shapes in all conditions for shear failure models SWBO, SSKO and SLAE which is in conjunction with the lowest allowed level of mud pressure in shear failures and only main mean stress changes in the equation. By adding the first and the second constant:

$$I_{1} = A + B$$

(38)

$$I_{2} = AB + AP_{{\text{W}}} - P_{{\text{W}}}^{2}$$

(39)

By placing the equations in Mogi-Coulomb Failure Criterion, an equation with two roots for P_w is developed. Two roots are obtained in each of the equations and since the lower limit is considered for mud, the smallest positive root is chosen.

After calculating the lowest limit for the mud pressure, main stresses ($\sigma_{z} ,\sigma_{\theta }$ & $\sigma_{r}$) used for three permutations, first and second stress constants have the similar shapes in all conditions for shear failure models SNBO, SDKO and SHAE responding to the lowest allowed level of mud pressure in shear failures and only main mean stress changes in the equation. The first and the second stress constants are:

$$I_{1} = D + E$$

(40)

$$I_{2} = DE + DP_{{\text{W}}} - P_{{\text{W}}}^{2}$$

(41)

By placing the equations in the Mogi-Coulomb failure criterion an equation is resulted with two roots for P. similarly, two roots are obtained in each equation but this time the highest limit considered for mud pressure, and thus the largest positive root is chosen. Table 4 shows the results of the least and the highest allowed level for mud pressure for different types of shear failure.

Table 4 The lowest and the highest allowed level of mud pressure for shear failures by Mogi-Coulomb Failure Criterion

The correlations are related to the lowest and the highest allowed level of mud pressure for tensile failure models based on Mogi-Coulomb criterion equivalent to Mohr–Coulomb criterion as in Table 3 (Gholami et al. 2014; Maleki et al. 2014; Zoback et al. 1986).

Results

Safe weight window and drilling mud stability

Mud weight has a significant role in wellbore stability problems. If the weight of the mud is lower than the desired value, failure will happen. On the other hand, high mud weight may cause mud loss and mechanical pipe sticking. When mud weight is designed for wellbore, it is necessary to select its density in such a way that its corresponding pressure would be higher than the pore pressure and less than geological formation’s failure pressure. All equipment may get stuck inside the well during drilling operations which is mainly due to incorrect mud weight.

Selecting the correct mud weight safety window and its stability can reduce so many problems resulted from mud weight during drilling. The safe mud weight range is when the mud pressure is between the pore pressure and the minimum horizontal stress. When the pressure of the mud is less than the pressure of the formation, fluid suddenly flows in the well from the reservoir which is called a blowout. Also, there is no chance of formation failure or collapse in the safe range and there is low possibility of a breakout. If the mud pressure exceeds the minimum horizontal stress, tensile failures created from drilling and mud loss may occur. The stable range of the mud weight safety window is between the minimum drilling mud weight (preventing breakout) and minimum horizontal stress. Geomechanically, wellbore is created by tensile failures of pipes that are stuck as a result of high mud weight in the stable range of drilling mud and also shear failures are safe and stable which is due to low mud weight.

The maximum and minimum weight of the mud is determined considering the tensile and shear failures. The maximum mud weight is determined considering mud pressure needed for tensile failures and the minimum mud weight is determined considering mud pressure needed for shear failures. Figure 14 shows a schematic view of the drilling mud weight range.

Fig. 14

Drilling mud weight safety range (Zoback 2010)

Determining drilling mud safe window using Mohr–Coulomb criterion

In order to determine the safe mud weight window and its stability, it is necessary to first determine the type of shear and tensile failure in the wellbore. Considering Figs. 12 and 13 the following correlation is created between induced stresses:

$$\sigma_{\theta } > \sigma_{z} > \sigma_{{\text{r}}}$$

Comparing correlations with Table 2 shows that the most common shear failures are wide shear failures. Therefore, the lowest level of mud pressure is determined using this type of failure. Also Considering Figs. 12 and 13 the minimum induced stress is radial stress $\left( {\sigma_{{\text{r}}} } \right)$, thus comparing the minimum induced stress with Table 3 shows that the main tensile failures in the well are radial. Since tensile failures have a higher pressure than shear failures, the maximum mud pressure is always obtained by the vertical failure which is remembered as the hydraulic failure pressure. Figure 15 shows drilling mud window.

Fig. 15

The safe window of mud weight and its stability using Mohr–Coulomb criterion

Discussion

Well stability analysis using FLAC

Numerical methods have been significantly developed in rock mechanics. Numerical modeling is a valuable tool to underrated rock mass behavior, stress redistribution, studying failure mechanism and failure areas and also predicting the transformations resulted from drilling.

FLAC software presents a graphical overview of the stress distribution based on which the locations of the washed-out regions can be determined. Also, it can illustrate the wellbore’s deformation and the well parts’ displacement.

FLAC has been based on FDM and has been written for engineering computations and analyses. Lagrange explicit computational design and mixing-separating weighting method have been used in FLAC to correctly model plastic and flow collapse. 3D computations are done without a need for high memory because stiffness matrix is not formed in this method (Wang et al. 2017). Automatic inertia survey and automatic damping do not influence the failure model and the explicit formulation problem (the limitations of small times and damping essentials) is compensated. FLAC is an ideal analysis tool to solve geotectonic engineering issues. Considering the boundary conditions and the initial stress conditions, nodes displacement is calculated. These computations will begin from the border of model, since stress and initial displacements have been applied on the border. In order to use the software to simulate the models three basic components have to be specified:

• 1. Structural behavior and materials characteristics:

  The network and zoning are completed in this section, which establish the geometric shape and structure of the model. The mesh and mesh sizes are defined in the following sections.

• 2. Boundary and initial conditions

  The mobility of the research area determines the link between the model and the environment. FLAC considers its starting state, which is the same as the state of stagnation. The environment’s physical and behavioral features, such as the friction coefficient, the shear model, the compressive model, and the pore pressure, must subsequently be defined.

• 3. Finite difference network

For analyzing purposes, initially the geometry of the problem is defined. If there is discontinuity in the mold, after the geometry creating phase the necessary properties are allocated to that section. Next, it is time to define behavioral model and apply the properties of materials. Then, the boundary and initial conditions are applied. The model has to be balanced under the existing condition. After creating the balance, now it is time to drill the well. But one has to consider that it is necessary to set all displacements to zero before drilling the well after making sure of the initial balance, because this prevents the inference of displacements before and after drilling of the well. Software input parameters are: in-situ stresses, cohesion, angle of friction, shear modulus, bulk modulus and Poisson’s ratio. Mohr’s model is used in this software which was completely covered in previous parts.

As mentioned in geological setting, the lithology of the well includes layers of lime rock and dolomite and a cross-section is considered in each layer for 2D analysis. Table 5 shows the geomechanical characteristics and also stresses applied to it.

Table 5 The geomechanical characteristics of geological formation and stresses applied to wellbore in four different depth ranges

Then, the 2D model of well-constructed using the above table. Figures 16 and 17 show the conditions of plastic areas around well in different depths.

Fig. 16

The conditions of plastic areas around well in 2861.2 m depth. a Structure around well. b Elastoplastic condition areas around well. c The hydrostatic pressure from inside the well. d Displacement Vector.

Fig. 17

The conditions of stress distribution and displacement areas around well in 2861.2 m depth. a Maximum main stress around the well. b Effective shearing stress along X axis. c Effective horizontal stress. d Displacement in vertical axis

The initial step for the modeling of the wellbore shape alteration is meshing (dividing the environment into small components). Therefore, the environment under investigation divided into small parts (meshes) using elements and nodes. To analyze well stability, the dimensions of the structured model e 100 cm × 100 cm and each of the coordinate axes has been divided into 100 parts. That makes the size of each element 1 cm × 1 cm which is shown in Fig. 16a. Mesh sizes must be selected to cover the entire events of the formation with minimal computational cost, meaning that although an extra small mesh accurately accounts for every event, it is not the optimal size due to the lengthy run-time of the simulation. Since the main unit for the geological logs that are indicative of wellbore stability, such as image logs is centimeters, the mesh sizes were selected within that range.

In Fig. 16b, the pink sections indicate elastic behavior, while the brown and purple sections demonstrate plastic behavior and the elastic yield in plastic behavior, respectively. The frequency of plasticization at 90 and 270 degrees, as well as the transition zone, are shown in this figure. As is observed, UBD is not appropriate in the circumstances with expanding plastic zones. ‏ Fig. 16c illustrates the hydrostatic pressure distribution of the drilling mud in the borehole. The yellow vectors depict the direction and magnitude of the drilling mud pressure. According to this figure, the maximum hydrostatic pressure is applied clockwise at 0 and 180-degree angles. It has a minimum value of 45,135,225 and 315 degrees. The small squares are the mesh network created by the software. The yellow lines indicate the quantity and the direction of the mud pressure which is applied to the wellbore. The displacement vector in the borehole section is illustrated in Fig. 16d. Maximum stresses are applied at 90 and 270 degrees, leading to maximum deformation and displacement rate at 0 and 180 degrees, revealing the break out of these wellbore regions. The density of vectors is moderate in other areas, but the size of vectors indicating the amount of displacement is larger in areas prone to gaps. It is clear that fluid exchange between wells and formations is significant along these vectors, confirming the need for UBD. As is observed, the change of direction in the vectors is smoother and less frequent as the distance from the well increases. The following figures show the direction of the drilling mud pressure displacement along the horizontal and vertical axes, effective stress and strain along horizontal and vertical axes, pore pressure and maximum and minimum stress in different depths.

In Fig. 17a pink areas can handle a maximum pressure of 180 Gpa. It can be observed that the orientation of the maximum stress is perpendicular to the orientation of the minimum stress (the blue area in Fig. 17a). The maximum stress contours surrounding the well are symmetrical since the well is in a tectonic stress field. The blue line represents the minimal stress, which generally results in more deformation. The deformation rate is relatively low in pink, purple, brown, and yellow areas, indicating that these areas are prone to break out due break out in blue color area. Maintaining the stability of the wellbore with drilling fluid is very challenging in these regions; therefore, equilibrium drilling techniques must be adopted. The effective shear stress along the horizontal axis is shown in Fig. 17b. Horizontal shear stresses are more significant at 0 and 180 degrees compared to 90 and 270 degrees in this figure, although shear stresses are not significantly different. The shear stress distribution is uniform, which increases the effectiveness of the maximum stress that initiates the breakout. The purple and brown areas indicate higher values. Figure 17c shows the effective horizontal stress along the horizontal axis. The stress value in the purple and brown areas varies between 95 and 97 Gpa While the minimum value is observed in the perpendicular areas (green). Figure 17d shows the displacement in the vertical axis. Displacement diagrams are another manifestation of this form with more zone variety, as can be deduced by the multiple colors. The pink and the brown area show that the maximum displacement is about 0.1–0.2 mm.‏ This displacement has the same orientation as the minimum stress. Then, general results of the well stability analysis are drawn graphically at the threshold of failure in the horizontal profile.

Conclusions

In this work, the ability of UBD to preserve wellbore stability was investigated. The application of UBD’s viability was assessed using the FEM methodology and FLAC software. The primary benefit of this method is that it allows for the analysis of only one well to determine the weight of drilling mud required for the entire field. Considering induced stresses in results section and figures related to induced stresses, even if mud weight is adjusted to be equal or a slightly less than the geological formation pressure, the wellbore will collapse regardless. Thus, the mud weight has to be reduced again, leading to the underbalanced process. Investigating well stability shows while some ranges provide wellbore stability, other ranges may lead to formation collapse and thus the mean mud pressure for suitable balance in the operation is 16.8 MPa. Since this value is unconventional, a special drilling fluid must be used which consists of light gases to form a foam texture to prevent mud loss. On the other hand, it should prevent the collapsed formation parts to form a mud cake thus the circumstances force us to use the UBD approach. In this situation, the reservoir fluid is allowed out of the well controllably. By analyzing the weight of the light fluids, we noted that even a drilling fluid which consists entirely of gasoline will lead to fluid loss. ‘The analyses of the induced fractures showed that the shear fractures were mostly caused by wide shear failures which creates a situation where wellbore stability is almost impossible. It is also worth mentioning that, while investigating the FLAC software shows that the yield point of the wellbore is when the mud pressure 16.8 MPa. Generally, defining the safety window of the mud wight in this well is unconventional which by itself demonstrates both the necessary and the feasibility of the UBD approach. By observing the output images of the FLAC software, we can understand the distribution of the in-situ stresses that are caused by tectonic processes leading to wide shear failures. When the shear stress distribution is uniform, which increases the effectiveness of the maximum stress that initiates the breakout Investigating the geological formation pressure shows that the failures of well or generally reservoir rock are heterogeneous.