Introduction

Being one of the most common well stimulation techniques, hydraulic fracturing improves formation permeability and thereby increases well production. It is critical to be able to accurately estimate the geometry of the fractures formed by this procedure, which consequently allows engineers to correctly forecast its effectiveness, in order to make the right decision so that financial loss can be avoided. Modeling the formation of the fractures initiated by hydraulic fracturing is therefore a crucial technique for controlling fracture characteristics including width, length, and height. Controlling the geometry of the crack is beneficial in a variety of domains including geothermal energy production stimulation and carbon dioxide underground storage (Levasseur et al. 2010; Zimmermann and Reinicke 2010).

Several numerical modeling methods for hydraulic fracturing have been developed, including the finite element method (FEM) (Enayatpour and Patzek 2012), the discrete element method (DEM) models for rock fracturing (Enayatpour et al. 2014; Jing et al. 1993) and propagation of wave in fractured rocks (Chen and Zhao 1998), the extended finite element method (XFEM) simulations of dynamic crack propagation and three-dimensional cracking (Sukumar et al. 2003; Asadpoure et al. 2006; Prabel et al. 2006), the numerical manifold method (NMM) (Li and Zhao 2019), the boundary element method (BEM) formulation is well suited for analysis of cracks in solids (Ang 2013), and phase field method (PFM) (Heider 2021).

A 3D simulation of hydraulic fracturing in multilayer reservoirs was created by Lee et al. (1991) using the finite element approach, with an emphasis on the propagation of hydraulic forces in elastic reservoirs categorization. Lu et al. (2004) conducted a 3D hydraulic fracturing modeling that accounted for radial flow, which improved the accuracy of hydraulic fracturing height estimation. The expanded finite element method was used by Lecampion (2009) to simulate hydraulic fracturing in an impermeable environment. Simoni and Secchi (2003) investigated cohesive fracture propagation in a nonhomogeneous porous under fluid pressure using a re-meshing approach and a staggered solving algorithm. Rho et al. (2017) discovered that the fracture height and fluid efficiency were both controlled by the interface strength. These findings indicated that the beddings must be accounted for in the modeling in order to make a better evaluation of the development of fracture height.

On the other hand, the effect of interfaces on hydraulic fracture behavior was addressed by some authors using pseudo-3D models. Zhang et al. (2018) provided a pseudo-3D model to account for the impact of modulus contrasts on fracture forms and found out that the presence of weaker bedding slowed upward fracture growth, resulting in a stepwise injection pressure associated with discontinuous upward growth. Besides, a change in fracture height was observed for a hydraulic fracture emerging in a layered rock with material property and in situ stress contrasts (Zhang et al. 2017). Tan et al. (2020) studied the interaction between vertical hydraulic fracture and bedding planes and claimed that, due to the low bonding strength, the bedding planes could be easily activated even when the vertical stress differential coefficient was significant. These works demonstrated that the bedding planes showed significant effects on the propagation behavior. As the depth increases, the difference in stress state between the layers is obvious, which therefore influences the hydraulic fracture geometry. Cui and Radwan (2022) determined a correlation between fractures and sedimentary facies. Regarding the modeling of fluid propagation through rock fractures, Safaei-Farouji et al. (2022) used machine learning methods to evaluate the structural CO2 storage capacity in deep saline aquifers.

Linear elastic fracture mechanics (LEFM), elastic–plastic fracture mechanics (EPFM), and cohesive zone method (CZM) are some common fracture propagation mechanisms. The LEFM has been successfully used to describe the mechanics of fractures in brittle rock, but it should not be utilized to describe the mechanics of fractures in ductile rock. Many brittle rocks, however, demonstrate ductility under high temperature and high pressure, according to Atkinson (1989), many brittle rocks exhibit ductility under high temperature and high pressure, so the LEFM is not suitable for hydraulic fracturing because a petroleum well frequently encounters high pressure high temperature due to its significant depth. Liu et al. (2018) also discussed the limits of LEFM in predicting hydraulic fracture height and offered a new chart based on fluid–solid coupling equations and rock fracture mechanics to determine hydraulic fracture height using the extended finite element method (EFEM). Furthermore, the LEFM is restricted to a specific range of stress differentials between the pay-zone and surrounding formations. Additionally, since rock hardness is highly influenced by temperature, as a result the temperature plays an essential role in hydraulic fracturing modeling, which has been largely overlooked in the literature thus far.

The CZM, which incorporated the cohesive elements in a finite element model, was first proposed by Barenblatt (1962) and Dugdale (1960) in the 1960s, but its application in fracture stimulation just recently piqued researchers' interest. Chen et al. (2009) used an interface element regulated by a cohesive law to describe fracture propagation in an impermeable environment and compared the results to analytical solutions in a scenario where rock fracture toughness restricted the fracture development. To examine the impact of rock plasticity, Lobao et al. (2010) used the zero-thickness element method to model both fluid leakage and fracture propagation. Alfano et al. (2007) demonstrated the use of CZM to anticipate fracture initiation and propagation in a variety of materials, including both brittle and ductile materials. CZM was also used by Yao et al. (2010) to model hydraulic fracturing in ductile and quasi-brittle rock. The advantages, limitations, and challenges of CZM were substantially presented in the work of Elices et al. (2002). The singularity at the crack tip region, which presents significant numerical modeling difficulties in classic fracture mechanics, can be avoided using the CZM. Haddad and Sepehrnoori (2015) came to the conclusion that LEFM should be used in the fracture propagation model for brittle rock, while EPFM would be preferred for ductile rock, and CZM was suitable for quasi-brittle rock. This reason explained why CZM was widely selected to simulate the development of hydraulic fracture because the shale can be regarded as quasi-brittle rock. The application of CZM was also seen in the work of Yao (2011) in which the results of CZM were compared to those of pseudo-3D and Perkins and Kern (PKN) models. Carrier and Granet (2012) examined an issue of fluid-driven fracture propagation in a permeable poroelastic media, utilizing a zero-thickness finite element to represent the fracture and a cohesive zone model to control its propagation. Shin (2013) used XFEM to create a 3D model for simultaneous propagation of multiple fractures in a geomechanical model, and discovered that fluid viscosity and fluid flow rate were important factors influencing hydraulic fracture height. To analyze fracture initiation and propagation, Mahdi Haddad and Haddad and Sepehrnoori (2016) proposed a CZM model based on XFEM using ABAQUS. Saberhosseini et al. (2017) used the cohesive zone approach to create a 3D model to study the effects of parameters including Young's modulus, Poisson's ratio, rock fracture toughness, and fracturing fluid viscosity on fractures generated by hydraulic fracturing.

Yi et al. (2020) developed a hydraulic fracture height mathematical model aimed at high stress and multilayered complex formations to predict fracture height in hydraulic fracturing, based on studying the effect of plastic region generated by stress concentration at fracture tip on fracture height growth. The results indicated that the rock's fracture toughness can prevent fracture height from increasing. Zhou et al. (2021) used hydraulic fracturing techniques to create new fracture networks in coal seams with natural fractures. A continuum discontinuum element approach (CDEM) was proposed for simulating and analyzing hydraulic fracture propagation in coal seams. For capturing the deformation and cracking processes of fractured coal, an elastic–damage–fracture model was developed. To mimic the hydro-mechanical coupling processes, a stress–fracture percolation relation was used. The impact of mechanical strengths, distances, and lengths of natural fractures was thoroughly investigated. The findings could be used to improve the fracturing design. Cai et al. (2021) built computational nonhomogeneous enamel models and constructed the fracture element of enamel dumb nodes to accurately solve the fracture parameters of enamel and the energy release rates of the nonhomogeneous enamel structure with cracks. These authors established that the fracture element of the enamel dumb nodes is very accurate, simple, and convenient by comparing them to analytical solutions. Furthermore, rather than being solitary or distinctive elements, the cracks can be other elements, demonstrating adaptability and other benefits. In the work of Gonenli and Das (2022), the cracks are modeled independently to explore the dynamic behavior of the damaged circular constructions, taking into account horizontal and vertical orientations, ten distinct positions, and four fracture sizes. To explore the influence of fracture directions on circular thin plates, vertical and horizontal oriented cracks are inserted in the middle between the outer and inner borders. The finite element method is used to get the first five resonance frequencies, as well as the related mode shapes of the fractured circular and annular plates. According to this research, a crack can change the mode shapes by accumulating bending zones around it, depending on its location and size. Furthermore, a crack can alter the number of bending zones in the mode shapes of circular or annular structures.

A key factor influencing the hydraulic fracturing is the temperature because the properties of injection fluid and formation rock depend on the temperature. Fluid viscosity varies with temperature due to two factors: cohesive force and molecular momentum transfer. In liquids, the cohesive force is the main influence on viscosity because the molecules exert an attractive force on each other through moving layers. Increasing the temperature causes the viscosity to drop because the particles have more thermal energy and can more easily overcome the cohesive force holding them together (Poling et al. 2000; The Engineering ToolBox 2004). The atomic vibrations in the crystal structure increase as the temperature of the material increases, as a result Young's modulus is affected by temperature. The atomic space in the crystal rises as the atomic vibration increases, while the atomic force decreases. The variation of Young’s modulus in function of temperature for various kinds of rock can be obtained from literature review, such as the values of Young’s modulus for sandstone (Wu et al. 2013), granite (Chen et al. 2012), mudstone (Zhang et al. 2013), limestone (Mao et al. 2009), and marble (Zhang et al. 2009). Regarding the fracture toughness of materials exposed to high temperatures, its value will be diminished, consequently reducing the rock's resistance to fracturing. Similarly to Young’s modulus, the variation of fracture toughness in function of temperature for different types of rock can be extracted from literature review. The variation of fracture toughness in function of temperature for various kinds of rock can be obtained from literature review, such as the values of fracture toughness for Westerly granite (Atkinson et al. 1982), sandstone (Feng et al. 2019), black gabbro and Westerly granite (Meredith and Atkinson 1985), stripa granite (Zhang et al. 1998), and BS granite (Wang 2003). On the other hand, the rock’s Poisson's ratio is also affected by temperature. Results from the literature showed that Poisson's ratio of many rocks decreases with increasing temperature (Wingquist 1969). Beside the temperature, the formation permeability also influences the hydraulic fracture process (Salimzadeh and Khalili 2015). Furthermore, the leak-off coefficient is affected not only by the permeability but by the injection fluid viscosity as well (Settari 2013), which in turn is affected by the temperature, and consequently affects the hydraulic fracturing results.

In this paper, the cohesive zone method was used to model the evolution of fracture geometry in time and space and to investigate the influence of the Young’s modulus, the Poisson ratio, the fracture energy, the porosity, and the maximum horizontal stress of the reservoir and of the upper and lower barriers. Regarding the stress state underground, hydraulic fracture normally propagates in the direction of the maximum principal stress. Moreover, the criteria used in this paper for initial damage will require the value of maximum horizontal stress. For these reasons, the maximum horizontal stress was chosen to study the impact of stress state on hydraulic fracture height.

Methodology

Stress equilibrium equation

The effective stress for rock matrix saturated with single-phase fluid is expressed as in Liu et al. (2019) and Biot (1941):

$$\sigma^{^{\prime}} = \sigma + \alpha p_{{\text{m}}} I$$
(1)

where σ′ is the effective stress, Pa; σ is the total stress, Pa; α is the Biot coefficient; pm is the matrix fluid pressure, Pa; I is the second-order identification tensor. The Biot coefficient is given as:

$$\alpha = 1 - \frac{{K_{V} }}{{K_{S} }}$$
(2)

where KV and \(K_{s}\) are the bulk moduli of the porous rock and of the rock matrix material, respectively, Pa. The stress and strain relationship can be expressed in an incremental form as:

$${\text{d}}\sigma^{^{\prime}} = D_{{{\text{ep}}}} \left( {{\text{d}}\varepsilon - {\text{d}}\varepsilon_{1} } \right)$$
(3)

where \(D_{{{\text{ep}}}}\) is the elastic–plastic matrix; \(d_{1}\) is the rock compression strain caused by pore fluid pressure, which can be written as:

$${\text{d}}\varepsilon_{1} = - m\frac{{{\text{d}}\overline{p}}}{{3K_{s} }}$$
(4)

where m = [1; 1; 1; 0; 0; 0].

The virtual work principle can be used to define the stress equilibrium equation of rock. The virtual work of rock is equal to the virtual work generated by the forces operating on the rock (including body force and surface force):

$$\mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} {\text{d}}\sigma \,{\text{d}}V - \mathop \int \limits_{V} \delta u^{{\text{T}}} {\text{d}}f\,{\text{d}}V - \mathop \int \limits_{S} \delta u^{{\text{T}}} \,{\text{d}}\tau {\text{d}}S = 0$$
(5)

where δε is the virtual displacement, m; δu is the virtual strain; \(\tau\) is the surface force, N m−2; f is the volume force, N m−3; dS is the area element, m2; dV is the volume element, m3.

If α = 1; the combination (5) and formula (3) and (1) can be expressed as:

$$\mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} D_{{{\text{ep}}}} \left( {{\text{d}}\varepsilon + m\frac{{{\text{d}}\overline{p}}}{{3K_{s} }}} \right) {\text{d}}V - \mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} m {\text{d}}\overline{p} \,{\text{d}}V - \mathop \int \limits_{V} \delta u^{{\text{T}}} {\text{d}}f\,{\text{d}}V - \mathop \int \limits_{S} \delta u^{{\text{T}}} {\text{d}}\tau {\text{d}}S = 0.$$
(6)

The permeability equation involves time terms, and the virtual work equation's time term is derived in order to connect stress and permeability:

$$\mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} D_{{{\text{ep}}}} \left( {\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} + m\frac{1}{{3K_{s} }}\frac{{{\text{d}}\overline{p}}}{{{\text{d}}t}}} \right) {\text{d}}V - \mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} m \frac{{{\text{d}}\overline{p}}}{{{\text{d}}t}}{\text{d}}V - \mathop \int \limits_{V} \delta u^{{\text{T}}} \frac{{{\text{d}}f}}{{{\text{d}}t}}{\text{d}}V - \mathop \int \limits_{S} \delta u^{{\text{T}}} \frac{{{\text{d}}\tau }}{{{\text{d}}t}}{\text{d}}S = 0.$$
(7)

It is assumed that the pressure of the whole unsaturated zone is fixed, namely \(\frac{{{\text{d}}p_{{\text{a}}} }}{{{\text{d}}t}} = 0\); and the derivative of the average pore fluid pressure to the time is expressed as:

$$\frac{{{\text{d}}\overline{p}}}{{{\text{d}}t}} = \frac{{{\text{d}}\left( {s_{{\text{W}}} p_{{\text{W}}} + \left( {1 - s_{{\text{W}}} } \right)p_{{\text{a}}} } \right)}}{{{\text{d}}t}} = S_{{\text{W}}} \frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}} + P_{{\text{W}}} \frac{{{\text{d}}S_{{\text{W}}} }}{{{\text{d}}t}}.$$
(8)

When the standard atmospheric pressure is \(P_{{\text{a}}} = 0.1\) MPa; the function of the saturation and two variables: capillary pressure and pore water pressure, \(\frac{{{\text{d}}S_{{\text{W}}} }}{{{\text{d}}t}}\) can be expressed as:

$$\frac{{{\text{d}}S_{{\text{W}}} }}{{{\text{d}}t}} = \frac{{{\text{d}}S_{{\text{W}}} }}{{{\text{d}}p_{{\text{W}}} }}\frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}} = \xi \frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}}.$$
(9)

The value of \({\upxi }\) is usually obtained by moisture absorption or drying test of capillary pressure and saturation, and then the relevant curve can be determined. Formula (9) can be expressed as:

$$\frac{{{\text{d}}\overline{p}}}{{{\text{d}}t}} = \left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)\frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}}.$$
(10)

The combination (10) and formula (7) can be expressed as:

$$\begin{aligned} \mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} D_{{{\text{ep}}}} \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} \,{\text{d}}V & + \mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} D_{{{\text{ep}}}} \left( {m\frac{{\left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)}}{{3K_{s} }}\frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}}} \right) {\text{d}}V - \mathop \int \limits_{V} \delta \varepsilon^{{\text{T}}} m\left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)\frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}}{\text{d}}V \\ & = \mathop \int \limits_{V} \delta u^{{\text{T}}} \frac{{{\text{d}}f}}{{{\text{d}}t}}{\text{d}}V - \mathop \int \limits_{S} \delta u^{{\text{T}}} \frac{{{\text{d}}\tau }}{{{\text{d}}t}}{\text{d}}S. \\ \end{aligned}$$
(11)

Continuity equation

The flow of liquid in porous media is Darcy flow. Darcy’s law for the porous medium flow may be written as (Liu et al. 2019):

$$v_{w} = - \frac{1}{{n_{w} g\rho_{w} }}k\left( {\frac{{\partial P_{w} }}{\partial x} - g\rho_{w} } \right)$$
(12)

where \(v_{w}\) is the liquid flow velocity, m s−1; k is the permeability; \(n_{w}\) is the ratio of liquid volume to total volume of rock; \(P_{w}\) is the pressure difference, Pa; \(\rho_{w}\) is the liquid density, kh m−3. According to the principle of mass conservation, for a certain volume of rock, the total mass of fluid flowing into the rock within a certain time is equal to the mass of increment and outflow of the rock. The law of mass conservation for fluid flowing in porous media can be written as follows:

$$\begin{aligned} S_{{\text{W}}} & \left( {m^{{\text{T}}} - \frac{{m^{{\text{T}}} D_{{{\text{ep}}}} }}{{3K_{s} }}} \right)\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} - \nabla^{{\text{T}}} \left[ {k_{0} k_{r} \left( {\frac{{\nabla P_{w} }}{{\rho_{w} }} - g} \right)} \right] \\ & + \left\{ {\xi n + n_{w} \frac{{S_{{\text{W}}} }}{{K_{{\text{W}}} }} + S_{{\text{W}}} \left[ {\frac{{1 - n_{w} }}{{3K_{s} }} - \frac{{m^{{\text{T}}} D_{{{\text{ep}}}} \alpha m}}{{\left( {3K_{s} } \right)^{2} }}} \right]\left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)} \right\}\frac{{{\text{d}}p_{{\text{W}}} }}{{{\text{d}}t}} = 0 \\ \end{aligned}$$
(13)

where \(k_{0}\) is the initial permeability coefficient tensor multiplied by water density; \(k_{r}\) is a specific permeability coefficient, which can be a function of saturation, stress, strain or damage variable; g is the acceleration of gravity, \(n_{w}\) is porosity, and \(K_{{\text{W}}}\) is the bulk modulus of water.

Finite element discretization

The finite element is discrete into the following functional formula:

$$\left\{ {\begin{array}{*{20}l} {u = N_{u} \overline{u}} \hfill \\ {\varepsilon = B\overline{u}} \hfill \\ {P_{w} = N_{p} \overline{P}_{w} } \hfill \\ \end{array} } \right.$$
(14)

where \(\overline{u}\) and \(\overline{P}_{w}\) are the displacement and pore pressure of element nodes, respectively.

When formula (14) is substituted into (13), it can be simplified as:

$$K\frac{{ {\text{d}}\overline{u}}}{{{\text{d}}t}} + C\frac{{{\text{d}}\overline{P}_{w} }}{{{\text{d}}t}} = \frac{{{\text{d}}f}}{{{\text{d}}t}}$$
(15)
$$K = \mathop \int \limits_{V} B^{{\text{T}}} D_{{{\text{ep}}}} B {\text{d}}V$$
(16)
$$C = \mathop \int \limits_{V} B^{{\text{T}}} D_{{{\text{ep}}}} \left( {m\frac{{\left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)}}{{3K_{s} }}} \right)N_{p} {\text{d}}V - \mathop \int \limits_{V} B^{{\text{T}}} \left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right)mN_{p} {\text{d}}V$$
(17)
$${\text{d}}f = \mathop \int \limits_{V} N_{u}^{{\text{T}}} {\text{d}}f {\text{d}}V + \mathop \int \limits_{S} N_{u}^{{\text{T}}} {\text{d}}\tau {\text{d}}S.$$
(18)

The flow boundary is as follows:

$$- n^{{\text{T}}} kk_{r} \left( {\frac{{\overline{N}P_{w} }}{{\rho_{w} }} - g} \right) = q_{w} .$$
(19)

\(n^{{\text{T}}}\) is the element normal direction of the flow boundary, and \(q_{w}\) is the water flow across the boundary within the element time.

The pore pressure boundary is:

$$P_{w} = P_{wb} .$$
(20)

\(P_{wb}\) is the pore pressure value of the known boundary.

When the Galerkin method (Zienkiewicz and Taylor 2005) is used:

$$\mathop \int \limits_{V} a^{{\text{T}}} \overline{A} {\text{d}}V + \mathop \int \limits_{S} b^{{\text{T}}} \overline{B}{\text{d}}S = 0.$$
(21)

a and b are arbitrary functions, \(\overline{A}\) is the governing equation and \(\overline{B}\) is the boundary continuity equation.

When formula (13) is assumed as A, formula (19) as B, and a = − b, then it can be simplified as:

$$E\frac{{ {\text{d}}\overline{u}}}{{{\text{d}}t}} + F\overline{P}_{w} + G\frac{{{\text{d}}\overline{P}_{w} }}{{{\text{d}}t}} = \overbrace {f}$$
(22)
$$E = \mathop \int \limits_{V} N_{p}^{{\text{T}}} S_{{\text{W}}} B\left( {m^{{\text{T}}} - \frac{{m^{{\text{T}}} D_{{{\text{ep}}}} }}{{3K_{s} }}} \right) {\text{d}}V$$
(23)
$$F = \mathop \int \limits_{V} \left( {\nabla N_{p} } \right)^{{\text{T}}} kk_{r} \nabla N_{p} {\text{d}}V$$
(24)
$$G = \mathop \int \limits_{V} N_{p}^{{\text{T}}} \left\{ {S_{{\text{W}}} \left[ {\frac{1 - n}{{K_{s} }} - \frac{{m^{{\text{T}}} D_{{{\text{ep}}}} m}}{{\left( {3K_{s} } \right)^{2} }}} \right]\left( {S_{{\text{W}}} + P_{{\text{W}}} \xi } \right) + \xi n + n\frac{{S_{{\text{W}}} }}{{K_{{\text{W}}} }}} \right\}N_{p} {\text{d}}V$$
(25)
$$\overbrace {f} = \mathop \int \limits_{S} N_{p}^{{\text{T}}} q_{wb} \,{\text{d}}S - \mathop \int \limits_{V} \left( {\nabla N_{p} } \right)^{{\text{T}}} kk_{r} g {\text{d}}V.$$
(26)

When formulas (15) and (22) are combined, the stress–permeability coupling equation is:

$$\left[ {\begin{array}{*{20}c} K & C \\ E & G \\ \end{array} } \right] \frac{d}{dt} \left\{ {\begin{array}{*{20}c} {\overline{u}} \\ {\overline{P}_{w} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & F \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\overline{u}} \\ {\overline{P}_{w} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{{\text{d}}f}}{{{\text{d}}t}}} \\ {\overbrace {f}} \\ \end{array} } \right\}.$$
(27)

Dynamic change equation of rock porosity and permeability.

The porosity and permeability of reservoirs change dynamically with volumetric strain, and these two important parameters should be updated at any time in the calculation process.

$$\varphi = \frac{{\varphi_{0} - \varepsilon_{{\text{V}}} }}{{1 - \varepsilon_{{\text{V}}} }}$$
(28)
$$k = k_{0} \frac{1}{{1 - \varepsilon_{{\text{V}}} }}\left( {1 - \frac{{\varepsilon_{{\text{V}}} }}{{\varphi_{0} }}} \right)^{3}$$
(29)

where φ is the porosity of the rock, non-dimensional; φ0 is the initial porosity of the rock, non-dimensional; \(\varepsilon_{{\text{V}}}\) is the volume strain, non-dimensional; k is the dynamic permeability of rock, µm2; \(k_{0}\) is the initial rock permeability, µm2.

Basic equation of fracture propagation

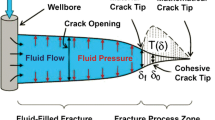
The structure of rock can be idealized as an assembly of pieces stuck together along the boundaries using cohesion and friction. In rock mechanics, the pieces are called fragments and the cohesive zone along the boundaries is called the contact zone. In Fig. 1, the fragments are idealized as mass particles or mass blocks and the contact zone or the potential failure zone is idealized as springs. The rupture of the contacts follows a cohesive zone model which follows a traction–separation law, as shown in Fig. 2.

Fig. 1
figure 1

Illustration of CZM method, extracted from the work of Enayatpour (2015)

Full size image
Fig. 2
figure 2

The quadratic nominal stress traction–separation law (ABAQUS 2016)

Full size image

The cohesive zone method (CZM) can simulate the cohesive elements model for the initial loading, the initiation of damage, and the propagation of damage leading to eventual failure in the material. Unlike the normal element, the cohesive element can be as small as zero before the load is applied. The propagation of the cracks is restricted along the layer of cohesive elements. The advantage of this method is that it does not require an existing fracture. Before the initiation damage of the cohesive elements, the constitutive relation of CZM is linear elasticity, with the elastic behavior described in Eq. 30 (ABAQUS 2016).

$$t = \left\{ {\begin{array}{*{20}c} {t_{n} } \\ {t_{s} } \\ {t_{t} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {K_{nn} } & {K_{ns} } & {K_{nt} } \\ {K_{ns} } & {K_{ss} } & {K_{st} } \\ {K_{nt} } & {K_{st} } & {K_{tt} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{n} } \\ {\varepsilon_{s} } \\ {\varepsilon_{t} } \\ \end{array} } \right\} = K\varepsilon$$
(30)

\(t\) is the cohesive element traction stress vector, dimensionless; \(t_{n}\) is the normal stress, Mpa; \(t_{s} , t_{t}\) are the first shear stress and second shear stress, MPa; \(K_{nn}\) is the Young’s modulus, Mpa; \(K_{ss} , K_{tt}\) are the shear modulus, MPa; \(\varepsilon_{n} ,\varepsilon_{s} ,\varepsilon_{t}\) are the dimensionless strains in normal, first shear, and second shear directions, given in Eq. 31 (ABAQUS 2016).

$$\varepsilon_{n} = \frac{{d_{n} }}{{T_{o} }},\;\varepsilon_{s} = \frac{{d_{s} }}{{T_{o} }},\;\varepsilon_{t} = \frac{{d_{t} }}{{T_{o} }}.$$
(31)

\(d_{n} ,d_{s} ,d_{t}\) are, respectively, the displacements in normal, first shear direction, and second shear direction. \(T_{o}\) is the cohesive element thickness. For 2D simulation, the component of the second shear direction does not exist. The damage in cohesive elements follows the stress traction–separation law, which demonstrates the relation between traction and separation displacement as shown in Fig. 2.

\(t_{n}^{o} ,t_{s}^{o}\), and \(t_{t}^{o}\) represent the peak values of the nominal stress when the deformation is either purely normal to the interface or purely in the first or the second shear direction, respectively. Likewise, \(\delta_{n}^{0} ,\delta_{s}^{o}\), and \(\delta_{t}^{o}\) represent the peak values of the relative displacement when the deformation is either purely normal to the interface or purely in the first or the second shear direction, respectively. Once the separation gets to \(\delta_{n}^{f}\), cohesive element completely fails.

The flow of fluids in hydraulic fracturing includes two flow patterns. Tangential flow is used to describe the fluid flow in fracture and normal flow is used to describe the leak-off of fracturing fluid into the rock matrix as shown in Fig. 3.

$$qd = - k_{t} \nabla p.$$
(32)
Fig. 3
figure 3

Flow model hydraulic fracturing (ABAQUS 2016)

Full size image

For the tangential flow described in Eq. 32, q is the tangential flow rate of the liquid, m s−1; \(\nabla p\) is the tangential flow fluid pressure gradient, Pa/m; d is the fracture aperture, m; \(k_{t}\) is the tangential permeability and is calculated according to Eq. 33 as follows:

$$k_{t} = \frac{{d^{3} }}{12\mu }$$
(33)

where μ is the viscosity of the fracturing fluid (Pa s).

The governing equation of the normal flow is defined in Eq. 34:

$$\left\{ {\begin{array}{*{20}l} {q_{{\text{t}}} = C_{{\text{t}}} \left( {P_{i} - P_{{\text{t}}} } \right)} \hfill \\ {q_{{\text{b}}} = C_{{\text{b}}} \left( {P_{i} - P_{{\text{b}}} } \right)} \hfill \\ \end{array} } \right.$$
(34)

where \(q_{{\text{t}}}\) is the flow rates into the top surface, m s−1; \(C_{{\text{t}}}\) is the leak-off coefficient of the top surface, \({\text{m}}/\sqrt {\text{s}}\), \(C_{{\text{b}}}\) is leak-off coefficients of the bottom surface, \({\text{m}}/\sqrt {\text{s}}\). \(P_{{\text{t}}}\) is the pore pressure on the top surface, Pa; and \(q_{{\text{b}}}\) is the flow rate into the bottom surface, \(P_{{\text{b}}}\) is the pore pressure on bottom surfaces, \(P_{i}\) is the fluid pressure in the fracture, Pa.

Fracture initiation criteria is applied in cases where no initial crack existed in the material. The process of fracturing begins when the stresses and/or strains satisfy certain damage initiation criteria. There are three criteria used for initial damage: maximum principal stress damage (MAXPS) and maximum principal strain damage (MAXPE); maximum nominal stress damage (MAXS) and maximum nominal strain damage (MAXE); quadratic nominal stress damage (QUADS) and quadratic nominal strain damage (QUADE). Fracture evolution was defined as the energy required for the fracture to propagate after the material had been damaged. There are several criteria for evaluating the fracture propagation, among which two standards are often used: Power's law and BK's law (Benzeggagh–Kenane).

The criteria of BK’s law (Benzeggagh and Kenane 1996) was introduced for hydraulic fracturing when initiation fracturing occurs and is represented by Eq. 35:

$$G_{n}^{{\text{C}}} + \left( {G_{s}^{{\text{C}}} - G_{n}^{{\text{C}}} } \right)\left\{ {\frac{{G_{s} + G_{t} }}{{G_{n} + G_{s} + G_{t} }}} \right\}^{\eta } = G^{{\text{C}}}$$
(35)

where \(G_{n} ,G_{s} ,G_{t}\) represent the energy release rates of one normal and two shear directions. The C index represents the critical energy release rate, and η is the property constant of the material. Both normal stress and shear stress are affected by the hydraulic fracturing process. The components of normal stress and shear stress can be described as in Eq. 36 (ABAQUS 2016):

$$\begin{aligned} t_{n} & = \left\{ {\begin{array}{*{20}l} {\left( {1 - D} \right)\overline{{t_{n} }} , } \hfill & {\quad \overline{{ t_{n} }} \ge 0} \hfill \\ {\overline{{t_{n} }} , } \hfill & {\quad \overline{{t_{n} }} < 0} \hfill \\ \end{array} } \right. \\ t_{s} & = \left( {1 - D} \right)\overline{{t_{s} }} \\ t_{t} & = \left( {1 - D} \right)\overline{{t_{t} }} \\ \end{aligned}$$
(36)

where \(\overline{t}\) are the stress components predicted by the elastic traction–separation behavior for the current strains without damage. Here, the indices n, s, t represent, respectively, the normal stress and the two shear stresses. The overall damage in the material is presented by D which captures the combined effects of all active mechanisms. No damage occurs (D = 0) at the start of the simulation. D monotonically evolves from 0 to 1 upon further loading after the initiation of damage. The evolution of the damage variable, D, has the following usual form shown in Eq. 37 (ABAQUS 2016):

$$D = \frac{{\delta_{m}^{f} \left( {\delta_{m}^{\max } - \delta_{m}^{0} } \right)}}{{\delta_{m}^{\max } \left( {\delta_{m}^{f} - \delta_{m}^{0} } \right)}}$$
(37)

Here, \(\delta_{m}^{f}\) and \(\delta_{m}^{0}\) are the displacement components at complete damage and the effective displacement at the initiation of damage, \(\delta_{m}^{\max }\) is the maximum effective displacement.

In the simulation, we will need to use the phantom nodes, which are superposed on the original real nodes, and are introduced to represent the discontinuity of the cracked elements (Meer and Sluys 2009). When the element is intact, each phantom node is completely constrained to its corresponding real node. When the element is cut through by a crack, the cracked element splits into two parts. Each part is formed by a combination of some real and phantom nodes depending on the orientation of the crack. Each phantom node and its corresponding real node are no longer tied together and can move apart.

Simulation procedure

In this study, the hydraulic fracturing process will be modeled using a three-dimensional numerical model of the upper barrier–reservoir–lower barrier as shown in Fig. 4a. The size of this model is 60 m width × 50 m height × 100 m length, with the thickness of the reservoir 10 m and the barriers of 20 m height each. The modeling took into account the variation of rock dynamics, rock porosity, permeability, pore pressure, and fracture surface filtration. The reservoir is the formation rock which contains petroleum products such as oil and gas. The upper and lower barriers are the rock layers situated adjacently above and below the reservoir.

Fig. 4
figure 4

Modeling of hydraulic fracturing: 3D modeling (a) and meshing (b)

Full size image

For the boundary conditions in Fig. 4, no deformation and no displacement in any direction could be observed at the boundary. By providing a layer of elements (potential path) with zero thickness, the cohesive zone model (CZM) is used to represent fracture initiation and growth. When the CZM elements are damaged, they open up and lose their rigidity when they fail, causing the elements to become detached. As a result, the fracture can only spread along the cohesive elements. To minimize mesh dependency, fine mesh should be utilized close to the fractures, while coarse mesh should be used at the reservoir's margins to reduce computational expense (Fig. 4b).

To consider how hydraulic fracturing height is affected under the influence of geomechanical properties of reservoir rock, in this study, a data set for calculation and simulation is used, presented in Table 1. The variation in Young’s modulus of the barriers and of the reservoir will help to explain the results later because it was mentioned in literature review that the interfaces have a clear effect on the propagation behavior of a hydraulic fracture. Teufel and Clark (1984) found out that an increase in minimum horizontal stress could inhibit the vertical growth of the fracture into the barriers zone. Therefore, the influence of minimum horizontal stress will be also included in the sensitivity study of this paper.

Table 1 Basic parameters of numerical simulation model
Full size table

The cases studied in this paper are summarized in Table 2. These case-studies were proposed to effectuate a sensitivity study to understand the influence of uncontrolled parameters such as rock’s properties and stress state.

Table 2 Different cases for the sensitivity study of various parameters
Full size table

Results and discussion

Impact of the Young’s modulus on the hydraulic fracture height

To study the impact of Young’s modulus on the hydraulic fracture height, we should distinguish Young’s modulus values of the reservoir and the upper and lower barriers. In case 1, we consider the same Young’s modulus values for the beddings (15 GPa) while varying the values of the formation from 10 GPa (lower than the beddings’ Young’s modulus) to 15 GPa (equal to the beddings’ values) and finally to 20 GPa (higher than the beddings’ values). The simulation results for these different scenarios in case 1 are presented in Figs. 5, 6, and 7, respectively. It is noted that the scenario where Young’s modulus of the reservoir is equal to 20 GPa is also the basic case 0.

Fig. 5
figure 5

Hydraulic fracturing height for case 1a at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image
Fig. 6
figure 6

Hydraulic fracturing height for case 1b at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image
Fig. 7
figure 7

Hydraulic fracturing height for case 1c, which is also the basic case, at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image

To facilitate the analysis of the results, Fig. 8 presents the summary of the development of fracture height of case 1 in the function of time. At first, it is observed that the fracture height increases rapidly at time step 10 and 20. It seems that the higher the reservoir’s Young’s modulus is, the faster the fracture height develops at the first stage. However, the fracture height stagnates once it reaches the reservoir thickness, independently of the value of the reservoir’s Young’s modulus. The explanation here is that the upper and lower barriers constitute two interfaces to constrain the fracture’s height development. It is remarked that after the stagnation, only if Young’s modulus of the reservoir is higher than the ones of the beddings, the fracture breaks through the interface and propagates into the beddings. In the other cases, the fracture just develops along with the interfaces between the reservoir and the barriers. The following suggestion for the application of hydraulic fracturing, in reality, can be deduced from these interesting results: if Young’s modulus of the reservoir is higher than the ones of the bedding, it is highly possible that the hydraulic fracture will propagate into adjacent layers; hence, caution measures must be taken in order to avoid the water flooding (the fracture penetrates into the water aquifer) or unwanted gas production problems (the fracture develops up into the gas layer).

Fig. 8
figure 8

Development of fracture height for different values of reservoir’s Young’s modulus

Full size image

The results from case 1 demonstrated the difference in Young’s modulus of the reservoir and the beddings influenced the fracture height. To verify this hypothesis, we conducted another case study (case 2) in which Young’s modulus of the reservoir (20 GPa) is higher than the one of the upper bedding (15 GPa) but lower than the one of the lower bedding (25 GPa). Figure 9 presents the development of fracture height over time for case 2.

Fig. 9
figure 9

Hydraulic fracturing height for case 2 at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image

In Fig. 9, the fracture propagates firstly into the upper bedding at time step 40 (Fig. 9c) and then continues to develop into the upper bedding when the time passes (Fig. 9d). This observation yields well with the results in case 1 because when Young’s modulus of the reservoir is higher than Young’s modulus of the bedding, the fracture can develop into the bedding. This observation indicates that the fracture can develop more easily in the zone with a lower Young’s modulus than in the zone with a higher Young’s modulus, which can logically be explained by the fact that Young’s modulus is normally proportional to the fracture toughness (Kobayashi 2004). Hence, when Young’s modulus increases, the fracture toughness increases also and therefore the propagation of the fracture will be more difficult. The results obtained so far demonstrate the importance of knowing the character of the zones, not only the ones of the reservoir but also of the adjacent layers. The more accurate the values of Young’s modulus of this zone are, the more accurate the prediction of hydraulic fracture height is.

Impact of the Poisson ratio on the hydraulic fracture height

To study the impact of Poisson ratio on the hydraulic fracture height, we distinguish the Poisson ratio values of the reservoir and of the upper and lower barriers. In case 3, we consider the same Poisson ratio values for the beddings (ν = 0.3) while varying the values of the formation from ν = 0.1 (lower than the beddings’ Poisson ratio) to ν = 0.25 (nearly equal to the beddings’ values) and finally to ν = 0.4 (higher than the beddings’ values). The simulation results for these different scenarios in case 3 are presented in Figs. 7, 10, and 11, respectively. It is noted that the scenario where the Poisson ratio of the reservoir equal to 0.25 is also the basic case 0, which explains why the results of this case are already presented in Fig. 7.

Fig. 10
figure 10

Hydraulic fracturing height for case 3a at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image
Fig. 11
figure 11

Hydraulic fracturing height for case 3c at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image

To facilitate the analysis of the results, Fig. 12 presents the summary of the development of fracture height of case 3 in function of time. The results are surprising because it is expected to have differences in the development of the fracture height for different values of Poisson ratio. As it is well known that the Poisson ratio is related to the Young’s modulus (Eq. 38), the results from the previous section might give prediction that when Poisson ratio varies, the fracture height varies as well.

$$E \, = \, 2G \cdot (1 + \nu )$$
(38)
Fig. 12
figure 12

Development of fracture height for different values of reservoir’s Poisson ratio

Full size image

with E is Young’s modulus, G is the shear modulus, and ν is the Poisson ratio.

Another reason is that the lower the Poisson ratio is, the more brittle the rock is, and the higher the Poisson ratio is, the more ductile the rock is Cao and Li (2016). However, the results indicated that although some minor differences can be observed at the initial stage, the fracture height of all scenarios will be the same when more time passes. It is concluded that the impact of the Poisson ratio is very small and can be considered insignificant when being compared with the impact of Young’s modulus. Figure 12 clearly shows that the fracture height is greater than the reservoir thickness, independently of the reservoir’s Poisson ratio. This remark yields well with the results from the previous section which showed that when Young’s modulus of the reservoir is higher than Young’s modulus of the beddings, the fracture would propagate into the beddings. The conclusion that can be deducted from the results of case 3 is that the effect of Young’s modulus on hydraulic fracture height overwhelms the effect of the Poisson ratio.

Impact of the maximum horizontal principal stress on the hydraulic fracture height

The impact of the stress state underground was studied in case 4 where the maximum horizontal principal stress (Shmax) in the reservoir varies from 20 MPa (case 4a) to 25 MPa (case 4b), and then to 40 MPa (case 4c). The results of these cases are, respectively, presented in Figs. 7, 13, and 14. The first remark that can be deduced from these results is that when the Shmax of the reservoir increases, the fracture’s width decreases. The same observation can be obtained for the fracture height (Fig. 15). These observations can be explained by the following explication: when Shmax increases, the pressure caused by the injection fluid must firstly be higher than the compression stress underground in order to crack the rock; hence, the higher the Shmax is, the higher the injection fluid’s pressure must be to maintain the same fracture height. However, as the injection fluid’s flow rate is maintained the same at 0.01 m3/s, the pressure is practically the same for all cases (Fig. 16), so when the Shmax increases, the fracture height, and width decrease. The following suggestion for the application of hydraulic fracturing, in reality, can be deduced from these results: if the hydraulic fracturing will be operated at different depths and we want to have the same fracture height, we need to increase the injection rate because in general, the higher the depth is, the higher the Shmax is.

Fig. 13
figure 13

Hydraulic fracturing height for case 4b at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image
Fig. 14
figure 14

Hydraulic fracturing height for case 4c at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, and d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image
Fig. 15
figure 15

Development of fracture height for different values of maximum horizontal principal stress in the reservoir

Full size image
Fig. 16
figure 16

Fracturing pressure in different cases

Full size image

Impact of the fracture energy on the hydraulic fracture height

In case 5, another mechanical property of formation rock, which is the fracture energy, is studied to find out how it impacts the hydraulic fracture height. Fracture energy is a material property, which is defined as the energy required to change a unit area of a fracture surface from its initial unloaded state to a state of complete separation. The fracture energy of the formation rock varied from 4000 to 8000 N/m, and then to 16,000 N/m. The fracture height simulation results are presented in Fig. 17. We actually expected to see a clear difference in fracture height between the cases. However, although we observed a decrease in fracture height when the rock’s fracture energy increases, the difference is small, especially at the later stages. A possible explanation here is that the fracture pressure used in the simulation is too high, therefore even if the fracture energy increases, that augmentation is still futile in comparison with the fracture pressure. As a result, only a slight difference can be observed in the results. In conclusion, it is not essential in reality to acquire the fracture energy of the rock to accurately estimate the fracture height. As fracture energy is not an easy parameter to determine, the results of this research allow a decrease in the number of tests before running a hydraulic fracturing job, and therefore the cost will be decreased.

Fig. 17
figure 17

Development of fracture height for different values of fracture energy of the formation rock

Full size image

Impact of the formation rock’s porosity on the hydraulic fracture height

In case 6, the effect of formation rock’s porosity on the hydraulic fracture height was studied by varying the porosity from 20% (basic case) to 8%. The result of this case 6 is presented in Fig. 18. For a reminder, the result of the basic case is presented in Fig. 7.

Fig. 18
figure 18

Hydraulic fracturing height in case 6, where the reservoir’s porosity is equal to 8%, at different times after the beginning of the fracturing process: a 10 steps, b 20 steps, c 40 steps, d 60 steps. One time step is 100 s. Pressure unit is Pa

Full size image

The comparison between Fig. 7 (basic case) and Fig. 18 (case 6) showed that the results are nearly the same in these two cases. This observation is very surprising at first view because we normally thought that the porosity is generally proportional to the permeability (although in reality, the permeability depends also on the tortuosity), hence it was expected to obtain a decrease in fracture height when the porosity decreases. However, the result indicated that the rock’s porosity did not clearly influence the fracture height. In order to explain this conclusion, we refer to the calculation of the leak-off coefficient given in Eq. 39 (Settari 2013):

$$c = \sqrt {\frac{{kC_{{\text{f}}} \phi }}{\pi \mu }} \Delta P$$
(39)

where c is the leak-off coefficient, m s−0.5, Cf is the fluid compression coefficient, 1/Pa; μ is the viscosity of fracturing fluid, Pa.s; k is the reservoir permeability, m2; ΔP is the pressure difference between a hydraulic fracture and rock matrix, Pa, ϕ is the porosity. The leak-off coefficient is an important factor in hydraulic fracture.

From Eq. 39, if the porosity varies from 20 to 8%, while supposing that others parameters stay constant, then the leak-off coefficient will decrease by a factor of 1.58. In comparison with the influence of the permeability, for example, if the permeability varies from 10–14 to 10–15 m2, then the leak-off coefficient will decrease by a factor of 3.1, which is much higher than 1.58. In case the permeability changes by a factor of more than 100 times, its effect on the leak-off coefficient will be much clearer. For these reasons mentioned above, it is understandable that the variation of formation’s porosity does not have a clear effect on the fracture height.

Conclusions

This paper conducted research about the impact of uncontrolled parameters in a hydraulic fracturing operation on the height of the hydraulic fracture. For this objective, a model was built using a cohesive zone method to simulate the hydraulic fracture. Then, a sensitivity study was carried out for the properties of the rock such as Young’s modulus, Poisson ratio, maximum horizontal principal stress, fracture energy, and porosity.

Firstly, the results showed that if the Young’s modulus of the reservoir is higher than the ones of adjacent layers, it is suggested that the hydraulic fracture will spread easily into the adjacent layers. As a result, water flooding or unwanted gas production can occur. Therefore, caution measures must be taken in this case in order to achieve optimum results in reality.

Secondly, although the Poisson ratio is related to Young’s modulus, the effect of Poisson ratio on fracture height is insignificant and its impact is overwhelmed by the one of Young’s modulus.

Regarding the maximum horizontal stress of the formation rock, if its value increases, the fracture’s width and height both decrease. Hence, if the hydraulic fracture takes place at different depths of the well, we should think about a way to effectively control the fracture height, for example, by varying the injection rate of the fracturing fluid.

The results of this research indicated that the fracture height can be influenced by the formation rock’s fracture energy, although this influence is small. The advantage of this result is that it allows engineers to decrease the cost used for testing the rock’s fracture energy. However, this conclusion must be used with care in the future, because it might be that the high fracture pressure used in this research dominated the influence of fracture energy of the rock.

Last but not least, the effect of formation rock’s porosity on the fracture height was not clearly observed. However, the role of porosity is important because it can be used to estimate other parameters more accurately such as the permeability and the leak-off coefficients, which can be used for the modeling of the development of hydraulic fracture geometry.