Introduction

The drilling window refers to the range of fluid gradients between the pore and fracture pressure gradients in the drilling design, with the aim of maintaining the formation pressure after opening it (Huque et al. 2020). In conventional drilling, to prevent any formation influx, a wider drilling window is one of the prerequisites for the slightly overbalanced drilling technology. However, it is difficult to establish the formation pore pressure during drilling for the carbonated formation with well-developed fractures and caves. Therefore, the conventional drilling method is no longer applicable to carbonated formation due to a relatively narrow drilling window. A mud weight slightly lower than the formation pore pressure could result in formation influx or blowouts. However, a mud weight slightly higher than the formation pore pressure could cause lost circulation, which could induce reservoir contamination (McMillan et al. 2010). These problems exert an adverse influence on the control of wells. The mud loss and formation influx often occur in drilling operations, which would dramatically increase the non-productive time (NPT) and impair the project economics and reservoir recovery. In addition, improper handling may cause serious uncontrolled blowouts, thus posing a huge threat to workers’ safety and environmental protection.

It remains unclear about the overflow mechanism of such complex formations as carbonate formation, which causes a hindrance to the prevention and treatment of overflow. In recent years, many researchers have conducted various studies on the overflow mechanism of fractured formations. These studies can mainly be divided into three forms, including experimental analysis, analytical/mathematical model, and numerical simulations. A brief overview of several notable works in each form is provided as follows.

Firstly, the experimental analysis of gas kicks has attracted much attention from researchers. For instance, Johnson and Cooper (1993) conducted gas kick rise tests in a realistic drilling geometry with theologically accurate fluids. They conducted a test with both a 7.8 in. pipe and a 7.8ʺ × 3.25ʺ eccentric annulus. They found that there were differences in the effects of deviation between the pipe and the annulus. Further, they concluded that there was a significant effect of deviation on the rise velocity of gas in a well. Johnson and White (1993) continued their experiments with non-Newtonian fluids and reported that gas migration velocity would be larger in viscous fluids than in the air–water flow.

Marques et al. (2018), conducted olefin experiments to obtain a more thorough understanding of one special synthetic-based drilling fluid. They measured the PVT characteristics of olefin/methane mixtures. Further, they summarized the effects of temperature and pressure on thermodynamic properties.

Kaldirim and Schubert (2017, 2018) used a clear PVC pipe with a size of 27 feet and 6 in to simulate a CML Drilling Riser Model. Besides, an inner PVC pipe with a diameter of 2 in was used to circulate drilling fluid through the system. By increasing the mudflow rate, the phenomenon that a single Taylor bubble kick dispersed into a regional bubbly flow was observed. Furthermore, they reported that when the pressure at the top was reduced to 1.95 Pisa, the gas bubble was expanded during its migration in the PVC pipe to minimize the height limitations of their flow loop.

Fransolet et al. (2005), conducted gas–liquid two-phase flow experiments. In their efforts, two experimental methods (ERT and parietal pressure probes) were used to determine the average gas holdup. They reported that there were differences in the gas flow patterns between Newtonian fluids and non-Newtonian fluids.

Qureshi et al. (2019), conducted solid–liquid-gas three-phase experiments in the horizontal flow loop. The electrical resistance tomography (ERT) system was used to determine the volume fraction. It was observed that the ERT system played an important role in determining the volume fraction of the secondary phase (solid and air). It was inferred from the experimental results that the concentration of the secondary phase (solid and air) was affected by changes in the eccentricity of the inner pipe. Moreover, the inner pipe rotation exerted no significant influence on the concentration. Although the ERT system is recognized as one of the optimal tools for the observation of G–L flow, its application in monitoring the gas influx is still limited.

Secondly, the mathematical modeling of gas kick problems has also been conducted by some researchers. Velmurugan et al. (2016), established some mathematical models to explore various dynamic parameters of gas expansion in marine risers with mathematical analysis methods. Matlab was used to calculate the "Riser Equilibrium Point" under the assumption of the isolated riser with contaminated mud. They employed the correlations developed by Vasquez and Beggs (1980) to estimate the expansion in the drilling fluid. They also utilized the correlations developed by O’Bryan et al. (1988) and Thomas et al. (1984), to calculate gas solubility and bubble point, respectively.

Manikonda et al. (2019) established a semi-analytical model to simulate various gas kicks in an annulus under different conditions. A drift-flux model was adopted to simulate the gas behavior. The results showed that bubble rises velocity closely correlated with the drilling fluid circulation speed. The Peng-Robinson equation of state (EOS) and van der Waals mixing rules were used to account for gas solubility in mud. They also used the equations proposed by Hasan and Kabir (1992) to explain Taylor bubble rise velocity in an annulus. Their temperature modeling can be improved not only by a linear profile but also by heat transfer.

Finally, the numerical simulation of gas kick problems has also been performed by several researchers. Karimi Vajargah and van Oort (2015) developed a fast and accurate decision-making method, which could be used to automatically select the optimal well control response. Their numerical simulator combined a transient multi-phase flow model based on mass and momentum conservation. They compared the actual well response with the simulation results during an influx. Besides, they identified the optimal response with the assistance of a proposed algorithm (Yu et al. 2013). Karimi (2015) expounded an automated decision-making flowchart for well control during managed pressure drilling (MPD) operations.

However, there are still some deficiencies in the above-mentioned studies. For example, only the fractures under a constant pressure boundary are considered in the study with CFD simulation and the simplified model of the gravity displacement gas kick, and the closed boundary is not included. Additionally, the influence of fracture shape, fracture inclination, degree of wellbore penetration of fractures, construction conditions, and other factors on the gravity displacement gas kick is also ignored. In view of the above shortcomings, a simplified model of the gravity displacement gas kick in fractured carbonate formation was established in this study. Besides, the model was also verified and the influencing factors were analyzed.

There are differences in the pressure gradient between the drilling fluid inside the wellbore and the formation fluid outside the wellbore. Thus, the drilling fluid will enter the formation from the bottom of the fractures or karst caves, and the laminar ground flow will be displaced from the top of the fracture or karst caves (Zhi 2008; Shunhui 2015; Jun et al. 2018; Liujie 2017; Gang 2012; Hongjun et al. 2010; Xingquan et al. 2014; Cuny 2015). The difference between the two pressure gradients caused by the difference in density would cause a gravity displacement gas kick (Zongjin 2004). It commonly occurs under the conditions that there are different fluid pressure gradients on both sides of the wellbore and that pressures equal to the absolute value at one point, otherwise only the overflow or only loss. In terms of the constant pressure boundary fractures, the gas reservoir is supplied at the edge of the fracture, and the gas reservoir pressure remains unchanged. If a gravity displacement gas kick occurs, the pressure at a point in the fracture is equal to the fluid column pressure of the corresponding wellbore drilling fluid. In terms of the closed boundary fractures, the gravity displacement gas kick is bound to occur. Therefore, the fracture boundary type can be judged by imaging logging analysis and adjacent wells' drilling data in practical drilling. If the formation fracture size is large, the connectivity is good, and the gas source supply is sufficient, it will be determined as a constant pressure boundary fracture. Similarly, if the formation fracture connectivity is poor and there is no external pressure, it will be determined as a closed boundary fracture. According to the actual drilling situations and the theoretical analysis of gravity displacement, the conditions for gravity displacement gas kick are presented as follows (Xingquan et al. 2015). (1) There is a fracture channel with good spatial connectivity; (2) The fracture has a specific longitudinal extension; (3) The fracture has enough space.

CFD simulation of the gravity displacement gas kick in a fractured formation

In this study, ANSYS Fluent was used to simulate the gravity displacement gas kick, and geometric models of two types of boundary fractures were established (Fig. 1). The wellbore and fracture space were simulated by cylinders, and the formation fracture was simulated by plates. The diameter and height of the cylinder are 0.1 m and 0.6 m, respectively. The length and height of the flat seam are 0.4 m and 0.5 m, respectively. The hexahedral mesh was used to divide the 3D geometric model to ensure that each mesh was in the shape of a hexahedron, which reduced the calculation amount and improved the calculation accuracy. The VOF module in the software was used to conduct calculations, and the whole calculation process was transient calculation. The gravity displacement gas kick under the constant pressure boundary and closed boundary were simulated under average temperature and pressure.

Fig. 1
figure 1

CFD geometrical model of gravity displacement

Full size image

The dynamic laws of the gravity displacement gas kick under a constant pressure boundary

The fracture space was initially filled with gas, and the fracture pressure was 3.5 kPa. The wellbore was filled with drilling fluid, and the wellbore bottom pressure was 7.0 kPa. The fracture width was 2 mm, and the gas density and viscosity were 1.25 kg/m3 and 0.1 mPa s, respectively. The drilling fluid density and viscosity were 1200 kg/m3 and 5 mPa s, respectively. ANSYS Fluent was used to conduct a simulation, and the dynamic laws of the gravity displacement gas kick under a constant pressure boundary fracture were obtained (Figs. 2, 3, 4).

Fig. 2
figure 2

Two-phase dynamic law of gravity displacement under a constant pressure boundary

Full size image
Fig. 3
figure 3

Velocity vector nephogram of gravity displacement under a constant pressure boundary (t = 4.9 s)

Full size image
Fig. 4
figure 4

Pressure nephogram of gravity displacement under a constant pressure boundary (t = 4.9 s)

Full size image

Figure 2 shows the dynamic laws of the gravity displacement gas kick under a constant pressure boundary fracture with a penetration of 0.5 m. As shown in the figure, the gas begins to move to the wellbore's upper end at the initial moment due to the density difference, and the drilling fluid at the wellbore's bottom flows to the fracture due to gravity. The angle between the gas–liquid interface and the horizontal surface decreases with the increase of time. At 0.24 s, the bottom drilling fluid almost invades the right end of the fracture, and the gas at the top end of the fracture flows out through the wellbore. Subsequently, the drilling fluid flowing through the fracture enters the right fracture space and flows out of the lower part of the right fracture space under the action of gravity. It can be seen that the whole process tends to be stable at about 1 s. Hence, the gravity displacement gas kick under the constant pressure boundary fracture can be regarded as a steady-state process.

Figure 3 shows the velocity vector nephogram of the gravity displacement gas kick under a constant pressure boundary fracture under stable conditions. As shown in the figure, the gas velocity is much higher than the drilling fluid velocity, and the gas on the right side gradually flows to the left and upper sides, which causes a large gas outlet velocity on the upper left side. The liquid velocity also presents a similar phenomenon, but it is not apparent due to a small flow velocity. The velocity in the fracture space on the right side is slightly higher than that in the wellbore on the left side. This phenomenon is caused by the fact that the pressure in the fracture space is maintained by the significant gas flow rate and the inflow of gas under a constant pressure boundary on the upper end (Fig. 4). As shown in the pressure nephogram, the pressure on the left wellbore is almost hydrostatically distributed, the pressure in the fracture space on the right maintains at 3.5 kPa, and there is a gradual transition for the pressure distribution in the middle fracture area.

The dynamic laws of the gravity displacement gas kick under a closed boundary

The primary data of a closed fracture simulation were the same as those of a constant pressure fracture simulation. The dynamic laws of the gravity displacement gas kick under a closed boundary fracture were obtained (Figs. 5, 6, 7).

Fig. 5
figure 5

Two-phase dynamic law of gravity displacement under a closed boundary

Full size image
Fig. 6
figure 6

Velocity vector nephogram of gravity displacement under a closed boundary (t = 10 s)

Full size image
Fig. 7
figure 7

Pressure nephogram of gravity displacement under a closed boundary (t = 10 s)

Full size image

Figure 5 shows the dynamic laws of the gravity displacement gas kick under a closed boundary fracture. As shown in the figure, the drilling fluid invades the right bottom of the fracture and begins to flow into the right fracture space at 0.22 s. It shows that the gas at the lower end of the fracture space on the right side migrates upward under the action of buoyancy and flows out from the upper end of the wellbore on the left side due to the closed fracture and the absence of external air supply. The gas in the entire fracture space on the right is decreasing due to the drilling fluid invasion. Eventually, the drilling fluid will completely displace the gas in the fracture space, and the gravity displacement gas kick comes to an end.

As is revealed from a comparative analysis of the gravity displacement gas kick law under the two boundaries, the overflow rate of a closed fracture is lower than that of a constant pressure fracture. This phenomenon is not conducive to timely detection of overflow, which increases the risk of the well out of control. As can be seen from the red area at the left upper end of the wellbore in Figs. 2 and  5, the red area of constant pressure fractures is more extensive, which would disturb the wellbore drilling fluid. The red area of closed fractures is close to that of the wall of the wellbore.

As shown in Fig. 6, the outlet velocity at the upper left end of the fracture is much smaller than that of the constant pressure boundary fracture. For the reason that there is no continuous supply of external energy to the closed fracture, the gas flow rate at the right side of the fracture decreases continuously. Figure 7 shows that the pressure in the area occupied by gas in the right fracture space gradually decreases. After relevant calculations, the gravity displacement overflow rate under a closed boundary is almost equal to the leakage rate. This phenomenon is caused by the fact that although the gas pressure is reduced, the reduced amount can hardly cause the expansion of the gas. Meanwhile, the amount of drilling fluid leakage will match the gas overflow.

Simplified models of gravity displacement in a fractured formation

A simplified model of gravity displacement under a constant pressure boundary

When drilling into the fracture under a constant pressure boundary, the negative pressure gas kick may occur first. With the increase of the drilling depth, the bottom hole pressure gradually increases. When it increases to a value equal to the fracture pressure, leakage will occur, thus resulting in leakage in the lower section and overflow in the upper section (Liu Huixin and Li Feng 2011). If the penetration degree of the fractures remains unchanged, the gas–liquid replacement would become stable at this moment. That is to say, both the leakage rate and the gas invasion rate are constant. The assumptions related to the simplified model are elucidated as follows.

  • (1) The fracture height is a constant value, the width of the fracture is equal everywhere, and the gas–liquid flow satisfies the cubic law (Hajjar et al. 2018);

  • (2) There is a fracture under a constant pressure boundary;

  • (3) The drag between gas and liquid phases is not considered (Chen et al. 2004);

  • (4) The influence of temperature distribution on the gravity displacement gas kick is ignored.

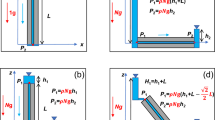
The wellbore passes through a high-angle fracture, and its section is elliptical. In the calculation, the ellipse is simplified as a rectangle. The angle between the wellbore axis and the fracture surface determines the fracture penetration length (H) (Fig. 8).

Fig. 8
figure 8

Schematic diagram of the wellbore penetrated fracture

Full size image

The simplified model is shown in Fig. 9. The gas–liquid interface is simplified to a straight line to simplify the calculation. The wellbore pressure corresponding to the height of the interface is equal to the gas reservoir pressure, and the liquid and gas flow rates near the gas–liquid interface are zero. Below the gas–liquid interface, the liquid velocity gradually increases with the increase of depth; Above the gas–liquid interface, the gas velocity gradually increases with the decrease of depth.

Fig. 9
figure 9

Schematic diagram of the gravity displacement gas kick under a constant pressure boundary

Full size image

When there is fluid flowing in the fracture, the fracture surface is in close contact with the liquid and will exert resistance. According to the fluid microelement force analysis, the wall's resistance to the fluid flowing forward is equal to the pressure difference between the fluid microelement's front and back under steady-state conditions. For gas and liquid:

$$\tau_{{{\text{wg}}}} (y) = \frac{{6{\mu v}_{{\text{g}}} (y)}}{b}$$
(1)
$$\tau_{{{\text{wl}}}} (y) = K\left( {4 + \frac{2}{n}} \right)^{n} \left( {\frac{{v_{l} (y)}}{b}} \right)^{n} .$$
(2)

The resistance of the drilling fluid flowing from the wellbore to the gas reservoir is equal to the pressure difference:

$$\frac{{2\tau_{{{\text{wl}}}} (y)h_{f} }}{{b\rho_{l} {\text{g}}}} = \left[ {p_{l} (y) - p_{{\text{g}}} (y)} \right]\sin \theta .$$
(3)

The resistance of the natural gas flowing from the gas reservoir to the wellbore is equal to the pressure difference:

$$\frac{{2\tau_{{{\text{wg}}}} (y)h_{f} }}{{b\rho_{g} {\text{g}}}} = \left[ {p_{{\text{g}}} (y) - p_{l} (y)} \right]\sin \theta$$
(4)
$$q_{{\text{l}}} = \int {2h_{l} {\text{bv}}_{l} (y)} {\text{dy}}$$
(5)
$$q_{{\text{g}}} = \int {2h_{{\text{g}}} {\text{bv}}_{{\text{g}}} (y)} {\text{dy}}{.}$$
(6)

The leakage rate and overflow rate can be calculated based on Eqs. (3)–(6).

A simplified model of gravity displacement under a closed boundary

The constant pressure boundary fracture does not exist in the natural formation. After the gas continues to flow out, the pressure outside the fracture will gradually decrease. In terms of the closed fractures without pressure supply, the loss of gas in the fracture or the filling of external drilling fluid will affect the fracture pressure, thereby affecting overflow and leakage.

When drilling into the fracture under a closed boundary, overflow or leakage often occurs first. When the overflow or leakage continues to develop, the pressure of the fracture gradually decreases or increases to a value equal to the wellbore pressure, and gravity displacement will occur at this time. It should be noted that the occurrence of the gravity displacement gas kick is irrelevant to the fracture penetration length and the initial fracture pressure (Xiangyang et al. 2018; Guoping et al. 2018; Xiangwei et al. 2015). The process of gravity displacement caused by drilling into high-pressure fractures is analyzed, with the physical model shown in Fig. 10. The assumptions related to the simplified model are elucidated as follows.

  • (1) The fracture height and length are fixed values, the width of the fracture is equal everywhere, and the gas–liquid flow satisfies the cubic law;

  • (2) There is a fracture under a closed boundary, and there is no external gas supply;

  • (3) The lost drilling fluid is deposited on the lower end of the fracture;

  • (4) The drag between gas and liquid phases is not considered;

  • (5) The influence of temperature distribution on the gravity displacement gas kick is ignored.

Fig. 10
figure 10

Schematic diagram of the gravity displacement gas kick under a closed boundary

Full size image

Gas invasion occurs in the upper section of the wellbore profile, and drilling fluid loss occurs in the lower area. The length of the gas invasion section and the leakage section is determined by the fracture pressure (Yong et al. 2019; Jun et al. 2019):

$$h_{l} (t) = \frac{{p_{{\text{g}}} (0) - p_{{\text{g}}} (t)}}{{\rho_{l} {\text{g}}\sin \theta }}$$
(7)
$$h_{{\text{g}}} (t) = h - h_{l} (t).$$
(8)

The amount of natural gas in the fracture will be affected by the gas overflow:

$$N(t) = \frac{{p_{{\text{g}}} (0)l_{1} l_{2} b}}{{z(0){\text{RT}}}} - \frac{{p_{g} (t)\int {Q_{{\text{g}}} (t)} {\text{dt}}}}{{z(t){\text{RT}}}}.$$
(9)

The drilling fluid entering the fracture will affect the space occupied by natural gas:

$$V_{{\text{g}}} (t) = l_{1} l_{2} b - \int {Q_{l} (t)} {\text{dt}}{.}$$
(10)

The amount of drilling fluid loss and natural gas invasion at a specific moment can be calculated based on Eqs. (7)–(10), followed by the calculation of the fracture pressure at the next moment.

Verification of the simplified gravity displacement gas kick model

In this study, the simplified model was established to calculate the overflow rate and the leakage rate under specific working conditions. In actual drilling, fracture opening and drilling fluid density (wellhead backpressure) are two parameters with the most significant influence on gravity displacement. Therefore, the simplified model was verified with these two influencing parameters. Besides, the simplified model results and CFD simulation results related to these two parameters were compared under a constant pressure boundary.

Fracture opening

The primary data for relevant simulation and calculation are presented as follows. The lengths of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures are both 0.25 m. The fracture length is 0.5 m. The fracture inclination is 90°. The drilling fluid density is 1.2 g/cm3. The drilling fluid consistency coefficient and fluidity index are 0.4 Pa sn and 0.4, respectively. The leakage rate and overflow rate are calculated when the fracture opening is 1 mm, 2 mm, 3 mm, and 4 mm, respectively. The steady-state velocity vector diagram (Fig. 11) is obtained by CFD simulation. The exported data are accumulated and then compared with the simplified model results (Fig. 12).

Fig. 11
figure 11

Steady-state velocity vector diagram of gravity displacement under a constant pressure boundary with different fracture opening diameters (t = 10 s)

Full size image
Fig. 12
figure 12

Comparison of the calculation results of the leakage rate and overflowrate under different fracture opening diameters

Full size image

Drilling fluid density

The primary data for relevant simulation and calculation are presented as follows. The lengths of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures are both 0.25 m. The fracture length is 0.5 m. The fracture inclination is 90°. The fracture opening is 2 mm. The drilling fluid consistency coefficient and fluidity index are 0.4 Pa sn and 0.4, respectively. The leakage rate and overflow rate are calculated when the drilling fluid density is 1.0 g/cm3, 1.2 g/cm3, 1.3 g/cm3, 1.4 g/cm3, respectively. The steady-state velocity vector diagram (Fig. 13) is obtained by CFD simulation. The exported data are accumulated and then compared with the simplified model results (Fig. 14).

Fig. 13
figure 13

Steady-state velocity vector diagram of gravity displacement under a constant pressure boundary with different drilling fluid densities (t = 10 s)

Full size image
Fig. 14
figure 14

Comparison of the calculation results of the leakage rate and overflow rate under different drilling fluid densities

Full size image

As shown in Figs. 12 and 14, the changing trend of the calculated results based on the simplified model is consistent with that based on CFD simulation. There is a more significant changing trend for the former compared with the latter. This phenomenon is caused by the fact that the gas-liquid interface is regarded as a horizontal plane in the simplified model. Moreover, more factors (such as interfacial tension) are included in the calculation of CFD simulation, which also contributes to a more significant changing trend for the results of the simplified model. The maximum comparison error of the calculation example is 33%. In the absence of experimental and field data, the results calculated based on the simplified model can be used as approximate values of the actual condition.

Analysis of influencing factors of the gravity displacement gas kick

Based on the above steady-state model and transient model, the influence of the fracture opening, fracture inclination, drilling fluid rheological parameters, fracture penetration length, wellhead backpressure, fracture length, and drilling fluid density on the replacement rate (leakage rate and overflow rate) of the fractures under two boundary conditions were explored, respectively. Standard parameters involved in the calculation are presented as follows. The formation temperature is 39 K. The fracture depth is 4247 m. The initial fracture pressure is 50 MPa. The fracture height is 30 m. The wellbore diameter is 0.15 m.

Fracture opening

The primary data for relevant calculations are presented as follows. The length of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures is 0.8 m and 0.2 m, respectively. The penetration length of the closed boundary fracture is 1.0 m. The fracture length is 50 m. The fracture inclination is 90°. The drilling fluid density is 1.2 g/cm3. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. Based on these data, the leakage rate and overflow rate of constant pressure boundary fractures are calculated when the fracture opening is 0.5 mm, 1.0 mm, 1.5 mm, 2.0 mm, 2.5 mm, and 3.0 mm, respectively (Fig. 15). Besides, the displacement rate of the closed boundary fractures is calculated when the fracture opening is 1.5 mm, 2.0 mm, 2.5 mm, and 3.0 mm, respectively (Fig. 16).

Fig. 15
figure 15

Changes in the leakage rate and overflow rate with fracture opening under a constant pressure boundary

Full size image
Fig. 16
figure 16

Changes in the displacement rate with fracture opening under a closed boundary

Full size image

As is revealed from relevant calculation results, the leakage rate and overflow rate of the closed boundary fracture are the same. This phenomenon is caused by the fact that the fracture pressure remains almost unchanged in the gravity replacement process, and hence the volume of natural gas in the fracture hardly changes. Therefore, macroscopically, the volume of drilling fluid leaking into the fractures is basically the same as that of natural gas flowing into the wellbore, which can be expressed as the "replacement rate".

As shown in Fig. 15, the leakage rate and overflow rate increase exponentially with the increase of the fracture opening. The phenomenon is caused by the fact that the larger the fracture opening, the larger the equivalent permeability, and the smaller the fluid flow resistance. Besides, the flow rate of drilling fluid and natural gas increases, and the flow channels also get more extensive, which together results in the exponential increase of the flow rate of natural gas and drilling fluid. Simultaneously, it should be noted that when there is an equal pressure difference, the overflow rate of the constant pressure boundary fracture is much larger than the leakage rate, for the reason that the viscosity of natural gas is much smaller than that of drilling fluid. As shown in Fig. 16, the larger the fracture opening, the more gas in the fracture, but the shorter the replacement duration. It indicates that fracture opening exerts a significant influence on the replacement rate. When the fracture opening is 3 mm, the replacement rate could reach 1.1 m3/h, which may cause safety hazards.

Figure 16 shows that the gravity displacement rate of the closed fracture gradually increases with time. This change is specifically manifested as a slight increase during the early stage and a significant increase during the later stage. The end of the curve indicates the end of the gravity displacement overflow. The fracture is filled with drilling fluid, and the slope of the curve is getting larger. The phenomenon is caused by the fact that the smaller the volume of gas in the fracture, the smaller the gas space in the fracture, the more significant the influence of the same amount of drilling fluid entering the fracture on the pressure, the more apparent the fracture pressure fluctuations, and the faster the replacement rate. Therefore, it is required to effectively eliminate the gravity replacement overflow in case of its occurrence. Otherwise, the replacement rate will become increasingly faster.

Fracture inclination

High-angle fractures occur in carbonate formations. However, there are few complete vertical fractures. Therefore, it is necessary to explore the influence of high-steep fractures and oblique fractures on gravity displacement.

The primary data for relevant calculations are presented as follows. The length of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures is 0.8 m and 0.2 m, respectively. The closed penetration length of the boundary fracture is 1.0 m. The fracture length is 50 m. The drilling fluid density is 1.2 g/cm3. The fracture opening is 2 mm. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. Based on these data, the leakage rate and overflow rate of constant pressure boundary fractures are calculated when the fracture inclination is 15°, 30°, 45°, 60°, 75°, and 90°, respectively (Fig. 17). Besides, the displacement rate of closed boundary fractures is calculated when the fracture inclination is 30°, 45°, 60°, and 90°, respectively (Fig. 18).

Fig. 17
figure 17

Changes in the leakage rate and overflow rate with the fracture inclination under a constant pressure boundary

Full size image
Fig. 18
figure 18

Changes in the displacement rate with the fracture inclination under a closed boundary

Full size image

As shown in Fig. 17, the leakage rate and overflow rate increase with the increase of the fracture inclination. However, the degree of this increase is getting smaller, showing a trend similar to a sine function. The larger the fracture inclination, the higher the pressure gradient corresponding to the wellbore, the more significant the difference between the fracture pressure and the larger the leakage rate and overflow rate. As shown in Fig. 18, the gravity replacement rate of a fracture with an inclination angle of 90° is almost three times that with an inclination angle of 30°. Therefore, the fracture inclination exerts a more significant influence on the replacement rate.

Drilling fluid rheological parameters

The primary data for relevant calculations are presented as follows. The length of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures is 0.8 m and 0.2 m, respectively. The drilling fluid density is 1.2 g/cm3. The fracture opening is 2 mm. The fracture inclination is 90°. The influence of the drilling fluid consistency coefficient and fluidity index on the leakage rate of constant pressure boundary fractures are analyzed based on the calculation results (Fig. 19).

Fig. 19
figure 19

The rate of leakage varies with the rheological parameter at constant pressure boundary

Full size image

As shown in Fig. 19, the larger the consistency coefficient and fluidity index, the smaller the drilling fluid leakage rate. Both present an exponential decrease trend. This phenomenon is caused by the fact that the consistency coefficient and fluidity index reflect the drilling fluid viscosity. Specifically, the more significant the viscosity, the larger the frictional resistance of the flow, the more difficult it is for the drilling fluid to flow into the fracture, and the lower the leakage rate. When the consistency coefficient and the fluidity index are larger than 1.0 Pa sn and 0.6, respectively, the drilling fluid loss rate can be controlled within 0.1 m3/h. The gravity displacement is not apparent, which would have little influence on safety production. Therefore, during on-site construction, the increase in the viscosity of the drilling fluid contributes to reducing the drilling fluid leakage rate, thereby inhibiting or avoiding the occurrence of gravity displacement.

Fracture penetration length

In the actual drilling process, the fracture penetration length is related to the angle between the wellbore axis and the fracture plane. Different fracture penetration lengths will exert different impacts on the gravity displacement rate.

The primary data for relevant calculations are presented as follows. The drilling fluid density is 1.2 g/cm3. The fracture opening is 2 mm. The fracture inclination is 90°. The fracture length is 50 m. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. Based on these data, the leakage rate is calculated when the leakage channel length of the constant pressure boundary fracture is 0.8 m, 1.0 m, 1.2 m, 1.4 m, and 1.6 m, respectively. Besides, the overflow rate is also calculated when the overflow channel length is 0.2 m, 0.3 m, 0.4 m, 0.5 m, and 0.6 m, respectively (Fig. 20). In addition, the displacement rate of closed boundary fractures is calculated when the fracture penetration length is 1.0 m, 1.5 m, 2.0 m, and 2.5 m respectively (Fig. 21).

Fig. 20
figure 20

Changes in the leakage rate and overflow rate with the channel length under a constant pressure boundary

Full size image
Fig. 21
figure 21

Changes in the displacement rate with the fracture penetrating length under a closed boundary

Full size image

As shown in Fig. 20, the leakage rate and overflow rate of the constant pressure boundary fracture increase with the increase of the leakage channel length and overflow channel length. Further, the degree of this increase is getting larger. This phenomenon is caused by the fact that there are larger differences between the wellbore pressure and the fracture pressure corresponding to the newly added channel. As shown in Fig. 21, the initial replacement rate increases approximately linearly with the fracture penetration length. With the extension of the gravity displacement overflow time, the replacement rate increment corresponding to the same time point increases with the fracture penetration length. Therefore, it is required to make an attempt to avoid penetrating the fracture along the fracture extension direction.

Wellhead back pressure (drilling fluid density)

A certain bottom hole pressure can be maintained by adjusting the drilling fluid column pressure or using low-density drilling fluid under the premise that the wellhead backpressure is applied. The latter is the basic idea of the controlled pressure drilling technology, which has been used more frequently in the drilling of fractured carbonate formations. It has the advantage of achieving the real-time matching of the bottom hole pressure and the formation pressure by applying variable wellhead backpressure. During the development of the gravity displacement gas kick, the displacement rate will change when different wellhead backpressures are applied under the condition that the bottom hole pressure is a constant.

The primary data for relevant calculations are presented as follows. The length of the drilling fluid leakage section and gas invasion section of the constant pressure boundary fractures is 0.8 m and 0.2 m, respectively. The penetration length of the closed boundary fracture is 1.0 m. The fracture length is 50 m. The fracture opening is 2 mm. The fracture inclination is 90°. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. Based on these data, the leakage rate and overflow rate of constant pressure boundary fractures are calculated (Fig. 22). Besides, the displacement rate of closed boundary fractures (Fig. 23) is calculated when the wellhead backpressure is 0 MPa, 3 MPa, 6 MPa, 9 MPa, and 12 MPa, respectively (corresponding to the drilling fluid density of 1.20 g/cm3, 1.13 g/cm3, 1.06 g/cm3, 0.98 g/cm3, and 0.91 g/cm3).

Fig. 22
figure 22

Changes in the leakage rate and overflow rate with the wellhead backpressure under a constant pressure boundary

Full size image
Fig. 23
figure 23

Changes in the displacement rate with the wellhead backpressure under the closed boundary

Full size image

The wellhead backpressure is applied while ensuring that the bottom hole pressure remains unchanged. It indicates that the larger the backpressure, the lower the drilling fluid density. As shown in Fig. 22, the leakage rate and overflow rate decrease linearly with the increase of the wellhead backpressure, and the wellhead backpressure increases. Besides, the bottom hole pressure remains unchanged, the drilling fluid density decreases, and the wellbore pressure gradient decreases. When the difference with the fracture pressure decreases, the leakage rate and overflow rate decrease. As shown in Fig. 23, when the wellhead backpressure is not applied, the replacement rate is 0.35 m3/h. After the wellhead backpressure of 12 MPa is applied, the replacement rate drops to 0.22 m3/h, which effectively alleviates the gravity replacement. Therefore, the drilling method with low-density drilling fluid and wellhead backpressure may generate smaller gravity displacement compared with that with high-density drilling fluid. It is necessary to identify the optimal value of the wellhead backpressure based on specific drilling situations. For example, as per the above analysis results, the wellhead backpressure of 12 MPa can achieve optimal performance in alleviating the gravity displacement.

Fracture length

The primary data for relevant calculations are presented as follows. The penetration length of the closed boundary fracture is 1.0 m. The drilling fluid density is 1.2 g/cm3. The fracture opening is 2 mm. The fracture inclination is 90°. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. Based on these data, the displacement rate of closed boundary fractures is calculated when the fracture length is 30 m, 40 m, 50 m, and 60 m, respectively (Fig. 24).

Fig. 24
figure 24

Changes in the displacement rate with the fracture length under a closed boundary

Full size image

As shown in Fig. 24, the replacement rate decreases with the linear increase of the fracture length. The degree of this decrease is getting smaller. This phenomenon is caused by the fact that the longer the fracture length, the larger the fracture space. The process of an equal amount of drilling fluid entering the fracture or gas flowing out of the fracture has less influence on the fracture pressure, and hence the replacement at the next moment is smaller. Simultaneously, the longer the fracture length, the longer the duration of the gravity displacement gas kick.

Drilling fluid density

During the drilling in permeable siltstone formations, conventional well-killing methods are commonly used to treat the overflow in this process. The drilling fluid density would be increased during the application of this conventional method. However, fractures may occur in the fractured carbonate formations, and hence the overflow in this drilling process cannot be effectively controlled by increasing the drilling fluid density, which may even aggravate the overflow.

The primary data for relevant calculations are presented as follows. The penetration length of the closed boundary fracture is 1.0 m. The initial drilling fluid density is 1.2 g/cm3. The fracture opening is 2 mm. The fracture inclination is 90°. The fracture length is 70 m. The drilling fluid consistency coefficient and fluidity index are 0.8 Pa sn and 0.6, respectively. After the occurrence of the gravity displacement gas kick, the gravity displacement is analyzed by increasing the drilling fluid density by 0.1 g/cm3, 0.2 g/cm3, and 0.3 g/cm3, respectively (Fig. 25).

Fig. 25
figure 25

The influence of increasing the drilling fluid density on the displacement rate after the occurrence of gravity displacement

Full size image

As shown in Fig. 25, the initial replacement rate is 0.28 m3/h before increasing the drilling fluid density. After the overflow continues for one hour, the drilling fluid density is increased to 1.3 g/cm3, and the replacement rate increases to 0.32 m3/h. After the drilling fluid density is increased to 1.4 g/cm3, the replacement rate increases to 0.36 m3/h. After the drilling fluid density is increased to 1.5 g/cm3, the replacement rate increases to 0.40 m3/h.

This phenomenon can be explained as follows. After the drilling fluid density increases, the bottom hole pressure increases, and the bottom hole is transformed from the gravity displacement gas kick into leakage. Compared with the pressure difference of the gravity displacement gas kick, the positive pressure difference of leakage at this time is huge. A large amount of drilling fluid leaks into the fractures quickly and occupies the fracture space. The fracture pressure is increased until it is equal to the bottom hole pressure, and the gravity displacement gas kick occurs again. At this moment, the drilling fluid density increases, and the wellbore pressure gradient and replacement rate increase accordingly. The mechanism of gravity displacement gas kick can explain the phenomenon that the more the drilling fluid density increases after the overflow in the carbonate formation, the more violent the overflow during the on-site construction process.

The severity of this phenomenon is also related to the fracture opening under the condition that other conditions remain unchanged. This situation is analyzed under the condition that the drilling fluid density is increased to 1.4 g/cm3 after one hour of gravity displacement gas kick under the fracture openings of 0.5 mm, 1.0 mm, 1.3 mm, and 1.5 mm, respectively (Fig. 26).

Fig. 26
figure 26

The influence of increasing the drilling fluid density on the displacement rate after the occurrence of gravity displacement under different fracture openings

Full size image

As shown in Fig. 26, the increments of the drilling fluid density are equal; while, the increments of the replacement rate corresponding to different fracture openings are not equal. The larger the fracture opening, the larger the increase in the replacement rate, and the more the formation presents the characteristics of a fractured formation. The fluctuation of the bottom hole pressure has a significant influence on overflow and leakage. Specifically, the smaller the fracture opening, the more the formation presents the characteristics of a permeable formation. The overflow rate is always lower before and after the drilling fluid density is increased. It indicates that the smaller the fracture opening, the weaker the formation pressure sensitivity. The larger the fracture opening, the stronger the formation pressure sensitivity. This finding further proves that there are pressure sensitivity characteristics in the fractured carbonate formation.

Conclusions

  1. (1)

    The gravity replacement gas kick under a constant pressure boundary will stabilize in a short period, which can be regarded as a steady-state flow. While the rate of the gravity replacement gas kick under a closed boundary is manifested as a function of time.

  2. (2)

    The comparison between the simplified model and CFD simulation results demonstrates that this simplified model has specific applicability.

  3. (3)

    When the fracture opening is 3 mm, the replacement rate reaches 1.1 m3/h. The gravity replacement rate of a fracture with an inclination angle of 90° is almost three times that with an inclination angle of 30°. When the consistency coefficient and the fluidity index are larger than 1.0 Pa sn and 0.6, respectively, the drilling fluid loss rate can be controlled within 0.1 m3/h. When the wellhead backpressure is not applied, the replacement rate is 0.35 m3/h; while, after the wellhead backpressure of 12 MPa is applied, the replacement rate drops to 0.22 m3/h. The method based on the low-density and high-viscosity drilling fluid and wellhead backpressure in field construction can effectively alleviate the gravity displacement gas kick.

  4. (4)

    In terms of the fractures under a closed boundary, the gravity displacement gas kick may be aggravated by increasing the drilling fluid density after its occurrence. The larger the increase of the drilling fluid density, the larger the fracture opening, and the more severe the gravity displacement.