A 2-D analytical solution to infinite conductivity fracture injection pressure transient analysis in non-Newtonian/Newtonian composite infinite reservoirs

Abstract

Two fluid regions are usually created during either water or polymer injection into an oil reservoir for enhanced oil recovery. The two fluid regions create a composite reservoir system that requires analytical solution that can be used to evaluate the injection performance. In this study, we present a 2-D solution for non-Newtonian fluid in the inner zone coupled with infinite boundary in the outer zone using power law model. The outer zone fluid can either be Newtonian or non-Newtonian. Moreover, the mathematical model is formulated such that either zone can be with non-Newtonian power law fluid or Newtonian fluid. The infinite conductivity fractured solution obtained was compared with the ones obtained using the radial line source solution that had already been developed in the literatures, and a perfect match was obtained. An application was made to three examples that have been presented in a previous work, and satisfactory results were obtained. The dimensionless pressure drops during the early linear flow regime for all values of flow indices are the same, but with deviation during radial flow regime.

Introduction

Injecting foreign immiscible fluid into a reservoir or porous media will create a composite feature within the reservoir. In the oil exploitation, polymer, water or waste slurry can be injected into a reservoir for the purpose of enhanced oil recovery or waste disposal. Monitoring the injected fluid’s front is therefore necessary. Lund and Ikoku (1981) presented a numerical radial model for a composite reservoir with non-Newtonian fluid in the inner region (Zone 1) and Newtonian fluid in the outer region (Zone 2). Martha and Ertekin (1983) presented a Numerical Simulation of a Power-Law Fluid Flow in a Vertically Fractured Reservoir with finite conductivity. Ertekin et al. (1987) also presented another numerical method with similar composite reservoir as in Lund and Ikoku, but used finite conductivity hydraulic fracture. Prior to Ertekin et al.’s work, Ikoku and Ramey (1979), and Odeh and Yang (1979) have presented radial analytical line source solutions for a non-Newtonian fluid flow in porous media using power law model. The two solutions are similar and essentially the same in analytical approach. Vongvuthipornchai and Raghavan (1987) presented a numerical method for evaluating infinite conductivity hydraulic fracture with non-Newtonian power law fluid flow in porous media. They observed that the dimensionless pressure drops during early linear flow regime are the same for all flow behavior indices. Raghavan and Chen (2017) also presented a new analytical line source solution for non-Newtonian fluid, which was used to compute the dimensionless pressure drop for infinite conductivity hydraulic fracture. The early linear flow is not present in the work of Raghavan and Chen (2017) as observed in the numerical work of Vongvuthipornchai and Raghavan (1987).

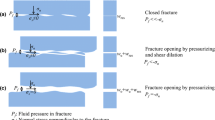
In this study, we developed a 2-D analytical solution for infinite conductivity hydraulic fracture in a composite reservoir with non-Newtonian fluid in the inner region (Zone 1) and Newtonian fluid in the outer region (Zone 2) as shown in Fig. 1. It is a general solution which can also be used for non-Newtonian fluid with different flow behavior index in Zone 1 and Zone 2. To the best of our knowledge, this analytical solution for a composite reservoir is appearing in the literature for the first time. Previous analytical works (such as Ambastha (1988) and, Abbaszadeh and Kamal (1989)) are on composite reservoir with Newtonian fluids in both Zone1 and Zone 2. van den Hoek et al. (2012) provided a method of analyzing pressure transient behavior in fractured polymer injection well. van den Hoek’s method of evaluation is to identify the non-Newtonian radial flow regime in the inner region (Zone 1) and fixed a straight line of the radial flow regime to estimate the flood front. van den Hoek et al. did not provide a matching in their field examples to capture the entire behavior of the pressure transient data.

Fig. 1

Reservoir conceptual model

We compared our 2-D analytical solution with the results obtained using Ikoku and Ramey (1979) and Odeh and Yang line source solutions to obtain infinite conductivity hydraulic fracture solution; we obtained a good match. However, our result is at variant with that of Raghavan and Chen (2017) when the flow behavior index is less than 1.0. We also used the 2-D solution we obtained, applying Cinco-Ley and Meng’s (1988) method to compute the dimensionless pressure drop for finite conductivity fracture and compared the results with that of Ertekin et al. (1987); we obtained a fairly perfect match that gave us confidence in our solution. van den Hoek et al. (2012) presented three field examples which practically demonstrated the problem we are addressing in this study. We used our 2-D model to match the pressure transient data and a good match was obtained. Thus, our 2-D model presented a new analytical method for analyzing fractured polymer or waste/drilling cuttings slurry injection well where two fluid zones are created due to the mobility and diffusivity ratios, and different flow behavior index in the two zones. Essentially, the major contribution of this study is the presentation of analytical solution that can be used to evaluate pressure behavior in a composite reservoir with two zones of different flow behavior index. It could be either non-Newtonian/Newtonian or non-Newtonian/non-Newtonian as the case may be. In Well Test Analysis, methods of estimating formation parameters are usually derived from the analytical solution.

The analytical solution in Laplace space is numerically converted to real-time space using Stehfest (1970) Algorithm 368.

Mathematical model

The linearized partial differential equation for naturally fractured reservoir (NFR) is

$${x}_{D}^{n-1}\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {x}_{D}^{2}} + {y}_{D}^{n-1}\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {y}_{D}^{2}}-sf\left(s\right)\overline{{P }_{Df}}=0$$

(1)

$$f\left(s\right)=\frac{\omega \left(1-\omega \right)s+\lambda }{(1-\omega )s+\lambda }$$

(2)

All the dimensionless variables and derivations are in “Appendix A”.

$$\omega =\frac{{(\varphi {c}_{t})}_{f}}{{(\varphi {c}_{t})}_{f}+{(\varphi {c}_{t})}_{m}}$$

(3)

$$\uplambda =\delta \frac{{k}_{m}{x}_{f}^{2}}{{k}_{f}}$$

(4)

The assumptions used in developing this model are:

• 1. Fluid flow in the inner region (Zone 1) is governed by the infinite conductivity hydraulic fracture model in Eq. 1.

• 2. The reservoir is infinite.

• 3. Both regions could exhibit non-Newtonian flow.

• 4. Laminar and Darcy’s flow is valid.

• 5. Isothermal, single-phase and slightly compressible fluid with constant properties.

• 6. Homogenous and isotropic system.

• 7. Pseudoplastic (shear-thinning) fluid obeys Ostwald de Waele power-law relationship.

• 8. Steady state effective viscosity.

• 9. The mathematical model also assumed there is no transition region.

• 10. Warren and Root (1963) matrix pseudo-steady state transfer function is used in the mathematical model.

The solution to Eq. 1, applying to the inner region (Zone 1), after using a g-transformation as shown in “Appendix A” is

$${\overline{P} }_{D1}\left({x}_{D}, {y}_{D}, \le {x}_{Di}, {y}_{Di}\right)={C}_{1}{g}^{v1}{I}_{v1}\left(g\sqrt{sfs}\right)+{C}_{2}{g}^{v1}{K}_{v1}\left(g\sqrt{sfs}\right)$$

(5)

$${g}^{2}=\frac{4}{{\left(3-n\right)}^{2}}\left[\frac{{x}_{D}^{3-n}}{{k}_{rx}}+\frac{{y}_{D}^{3-n}}{{k}_{ry}}\right] (\mathrm{Polyanin and Zaitsev}, 2004)$$

(6)

x_Di and y_Di is the coordinate at the flood front. When n = 1 in Eq. 6, a Newtonian radial coordinate is obtained.

We have assumed homogeneous isotropic formation; hence, the relative permeability in both directions is taken to be unity.

The solution for an infinite system (Carslaw and Jaeger, 1959) is:

$${\overline{P} }_{D1}\left({x}_{w}, {y}_{w}\le {x}_{D}, {y}_{D}, \le \infty \right)=C{g}^{v}{K}_{v}\left(g\sqrt{sfs}\right)$$

(7)

The governing equation for Zone 2 in an infinite system is

$${\overline{P} }_{D2}\left({x}_{Di}, {y}_{Di}\le {x}_{D}, {y}_{D}\le \infty \right)={C}_{3}{g}^{v2}{K}_{V2}\left(g\sqrt{\alpha sfs}\right)$$

(8)

Wellbore storage C_D and skin S can be incorporated in the wellbore solutions in the Laplace space as shown in Eq. 9.

$${P}_{wD}\left(1, s, {C}_{D}, S\right)=\frac{s{P}_{wD}\left(1, s\right)+S}{\left\{s+{s}^{2}{C}_{D}\left(s{P}_{wD}\left(1, s\right)+S\right)\right\}}$$

(9)

Type curve and validation

We used the radial line source solutions developed by Ikoku and Ramey (1979), and Odeh and Yang (1979) to develop the solution for an infinite conductivity hydraulic fracture and compared the results with our 2-D analytical solution. We also used Eq. 34 in the work of Rghavan and Chen (2017) which is the analytical solution developed in their work for an infinite conductivity hydraulic fracture to obtain similar curve for flow behavior index n of 0.2, 0.6 and 1.0. The results obtained are shown in Fig. 2. As shown in Fig. 2a, b, Raghavan and Chen (2017) solution did not match other solutions at flow behavior index n of 0.2 and 0.6 except for 1.0. The reason for this discrepancy could be due to the line source solution used by Raghavan and Chen (2017) or in the conversion of their line source solution to that of an infinite conductivity hydraulic fracture.

Fig. 2

source solutions for flow behavior index n = 0.2, 0.6 and 1.0 (A&M: Alpheus and Mojeed)

Comparison of infinite conductivity hydraulic fracture solutions developed from various line

We also compared our results with that of Ertekin et al (1987) for a finite dimensionless conductivity value of π. The result is shown in Fig. 3. Ertekin et al (1987) used numerical method which probably may have contributed to the observed variation. However, the pattern remained the same.

Fig. 3

Match with Ertekin et al. Dimensionless conductivity π and constant pressure boundary

The dimensionless pressure drop for various values of n computed with the infinite reservoir described in Eq. 7 for both homogeneous and naturally fractured reservoir shown in Fig. 4a, b, respectively.

Fig. 4

Dimensionless pressure drop for an infinite conductivity hydraulic fracture in homogeneous (4a) and naturally fractured (4b) reservoirs

The plot of the dimensionless pressure drop of non-Newtonian fluid with different flow behavior index (Fig. 4) reveals that the early pressure behavior is practically the same and exhibits linear flow except in the late radial flow regime. Having validated our solution for a non-composite reservoir, we proceed to develop the solution for a composite reservoir.

Composite reservoir

The two equations used in the modeling of the composite system with an infinite conductivity hydraulic fracture in the inner zone are Eqs. 5 and 8. The details of the derivation are in “Appendix A” under composite system. The final wellbore dimensionless pressure drop equation in Laplace space is Eq. 56 in “Appendix A”. Figures 6 and  7 are generated with R_D = 2.5, alpha = 0.001 and theta = 0.1. Figure 5 demonstrates the effect of mobility and diffusivity ratios as in the work of Ambastha (1988) and Abbaszadeh and Kamal (1989). The value of n and m in Fig. 5 is 1.0 and the value of the pressure derivative must be 0.5 at the longtime radial flow when theta value is unity (1.0). As defined in “Appendix”, alpha and theta represent, respectively, the diffusivity and mobility ratios of Zone 1 to Zone 2 as shown in Eqs. 50 and 51. Since Eq. 56 is a general solution, it must replicate the case of Newtonian fluid in both zones and this is shown in Fig. 5.

Fig. 5

X_D = 1.0, ω = 0.01, λ = 10^–1, R_D = 2.5 (n = 1 for Zone 1) and (m = 1 for Zone 2); infinite reservoir

Figures 6 and 7 show the behavior of the composite reservoir when different flow behavior indices are used in the inner and outer zones. Figure 6 is for homogeneous reservoir and naturally fractured reservoir. The pressure derivatives at the late radial flow in Zone 2 is less than 0.5 because of the value of theta (mobility ratio) used which is less than 1.0. As shown in Fig. 5, when the mobility ratio is less than 1.0, the dimensionless pressure derivative of the late radial flow regime will be less than 0.5. When the mobility ratio is greater than 1.0, the dimensionless pressure derivative of the late radial flow regime will be greater than 0.5. As shown in the work of Abbaszadeh and Kamal (1989), the mobility ratio has a stronger influence on the pressure derivative behavior.

Fig. 6

XD = 0.732 (n for Zone 1) and (6a: m = 1.0 for Zone 2, 6b: m = 0.8 for Zone 2); infinite homogeneous reservoir

Fig. 7

XD = 0.732, ω = 0.01, λ = 10^–1, (n for Zone 1) and (7a: m = 1.0 for Zone 2, 7b: m = 0.8 for Zone 2); infinite naturally fractured reservoir

Limitation of model

• 1. There are many non-Newtonian viscosity models (Savins (1969)). Our mathematical model is only developed for OstWaal-de-Waele power law model. However, it is applicable to Newtonian model by setting the flow behavior index to unity.

• 2. The model assumed no transition region.

• 3. Warren and Root (1963) matrix pseudo-steady state flow into the fracture is assumed. This may not be applicable to matrix region of high natural fracture intensity where complex models like trilinear and triple-porosity models exist.

Application to practical example

Van den Hoek et al. (2012) presented three practical examples that we used to practically validate our solution. Table 1 shows the parameters used in Eqs. 56 and 9 to generate the type curves in obtaining the match for the three examples. The injected polymer is in Zone 1 with flow behavior index n, while Zone 2 contains the in situ fluid with flow behavior index m equal to 1.0. This is a case of non-Newtonian and Newtonian fluids in Zone 1 and Zone 2, respectively.

Table 1 Match parameters for the three examples

If R_D is the radial distance of the flood front, assuming a square model, then,

$$\left({x}_{Di, }{y}_{Di}\right)={R}_{D}\surd \pi$$

(10)

Example #1

Fig. 9 shows the type curve match for the falloff data in a polymer injection well after few months of injection. During radial flow, the dimensionless wellbore pressure drop and its pressure derivative for a non-composite reservoir are given by Eqs. 11 and 12, respectively.

$${P}_{WDf}=\left(\frac{1}{2}\times \frac{1}{v}\right){t}_{D}^{v}$$

(11)

$${t}_{D}\times {P}_{wDf}^{^{\prime}}=\frac{1}{2}{t}_{D}^{v}$$

(12)

On a log–log scale, a straight line can be fixed on the pressure and pressure derivative data. The slope of such straight line on the pressure derivative data is v from which the value of n can be determined

$$v=\frac{1-n}{3-n}$$

(13)

Using the dimensionless definition in Eqs. 21 and 22 in “Appendix”, Eq. 12 becomes:

$$t\times {\Delta P}^{^{\prime}}=\frac{1}{2}{\left(\frac{q}{2\pi h}\right)}^{\frac{1+n}{3-n}}{\left(\frac{{\mu }_{eff}}{{k}_{h}}\right)}^{\frac{n}{3-n}}{\left(\frac{1}{n{\left(\varnothing {c}_{t}\right)}_{t}}\right)}^{\frac{1-n}{3-n}}{t}^{\frac{1-n}{3-n}}$$

(14)

Equations 11–14 are derived from Eq. 43. The factorization and inversion of Eq. 56 for a longtime case is presented in “Appendix”. As shown in Eq. 64 in the “Appendix”, Eq. 12 cannot be applied without a correction factor. By applying the method of van den Hoek et al. (2012) to Eqs. 12 and 14, we can obtain similar expression for a composite reservoir. Thus:

$${t}_{D}\times {P}_{wDf}^{^{\prime}}=A\times \frac{1}{2}{t}_{D}^{v}$$

(15)

$$t\times {\Delta P}^{^{\prime}}=A\times \frac{1}{2}{\left(\frac{q}{2\pi h}\right)}^{\frac{1+n}{3-n}}{\left(\frac{{\mu }_{eff}}{{k}_{h}}\right)}^{\frac{n}{3-n}}{\left(\frac{1}{n{\left(\varnothing {c}_{t}\right)}_{t}}\right)}^{\frac{1-n}{3-n}}{t}^{\frac{1-n}{3-n}}$$

(16)

Equations 64–66 show that A is a function of the position of the flood front, mobility and diffusivity ratios and flow behavior index n and m. We fixed Eq. 15 on the dimensionless pressure derivative curve by computing the dimensionless pressure derivative from the values of t_D, using Eq. 12. The numerical value of A is determined by trial and error until the log–log straight line is perfectly on the non-Newtonian radial flow region of the dimensionless pressure derivatives. For example, Fig. 8 is the type curve for example #1. The straight line with the red color was drawn with Eq. 12, while the straight line with the green color was drawn with Eq. 15 with the A value of 0.8. Figure 9 shows the complete type curve match, though without the red line. The reason for Fig. 8 is to pictorially show the workflow. The value of A for the examples #2 and #3 is 0.95. This is because we used the same value of flow behavior index for the examples #2 and #3.

Fig. 8

The type curve used for example #1

Fig. 9

van den Hoek et al. (2012) example #1

van den Hoek et al. (2012) used n value of 0.6 which was derived from the straight line (dotted straight lines on Figs. 9, 10, 11) drawn by using pressure derivative equation equivalent to Eq. 16. The point at which the pressure derivative curve falls off from the straight line is considered to be the flood front. van den Hoek et al. (2012) developed an equation for estimating the transition zone. The transition zone in this case is before the estimated flood front. One parameter in the van den Hoek et al.’s (2012) formula for estimating the transition zone is the cumulative pumping time. A low estimate of the pumping time can put the transition zone before the actual flood front.

Refer to Table 1 for the parameters used to generate the type curve. In this example, both the type curve match and van den Hoek et al. (2012) methods have the same value of flow behavior index n in Zone 1. Hence the green straight line from the dimensionless pressure derivative coincided with that of van den Hoek et al. (2012) when a perfect match is obtained.

Example #2

Fig. 10 shows the type curve match for this example. The pressure data are from different injection well, and the polymer injection has been on for about nine months before the falloff test. The same procedure discussed in the example #1 was used to determine the flood front. van den Hoek et al. (2012) computed flow behavior index n of 0.6 from the straight line as described in example #1. We are able to obtain good match using the type curve method with a flow behavior index n of 0.8. We attributed the difference in the flow behavior index n to the fact that there is possibility of polymer degradation after it must have been injected into the reservoir for a considerable period of time. Moreover, the type curve match is to capture the entire behavior of the pressure data as much as possible. In this case, the computed transition zone by van den Hoek et al. (2012) is after the flood front. Our green straight line does not match that of van den Hoek et al. (2012) because of the difference in the flow behavior index.

Fig. 10

van den Hoek et al. (2012) example #2

Example #3

This injector is the same as in example #1. The type curve match is shown in Fig. 11. As indicated by van den Hoek et al. (2012), using the workflow for examples #1 and #2 is not possible because the large wellbore storage has eliminated the non-Newtonian radial flow in Zone 1 (polymer zone). van den Hoek et al. (2012) assumed a flow behavior index of 0.6 to draw the straight line. This might lead to uncertainty in the estimation of the flood front. Using a type curve match method should give a better result with lower degree of uncertainty. The flow behavior index we used is 0.8. The reason for not being able to match the early part of the pressure data could be due to the drop in the liquid level during the falloff test, a phenomenon usually experienced in the phase segregation case.

Fig. 11

van den Hoek et al. (2012) example #3

The point of the intersection of the straight line with the pressure derivative curve at best can only be the transition zone. The flood front radial dimensionless distance used in the type curves is provided in Table 1.

Discussion of the results

The examples #1 and #3 are from the same well. Therefore, we do not change the values of alpha and theta. We, however, maintained the same values for example #2.

Having developed the analytical 2-D mathematical model, our goal is to use the model in evaluating polymer flood front. van den Hoek et al.’s (2012) examples provide appropriate case for practical validation. Formation parameters can be evaluated from both zones if injection and necessary formation data are available. Using Tiab Direct Synthesis (TDS) for evaluation has been discussed extensively by Katime-Meindl and Tiab (2001), Igbokoyiand Tiab (2007) and, Omosebi and Igbokoyi(2015). However, as indicated in Eq. 64 in “Appendix”, a correction factor is needed for correcting the pressure derivative equation of non-composite system to that of a composite system. A major highlight from this study is the fact that the pressure derivative data in a composite system during non-Newtonian radial flow are strictly numerically not equal to its equivalent in the non-composite system. As earlier indicated by van den Hoek et al. (2012), a correction factor is needed to adjust the pressure derivative log–log straight line equation for non-composite system to that of a composite system before Eq. 12 can be used in the analysis or application of the TDS formulae from non-composite system.

From the three examples, we observed that as n tends to 1.0, the value of A in Eqs. 15 and 16 tends to 1.0. We have used the available field data to prove the validity of our mathematical model for the case of reservoir flooding that result in two flow behavior indices in the reservoir. Even though the flow behavior index we used in example #2 and #3 is different from that of van den Hoek et al.’s (2012), the point of intersection of the two straight lines with the pressure derivative curve on the match is practically the same in each of the examples #2 and #3. As earlier mentioned, both indicated the same transition zone in each case.

Conclusions

A 2-D general solution for evaluating fractured injection well performance with non-Newtonian fluid in a composite reservoir is developed. The computed dimensionless pressure drop is favorably compared with the wellbore infinite conductivity dimensionless fractured pressure developed from the line source solutions of Ikoku and Ramey (1979), and Odeh and Yang (1979). We also used the work of Ertekin et al (1987) to validate our solution for a finite conductivity case.

The composite mathematical model in an infinite system was applied to solve the examples presented by van den Hoek et al. (2012). Although the match obtained in examples #2 and #3 is with higher values of flow behavior index n, we have confidence in the overall results because of the consistency in the flood front that agreed with the duration of injection.

The 2-D solution is applicable to naturally fractured reservoirs and also the case of non-Newtonian/non-Newtonian composite system as in polymer flooding of a heavy crude reservoir where the heavy crude exhibits non-Newtonian behavior. As indicated by van den Hoek et al. (2012) and the longtime inversion of the analytical solution for the composite system in this study, a correction factor is needed to apply the TDS formulae developed for non-Newtonian radial flow from the non-composite system.

Appendices

Appendix A

I: Infinite conductivity hydraulic fracture

The general 2-D non-Newtonian fluid flow equation for the proposed model is

$${\frac{1}{n}\left(\frac{{k}_{fx}}{{\mu }_{e}}\right)\left(\frac{q}{2\pi xh}\right)}^{1-n}\frac{{\partial }^{2}{P}_{f}}{\partial {x}^{2}} + {\frac{1}{n}\left(\frac{{k}_{fy}}{{\mu }_{e}}\right)\left(\frac{q}{2\pi yh}\right)}^{1-n}\frac{{\partial }^{2}{P}_{f}}{\partial {y}^{2}}={\left(\phi {c}_{t}\right)}_{f}\frac{\partial {P}_{f}}{\partial t}+{\left(\phi {c}_{t}\right)}_{m}\frac{\partial {P}_{m}}{\partial t}$$

(17)

$$ \begin{aligned}&{\left(\frac{{k}_{fx}}{{\mu }_{e}}\right)\left(\frac{1}{x}\right)}^{1-n}\frac{{\partial }^{2}{P}_{f}}{\partial {x}^{2}} + {\left(\frac{{k}_{fy}}{{\mu }_{e}}\right)\left(\frac{1}{y}\right)}^{1-n}\frac{{\partial }^{2}{P}_{f}}{\partial {y}^{2}}\\ &\quad={\mathrm{n}\left(\frac{q}{2\pi h}\right)}^{n-1}\left\{{\left(\phi {c}_{t}\right)}_{f}\frac{\partial {P}_{f}}{\partial t}+{\left(\phi {c}_{t}\right)}_{m}\frac{\partial {P}_{m}}{\partial t}\right\}\end{aligned} $$

(18)

$${x}_{D}, {y}_{D}, {r}_{D} = \frac{x}{{x}_{f}}, \frac{y}{{x}_{f}}, \frac{r}{{x}_{f}}$$

(19)

$${k}_{rx}, {k}_{ry}= \frac{{k}_{fx}}{{k}_{h}}, \frac{{k}_{fy}}{{k}_{h}}$$

(20)

$${P}_{D} = \frac{{P}_{i}-{P}_{f}}{{\left(\frac{q}{2\pi h}\right)}^{n}\left(\frac{{\mu }_{e}{{x}_{f}}^{1-n}}{{k}_{h}}\right)}$$

(21)

$${t}_{D} = \frac{t}{\frac{n{\mu }_{e}{\left(\phi {c}_{t}\right)}_{t}}{{k}_{h}}{\left(\frac{2\pi h}{q}\right)}^{1-n}{x}_{f}^{3-n}}$$

(22)

$$\omega = \frac{{\left(\phi {c}_{t}\right)}_{f}}{{\left(\phi {c}_{t}\right)}_{f}+{\left(\phi {c}_{t}\right)}_{m}}$$

(23)

$$\uplambda =\delta \frac{{k}_{m}{x}_{f}^{2}}{{k}_{f}}$$

(24)

The dimensionless form of Eq. 18 is given as:

$${k}_{rx}{x}_{D}^{n-1}\frac{{\partial }^{2}{P}_{Df}}{\partial {x}_{D}^{2}} + {k}_{ry}{y}_{D}^{n-1}\frac{{\partial }^{2}{P}_{Df}}{\partial {y}_{D}^{2}}=\omega \frac{\partial {P}_{Df}}{\partial {t}_{D}}+ \left(1-\omega \right)\frac{\partial {P}_{Dm}}{\partial {t}_{D}}$$

(25)

From Warren and Root (1963),

$${\mathrm{n}\left(\frac{q}{2\pi h}\right)}^{n-1}{\left(\phi {c}_{t}\right)}_{m}\frac{\partial {P}_{m}}{\partial t}=\delta \frac{{k}_{m}}{{\mu }_{e}}\left({P}_{f}-{P}_{m}\right)$$

(25a)

In dimensionless form,

$$\left(1-\omega \right)\frac{\partial {P}_{Dm}}{\partial {t}_{D}}=\delta \frac{{k}_{m}{x}_{f}^{3-n}}{{k}_{h}}\left({P}_{Df}-{P}_{Dm}\right)$$

(25b)

$$\delta =\frac{4m\left(m+2\right)}{{l}_{m}^{2}}$$

(25c)

$$\uplambda =\frac{4j\left(j+2\right)}{{l}_{m}^{2}}\frac{{k}_{m}{x}_{f}^{3-n}}{{k}_{h}}$$

(25d)

In Eq. 25d, we have taken k_f = k_h.

Initial condition

$${P}_{Df}\left({x}_{D},{y}_{D}; {t}_{D}=0\right)=0$$

(26)

Outer boundary condition

$${P}_{Df}\left({x}_{D},{y}_{D}\le \infty {t}_{D}\ge 0\right)=0$$

(27)

The Laplace transformation of Eq. 25 is

$${k}_{rx}{x}_{D}^{n-1}\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {x}_{D}^{2}} + {k}_{ry}{y}_{D}^{n-1}\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {y}_{D}^{2}}=sf\left(s\right){\overline{P} }_{Df}$$

(28)

where

$$sf\left(s\right)=s\frac{\omega \left(1-\omega \right)s+\uplambda }{\left(1-\omega \right)s+\uplambda }$$

(29)

We defined g-transformation as

$${g}^{2}=\frac{4}{{\left(3-n\right)}^{2}}\left[\frac{{x}_{D}^{3-n}}{{k}_{rx}}+\frac{{y}_{D}^{3-n}}{{k}_{ry}}\right]$$

(30)

$$\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {x}_{D}^{2}}=\frac{{\partial }^{2}g}{\partial {x}_{D}^{2}}\frac{\partial {\overline{P} }_{Df}}{\partial g}+{\left(\frac{\partial g}{\partial {x}_{D}}\right)}^{2}\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {g}^{2}}$$

(31)

Using the same derivative transformation for y_D, apply to Eq. 28 with relative permeability of unity gave:

$$\frac{{\partial }^{2}{\overline{P} }_{Df}}{\partial {g}^{2}} + \left(1+\frac{2\left(1-n\right)}{\left(3-n\right)}\right)\frac{1}{g}\frac{\partial {\overline{P} }_{Df}}{\partial g}=sf\left(s\right){\overline{P} }_{Df}$$

(32)

Define v as:

$$v=\frac{\left(1-n\right)}{\left(3-n\right)}$$

(33)

Solution to Eq. 33 in an infinite system is:

$${\overline{P} }_{Df}\left({x}_{w}, {y}_{w}\le {x}_{D}, {y}_{D}, \le \infty ,s\right)=C{g}^{v}{K}_{v}\left(g\sqrt{sfs}\right)$$

(34)

For infinite conductivity hydraulic fracture:

$${\overline{P} }_{WDf}=\frac{1}{2s}{\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\underset{-1}{\overset{1}{\int }}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}{K}_{\frac{1-n}{3-n}}\left(\frac{2}{3-n}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}\right)\surd \left(sfs\right)\partial {x}_{D}$$

(35)

By making

$$u=\frac{2}{3-n}{\left(0.732-{x}_{D}\right)}^{\frac{3-n}{2}}\surd sfs$$

(36)

$${\overline{P} }_{WDf}=\frac{1}{2s\surd sfs}{\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\left\{\underset{0}{\overset{\frac{2}{3-n}{1.732}^{\frac{3-n}{2}}\surd sfs}{\int }}{K}_{v}\left(u\right)\partial u+\underset{0}{\overset{\frac{2}{3-n}{0.268}^{\frac{3-n}{2}}\surd sfs}{\int }}{K}_{v}\left(u\right)\partial u\right\}$$

(37)

At the early linear flow, sfs is large and is approximately sω. By using the expression in Raghavan and Chen (2017) in Eq. 40 of their paper, we can show that

$${\overline{P} }_{WDf}=\frac{1}{2s\surd sfs}{\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\pi sec\left(\frac{\pi \frac{1-n}{3-n}}{2}\right)$$

(38)

At early time, the expression in Eq. 38 for all values of n $0\le n\le 1$ gave:

$${P}_{WDf}=\surd \left(\pi \frac{{t}_{D}}{\omega }\right)$$

(39)

For homogeneous formation when ω = 1;

$${P}_{WDf}=\surd \left(\pi {t}_{D}\right)$$

(39a)

For a small value of u

$${K}_{v}\left(u\right)\approx \frac{1}{2}{\left(\frac{1}{2}u\right)}^{-v}\Gamma \left(v\right)$$

(40)

Therefore, for a small of u Eq. 37 becomes:

$${\overline{P} }_{WDf}=\frac{1}{2s\surd sfs}{\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\left\{\underset{0}{\overset{\frac{2}{3-n}{1.732}^{\frac{3-n}{2}}\surd sfs}{\int }}\frac{1}{2}{\left(\frac{1}{2}u\right)}^{-v}\Gamma \left(v\right)\partial u+\underset{0}{\overset{\frac{2}{3-n}\frac{2}{3-n}{0.268}^{\frac{3-n}{2}}\surd sfs}{\int }}\frac{1}{2}{\left(\frac{1}{2}u\right)}^{-v}\Gamma \left(v\right)\partial u\right\}$$

(41)

And

$${\overline{P} }_{WDf}=\frac{1}{4s\surd sfs}{\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}{\left(\frac{1}{2}\right)}^{-v}\Gamma \left(v\right)\left\{{\left.\left(\frac{{u}^{-v+1}}{-v+1}\right)\right|}_{0}^{\frac{2}{3-n}{1.732}^{\frac{3-n}{2}}\surd sfs}+{\left.\left(\frac{{u}^{-v+1}}{-v+1}\right)\right|}_{0}^{\frac{2}{3-n}{0.268}^{\frac{3-n}{2}}\surd sfs}\right\}$$

(42)

The factorization of Eq. 42 gave:

$${P}_{WDf}=\left(\frac{1}{2}\times \frac{1}{v}\right){t}_{D}^{v}$$

(43)

Equation 43 is the radial flow regime approximation.

II: Infinite Conductivity Hydraulic Fracture in a Composite Reservoir

The two equations for the composite system in an infinite system are:

$${\overline{P} }_{D1}\left({x}_{D}, {y}_{D}, \le {x}_{Di}, {y}_{Di}\right)={C}_{1}{g}^{v1}{I}_{v1}\left(g\sqrt{sfs}\right)+{C}_{2}{g}^{v1}{K}_{v1}\left(g\sqrt{sfs}\right)$$

(44)

for the inner region with infinite conductivity hydraulic fracture and,

$${\overline{P} }_{D2}\left({x}_{Di}, {y}_{Di}\le {x}_{D}, {y}_{D}\le \infty \right)={C}_{3}{g}^{v2}{K}_{V2}\left(g\sqrt{\alpha sfs}\right)$$

(45)

for the outer region.

$$v1=\frac{\left(1-n\right)}{\left(3-n\right)}$$

(46)

and

$$v2=\frac{\left(1-m\right)}{\left(3-m\right)}$$

(47)

where n and m are the flow behavior indices in the inner and outer region, respectively. By considering g spatial variable as an equivalent radial distance (Vongvuthipornchai and Raghavan 1987; Equation B-9).

$$\frac{\partial {\overline{P} }_{D2}}{\partial g}=-\theta \frac{1}{s{g}_{i}^{m}}$$

(48)

$$\frac{\partial {\overline{P} }_{D1}}{\partial g}=-\frac{1}{s{g}_{i}^{n}}$$

(49)

$$\alpha =\frac{m{\left(\frac{\varphi {c}_{t}{\mu }_{eff}}{k}\right)}_{2}{\left(\frac{2\pi {g}_{w}h}{q}\right)}^{n-m}}{n{\left(\frac{\varphi {c}_{t}{\mu }_{eff}}{k}\right)}_{1}}$$

(50)

$$\theta ={\frac{{k}_{1}}{{\mu }_{1}}\frac{{\mu }_{2}}{{k}_{2}}\left(\frac{q}{2\pi {g}_{w}h}\right)}^{m-n}$$

(51)

At the interface P_D1 = P_D2.Therefore,

$${C}_{3}=\frac{{g}_{i}^{v1}\left\{{C}_{1}{I}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right){+C}_{2}{K}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)\right\}}{{{g}_{i}^{v2}K}_{v2}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right)}$$

(52)

$$\frac{\partial {\overline{P} }_{D2}}{\partial g}=-{C}_{3}{g}^{v2}\surd \left(\alpha sfs\right){K}_{v2-1}\left(g\surd \left(\alpha sfs\right)\right)$$

(53)

Combining Eqs. 48 and 53, at the interface;

$${C}_{3}=\frac{{\theta g}_{i}^{-m-v2}}{{s\sqrt{\left(\alpha sfs\right)}K}_{v2-1}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right)}$$

(54)

Combining Eqs. 52 and 54.

$${C}_{1}=\frac{{\theta g}_{i}^{-m-v1}{K}_{v2}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right)}{{s\sqrt{\left(\alpha sfs\right)}K}_{v2-1}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right){I}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}-\frac{{C}_{2}{K}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}{{I}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}$$

(55)

Substituting Eq. 55 in Eq. 44, the infinite conductivity hydraulic fracture dimensionless pressure drop in a composite system becomes:

$${\overline{P} }_{WDf}={\frac{1}{2s}\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\left\{\frac{{\theta g}_{i}^{-m-v1}{K}_{v2}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right)}{{\sqrt{\left(\alpha sfs\right)}K}_{v2-1}\left({g}_{i}\sqrt{\left(\alpha sfs\right)}\right){I}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}-\frac{{K}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}{{I}_{v1}\left({g}_{i}\sqrt{\left(sfs\right)}\right)}\right\}\underset{-1}{\overset{1}{\int }}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}{I}_{\frac{1-n}{3-n}}\left(\frac{2}{3-n}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}\right)\sqrt{\left(sfs\right)}\partial {x}_{D}+{\frac{1}{2s}\left(\frac{2}{3-n}\right)}^{\frac{1-n}{3-n}}\underset{-1}{\overset{1}{\int }}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}{K}_{\frac{1-n}{3-n}}\left(\frac{2}{3-n}{\left\{\surd {\left(0.732-{x}_{D}\right)}^{2}\right\}}^{\frac{3-n}{2}}\right)\sqrt{\left(sfs\right)}\partial {x}_{D}$$

(56)

Observation of Eq. 56 revealed that the Bessel terms in the bracket of the coefficient of the first integral tend to zero at the large value of sfs which corresponds to the early flow regime. Hence, we are left with the second integral which will give the early linearly flow regime as that of Eq. 39.

Longtime evaluation of Eq. 56

For a small value of u

$${I}_{v}\left(u\right)\approx {\left(\frac{1}{2}u\right)}^{v}/\Gamma \left(v+1\right)$$

(57)

At longtime when the Laplace variable s is small, sfs approximates to s.

By applying Eqs. 36, 40 on 56, the longtime approximation of Eq. 56 in real dimensionless quantity is:

$${P}_{WDf}={B}_{1}+{B}_{2}+{B}_{3}$$

(58)

where.

$${\overline{B} }_{1}=\frac{\theta {g}_{i}^{-m-2{v}_{1}-2{v}_{2}+1}{\alpha }^{-{v}_{2}}\left({v}_{2}-1\right){{\left(\frac{1}{2}\right)}^{-2{v}_{2}+2}\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{\left({v}_{1}+1\right)\Gamma \left({v}_{1}+1\right){s}^{{1+v}_{2}}}$$

(59)

$${B}_{1}=\frac{\theta {g}_{i}^{-m-2{v}_{1}-2{v}_{2}+1}{\alpha }^{-{v}_{2}}\left({v}_{2}-1\right){{\left(\frac{1}{2}\right)}^{-2{v}_{2}+2}\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{\left({v}_{1}+1\right)\Gamma \left({v}_{1}+1\right)\Gamma \left({v}_{2}+1\right)}{t}_{D}^{{v}_{2}}$$

(60)

$${\overline{B} }_{2}=-\frac{\Gamma \left({v}_{1}\right){\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{{{2}^{2-{v}_{1}}g}_{i}^{2{v}_{1}}\left({v}_{1}+1\right){\mathrm{s}}^{\frac{{v}_{1}}{2}+1}}$$

(61)

$${B}_{2}=-\frac{\Gamma \left({v}_{1}\right){\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{{{2}^{2-{v}_{1}}g}_{i}^{2{v}_{1}}\frac{{v}_{1}}{2}\left({v}_{1}+1\right)\Gamma \left(\frac{{v}_{1}}{2}\right)}{t}_{D}^{\frac{{v}_{1}}{2}}$$

(62)

$${B}_{3}=\frac{1}{2{v}_{1}}{t}_{D}^{{v}_{1}}$$

(63)

Therefore,

$${t}_{D}\times {P}_{wDf}^{^{\prime}}={A}_{1}{t}_{D}^{{v}_{2}}-{A}_{2}{t}_{D}^{\frac{{v}_{1}}{2}}+\frac{1}{2}{t}_{D}^{{v}_{1}}$$

(64)

$${A}_{1}=\frac{\theta {g}_{i}^{-m-2{v}_{1}-2{v}_{2}+1}{\alpha }^{-{v}_{2}}\left({v}_{2}-1\right){v}_{2}{{\left(\frac{1}{2}\right)}^{-2{v}_{2}+2}\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{\left({v}_{1}+1\right)\Gamma \left({v}_{1}+1\right)\Gamma \left({v}_{2}+1\right)}$$

(65)

$${A}_{2}=\frac{\Gamma \left({v}_{1}\right){\left(\frac{2}{3-n}\right)}^{2{v}_{1}+1}\left({1.732}^{2-n}+{0.268}^{2-n}\right)}{{{2}^{2-{v}_{1}}g}_{i}^{2{v}_{1}}\left({v}_{1}+1\right)\Gamma \left(\frac{{v}_{1}}{2}\right)}$$

(66)

Following van den Hoek et al.’s (2012) method and when m = 1.0, we can represent Eq. 64 as;

$${t}_{D}\times {P}_{wDf}^{^{\prime}}=A\times \frac{1}{2}{t}_{D}^{{v}_{1}}$$

(67)

Note that when m = 1.0, v₂ is zero and A₁ vanishes. A is a factor to be determined by trial and error as described in the three examples.