1. Introduction

Due to the rock structure, mechanical properties and heterogeneity of ground stress, the annulus formed by drilling tends to be irregular (Chen et al. 2008; Xu 2016; Qi et al. 2018; Han et al. 2018; Chen et al. 2020). As early as 1995, Aadnoy pointed out that most annulus in the North Sea were non-circular or elliptical. It has recently been found that the annulus is more likely to expand during air drilling, forming an elliptical annulus (Xu, et al. 2016; Di et al. 2015). Figure 1 shows the multi-arm caliper test results and the annulus strain simulation results under non-uniform ground stress of a well in the Shunbei Oilfield. It can be seen from the figure: The actual annulus is a typical irregular circular annulus, with the proportion of the maximum annulus diameter to the minimum annulus diameter mostly within 1.2; the annulus shape obtained by finite element simulation under non-uniform ground stress is also an irregular circle; the annulus is the closest to an elliptical shape.

Figure.1
figure 1

Double caliper logging results a and simulation results of uniform ground stress b and non-uniform ground stress c annulus strain of a well in Shunbei Oilfield

Full size image

Non-Newtonian fluids generally refer to fluids other than Newtonian fluids, that is, the shear stress of the fluids has a nonlinear relationship with the shear rate (Tang 2016; Chlebicka et al. 2021). The constitutive equation models commonly used to characterize their rheological parameters are Bingham Plastic Model, Power-Law Model, H-B Model (or Yield Power Law Model) and Casson Model. Most of the fluids in the drilling engineering are non-Newtonian fluids, and the rheological parameters of drilling fluids have excellent accordance with the H–B model (Huang and Yang 1981).

Scholars have carried out a large number of theoretical and experimental studies on the pressure drop in regular circular annulus. Filip and David (2003) analyzed the axial laminar flow of H-B fluids in the concentric annulus using the semi-analytical models. Gjerstad (2012) established an H-B fluids circular pipe laminar flow approximate model for the real-time optimization of drilling opens. Fan (2018) proposed a generalized hydraulic calculation method to study the fluids flow laws of H-B fluids in the eccentric annulus. He (2016) established a simplified model of pressure drop prediction for H-B fluids in concentric eccentric annulus to calculate the pressure drop in concentric or eccentric annulus of circular annulus. Ferroudji (2020) used the finite volume method (FVM) to study the laminar flow characteristics of power law fluids in eccentric annulus. Ahmed (2008) evaluated the laminar flow law of Newtonian fluids, power law fluids and H-B fluids in concentric or eccentric annulus through an indoor test device. In addition, some scholars (Peng et al. 2013; Sayindla et al. 2019; Zhang et al. 2016; Alade, et al. 2019; He 2005; Puranik et al. 2021) have used mathematical software or computational fluids dynamics software to study the flow of H-B fluids under different conditions in regular circular annulus, but none of them considered the elliptical shape of the annulus.

Domestic research on the pressure drop of H-B fluids flow in elliptical annulus is still in its infancy. At this stage, most of the numerical simulations are carried out with the help of mathematical software and computational fluids dynamics software. Xu (2020), Tang (2019), Alegria (2012) established a numerical model for yielding power law fluids in the eccentric elliptical annulus based on the assumption of narrow-slot flow model and systematically evaluated the influence of different parameters on the pressure drop. Ferroudji (Hicham et al. 2019) analyzed the parameters affecting pressure drop of power-law fluid in horizontal annulus for laminar and turbulent flows by CFD. Zhang (2019), Tang (2018), Wang (2018) established a numerical model for calculating the pressure drop of H-B laminar flow in the CAEW by correcting the hydraulic diameter and used computational fluids dynamics simulation results to verify the effectiveness of the model, which achieved accurate prediction of the pressure drop in the CAEW. Alegría (2012) and Foroushan (2020) established an analytical model to analyze the annulus pressure drop in an elliptical wellbore, but without considering the effect of the flow core in the solution process, as shown in Fig. 2.

Fig. 2
figure 2

Elliptical annulus cross section a and Velocity profile b by Alegría and Foroushan

Full size image

Although the numerical model and analytical model achieved accurate prediction of the pressure drop in the CAEW, the prediction model was still relatively complex and not suitable for large-scale application. In order to predict the pressure drop of the H-B fluids laminar flow in the CAEW accurately and conveniently, this paper established an analytical model firstly and clarified the influence of different parameters on the pressure drop was clarified through analysis. Finally, the CAEW dimensionless pressure drop regression model was established through multiple regression.

2. Analytical model

An analytical model was established to accurately predict the pressure drop of the H-B fluids in the CAEW. The basic assumptions are (1) The annulus is a regular elliptical annulus; (2) The fluids rheological parameters meet the H-B model; (3) The drill string is completely centered in the elliptical annulus; (4) The fluids in the annulus are a single-phase steady-state adiabatic laminar flow and the flow in the radial and circumferential directions is ignored; (5) The compressibility of the formation and drill string is ignored; (6) The a/b is between 1.0 and 1.2.

Figure 3b is a geometric schematic of CAEW. According to the geometric relationship in the figure, the distance between the well wall and the center of the annulus at any θ can be determined as follows:

$$h\left( \theta \right) = \sqrt {a^{2} \cos^{2} \theta + b^{2} \sin^{2} \theta }$$
(1)
Fig. 3
figure 3

Force analysis of H-B fluids in the CAEW(Overall schematic (a); geometric schematic (b) of CAEW and micro-elements in the annulus(c))

Full size image

A micro-element segment was selected from the annulus for force analysis. Figure 3c shows a schematic diagram of the force of the micro-element. Based on force balance, we can get:

$$\left( {P_{s} + \Delta P_{s} } \right)\left( {2\pi r} \right)\Delta r - P_{s} \left( {2\pi r} \right)\Delta r\; = \;\tau \left( {2\pi r} \right)\Delta L - \left( {\tau + \Delta \tau } \right)2\pi \left( {r + \Delta r} \right)\Delta L$$
(2)

Sorting out and ignoring the higher-order terms (\(\Delta \tau /r\)), we obtain:

$$\frac{{\Delta P_{s} }}{\Delta L} + \frac{\tau }{r} + \frac{\Delta \tau }{{\Delta r}} = 0$$
(3)

When \(r \to 0\),\(L \to 0\), the differential form of the flow momentum equation of the micro-element in the CAEW can be obtained as follows:

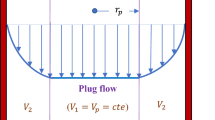
$$\frac{1}{r}\frac{1}{{{\text{d}}r}}\left( {r\tau_{{{\text{rz}}}} } \right) = \frac{\partial P}{{\partial L}}$$
(4)

The current analytical model usually does not consider the influence of the flow core on the annulus flow. It can be seen from Fig. 4 that the flow of the H–B fluids in the annulus can be divided into three areas (area I, II and III). Area I and III are shear flow regions. Both velocity profile and shear stress profile in the regions change with the radial distance. Area II is the flow core area where the velocity remains constant. The general solution of the momentum equation is the shear stress of fluids flow.

Fig. 4
figure 4

Flow velocity profile of yield power law fluids in the CAEW

Full size image

Sorting Eq. 4 while integrating both sides, we get:

$$\tau_{{\text{r}}} = - \frac{1}{2}\frac{\Delta P}{{\Delta L}}r^{2} + C$$
(5)

Combined with the shear stress at the inner and outer boundaries of the flow core τrz(r1(θ),θ) = τ0 and τrz(r2(θ),θ) = -τ0, we can get the annular shear stress profile as follows:

$$\tau = \frac{1}{2}\frac{\Delta P}{{\Delta L}}\left( {\frac{{\tau_{0} r_{1} \left( \theta \right) + \frac{1}{2}\frac{\Delta P}{{\Delta L}}r_{1} \left( \theta \right)^{2} }}{{\frac{1}{2}\frac{\Delta P}{{\Delta L}}r}} - r} \right)$$
(6)

According to the mechanical balance relationship, the shear stress received by the flow core and the compressive stress at both ends of the flow core should be balanced:

$$\Delta P_{{\text{s}}} A = \tau_{0} \left( {S_{1} + S_{2} } \right)$$
(7)

According to the geometric relationship:

$$A = \pi \left( {r_{2} \left( \theta \right)^{2} - r_{1} \left( \theta \right)^{2} } \right)$$
(8)
$$S_{1} + S_{2} = 2\pi \Delta L\left( {r_{1} \left( \theta \right) + r_{2} \left( \theta \right)} \right)$$
(9)

Substituting Eqs. 8 and 9 into Eq. 7, we get:

$$\tau_{0} = \frac{1}{2}\frac{\Delta P}{{\Delta L}}\left( {r_{2} \left( \theta \right) - r_{1} \left( \theta \right)} \right)$$
(10)

The general solution of the momentum equation can be obtained by substituting Eq. 10 into Eq. 6:

$$\tau_{{{\text{rz}}}} \left( {r,\theta } \right) = \frac{1}{2}\frac{\Delta P}{{\Delta L}}\left[ {\frac{{r_{1} \left( \theta \right)r_{2} \left( \theta \right)}}{r} - r} \right]$$
(11)

The constitutive equation of annulus fluids satisfies the H–B model, and the constitutive equations of area I and area III can be obtained as follows:

$$\tau_{{{\text{rz}}}} = \pm \tau_{0} + K\left( {{{ \pm {\text{d}}u} \mathord{\left/ {\vphantom {{ \pm {\text{d}}u} {{\text{d}}r}}} \right. \kern-\nulldelimiterspace} {{\text{d}}r}}} \right)^{{\text{n}}}$$
(12)

When in area I, all the above equations are taken as “ + ” signs, and when in area III, all are taken as “-” signs.

Bringing the constitutive equations of areas I and III into the shear stress profile equation and combining the velocity boundary conditions of region I and III u1(rp,θ) = u3(rh(θ),θ) = 0, we can obtain the velocity equations for areas I and III as follows:

$$\left\{ \begin{gathered} u_{1} (r,\theta ) = K^{{ - {1 \mathord{\left/ {\vphantom {1 {\text{n}}}} \right. \kern-\nulldelimiterspace} {\text{n}}}}} \int_{{{\text{r}}_{{\text{p}}} }}^{{\text{r}}} {\left[ {\tau_{{{\text{rz}}}} \left( {r,\theta } \right) - \tau_{0} } \right]}^{{\frac{1}{{\text{n}}}}} {\text{d}}r \hfill \\ u_{3} (r,\theta ) = K^{{ - {1 \mathord{\left/ {\vphantom {1 {\text{n}}}} \right. \kern-\nulldelimiterspace} {\text{n}}}}} \int_{{\text{r}}}^{{{\text{h}}\left( \theta \right)}} {\left[ { - \tau_{{{\text{rz}}}} \left( {r,\theta } \right) - \tau_{0} } \right]}^{{\frac{1}{{\text{n}}}}} {\text{d}}r \hfill \\ \end{gathered} \right.$$
(13)

Based on the mechanical equilibrium in the flow core, the shear stress of the core is the same as the pressure drop at both ends. The thickness of the annulus flow core is obtained as σp = 2τ0/(ΔP/ΔL). Combining with the geometric relationship in Fig. 3, we can know:

$$r_{2} \left( \theta \right) = r_{1} \left( \theta \right) + \sigma_{p}$$
(14)

The velocity in the flow core is equal, that is, the axial velocity at the junction of the areas I and III and the flow core are the same:

$$u_{1} (r_{1} ,\theta ) = u_{3} (r_{2} ,\theta ){ = }u_{2} (r,\theta )$$
(15)

Integrating the velocity in the annulus, we can obtain the annulus flow under the assumed condition of annulus pressure gradient:

$$Q = \int\limits_{0}^{2\pi } {\left[ {\int\limits_{{{\text{r}}_{{\text{p}}} }}^{{{\text{r}}_{1} \left( \theta \right)}} {u_{1} \left( {r,\theta } \right)} r{\text{d}}r + \int\limits_{{{\text{r}}_{1} \left( \theta \right)}}^{{{\text{r}}_{2} \left( \theta \right)}} {u_{2} \left( {r,\theta } \right)} r{\text{d}}r + \int\limits_{{{\text{r}}_{2} \left( \theta \right)}}^{{{\text{h}}\left( \theta \right)}} {u_{3} \left( {r,\theta } \right)} r{\text{d}}r} \right]{\text{d}}\theta }$$
(16)

In this paper, the professional mathematical software MATLAB was used to compile a calculation program for predicting the pressure drop of the H–B fluids laminar flow in CAEW. The specific calculation program flow is as follows:

(1) Assume an annulus pressure gradient (∆P/∆L) and enter other basic parameters required for calculation such as fluids rheological parameters, annulus geometric parameters and actual flow (Qactual);

(2) Calculate the thickness of the flow core and determine the boundary of the flow core at different angles θ in the annulus;

(3) Calculate the annulus flow under the assumed condition of annulus pressure gradient (Qassumption);

(4) When Qactual = Qassumption, the assumed pressure gradient is the pressure gradient obtained.

3. Parametric study

In order to define the influence of different parameters on the pressure drop of the H-B fluids laminar flow in CAEW, the influencing factors were analyzed using this model. Figure 5 shows the influence of different fluids yield values and consistency index on the pressure gradient. From the figure, we can know that the pressure gradient increases linearly with the increase in the fluids yield value and consistency index. The possible reason is that the shear stress increases linearly with the fluids yield value and consistency index, resulting in a linear increase in the pressure gradient.

Fig. 5
figure 5

The influence of yield value of fluids (a) and consistency index (b) on the pressure gradient

Full size image

Figure 6 shows the influence of fluidity index and the proportion of the inner and outer diameters on the pressure gradient. It can be seen from the figure that the pressure gradient exponentially grows with the fluidity index and the proportion of the inner and outer diameters. The fluids shear stress increases exponentially with the fluidity index, resulting in an exponential increase in the pressure gradient. When the annulus size is constant, the annulus flow area decreases exponentially with the increase in the proportion of the inner and outer diameters. The lower the flow area, the greater the fluids flow resistance, which ultimately results in the exponential increase in pressure gradient with the increase in the proportion of the inner and outer diameters.

Fig. 6
figure 6

The influence of fluidity index (a) and proportion of inner and outer diameter (b) on the pressure gradient

Full size image

Figure 7 shows the influence of the average velocity and the proportion of the major and minor axes on the pressure gradient. The pressure gradient increases quasi-linearly with the average velocity and increases exponentially with the proportion of the major and minor axes. The greater the average velocity, the greater the pressure gradient. The annulus flow area decreases exponentially with the increase in the proportion of the major and minor axes, which results in an exponential increase in the pressure gradient with the increase in the proportion of the major and minor axes.

Fig. 7
figure 7

The influence of the average velocity of annulus (a) and the proportion of the major and minor axes (b) on the pressure gradient

Full size image

The dimensionless pressure drop gradient is the proportion of the pressure gradient in the elliptical annulus to the circular annulus under the same other conditions.

$$R = \frac{{\left( {\Delta P/\Delta L} \right)_{{{\text{elliptical}}}} }}{{\left( {\Delta P/\Delta L} \right)_{{{\text{circular}}}} }}$$
(17)

Through parameter analysis, it is found that the pressure gradient changes quasi-linearly with the yield value of fluids, annulus average flow velocity, and consistency index. Combining with the definition of dimensionless pressure drop, it can be judged that the dimensionless pressure gradient hardly changes with the change of the yield value of fluids, annulus average flow velocity, and consistency index. Conversely, the fluidity index, the proportion of the inner and outer diameter and the proportion of the major and minor axes have a relatively large influence on the dimensionless pressure gradient.

4. Regression model

Compared with the numerical model and CFD simulation, the analytical model is simpler to calculate pressure drop of the H-B fluids in the CAEW, but it also requires a certain numerical calculation method, which is not convenient for field engineers to directly apply. In order to accurately and conveniently predict the pressure drop of the H-B fluids in the CAEW, this paper establishes a regression model that does not require numerical calculation. Figure 8 shows the variation in the dimensionless pressure gradient with the proportion of the major and minor axes when the average velocity, the yield value of the drilling fluids and the consistency index are different. It can be seen from the figure that when fluidity index, the proportion of inner and outer diameter and eccentricity are constant, the dimensionless pressure gradient is almost irrelevant of the changes of the average velocity, the yield value of the drilling fluids and the consistency index.

Fig. 8
figure 8

Variation in the dimensionless pressure gradient with the proportion of major and minor axes at different annulus average velocity, drilling fluids yield value and consistency index

Full size image

Figure 9 shows the variation in the dimensionless pressure gradient with the proportion of the major and minor axes under different fluids fluidity indexes and the proportion of the inner and outer diameters. It can be seen from the figure that the dimensionless pressure gradient varies significantly with the fluidity index of the drilling fluids, the proportion of the inner and outer diameter, and the proportion of the major and minor axes. Therefore, the regression relationship between the dimensionless pressure gradient and the drilling fluids fluidity index, the annulus inner and outer diameter proportion, and the major-minor axis proportion can be established to calculate the pressure drop in the CAEW. In this paper, the ordinary least squares were used for regression. The difficulty of regression lies in the design of function type. With reference to the analysis results of influencing factors by analytical model, a new regression model for predicting dimensionless pressure gradient in CAEW was developed.

Fig. 9
figure 9

Variation law of the dimensionless pressure gradient with the proportion of major and minor axes under different fluids fluidity index (a) and the proportion of inner and outer diameter (b)

Full size image

First of all, since the proportion between the major and minor axes is in a quasi-linear relationship with the dimensionless pressure gradient, the function type of this parameter is set as polynomial:

$$R = \sum\limits_{{{\text{i}} = 1}}^{{\text{n}}} {x_{{\text{i}}} \eta^{{{\text{i}} - 1}} } \left( {n = 1,2,3, \cdots } \right)$$
(18)

As shown in Table 1 and Fig. 10, it is found from preliminary polynomial regression that the regression result of the dimensionless pressure gradient to the proportion of the major and minor axes can be satisfied when i is set to 3.

Table 1 Preliminary regression results
Full size table
Fig. 10
figure 10

Preliminary regression results

Full size image

In Eq. 18, xi is determined by the drilling fluids fluidity index and the proportion of inner and outer diameter. Since these parameters have an exponential relationship with the dimensionless pressure gradient, the function type of these parameters is set as exponential:

$$x_{{\text{i}}} = A_{{\text{i}}} n^{{{\text{B}}_{{\text{i}}} }} K_{{\text{d}}}^{{{\text{C}}_{{\text{i}}} }}$$
(19)

Finally, the calculation results of the analytical model are brought into Eq. 19. The coefficients of each term can be calculated to establish a regression model between the dimensionless pressure gradient and the fluidity index, the proportion of the inner and outer diameter, the proportion of the major and minor axes. The regression model for the dimensionless pressure gradient of the H–B fluids in the CAEW is specifically expressed as follows:

$$R = \sum\limits_{{{\text{i}} = 1}}^{3} {A_{{\text{i}}} \eta^{{{\text{i}} - 1}} n^{{{\text{B}}_{{\text{i}}} }} K_{{\text{d}}}^{{{\text{C}}_{{\text{i}}} }} }$$
(20)

where Ai, Bi and Ci are regression undetermined coefficients and their specific values are shown in Table 2.

Table 2 Dimensionless pressure gradient regression undetermined coefficients Ai, Bi and Ci
Full size table

Equation 20 is the dimensionless pressure gradient regression model of the H-B fluids flow in CAEW. The adaptation conditions of the model are 0.4 ≤ Kd ≤ 0.75, 1.0 ≤ η ≤ 1.2 and 0.4 ≤ n ≤ 1.

5. Validation of the regression model

The calculation results of the analytical model and the regression model were compared to verify the accuracy of the new model. The main basic input parameters of the comparative analysis are τ0 = 0 ~ 30 Pa, K = 0.05 ~ 2.0 Pa.sn, n = 0.4 ~ 1.0, rh = 76.2 mm, η = 1.0 ~ 1.2, v = 0.1 ~ 1.3 m/s. Figure 11 is the comparative results of the dimensionless pressure gradient analytical model and the regression model. It can be seen from the figure that the predicted results of the regression model are in excellent agreement with the analytical model, with the error bars almost within ± 10%.

Fig. 11
figure 11

Comparative analysis results of the dimensionless pressure gradient analytical model and the regression model

Full size image

According to Eq. 17, the new model can calculate the pressure gradient in the elliptical annulus combined with the simplified model in the concentric circular annulus (Tang, et al. 2016). The most effective way to verify the new regression model is to directly compare and analyze the model results with the experimental measurements. However, there are few experimental reports on elliptical annulus flows. In order to further verify the validation of the new regression model, existing numerical model for H-B fluids flow in the CAEW (Alegria, et al. 2012) was introduced. Tables 3 and 4 are the main input parameters for comparative analysis. Figure 12 compares the result calculated by the existing numerical model with that by the new regression model. It can be found that the calculation results of the regression model and the existing numerical model are very consistent, with the error bars mostly within ± 10%, demonstrating that the new regression model can predict the pressure drop in the CAEW without complex numerical calculation method.

Table 3 Annular geometric parameters
Full size table
Table 4 Rheological parameters
Full size table
Fig. 12
figure 12

Comparative analysis results of the pressure gradient existing model and the regression model when the fluids type is H-B fluids (a) and the fluids type is PL fluids (b)

Full size image

6. Conclusions

An analytical model was established to analyze the influencing factors of pressure drop of H-B fluids in the CAEW. Based on the main influencing factors, a dimensionless pressure gradient regression model for the CAEW was established. The main conclusions are as follows:

  1. (1)

    The pressure gradient increases linearly with the increase in fluids yield value and consistency index and increases quasi-linearly with the average flow velocity. It also exponentially increases with the increase in fluids fluidity index, the proportion of the inner and outer diameter and the proportion of the major and minor axes of ellipse annulus.

  2. (2)

    The calculation results of the regression model are in excellent agreement with those of the analytical model and the existing model. The error bands are mostly within ± 10%, demonstrating that the regression model can accurately and rapidly predict the dimensionless pressure gradient in the CAEW.