Introduction

Seismic data contains amplitude with time and can provide only interface information of subsurface whereas well log data can provide detailed layer information but they are generally very sparse. To get detailed information about rocks and fluids of the subsurface in the inter-well region, one needs to combine seismic and well log data together. The seismic inversion technique combines seismic as well as well log data together to provide detailed information of the subsurface. Seismic inversion is a technique for extracting a high-resolution subsurface model of rock and fluid properties from low-resolution seismic reflection data by using high-frequency well-log data (Krebs et al. 2009; Maurya et al. 2020).

Seismic inversion techniques have been frequently employed in the petroleum sector to find hydrocarbon-bearing layers in the subsurface from seismic data (Bosch et al. 2010; Maurya and Singh 2016). Pre-stack simultaneous inversion, elastic impedance inversion, recursive inversion, model-based inversion, sparse spike inversion (which incorporates Linear programming and Maximum likelihood inversion), colored inversion, band-limited inversion, and other methods are available for seismic inversion. In this study, seismic reflection data from the Krishna Godavari (KG) basin in India is utilized to estimate subsurface acoustic impedance using maximum likelihood seismic inversion (MLSI) and model-based seismic inversion (MBSI) techniques. The justification for using these inversion approaches is because they are reliable and fast at computing the subsurface model (Russell and Hampson 1991; Maurya and Sarkar 2016). Other approaches, such as colored inversion, are also quick, but they only give an average fluctuation of the rock characteristics (Russell and Hampson 1991).

The MLSI approach uses the Maximum Likelihood Deconvolution (MLD) theory to convert seismic data to reflectivity series. The MLD algorithm was developed in 1982 by Dr. Jerry Mendel at the University of Southern California (Russell 1988; Maurya and Singh 2019). Later, the method was well-publicized by Kormylo and Mendel in (1983) and Chi et al. in (1985). The application of Kormylo and Mendel's created theory to real data is difficult, so Hampson and Russell in 1985 proposed a version that is simple to utilize for both synthetic as well as real data sets. The MLD, according to Hampson and Russell, can be used to estimate reflectivity series from broadband seismic reflection data and then translated to acoustic impedance, a process known as Maximum Likelihood seismic inversion.

Another type of seismic inversion employed in this study is the Model-based seismic inversion, which is quite popular in the geophysical world because it estimates acoustic impedance quickly and reliably. This method uses a forward modeling technique to generate synthetic seismic data based on an acoustic impedance model of the subsurface. This low impedance model is generated by interpolating well log impedance in the seismic section using the seismic horizon as a guide (Maurya et al. 2019; Kushwaha et al. 2021). Following that, an error between synthetic and real seismic data is estimated, and if the error is not small enough, the initial guess model is revised until the desired result is achieved. The minimization of error can be performed in the least square sense. Because the model-based inversion does not employ direct seismic data, the output is free of the noise component that is almost always present with seismic data (Mallick 1995; Maurya and Singh 2018).

The seismic frequency band is limited to about 15–80 Hz, and hence the low and high-frequency components are often missing for the inversion which is one concern during inversion. The non-uniqueness of the solution, which can lead to numerous potential geologic subsurface models that fit the data equally well, is the next major issue with seismic inversion (Russell 1988; Chambers and Yarus 2002). Furthermore, due to multiple reflections, transmission losses, geometric spreading, and frequency-dependent absorptions, the inversion approach suffers from noisy data (Bosch et al. 2010). To get more detailed, high resolution, and deeper information about the subsurface, one needs to reduce the above uncertainty as much as possible. One way to reduce these uncertainties uses some additional data which is derived from well log data. This well log data supply low as well as higher frequency components to the inversion. As a result, the final inversion findings are dependent on both the seismic data and the supplementary information acquired from the well log data (Mavko and Mukerji 1998; Ansari 2014). Before performing a seismic inversion, it's important to understand the geology of the area and other input parameters therefore well log analysis becomes a critical step to learn more about the subsurface at the well site.

Well log is one of the most fundamental tools for reservoir characterization in the oil and gas business, and it is an important way for geoscientists to learn more about the state under the surface. This approach is extremely effective for detecting hydrocarbon-bearing zones, calculating hydrocarbon volume, and a variety of other applications. Using well log data, the user may be able to determine shale volume (\({V}_{sh}\)), water saturation (\({S}_{w}\)), porosity (φ), permeability (k), elasticity (\(AI, SI\), etc.), reflectivity coefficient (\(R\)), and other data that the user requires (Crain 2006).

Well log data must be interpreted in various steps, and it is not advised that the user evaluate them at random because the result could be a complete error. Petrophysics (shale volume, water saturation, permeability, and other geology-like qualities) and rock physics (elasticity, wave velocity, and other geophysics-like properties) are the two types of properties that will be employed in reservoir characterization. Every property is linked to the others. The user can use RHOB-NPHI cross-over, reflectivity coefficient, and AI anomaly to determine a hydrocarbon-bearing zone (Minigaliev et al. 2018). Because each method has its flaws, it's a good idea to use all of them to get the best result. Furthermore, these well log analyses provide valuable information about the reservoir and fluid properties, but because wells are typically sparse, they are unable to provide information about the reservoir's horizontal extent in the subsurface. Several ways have been developed to address this issue, one of which being seismic inversion methods. To estimate the variation of impedance and characterize the anomalous zone, the technique is applied to a seismic section from the KG basin in India.

The study area

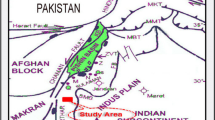
Well log from the Krishna Godavari basin along with the post-stack seismic data are used in the present study. The KG basin is a huge deltaic plain produced by two large east coast rivers, the Krishna and Godavari, in the state of Andhra Pradesh and the adjacent territories of the Bay of Bengal into which these rivers release their water. The Krishna Godavari basin is a confirmed continental margin petroliferous basin on India's east coast. The basin covers the land as well as the offshore area. Its on-land portion covers approximately 15,000 sq km area, while the offshore portion covers nearly 25,000 sq km along with up to 1000 m isobaths (Biswas 2003). The sediments in the basin are around 5 km thick, with multiple cycles of deposition dating from the late Carboniferous to the Pleistocene. The Krishna-Godavari basin has commercial hydrocarbon accumulations ranging from the earliest Permo-Triassic Mandapeta sandstone on land to the youngest Pleistocene channel levee complexes offshore. Because of their diverse tectonic and sedimentary properties, the basin has four petroleum systems, which can be grouped roughly into two categories: Pre-Trappean and Post-Trappean (Jain et al. 2012).

A typical rifted passive margin basin is the Krishna-Godavari basin. During the late Jurassic period, the basin developed over the Eastern Ghat tectonic grain as a result of Indo-Antarctica plate separation and the influence of oblique extension (Rao 2001). The pericratonic Krishna Godavari basin overlies orthogonally the southern extension of the intracratonic Pranhita–Godavari (PG) paleo rift in the northeastern region of the basin, resulting in a dual rift province of basin evolution with typical tectonic-sedimentary assemblages (Biswas 2003). The Krishna Godavari pericratonic basin is characterized by northeast-southwest trending tectonic highs and lows, as well as a sequence of intrabasinal ridges (Fig. 1), including Bapatal, Kaza Kaikular, Tanuku, and Poduru-Yanam (from northwest to southeast). The subsurface geology represented in the NW–SE geological segment confirms the PG graben's continuity over the Gudivada and Mandapeta grabens' north eastern halves. From the Permian to the Recent, tectono-sedimentation events have left their mark on the KG Basin (Shankar and Riedel 2010).

Fig. 1
figure 1

Location of the study area, KG basin, India (left), and basin architecture along with petroleum system (right)

Full size image

The KG basin is divided into three sub-basins namely Krishna, West Godavari, and East Godavari, which are separated by the Bapatla and Tanuku horsts (Fig. 1), respectively. The reservoir rocks in this basin are predominantly sandstone, shaly sandstone, siltstone, and sandy siltstone, with hydrocarbon buildup expected in a variety of traps such as anticlines, faults, unconformities, lenses, pinch-outs, or combinations of these (Satyavani et al. 2016). Non-traditional stratigraphic traps such as channel fill, regional sand pinch-outs, and truncations are thought to be prominent hydrocarbon accumulators (Gupta 2006; Shanmugam et al. 2009).

The Eastern Ghats' Precambrian igneous and metamorphic complex serves as the KG basin's foundation. The presence of linear subsurface basement highs and lows is indicated by the primary tectonic features detected with the use of 2 Composite Bouguer Anomaly maps, a Residual Gravity map, and seismic data. The Krishna, West Godavari, and East Godavari depressions are separated by basement highs known as the Baptala and Tanuku ridges in the KG basin (Arsalan and Yadav 2009). The main Godavari basinal area is defined by the significant cross trends of Pithpuram and Chintalapudi. The West Godavari is divided by the Chintalapudi cross trend into the Bhimadolu depression to the north and the Gudivada and Bantumali depressions to the south, separated by the Kaza ridge. Over the ridges, the average thickness of the sediments varies from 0.5 km on the Baptala ridge to 2.5 km on the Tanuku ridge. The thickness of the depressions varies from 3 km in the Krishna depression to nearly 7 km in the Godavari depression (Shankar and Riedel 2010; Ghosh et al. 2010).

Several gas fields, mainly in the East Godavari Sub-Basin, are generating from Paleocene reservoirs. On land, the Tatipaka, Pasarlapudi, Kadali, and Manepalli fields are located, while GS-8 is located offshore in the basin. On the basinal side, the hydrocarbon generation centers in the Paleocene show fair to abundant organic composition. The presence of gas and its pressure in this sequence support Paleocene potential in the basin. In this age category, ten hydrocarbon pools have already been found. The Eocene gas accumulation can be seen in Elamanchili, Tatipaka, and Pasarlapudi, among other places. Oil is produced in the Mori prospect (Riedel et al. 2010). These oil fields, notably GS-38 in the offshore area, show that the Eocene sequence has good hydrocarbon potential. Eocene hydrocarbon generation centers In the lower deltaic portions of the Godavari river and shallow seas of Masulipatnam Bay, reefal limestone and accompanying shelf sediments of Eocene age offer another category of hydrocarbon plays. Oil and gas entrapment could be possible in drape folds on a slanted narrow fault block. There have already been eight hydrocarbon pools found (Rao 2001; Ghosh et al. 2010). Figure 1 depicts the research area's location.

In the present study, processed post-stack seismic reflection data is utilized for the analysis. Processing of data has been done in three phases, in the first phase; pre-stack signal processing has been performed. Further, in the second phase pre-stack time migration has been done followed by post-stack signal processing in the third phase. The details of the processing sequence are given as follows.

Phase 1: Pre-stack signal processing

  • SEGY to internal format conversion, resampling data from 2 to 4 ms with antialias filter

  • T2 spherical compensation

  • Front mute and broad pre-filtering (8–90 Hz)

  • Spike deconvolution (4 ms PDL) with 480 ms OPL and 1% whitening

  • Post-deconvolution broad band filtering (8–90 Hz)

Brute stack Phase-2: Pre-stack time migration

  • 2 km interval velocity analysis

  • NMO correction and stack

  • FK multiple attenuation

  • Offset regularization, uniforming fold to 35 by partial stack

  • Inverse NMO on uniformed CMP gathers

  • Flat event velocity analysis for DMO at locations identified on stack section

  • Apply NMO correction using velocity field build from flat event velocity functions

  • Cascaded Stolt pre-stack time migration on common offset planes

  • Sorting common offset datasets to CRP gathers

  • Inverse NMO and velocity analysis at 1 km interval

  • NMO correction to the pre-stack migrated CRP gathers, optimal mute and stack

  • Inverse migration

Phase 3: Post-stack signal processing

  • Spike deconvolution with 4 ms predictive distance and 480 ms operator length

  • FX deconvolution

  • Time variant band pass filtering

  • Omega-X post-stack time migration

  • 500 ms AGC

The research is organized into three sections. The first is a well log analysis to evaluate reservoir and fluid parameters. Then, to estimate acoustic impedance and interpret for the reservoir, maximum likelihood seismic inversion (MLSI) is used. Finally, model-based seismic inversion is used to estimate acoustic impedance, and the findings are compared to those obtained using the maximum likelihood approach. The approach for these methods is given in-depth in the following sections.

Well log analysis

The well log data was obtained from the KG basin east coast of India was analyzed and discussed in this section. The petrophysical analysis of drilled targets in wells which includes the vertical distribution of petrophysical parameters, lithological interpretations from parameter cross plots serves as the basis for determining oil and gas potentiality in reservoirs (Singh et al. 2020). The available log data for the studied units include gamma-ray, neutron porosity, bulk density, resistivity, and sonic. The determination of the amount of shale present in the formation is an essential step in the formation evolution process. (Opuwari 2010; Ulasi et al. 2012). The volume of shale is calculated using gamma-ray log, density porosity is calculated from density log and \({V}_{P}/{V}_{S}\) the ratio is calculated from the sonic log are the various petrophysical parameters that were evaluated. Low gamma-ray value, low density, high resistivity, and the crossover in the neutron–density log show the presence of a hydrocarbon-bearing zone. Three zones are identified in between (1918–1960 m, 2116–2136 m, and at the depth range of 2221–2245 m). The detailed well log analysis is performed in the given three zones. Water saturation is calculated which led to the estimation of hydrocarbon saturation. The bulk volume of water is also calculated within three zones of interest. Movable oil saturation and movable hydrocarbon index are also calculated and presented in Table 1. Furthermore, Figs. 2 and 3 show plots of different petrophysical parameters along with recorded well logs against depth, and three zones are highlighted by a rectangle.

Table 1 Reservoir properties calculated for different reservoir zones.(GR = Gamma Ray, Vsh = Shale volume, Resi = Resistivity, PHID = density porosity, PHIE = effective porosity, Sw = water saturation, Sh = hydrocarbon saturation, BVW = Bulk volume water, ROS = residual oil saturation, MOS = movable oil saturation, MHI = Movable hydrocarbon index)
Full size table
Fig. 2
figure 2

The plot of Gamma-ray, Density, resistivity, Water saturation, Phid/Nphi and velocity along with depth. Anomalous zones are highlighted by the rectangle

Full size image
Fig. 3
figure 3

The plot of Shear modulus, young modulus, bulk modulus, Vp/Vs, poisson’s ratio and shale volume against depth. Anomalous zones are highlighted by the rectangle

Full size image

The lithological content of the KG basin is investigated using different cross-plots such as density and P-impedance, Density and Neutron, Sonic and Density logs, etc. Figure 4 presents three types of cross plot, in which Fig. 4a shows density and P-impedance cross plot, Fig. 4b shows poison’s ratio and lambda rho cross-plot and Fig. 4c depicts \({V}_{P}/{V}_{S}\) and P-impedance cross plot. In the cross plot between density and P-impedance, the low value of density and P-impedance indicates the presence of hydrocarbon. Similarly, the low value of Poisson’s ratio and Lambda rho in the cross plot indicates the presence of hydrocarbon. Further, \({V}_{P}/{V}_{S}\) ratio plays an important role in the identification of fluid content and lithology. \({V}_{P}\) is affected by the compressibility of fluid in the rock but it hardly influences \({V}_{S}\). \({V}_{P}/{V}_{S}\) is an excellent indicator of pore fluid. In Fig. 4c, \({V}_{P}/{V}_{S}\) is low, indicates the presence of gas reservoir and its values lie in the range of 1.6–1.7.

Fig. 4
figure 4

Cross plot between a density and P-impedance, b Poisson’s ratio and Lambda rho, and c \({V}_{P}/{V}_{S}\) and P-impedance

Full size image

Further, the density neutron cross plot is one of the approaches available for porosity log analysis. A cross plot method called the shaly-sand model is commonly used. This model, on the other hand, is regarded as a poor fit for any sandstone that contains minerals other than quartz. In quartz sands, the complex lithology model performs well and is recommended model for study (Ulasi et al. 2012). The density neutron cross plot is presented in Fig. 5a and the three solid lines in the cross plot indicate sandstone, dolomite, and limestone lithology. Figure 5a shows the cross plot for the entire depth whereas zone A is shown in Fig. 5b. From the figures (Fig. 5a, b) show the points are scattered in between sandstone and dolomite and indicate that the reservoir zone is dominated by sandstone lithology.

Fig. 5
figure 5

Cross plot of density versus neutron porosity for (a) entire depth, b zone A (1918-1960 m), the cross plot of sonic and neutron log c) for entire depth, d) for zone A (1918-1960 m), sonic and neutron cross plot for the reservoir zone B (2116-2136 m) and f,) depicts sonic neutron crossplot for zone C (2221-2245 m)

Full size image

In the case where the density-neutron method is not applicable, the sonic-neutron cross plot model is used to determine the porosity. In the area where the shale volume, matrix rock properties, and sonic compaction effects are all known then the method works well. The shale corrected density neutron complex lithology cross plot method is a superior model that does not require matrix rock parameters if both density and neutron log is available (Maurya et al. 2020). Figures 5c–f show a cross plot between the sonic log and neutron porosity log for the entire zone, zone 1, zone 2, and zone 3 respectively. In these figures, three solid lines are plotted which represent sandstone, dolomite, and limestone lithology. Above these plots, the well log data of sonic and neutron log is plotted for the entire zone, zone 1, zone 2 zones 3 in fig. 5c–f respectively. From Fig. 5c, most of the scatter points lie near the sandstone line, and a few points lie in between limestone and dolomite again indicate the major lithology of the study area is sandstone. Figure 5d shows the cross plot for zone A (1918-1960 m) in which the points lie in the sandstone line depicts that the reservoir is mainly composed of sandstone. Figure 5e shows the cross plot for zone B (2116-2136 m), the scatter points lie mainly on the sandstone line. Similarly, Fig. 5f shows the cross plot for zone C (2221-2245 m), and the scatter points lie in between sandstone and limestone.

Reservoir characterization considers the elastic properties such as velocity, density, impedance, and VP/VS ratio andto analyze these elastic properties, rock physics acts as a link betweenthe elastic properties and the reservoir properties such as water saturation, porosity, and shale volume. In this study, we build up a rock physics template and plot it along with the inverted elastic properties to aid the efficient interpretation. Petrophysical properties, fluids can be related to reservoir using RPT as a tool. We have studied the fluid sensitivity of petrophysical properties based on the experimental data by calculating fluid indicators and using cross-plots. The ratio of compressional and shear wave velocity versus acoustic impedance as rock physics template for KG Basin has been derived for siliciclastic rocks based on formation evaluation of well-log data studies showed that RPTs, built with acoustic impedance and P- to S-wave velocity ratio, serve as tools for lithology and fluid identification (Chi and Han 2009; Datta Gupta et al. 2012; Ba et al. 2013).The result is a rock physics template which includes important properties such as porosity, true vertical depth and fluid type from log data and which is considered useable throughout different areas and various lithology of the KG Basin (Fig. 6). The idea was to create basin and lithology-dependent templates mainly with elastic properties of rocks (most commonly the ratio of compressional and shear wave velocity (\({V}_{P}/{V}_{S}\)) and acoustic impedance (AI) of rocks. These templates, which are able to indicate fluid and lithology trends, can then be used for interpretation of seismic data from the corresponding basin or lithology. Figure 7 shows plot of clustering (left) in which three types of lithology are identified and on the right side shows cross-section of impedance and \({V}_{P}/{V}_{S}\) ratio in which three lithology is shown vertically.

Fig. 6
figure 6

Figure shows Vp/Vs versus AI crossplot from well depicts porosity percentage of gas sand and shale formation

Full size image
Fig. 7
figure 7

Figure shows automatic clustering using statistical K-means and found 3 clusters based on data distribution areas

Full size image

Maximum likelihood inversion

One of the methods used to determine petrophysical parameters in the inter-well zone is maximum likelihood seismic inversion. It's a type of post-stack seismic inversion method that uses post-stack seismic data as input to calculate subsurface acoustic impedance. It stimulates a seismic trace that models subsurface reflectivity with the fewest possible acoustic impedance interconnections. It is based on the notion that the earth's acoustic impedance reflection coefficient series is sparse. This approach employs the L2-norm solution for its implementation, which is based on error minimization (Russell 1988; Zhang and Castagna 2011).

In two steps, the greatest likelihood inversion is carried out. The seismic reflectivity series is estimated in the first step using the maximum likelihood deconvolution method. The reflectivity series is then converted into the acoustic impedance in the second stage, which is more essential for inferring data about the subsurface layer (Sacchi and Ulrych 1995; Maurya and Singh 2019).

The basic theory of maximum likelihood deconvolution (MLD) was developed by Dr. Jerry Mendel and his associates at USC and has been well publicized (Kormylo and Mendel 1983; Chi et al. 1984). The fundamental assumption of maximum likelihood deconvolution is that the earth’s reflectivity is composed of a series of large events superimposed over small spikes in the background. This method gives estimates of both the sparse reflectivity and wavelet. Geologically, the large events correspond to unconformities and major lithological boundaries (Maurya and Singh 2018). To get the solution, one needs to optimize the objective function which can be written for reflectivity and noise as follows.

$$ E = \mathop \sum \limits_{k = 1}^{L} \frac{{r_{{\text{k}}}^{2} }}{{R^{2} }} + \mathop \sum \limits_{k = 1}^{L} \frac{{n_{k}^{2} }}{{N^{2} }} - 2m {\text{ln}}\left( \lambda \right) - 2\left( {L - m} \right){\text{ln}}\left( {1 - \lambda } \right) $$
(1)

where \({r}_{k}\) the reflection coefficient at the kth sample, m is the number of reflections, L is the total number of samples, N is the square root of noise variance, nk is the noise at the kth sample, and \(\lambda \) is the likelihood that a given sample has a reflection.

After solving the objective function (Eq. 1) using L2 norm methods, we will have earth reflectivity series which can be converted into impedance which is more correlated with geology as compared with reflectivity. This can be achieved using two approaches which are discussed in the following sections.

  1. 1.

    The first approach is that the acoustic impedance can be estimated by using the direct relationship between reflectivity and impedance.

    $$ Z_{{\text{j + 1}}} = Z_{{\text{j}}} \mathop \prod \limits_{k = 1}^{{\text{j}}} \left( {\frac{{1 + r_{{\text{k}}} }}{{1 - r_{{\text{k}}} }}} \right) $$
    (2)

    It is noticed that the first approach is not able to model completely reflectivity series into impedance as the relationship does not include any noise component which is obvious by considering real seismic data.

  2. 2.

    The second approach can model acoustic impedance from the reflectivity series using the following relationship.

    $$ \ln (Z_{i} ) = 2H\left( i \right)*r\left( i \right) + n\left( i \right) $$
    (3)

where

$$ H\left( i \right) = ~\left\{ {\begin{array}{*{20}c} {1,~~~~if~i < 0} \\ {0,~~~~if~i > 0} \\ \end{array} } \right. $$

\({Z}_{i}\) is known as impedance trend, \(r(i)\) is the earth reflectivity series and \(n(i)\) is the noise component in the input trend.

Application to real data

Post-stack seismic data from KG Basin along with one well log KG_D6_A5 are utilized to extract subsurface acoustic impedance using maximum likelihood inversion methods. The big challenge before performing seismic inversion is time to depth conversion. This is important because during the inversion process, we are going to utilize seismic and well log data together and both data sets are generally in a different domain, seismic data is in the time domain and well log data is in-depth domain and hence needs to convert depth into time. This becomes an easier job if check shot data is available which can be directly used to convert depth into time. No check shot information has been provided from the KG basin hence some alternative technique needs to be adopted. In this study a manual technique is used for conversion and processes are as follows.

  1. 1.

    Extract wavelet from seismic data

  2. 2.

    Calculate reflectivity from well log data using modified Eq. 2.

  3. 3.

    Convolve wavelet with reflectivity to get synthetic trace using Eq. 4.

  4. 4.

    Compare generated synthetic with real seismic trace near to well location.

  5. 5.

    Stretch and squeeze synthetic trace to match with real seismic trace

  6. 6.

    The moment at which the exact match will occur provides depth to time relation (Maurya et al. 2020).

After time to depth conversion, seismic analysis is performed. To optimize inversion parameters, first, on single seismic trace near to well location is extracted and inverted. As the seismic trace is very close to the well log data, therefore, the extracted seismic trace and well log have the same lithology. A comparison of well log impedance with inverted impedance is displayed in Fig. 8. The first column of Fig. 8 compares inverted and well log impedance, the second column shows the error between inverted and well log impedance, the third column depicts extracted wavelet, the fourth and fifth column shows synthetic and seismic trace respectively and the sixth column shows the error between synthetic and seismic trace. Column 1 of Fig. 8 contains 3 curves, the black solid line is our initial impedance model, the blue line shows well log impedance and the red line depicts inverted impedance. From the figure, one can notice that the inverted impedance is following a trend with well log impedance. The correlation between inverted and real impedance is achieved to be 0.936 which indicates good results. The RMS error between synthetic and real seismic data is found to be 0.35 which is quite low and again support good result.

Fig. 8
figure 8

Shows inversion analysis results for composite trace. The first track shows a comparison of inverted (using maximum likelihood inversion) and original impedance with the initial model, the second track shows the error between original and inverted impedance, track 3 depict extracted wavelet, track 4 shows synthetic traces, track 5 depicts seismic reflection data and track 6 shows RMS error between synthetic and seismic traces

Full size image

A cross plot between inverted impedance and well log impedance is also generated and shown in Fig. 9. This figure is generated to compare sample by sample inverted and well log impedance. The figure indicates again good inversion results as most of the points lie near to best fit line.

Fig. 9
figure 9

Cross plot between inverted (derived using Maximum likelihood) and original impedance from well logs

Full size image

At this point, we are in a position to invert the entire 2D post-stack seismic data into acoustic impedance. The maximum likelihood technique is applied to the data and finally, acoustic impedances are estimated in the inter-well region and one section of results is displayed in Fig. 10. The inverted section shows very high-resolution subsurface information as compared to the seismic section. From the Fig. 10, two low impedance zone is identified which indicate the presence of loose (sand) formation in this zone. It is also noticed that the loose formation is covered by very high impedance (hard rock) which creates a favorable condition for the presence of hydrocarbon.

Fig. 10
figure 10

Cross-section of inverted impedance estimated using Maximum Likelihood inversion technique

Full size image

Model-based seismic inversion

Model-based seismic inversion is a post-stack seismic inversion approach that inverts post-stack seismic data into acoustic impedance and is widely utilized in geosciences. The method is based on the convolutionary principle, which asserts that a seismic trace can be formed by the convolution of a wavelet with the earth's reflectivity series plus noise (Mallick 1995). It can be stated mathematically as follows.

$$ S\left( t \right) = \left[ {W\left( t \right)*R\left( t \right)} \right] + N\left( t \right) $$
(4)

where \(S(t)\) represents the seismic trace, \(W(t)\) seismic wavelet, \(R(t)\) reflectivity, \(*\) represents the convolution operator, and \(N(t)\) is the noise component in the data.

The noise component in Eq. 4 is uncorrelated with the seismic signal hence the equation can be solved for earth reflectivity by iteration process. (Latimer et al. 2000; Leite 2010). This type of problem is known as non-linear and can be solved iteratively as follows.

If one knows the velocity (V) and density (\(\rho \)) of the layers, one can calculate the impedance (Z) of that layer as follows.

$$ Z = \rho *V $$
(5)

Further, if one knows the impedance of layers, the earth’s reflectivity series can be extracted as follows.

$$ R_{i} = \frac{{Z_{i + 1} - Z_{i} }}{{Z_{i + 1} + Z_{i} }} $$
(6)

where \({Z}_{i+1}\) and \({Z}_{i}\) are the impedance of (i + 1)th and ith layer and \({R}_{i}\) is the reflectivity of the ith interface.

Thereafter, the acoustic impedance (AI) of the nth layer can be calculated using the following equation.

$$ AI_{N} = AI_{1} exp\left( {\mathop \sum \limits_{i = 1}^{n} R_{i} } \right) $$
(7)

where \({AI}_{1}\) is the acoustic impedance of the first layer and \({AI}_{N}\) is the acoustic impedance of the Nth layer. Equation 7 is valid for \({R}_{j}\le |0.3|\) case only. The workflow of the model-based inversion method is given in Fig. 11 (Berteussen and Ursin 1983; Ferguson and Margrave 1996).

Fig. 11
figure 11

Flowchart of model-based seismic inversion methods adopted in this study

Full size image

Application to real data

Similar to the maximum likelihood methods, depth to time conversion was performed as discussed in Sect. 4 and a single seismic trace is extracted near to well location to optimize model-based inversion parameters. Inversion is performed on extracted trace and compared it with well log impedance. The result of the composite trace is displayed in Fig. 12. From the figure, one can notice that the inverted impedance is following a trend with the actual impedance from well log data. In both the cases (maximum likelihood and model-based) the exact match between inverted impedance and actual impedance from well log data is not accurate. The reason behind this misfit is that the frequency content of these two datasets. The well log data has a frequency range from 0 to 120 Hz whereas seismic data has a frequency range from 10 to 80 Hz. The seismic data lack low as well as a high-frequency component as compared with well log data.

Fig. 12
figure 12

Shows inversion analysis results for composite trace. The first track shows a comparison of inverted (using model-based inversion) and original impedance with the initial model, the second track shows the error between original and inverted impedance, track 3 depict extracted wavelet, track 4 shows synthetic traces, track 5 depicts seismic reflection data and track 6 shows RMS error between synthetic and seismic traces

Full size image

Cross plots between inverted impedance and well log impedance are also generated and shown in Fig. 13. A best-fit line is plotted in the cross plot and found most of the scatter points are near to this best fit line. The scatter points show that the inverted results are very close to the real impedance from well log data and indicate good results of model-based inversion methods. The analysis also reveals that the correlation coefficient between inverted and real impedance is 0.97 and the RMS error is 0.259 which again indicates a good inversion result.

Fig. 13
figure 13

Cross plot between inverted impedance from model-based inversion and original impedance from well log data

Full size image

Now we are moving towards the inversion of entire 2D post-stack seismic data to extract acoustic impedance which is more meaningful as compared with the seismic data. The entire data is inverted for acoustic impedance and one section is presented in Fig. 14. From the figure (Fig. 14), one can notice that the inverted results show a very high-resolution picture of the subsurface as compared to the original seismic data recorded at the surface. This is the beauty of seismic inversion to extract more meaningful information from less informative seismic data. The area shows impedance variation from 1800 m/s*g/cc to 10000 m/s*g/cc which indicate the presence of loose formation in some part of the study area and can be recognized by green color in Fig. 14. The figure shows two anomalous zones with very low acoustic impedance and is highlighted by arrow and ellipse in Fig. 14.

Fig. 14
figure 14

Cross-section of inverted impedance estimated using Model-based inversion technique

Full size image

Discussions

Well log analysis is carried out from the data available on the KG basin, India. The log response shows low gamma value, high resistivity, and crossover between neutron and density porosity indicate the presence of a hydrocarbon-bearing zone. Three zones were identified at the depth of (1918–1960 m), (2116–2136 m), and (2221–2245 m) to justify it, various petrophysical parameters were evaluated and shown in Table 1. Average effective porosity is found to be 15%, 15%, and 14% in the three zones respectively, water saturation is low conversely hydrocarbon saturation is found to be high in all three zones. Thereafter, different cross-plot techniques are used such as Density vs P-impedance, Poisson ratio vs Lambda rho, \({V}_{P}/{V}_{S}\) vs P-impedance etc. This crossplot is useful for lithological and fluid identification. From \({V}_{P}/{V}_{S}\) vs P-impedance cross-plot,\({V}_{P}/{V}_{S}\) value is found to be low implies the presence of gas in all three zones. In the density vs P-impedance cross-plot, both values are low indicating the presence of hydrocarbon. For lithology identification neutron – density and sonic –neutron cross plots are plotted which indicate that the formation is mainly of sandstone with some limestone intercalations. Sonic-density cross plot mainly indicates the presence of dolomite but since the spacing between the three rock lines is too small so it cannot be taken further for the analysis. Some important parameters such as bulk volume water, movable oil saturation, and movable hydrocarbon are also calculated and all the values are found to be in favor of hydrocarbon presence.

Thereafter, two types of seismic inversion namely maximum likelihood and model-based seismic inversion are performed in this study and subsurface acoustic impedance is extracted. The objective was to delineate subsurface lithology and find the lateral and vertical extent of the sandstone formation. In these two seismic inversion methods, the model-based seismic inversion is very famous and can be used in all types of geophysical data sets. On the other hand maximum likelihood, seismic inversion is not as much famous as model-based although the methods are not very new. The reason behind this is the performance of maximum likelihood seismic inversion methods largely depends on seismic data and hence researchers avoid it as the method needs to be tested. Here we utilized maximum likelihood methods as an alternative seismic inversion technique and compared both model-based inverted results and maximum likelihood inverted results.

Figure 15 compares correlation coefficient and RMS error estimated in both model-based and maximum likelihood seismic inversion methods. From the figure, one can notice the correlation coefficient is slightly better in model-based inversion methods as compared with maximum likelihood methods. The RMS error is low for model-based inversion as compared to the maximum likelihood methods.

Fig. 15
figure 15

Comparison of correlation coefficient and RMS error of Model-based inversion and maximum likelihood inversion

Full size image

Further, very important parameters called amplitude variation with frequency i.e. amplitude spectrums are compared among seismic data (Blue line), inverted synthetic from model-based (Red line), and inverted synthetic from maximum likelihood (Black line) and shown in Fig. 16. From Fig. 16, one can notice that model-based and maximum likelihood curves follow the trend of original seismic data very well. The model-based amplitude curve deviates more as compared to the maximum likelihood amplitude curve which indicates that the amplitude of model-based inversion results are not accurately matching with real seismic data whereas the amplitude spectrum of maximum likelihood inverted results are more close and hence depicts that the inverted results are closer to the real subsurface mode.

Fig. 16
figure 16

Comparison of the amplitude spectrum of Maximum likelihood inverted synthetic, model-based inverted synthetic and real seismic data

Full size image

A difference between inverted impedance from model-based inversion and maximum likelihood inversion is generated (Fig. 17) to see the major changes in both the section. From the figure, one can notice that the impedance differences between two section vary from nearly -2000 m/s*g/cc to + 2000 m/s*g/cc which indicate that in some area maximum likelihood is better and another area model-based inversion is better. The red and pink color shows the greatest difference between the two results. Figure 17 also indicates that the presence of a higher impedance section zone has a large difference between Model-based and maximum likelihood whereas the lower impedance zone has the least difference. This can be interpreted that the low impedance area, both methods (model-based and maximum likelihood) have no much difference whereas the high impedance area, both methods need to be more careful before their application.

Fig. 17
figure 17

Difference between impedance contrasts estimated using model-based inversion and maximum likelihood inversion

Full size image

The inverted impedance synthetic from model-based inversion and maximum likelihood inversion against real seismic section is cross-plotted and shown in Fig. 18. Figure 18a shows a cross plot of model-based inverted synthetic with seismic data at horizon 2 with a 100 ms time interval. The distribution of scatter points indicates decent results as most of the points lie close to the best fit line and indicate less difference between real seismic and inverted synthetic sections. On the other hand, the cross-plot between maximum-likelihood inverted synthetic section and real seismic section at near horizon 2 with 100 ms window indicates little scatter points as compared with model-based inversion case and depicts slightly difference between real seismic and inverted synthetic section (Fig. 18b). Although most of the data points are as close as it was found in the case of model-based inversion.

Fig. 18
figure 18

Cross plot of seismic reflection and a inverted model-based synthetic and b inverted maximum likelihood-based synthetic

Full size image

Conclusions

In this study well log analysis and seismic inversion techniques are applied to the post-stack seismic along with well log data from the Krishna Godavari basin, India to extract subsurface rock and fluid properties. The log response from the well shows low gamma value, high resistivity, and crossover between neutron and density porosity indicated the presence of hydrocarbon-bearing three zones. These three zones are at the depth of (1918–1960 m), (2116–2136 m), and (2221–2245 m). Average porosity is found to be 33%, 36%, and 37% in the three zones whereas water saturation is low conversely hydrocarbon saturation is found to be high in all three-zone. Thereafter, different cross-plot techniques are used for lithological and fluid identification. These crossplot and other analyses confirm that all three anomalous zones contain gas as a hydrocarbon. Further, the study also reveals that the formation is mainly composed of sandstone with some limestone intercalations. Thereafter, two types of seismic inversion techniques viz. model-based seismic inversion and maximum likelihood inversions are employed and subsurface acoustic impedances are estimated. Both methods can extract very high-resolution subsurface acoustic impedance and two anomalous zones are identified in both the results. These anomalous zones are found near 2350 ms and 2430 ms two-way travel time. These anomalous zones may be from the same which is interpreted from well log data but for confirmation some other parameters need to be tested. Comparison of both inversion methods reveals that the model-based inversion is slightly performing better as compared with maximum likelihood inversion. But the frequency content in maximum likelihood inverted results are more close to the real seismic data as compared with the model-based inverted results particularly in the lower frequency range (< 50 Hz). The high impedance zone in the subsurface shows much deviation between model-based derived and maximum likelihood derived results whereas the low impedance zone is retrieved similarly in both methods. The analysis also concluded that in the low impedance area any one of both (model-based and maximum likelihood) methods can be used whereas in the high impedance area one needs extra precautions before application of any of these methods.