Introduction

Shale is basically defined as a clay-rich non-clastic sedimentary rock, which primarily comprises silts, clays and mud in varying proportions (Gholami et al. 2018). In general, these formations are utterly responsible for causing over 70% of the wellbore instability problems (Gholami et al. 2018; Aftab et al. 2017). The instability problems mainly arise by the presence of clay minerals in the shale formation (Aftab et al. 2017; Lal 1999). These clay minerals are classified into three distinct categories, namely kaolinite, montmorillonite and illite (Aftab et al. 2017 , 2017; Lal 1999). Out of these three categories, montmorillonite demonstrates strong affinity to water, as swelling starts to occur once the rock fluid interaction is established (Khodja et al. 2010; Salles et al. 2008). This clay mineral tends to swell up to ten times of its original size with the migration of water molecules and hence results in various wellbore instabilities issues (Fink 2012). The movement of the water molecules inside the shale structure occurs either by crystalline process or by osmotic patterns. The former is considered to be insignificant during drilling operations, and it normally occurs in all kinds of clay minerals. On the other hand, osmotic swelling is generally responsible for causing a considerable increase in the volume of the shale rock (Fink 2012). The difference in concentration of the cations that are present in clay mineral and surrounding water gives rise to different forces that are eventually the main source of this type of swelling (Oort 2003; Nehdi 2014; Hashmi et al. 2012).

The forces that are acting on the shale rock are subdivided into two categories, namely mechanical and physicochemical (Oort 2003). The latter forces are supramolecular interactions comprising Van der Waals force of attraction, ionic interactions, hydrogen bonding, π–π conjugation, born repulsive forces and short-range forces of attraction and repulsion that are formed by the hydration of clay surfaces (Oort 2003; Vatankhah-Varnoosfaderani et al. 2015, 2014, 2017; GhavamiNejad et al. 2014). Such forces are essentially responsible for the swelling behavior of the clay minerals. This swelling characteristic of the clay mineral in the shale is similar in behavior to the superabsorbent hydrogels (Vatankhah-Varnoosfaderani et al. 2015, 2014; GhavamiNejad et al. 2016). The hydrophilic nature of these gels not only allows them to absorb large quantity of aqueous solution, but it also ensures that the solution retains there for a longer time (Bertling and Bertling 2007; Kabiri et al. 2003aa2). This behavior is also there in clay minerals, where water adsorption activity is extremely high that eventually causes severe wellbore instability issues.

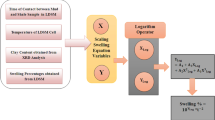
For a particular adsorption system, it is extremely imperative to take into the account the adsorption kinetics as it helps in comprehending the mechanisms involved in a particular adsorption process (Guo and Wang 2019). Several empirical kinetics models such as Peleg’s, first-order exponential association equation and pseudo-second-order kinetics are there in the literature that define the adsorption kinetics for a specific adsorption system. These models are considered to be relatively accurate analytical tools for modeling of adsorption kinetics. The Peleg’s non-exponential model is widely used for the modeling of hydration characteristics of different food materials (Igathinathane et al. 2009; Cunningham et al. 2007). It was further used to model the absorption of water on the surface of the grains (Kipcak et al. 2014). While, the first-order kinetics model was proposed by Lagergen by the end of the nineteenth century (Simonin 2016). In the literature, this model is also used to model adsorption kinetics of a system having different adsorbate concentrations (Guo and Wang 2019; Azizian 2004). Similarly, pseudo-second-order kinetics became popular in 1999 when Ho and co-workers performed various experiments and concluded this model as the best in correlating the experimental results (Simonin 2016; Ho 2006). The swelling of a shale formation exhibits a similar trend as shown by these models while used in different industrial sectors. The graph obtained from linear dynamic swell meter (LDSM) is similar in shape to the sorption rate characteristics curve for different foodstuff. Moreover, apart from these kinetic models a scaling swelling model was also developed in 2021 by the author’s group that is also analyzed in this study. This model uses a third-degree polynomial equation for modeling of shale swelling response obtained from linear dynamic swell meter. The model comprises all the governing factors that are part of LDSM, which includes clay content, temperature, swelling percentages and time of contact.

The purpose of this study is to investigate in detail using graphical and statistical approaches through already established kinetic and scaling swelling models for the validation of the shale swelling experimental results obtained from LDSM. Prediction of an appropriate swelling model to probe the swelling behavior of such mineral-containing shale is the primary objective of this work. Additionally, the accuracies of all the models are analyzed and compared using different error analyses techniques. Furthermore, these comparative analyses give a detailed inside view on how the swelling occurs and which particular model best describes the swelling behavior of a shale sample.

Kinetic models applied in this study

Peleg’s model

It is basically defined as a two-parameter non-exponential model originated in 1988 by Peleg. This model was used for the absorption of water molecules over grains in food materials (Peleg 1988; Resio et al. 2006). Equation (1) shows Peleg’s model relationship.

$$S\left(t\right)= {S}_{\mathrm{o}}+\frac{t}{{k}_{1}+{k}_{2}t}$$
(1)

where \({k}_{1}\) and \({k}_{2}\) are denoted as characteristics constants and are inversely proportional to initial water absorption rate and equilibrium moisture content, respectively. \(S\left(t\right) and {S}_{o}\) are defined as the swelling at time (t) and swelling at equilibrium condition, respectively. The nature of the above equation is already defined in the form of a curve fitting model.

1st First-order exponential association equation

Lagergen proposed the first-order kinetic equation back in 1898 (Simonin 2016). Kinetic processes that are normally associated with non-equilibrium conditions are frequently described using this model (Guo and Wang 2019). Equation (2) displays the differential form of first-order kinetic equation (Guo and Wang 2019; Wang and Zhuang 2017; Hashmi et al. 2019). Integrating Eq. (2) by using the initial condition parameters yields the exponential form of first-order kinetic equation, which can be rewritten as Eq. (3). Furthermore, Mackay and Ho proposed the linear relationship for this model as denoted by Eq. (4), which is in the form of an equation of straight line yielding the slope that is equal to \({k}_{1}\).

$$\frac{\mathrm{d}{S}_{t}}{\mathrm{d}t}= {k}_{1}\left({\mathrm{S}}_{\mathrm{e}}-{\mathrm{S}}_{\mathrm{t}}\right)$$
(2)
$${S}_{t}= {S}_{e}(1-{\mathrm{e}}^{-{\mathrm{k}}_{1}\mathrm{t}})$$
(3)
$$\mathrm{ln}({\mathrm{S}}_{\mathrm{e}}-\mathrm{S}\left(\mathrm{t}\right))=\mathrm{ ln}{(\mathrm{S}}_{\mathrm{e}})- {\mathrm{k}}_{1}\mathrm{t}$$
(4)

where \({S}_{e}\), \({S}_{t}\) and \({k}_{1}\) are defined as swelling content at equilibrium, swelling content at time (t) and swelling kinetic constant, respectively (Kipcak et al. 2014).

Pseudo-second-order kinetics

Pseudo-second-order kinetics model is widely used in the adsorption process. Equation (5) describes the relationship for this model (Guo and Wang 2019; Yousef et al. 2020; Ho et al. 1996). By integrating Eq. (5) at initial condition, pseudo-second-order equation can be rewritten as shown in Eq. (6) (Guo and Wang 2019; Simonin 2016). This model defines the dependency of the adsorption process for a particular adsorbent on time (Edet and Ifelebuegu 2020). In terms of linear model \(y=at+b\), Eq. (6) can be transformed into Eq. (7). Here, \(a=\frac{1}{{\mathrm{q}}_{\mathrm{e}}} and b= \frac{1}{{\mathrm{k}}_{2}{{\mathrm{q}}_{\mathrm{e}}}^{2}}\)

$$\frac{\mathrm{d}{q}_{t}}{\mathrm{d}t}= {k}_{2}{({q}_{e}-{q}_{t})}^{2}$$
(5)
$${q}_{t}= {q}_{e}\frac{{{{q}_{e}}^{2}k}_{2}t}{1+{\mathrm{q}}_{\mathrm{e}}{\mathrm{k}}_{2}\mathrm{t}}$$
(6)
$$\frac{t}{q(t)}= \frac{t}{{q}_{e}}+\frac{1}{{k}_{2}{{q}_{e}}^{2}}$$
(7)

Scaling swelling model

The scaling swelling equation for the modeling of the swelling experimental result was initially derived by Lalji et al. in 2021. This model was formulated by using four basic parameters associated with LDSM and shale. These parameters were time of contact between shale sample and the drilling fluid (t), clay content in percentage obtained from XRD reports (C), swelling experimental results gathered from LDSM (S) and temperature (T) of the cell that has been recorded by LDSM. All these four variables along with two fine-tune adjustable parameters (n and \({a}_{1})\) and a universal constant (\({a}_{2})\) were grouped into two equations as shown by Eq. (8) and Eq. (9). It was observed during the study that the optimum values for n and \({a}_{1}\) lie in the range of 0.1–0.5, while for \({a}_{2}\) it was fixed at − 2.

$$X= \frac{t}{{T}^{n}*{C}^{{a}_{1}}}$$
(8)
$$Y= \frac{\mathrm{S}}{{t}^{{a}_{2}}}$$
(9)
$$Y= {A}_{4}+{A}_{3}X+{A}_{2}{X}^{2}+{A}_{1}{X}^{3}$$
(10)

Curves between temperature of the cell vs. time and swelling percentages vs. time are obtained during the course of the experimentation in LDSM. Both of these curves collapse into a single curve that is represented by the two variables X and Y as shown by Eqs. (8) and (9). A third-degree polynomial equation as shown in Eq. (10) best describes the relationship between these two variables. Here,\({ A}_{1}\),\({ A}_{2}\), \({A}_{3} \mathrm{and} {A}_{4}\) are coefficients of the scaling equation that are obtained by tuning the adjustable parameters that cause the line to be best fit. The adjustable parameters both n and \({a}_{1}\) are obtained from the MATLAB optimization tool. During this study, the optimum values of these two fine-tune parameters are 0.25.

Methodology

Data preparation for modeling

The experimental swelling results are collected from two research studies conducted by Khan, M.A. et al. in 2021and Lalji et al. in 2021 (Lalji et al. 2021). The swelling experimental result comprises three different shale formations, namely Talhar, Ranikot and Murree. Table 1 reports the characteristics of all the formations used in the modeling. The maximum swelling percentages were obtained from LDSM.

Table 1 Characteristics of shale formations used in the study
Full size table

Swelling for both Talhar and Ranikot formations was observed in salt polymer mud system, while for Murree formation graphene oxide amine water-based mud system was used for analyses. It was observed that the swelling characteristic of Talhar formation was on the low side because of the presence of a small quantity of clay minerals as also shown in Table 1. On the other hand, both Ranikot and Murree formations comprise approximately the same weight percentages of the clay content, but still the swelling percentages of Ranikot formation are comparatively higher than the Murree formation. This is because of the presence of higher concentration of Smectite in Ranikot formation in contrast with Murree formation. Figure 1 illustrates the flowchart for the comparative study followed during this research work.

Fig. 1
figure 1

Flowchart showing the comparative analyses process conducted between kinetics adsorption and scaling swelling model for different shale formations

Full size image

Models performance evaluation

The performance analysis of all the kinetic adsorption models and scaling swelling models was performed using statistical error analysis sources, namely MAE and absolute percent relative error (%APRE). Equations (11) and (12) show the equations used for calculation of these two factors.

$$\mathrm{MAE}= \frac{1}{\mathrm{N}}\sum_{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{y}}_{\mathrm{exp}}- {\mathrm{y}}_{\mathrm{est}}\right|$$
(11)
$$\mathrm{\% APRE}= \frac{1}{\mathrm{N}}\mathrm{abs}\left(\frac{{\mathrm{y}}_{\mathrm{exp}}-{\mathrm{y}}_{\mathrm{est}}}{{\mathrm{y}}_{\mathrm{exp}}}\right)*100$$
(12)

where \({y}_{\mathrm{exp}}\), \({y}_{\mathrm{est}}\) and N represent the experimental swelling values, model-estimated swelling values and the number of data points, respectively. For further in-depth analysis, graphical error analysis that comprises absolute error bar chart, relative error plot and cross-plot between experimental and predicted swelling percentages was formulated.

Moreover, ANOVA with the use of MINITAB was also conducted, where each predicted experimental swelling result was compared with the actual linear dynamic experimental swelling result. The method is based on comparing the \({F}_{\mathrm{calculated}}\) value with \({F}_{\mathrm{critical}}\) value. If \({F}_{\mathrm{calculated}}> {F}_{\mathrm{critical}},\) then null hypothesis has to be rejected, thus indicating a significant difference between the two datasets. Another comparison was made based on p values. If the p values are less than α = 0.05, then again a significant difference lies between the two groups. This analysis was performed on all the three samples of shale formations in order to observe the similarities in trend between them. Comparison of mean and variances of all the models with the experimental result was also made in this study.

Results and discussion

Figure 2a–d shows the absolute error plots for different kinetic adsorption models that comprise Peleg’s model, first-order exponential association equation, pseudo-second-order kinetic and scaling swelling model, respectively. Looking at Fig. 2, it can be observed that the scaling swelling model is found to be more accurate in estimating the shale swelling percentages obtained from linear dynamics swell meter than any of the kinetics adsorption models. The maximum magnitude of the absolute error obtained from the scaling swelling model was 0.5%, thus indicating a deviation of 0.5% from the experimental dataset. On the other hand, when comparing the kinetic adsorption models with each other, it is observed that pseudo-second-order kinetic model was found to be more precise than either Peleg’s model or first-order exponential association equation in estimating the swelling percentages of all the three shale samples. The maximum deviation in pseudo-second-order kinetic model is 1.5%, which is almost four times smaller in magnitude than Peleg’s model and twice smaller in size than the first-order exponential equation.

Fig. 2
figure 2

Absolute error plots. a Peleg’s model, b first-order exponential association equation, c pseudo-second-order kinetic, d scaling swelling model

Full size image

Figure 3 displays the relative error plots for all the three shale samples obtained from different regions of Pakistan. Referring to Fig. 3, comparing the performances of all the kinetic adsorption models along with the scaling swelling model in estimating the swelling percentages, it was observed that in all the three different shale formations the scaling swelling model performance was the best in estimating the swelling values. The lines for scaling swelling model fall close to x-axis, thus indicating lower percentages of the errors at all different time zones. Conversely, when comparing the kinetic adsorption models, it was evident that Peleg’s model performance was relatively weaker in terms of predicting the swelling percentages for all the three samples. Therefore, it is not recommended to use Peleg’s model while predicting the swelling percentages of a shale sample as it is not better qualified in predicting the swelling values. The values for characteristics constants \({k}_{1}\) and \({k}_{2}\) in Peleg’s model for all the three samples are shown in Table 2. It can be witnessed that for higher swelling samples as reported in Table 1, the characteristic constant values are on the lower side, thus indicating an inversely proportional relationship with the clay contents. This exhibits an increase in absorption capacity of the shale sample with an increase in clay content. This finding is in agreement with the finding of Maskan (Maskan 2002) and Solomon (Solomon 2007), where they reported high absorption capacity of water in correspondence with lower values of \({k}_{1}\) and \({k}_{2}\).

Fig. 3
figure 3

Relative error plots. a Talhar formation, b Ranikot formation, c Murree formation

Full size image
Table 2 Estimated parameters of the Peleg’s model for different shale samples
Full size table

Furthermore, when comparing the first-order exponential association equation and pseudo-second-order kinetics in predicting the shale swelling behavior it was perceived that pseudo-second-order kinetics was found better in correlating the experimental dataset. Table 3 represents the regression values for swelling kinetics constants \({k}_{1}\) and \({k}_{2}\) used in both the models.

Table 3 Estimated regression parameters of the first-order exponential association equation and pseudo-second-order kinetics
Full size table

In the majority of the literature found on adsorption kinetics, \({k}_{2}\) gains significant popularity and superiority in providing the best relationship of the experimental dataset (Simonin 2016; Ho 2006). The best correlation is established when \({k}_{2}>{k}_{1}\) (Simonin 2016). This inequality is proven during this research work, as the values of \({k}_{1}\) and \({k}_{2}\) obtained during regression modeling show the validation of this relationship. The efficacy of this correlation is further shown in Fig. 3 relative error plots, where in all the shale samples the pseudo-second-order kinetics in all the kinetic adsorption models prove to be more efficient in estimating the swelling percentages. On the other hand, the scaling swelling model was proved to be more effective than any of the adsorption kinetic models. This can be observed by the accumulation of all the datasets closer to the horizontal line in Fig. 3. The tuning parameters in the scaling swelling model ensure an excellent agreement between the experimental and predicted datasets.

Figure 4 shows the cross-plots between the experimental datasets and model-predicted values, which are obtained using different kinetics adsorption models and scaling swelling equation. Referring to the figure, it is evident that scaling swelling model performance was best as all the data points fall on the perfect model line that is equal to \(y=x.\) Moreover, pseudo-second-order kinetics equation ranked second in predicting the swelling percentages of different shale formations. As far as Peleg’s model is considered, the error band for this model lies outside the ± 10%, thus indicating the poor performance in estimating the kinetics of the shale. The transient period for this model continues to the end of the experiment without reaching the equilibrium state. Hence, the swelling percentages are always under-predicted as it can be witnessed from all the three plots below, where Peleg’s model swelling dataset always lies under the perfect model line.

Fig. 4
figure 4

Cross-plots for kinetics adsorption models and scaling swelling equation. a Talhar, b Ranikot, c Murree formations

Full size image

Additionally, it was further detected that for the first-order exponential association kinetics equation if the clay content is on the higher side as in Murree and Ranikot formations, then this model over-predicts the swelling response, while for Talhar formation where the clay content is only 10 wt% the swelling is under-predicted.

A plot of swelling percentages vs. experimental time (h) is shown in Fig. 5. It can be observed that the scaling swelling model was proved to be best in estimating the swelling percentages. While when comparing between the two kinetic models, pseudo-second-order kinetic was effective in predicting a closer response for swelling in all the three samples. This was also validated further when both the kinetic models were plotted in the form of linear function using Eqs. (4) and (7). The linear relationship plots for both the kinetics model are shown in Fig. 6. It was observed that \({k}_{2}\) gives the best coefficient of correlation for all the shale samples as the values obtained for \({R}^{2}\) as reported in Table 4 are higher and closer to 1. When defining \({k}_{1}\) in terms of linear relationship, it was observed from Fig. 6 that some of the datasets show deviation from linear behavior when swelling reached its equilibrium state. The agreement with \({k}_{2}\) in this study typically occurs because the period for transient state in all the three samples is relatively smaller; this indicates that a significant number of swelling percentages are closer to the equilibrium state. Hence, when plotting Eq. (7), the points that are closer to equilibrium or are at equilibrium state automatically get well aligned because the condition \(\frac{t}{q(t)} \simeq \frac{t}{{q}_{e}}\) is satisfied (Simonin 2016). For this particular reason, correlation coefficient is also closer and equal to 1, while on the other hand, for \({k}_{1}\) when the S(t) approaches closer to \({S}_{e}\) the value of (\({S}_{e}-S\left(t\right))\) gets smaller and smaller and that corresponds to an increase in value of \({[[\mathrm{ln}(S}_{e}-S\left(t\right))]\). This phenomenon reduces the accuracy of \({k}_{1}\) parameter (Simonin 2016). This clearly indicates that all the shale formation follows the pseudo-second-order kinetics model during their adsorption process. Hence, this suggested that shale swelling is a chemisorption process in which swelling depends on adsorption capacity rather than concentration of the shale.

Fig. 5
figure 5

Simulated swelling percentages of kinetics adsorption models and scaling swelling model for a Talhar, b Ranikot, c Murree formations

Full size image
Fig. 6
figure 6

Two-parameter plots for with k1 (a, c, e) and k2 (b, d, f) swelling constants for all the shale samples

Full size image
Table 4 Two parameters k1 and k2 results with R2
Full size table

On the contrary, Peleg’s model performance was worse in predicting the swelling behavior for shale samples. It is evident that for this model that the transient state continues till the end of the experimentation. This clearly indicates higher and continuous adsorption of water molecules within the shale sample. For this model, no equilibrium state was observed during the entire process of the experimentation.

Table 5 shows the mean absolute error (MAE %) and absolute percent relative error (APRE %) of different kinetic adsorption models and scaling swelling model for all three shale samples. It can be seen from the table that the performance of the scaling swelling model is far better than any of the kinetic adsorption model in terms of predicting the swelling percentages. The lower the values of MAE, the more accurate will be the performance of the models in validating the experimental results. When comparing the first-order exponential association equation with pseudo-second-order kinetics, it was observed that in all the formations, pseudo kinetic behavior in shale swelling is dominant because of lower MAE than the first-order exponential association equation. However, with the increase in clay content the performance of both of these models deteriorates significantly as indicated with higher MAE values. Moreover, Peleg’s model in neither of the shale samples was effective in predicting the swelling behavior. This model always underestimates the swelling behavior throughout the entire experimental process. This result was also confirmed by another statistical tool denoted as APRE %.

Table 5 Mean absolute error (MAE) and absolute percent relative error (APRE %) for kinetic adsorption models and scaling swelling model for all three shale samples
Full size table

ANOVA analysis

To further prove the difference between the predicted experimental results and actual experimental results, ANOVA was performed on all three shale formation results. Table 6 reports the results of ANOVA obtained from MINITAB for Talhar formation. A total of 25 dataset points were used in this study. It is evident from the table that only Peleg’s model for adsorption was not in good agreement with the experimental results. The \({F}_{\mathrm{calculated}}> {F}_{\mathrm{critical}}\) relationship was true in this case only; hence, it indicates that both the groups have some significant differences between these results. Moreover, based on the p values again this conclusion was true for Peleg’s model because its p values < α(significance level = 0.05). Furthermore, when the mean and variances of these two groups were investigated, it was observed that there were some substantial differences that lie between the two groups. Apart from Peleg’s model, remaining all the models showed behavior closer to the experimental datasets as both the above-mentioned conditions were opposite to the one obtained from Peleg’s model. Hence, it can be concluded that the null hypothesis is failed to reject these models, thus indicating an equal mean of the dataset groups. Moreover, while analyzing the variation in mean between the groups in Talhar formation, it was observed that Peleg’s model and pseudo-second-order kinetic model both satisfy the condition \({\mathrm{Mean}}_{\mathrm{experimental }}>{\mathrm{Mean}}_{\mathrm{model}}\). This clearly indicates the under-prediction of the models’ swelling results and can also be confirmed from Fig. 5a. Alternatively, the first-order exponential association equation in Fig. 5a shows the over-prediction result and can be confirmed from the condition \({\mathrm{Mean}}_{\mathrm{experimental }}<{\mathrm{Mean}}_{\mathrm{model}}\). And finally, the scaling swelling model satisfies the condition \({\mathrm{Mean}}_{\mathrm{experimental }}{\simeq \mathrm{Mean}}_{\mathrm{model}}\) from Table 6. This clearly indicates the perfect match of the experimental swelling results with model swelling results and can be validated from Fig. 5.

Table 6 ANOVA between experimental swelling percentages and models swelling percentages for Talhar formation
Full size table

The result obtained from ANOVA for the remaining two shale formations as shown in Tables 7 and 8 showed similar trends. Here, again Peleg’s model was not in good agreement with the experimental swelling percentages. In contrast, the scaling swelling model in ANOVA showed an excellent agreement with the experimental work. The values for mean and variances are almost equivalent to the actual values obtained from experimentation for this model.

Table 7 ANOVA between experimental swelling percentages and models swelling percentages for Ranikot formation
Full size table
Table 8 ANOVA between experimental swelling percentages and models swelling percentages for Murree formation
Full size table

Variance analysis

Variance is defined as the spreading of data points or divergence from the mean position. Table 6 shows the comparison of the variances for all the models with experimental datasets. It is evident that \(\mathrm{the}{\mathrm{ Variance }}_{\mathrm{Peleg}}\gg \boldsymbol{ }{\mathrm{Variance }}_{\mathrm{Experimental}}\), thus indicating a very large dispersion of the dataset points from the mean position. High scattering of the data points was also observed in the first-order exponential association kinetic equation, with \({\mathrm{Variance }}_{\mathrm{First order}}> {\mathrm{Variance }}_{\mathrm{Experimental}}\). Similar behavior was also perceived in pseudo-second-order kinetics model; however, the scattering was minimal when comparing with other two already discussed models. On the other hand, when the scaling swelling model was investigated it was witnessed that the \({\mathrm{Variance }}_{\mathrm{Scaling Swelling}}\simeq {\mathrm{Variance }}_{\mathrm{Experimental}}\). This indicates a relatively higher performance when compared with other three kinetic models. Analogous trends were also observed in both Ranikot and Murree formations.

Conclusion

The comparative study was based on comparing the different kinetic adsorption models, namely Peleg’s model, first-order exponential association equation and pseudo-second-order kinetics with scaling swelling model in predicting the shale swelling behavior obtained from linear dynamic swell meter. During the analysis, it was observed that Peleg’s adsorption model was the weakest in predicting the swelling behavior. The transient state for this model never reaches the equilibrium state during the entire course of experimentation. Similarly, when the comparison was made between the two major kinetic models, it was witnessed that in all the three samples pseudo-second-order kinetic behavior was dominant. In all the cases, the inequality \({k}_{2}>{k}_{1 }\) was observed. However, it was also observed from the analyses that as the clay content increases such as that in the Ranikot formation where percentage of clay is equal to 30%, the performance of both the kinetic models drastically suffers. This was indicated by the statistical error analyses based on MAE and APRE %. Both these error sources increase significantly in Ranikot formation. On the contrary, when the scaling swelling model was implemented in predicting the swelling behavior of shale the results were quite astonishing. It was perceived that the accuracy of this model was far better than any of the kinetic models. As this model is based on fine-tuning parameters and some of the most important governing factors are responsible for shale swelling, the prediction of the swelling behavior is extremely close to the experimental results. This was indicated with the help of lower values of MAE and APRE %. Hence, it can be concluded that the scaling swelling model can easily be used in predicting the swelling behavior in shale because it offers less complexities as compared to kinetic adsorption modeling based on regression. This conclusion was further evaluated using the ANOVA. This analysis showed a significant difference between the Peleg’s model and the experimental dataset, while remaining all the models demonstrate results closer to LDSM experimental swelling results.