Insight into Debye Hückel length (κ⁻¹): smart gravimetric and swelling techniques reveals discrepancy of diffuse double layer theory at high ionic concentrations

Abstract

Smart gravimetric and swelling techniques were utilized in this work to examine the validity of the Debye Hückel length (κ⁻¹) equation when shale interacts with highly concentrated salt solutions. The swelling and shrinkage behavior of two different shales, when exposed to monovalent and divalent ionic solutions (NaCl, KCl and CaCl₂) at concentrations ranging from 2 to 22%w/w was observed and measured. Shale swelling and shrinkage results show that Debye Hückel length (κ⁻¹) equation seems to work adequately at low ionic concentrations where osmotic water flow out of shale plays a major role in decreasing the diffuse double layer thickness by withdrawing water out and thereby shrinking κ⁻¹. At high ionic concentration levels, the flow of associated water into the diffuse double layer negates the withdrawal of osmotic water out of the diffuse double layer which could maintain κ⁻¹ or possibly increase it. Data on measured ionic uptake into shale suggests that excessive ionic diffusion into shale, especially at high concentrations, leads to higher electrical repulsion between alike ions in the diffuse layer which could lead to the expansion of the diffuse double layer thickness. Furthermore, swelling and shrinkage data analysis for shale suggests the existence of a ‘critical concentration’ below which the Debye Hückel length equation works. Above the critical concentration, the validity of the Debye Hückel length equation might be in question. The critical concentration is different for all ions and depends on ionic valence, hydrated ion diameter, and clay type.

Introduction & literature review

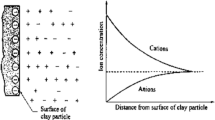
Shale is known for its low permeability and negatively charged surface. Its negative charge is produced through a process known as isomorphic substitution where a lower valent ion such as Al³⁺ replaces a higher valent ion such as Si⁴⁺ in the tetrahedron, which creates an excess of negative charges on clay surfaces. Clay minerals display isomorphic substitutions that produce both positive and negative charges on their surfaces. The presence of negative charges on clay surfaces enables shale to adsorb water, which could cause shale hydration and subsequent swelling (van Oort 2003). Negative charges on clay surfaces facilitate the transport of cations and prevent the transport of anions, which could impact swelling properties and mechanical integrity of shale (Lomba et al. 2000). The transport and distribution of cations near negatively charged clay surfaces create what is described by the DLVO theory as a diffuse double layer. The diffuse double layer includes both the Stern layer and diffuse layer as depicted in Fig. 1. The thickness of the diffuse double layer is approximated by the Debye Hückel length. In an electrolyte or a colloidal suspension, the Debye Hückel length for a monovalent electrolyte is frequently represented with symbol κ⁻¹ as follows:

$$\kappa^{ - 1} = \sqrt {\frac{{\varepsilon_{{\text{r}}} \varepsilon_{0} k_{{\text{B}}} T}}{{2N_{{\text{A}}} e^{2} I}}}$$

(1)

where; ε_r: dielectric constant of water = (78.5 at 25C = 298 K), ε₀: permittivity of free space = 8.85E-12 C²/ (J.m), k_B: Boltzmann constant = 1.38E-23 (J/K), T: the absolute temperature in Kelvins (K), N_A: Avogadro number = 6.02E23 (1/mols), e: elementary charge = 1.6E-19 C, I: ionic strength of the electrolyte in molar units (M or mol/L), Z: valance of ion (Na⁺  = 1; Cl⁻ = 1; Ca⁺² = 2; Mg⁺² = 2), $\kappa^{ - 1}$: Debye Hückel length (m).

Fig. 1

Diffuse double layer (Suopajärvi 2015)

The ionic strength of the electrolyte is given by:

$$I = \frac{1}{2}\mathop \sum \limits_{i} z_{i}^{2} c_{i}$$

(2)

where z_i is the valence of the ith ion, c_i is the concentration of the ith ion in mol/L and i covers all types of ions in the electrolyte solution. According to Eq. (2), multivalent ion solutions have larger ionic strength (I) than monovalent ion solutions. Taking into account Eq. (2) and substituting all constants in Eq. (1) yields:

$$\kappa^{ - 1} = \frac{{0.304 \left( {{\text{nm}}} \right)}}{\sqrt I };\;{\text{for}}\;{\text{monovalent}}\;{\text{ ionic}}\;{\text{ solutions }}\left( {{\text{NaCl}},\;{\text{ KCl}}} \right)$$

(3)

$$\kappa^{ - 1} = \frac{{0.192553 \left( {{\text{nm}}} \right)}}{\sqrt I };\;{\text{for}}\;{\text{ divalent}}\;{\text{ ionic}}\;{\text{ solutions }}\left( {{\text{CaCl}}_{2} ,\;{\text{ MgCl}}_{2} } \right)$$

(4)

It is important to mention that Eq. (4) serves as an approximate average of κ⁻¹ for a wide range of divalent ionic solutions. Different concentrations of divalent ionic solutions may have different forms of Eq. (4); however, using an approximate average is acceptable qualitatively.

The thickness of the diffuse double layer determines the stability of colloidal suspensions in aqueous solutions where small values of κ⁻¹ promote stability and high values of κ⁻¹ lead to dispersion and instability (Smith et al. 2016; Bohinc et al. 2001; McBride 1997). For small values of κ⁻¹, it is believed that the attractive van der Waals forces overcome repulsive electrostatic forces within the diffuse double layer and bring the charged clay surfaces closer and prevent dispersion of clay. On the other hand, repulsive electrostatic forces within the diffuse double layer are believed to dominate the weaker van der Waals forces at higher values of κ⁻¹ causing clay dispersion. Darjani et al. (2021a) and Darjani et al. (2021b) investigated the effect of electrostatic repulsion forces between adsorbed particles at high surface concentrations and reported the occurrence of a sharp disorder-order transition in the system at high surface concentration when increasing the chemical potential.

As seen in Eq. (1), κ⁻¹ is inversely proportional to the square root of the ionic concentration. AL-Bazali (2021) presented experimental evidence confirming the notion that concentrated potassium chloride solutions suppressed shale swelling at higher concentrations of potassium ions. This has encouraged the idea of using concentrated salt solutions for clay and shale stability, especially when dealing with highly reactive (water-sensitive) shales.

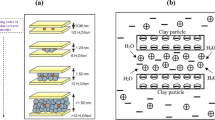
When two solutions of different chemical potentials are separated by a semi-permeable membrane, water flows osmotically in the direction of the lower chemical potential solution as shown in Fig. 2. The chemical potential of aqueous solutions can be estimated by their water activities (Chenevert 1970). The magnitude of developed osmotic pressure (π) is given by:

$$\pi = \left( {RT/V_{w} } \right) \, \ln \, (a_{w1} /a_{w2} )$$

(5)

where R is the gas constant, T is the absolute temperature, V_w is the partial molar volume of water, and a_w1 and a_w2 are the water activities of solutions. Water activities of aqueous solutions are manipulated by the addition of solutes (ions) which lower their chemical potentials and water activities. While the addition of solutes to a solution lowers its water activity, it increases its ionic concentration and encourages ionic diffusion and diffusion osmosis when exposed to other solutions of lower ionic concentrations (T. AL-Bazali 2013b; Ghassemi et al. 2001; Simpson and Dearing 2000). Ionic diffusion is the transport of ions from a concentrated solution to a dilute one and is governed by Fick’s law as follows:

$$J \, = \, - \, D_{i} * \, \left( {C_{i1} {-} \, C_{i2} } \right) \, /DL$$

(6)

where J is mass flux of ith ion; D_i the diffusion coefficient of the ith ion; C_i1 is the concentration of ith ion in shale’s pore fluid; C_i2 is the concentration of ith ion in salt solution and ΔL is shale’s length. Diffusion osmosis is the transfer of associated water ‘’water cloud’’ along with their respective ions in the direction of lower ionic concentration. Table 1 shows the hydrated ion radius and un-hydrated ion radius for several ions. Therefore, when two aqueous solutions of different concentrations (water activities) interact across a semi-permeable membrane, water and ions exchange according to the following:

Fig. 2

Direction of osmotic water in the direction of lower chemical potential solution

Table 1 Hydrated ion radius and un-hydrated ion radius for several ions

• Osmotic water moves towards the concentrated solution (lower water activity).

• Associated water moves towards the dilute solution (higher water activity).

• Ions diffuse towards the dilute solution (higher water activity)

The DLVO theory argues that the amount of cations and water in the diffuse double layer determines its thickness (κ⁻¹). A higher amount of cations is thought to decrease κ⁻¹ promoting attraction and stability, while an excessive amount of water is believed to increase κ⁻¹ leading to repulsion and instability (Stillinger and Kirkwood 1960). Ideally, decreasing κ⁻¹ can be achieved by osmotically drawing water out of and or encouraging cationic diffusion into the diffuse double layer, and this could be accomplished by lowering the water activity (increasing cationic concentration) of the solution in contact with clay particles of shale. This argument holds true if Eq. (1) works at all ionic concentrations. Using a combination of linear swelling tests and newly developed gravimetric techniques, this work tests the validity of Eq. (1) when shale interacts with aqueous solutions at a wide range of solute concentrations. More precisely, the impact of ionic size, valence and concentration on the diffuse double layer thickness κ⁻¹ is investigated. Moreover, the operational zone (range) of both osmotic water and associated water within the diffuse double layer is addressed. Guidelines for better shale instability mitigation are also outlined.

Experimental methodology

Shale cores utilized in this work were donated by an oil company operating in Kuwait. Proper persuasions were taken to minimize the interaction of shale cores with air during coring, handling, storing, and transporting. The mineralogical compositions of shales (A) and (B) are shown in Table 2, while their physical, chemical and petrophysical properties are shown in Table 3. Methods for obtaining mineralogical composition, water content, water activity, porosity, and permeability for shales (A) and (B) are explained next. Three salts were used in this study; NaCl (purity 99.5%), KCl (purity 99.8%), and CaCl₂ (purity 99.9%). These salts were provided by a local chemical supplier in Kuwait.

Table 2 Mineral make-up (structure) of shales A & B

Table 3 Native physical, chemical and petrophysical properties of shales A & B

Mineralogical composition test

X-ray Diffraction was determined by an independent commercial testing facility located in the USA. The composition and crystalline structure of both shales was achieved through the identification of angles at which the x-Ray beam (λ ranges from 0.01 to 100Ǻ) is diffracted as discussed in Breeden and Shipman (2004).

Water content test

A dry by heat method was employed to obtain the water content (moisture content) of the shale. A fully saturated cylindrical shale sample (radius = 1’’, length = 3.5’’) was initially weighted (W_s) and then placed in an oven at 200F. After 24 h, the shale sample was taken out of the oven and weighted (W_d). It is argued that 24 h is sufficient to remove all free water inside the shale pores (Zhang et al. 2006). The water content (W_c) is determined as follows:

$$W_{{\text{c}}} \;\% = \left( {\frac{{W_{{\text{s}}} - W_{{\text{d}}} }}{{W_{{\text{s}}} }}} \right)*100$$

(7)

where W_s is the weight of the saturated shale sample and W_d is the weight of the shale sample after heat drying for 24 h.

Water activity test

The water activity of the shale was determined using an adsorption isotherm methodology where fully saturated shale samples were placed in several desiccators of different water activities. Saturated salt solutions (Table 4) were utilized to obtain and maintain desiccators water activities at desired levels. A detailed description of this test can be found in AL-Bazali et al. 2008.

Table 4 Saturated salt solutions used to maintain desiccators water activities at desired levels

Porosity test

The standard API drying by heat methodology was applied to measure the porosity of shale. A fully saturated cylindrical shale sample (radius = 1’’, Length = 3.5’’) was initially weighted (W_s). The shale sample was then placed in an oven at 200F for 24 h and then weighted again (W_d). Since the shale sample is fully saturated, it is reasonable to assume that the volume of water lost during the drying process is equivalent to the shale’s pore volume. The water volume (V_w) lost during drying equals to the weight reduction experienced by shale when heated. The volume of water lost during the shale drying process (V_w) is approximated as:

$$V_{{\text{w}}} = \frac{{W_{{\text{s}}} - W_{{\text{d}}} }}{{\rho_{{\text{w}}} }}$$

(8)

where ρ_w represents the water density.

Since the shale sample is assumed to be fully saturated, it is fair to state that the shale’s pore volume (V_p) equals to the volume of water lost during the shale drying process (V_w). Therefore, shale’s porosity ($\varphi$) can be calculated as follows:

$$\varphi = \frac{{V_{{\text{p}}} }}{{V_{{\text{t}}} }}$$

(9)

where V_t represents the shale’s total (bulk) volume.

Permeability test

Standard pressure transmission methodology, similar to that used by Oleas et al. (2010), was employed to obtain permeability of shales (A) and (B).

Swelling test

Shale samples were placed in a small plastic bag and positioned between the movable anvil and the stationary anvil of a standard linear swelling device. A 50 ml of salt solution is poured into the plastic bag hosting the shale sample and air is squeezed out and the bag is firmly sealed. The amount of swelling or shrinkage of shale as it interacts with NaCl, KCl and CaCl₂ solutions of 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and 22%w/w were attained by dividing the increase or decrease in sample length, displacement reading, by the original sample length. A standard stop watch was used to monitor the swelling time of shale as it interacts with salt solutions. The swelling test is terminated after 24 h. A graph of swelling or shrinkage (%) of shale versus time (minutes) is generated as a function of salt type (NaCl, KCl and CaCl₂) and concentration. This technique allows us to measure shale swelling and at the same time quantify water and ions uptake for the same sample where swelling occurs. This method makes shale swelling analysis more relevant, especially since shale’s swelling is believed to be highly related to water and ions uptake (AL-Bazali 2013a).

Water and ions uptake test

Water and ions uptake into shale when interacting with NaCl, KCl and CaCl₂ solutions of 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and 22%w/w is made possible by the use of a gravimetric technique where weight changes of well-preserved shale samples are measured in different conditions. The following equations calculate the amount of water and ions gained or lost as a result of shale interaction with salt solutions.

$$W_{w} \% \, = \left( {\frac{{W_{3} - W_{4} - W_{1} + W_{2} }}{{W_{1} }}} \right)*100\%$$

(10)

$$W_{i} \% = \left( {\frac{{W_{4} - W_{2} }}{{W_{1} }}} \right)*100\%$$

(11)

W₁: Weight of preserved sample in air, W₂: Weight of preserved sample after drying. W₃: Altered weight of sample after immersion in salt solutions, W₄: Dry weight of altered sample, W_w%: Weight of water transferred into (gain) or out of (loss) shale, W_i%: Weight of ions transferred into (gain) or out of (loss) shale.

It is vital to indicate that W_w% obtained by Eq. (10) signifies net water % uptake into or out of shale. This net water combines osmotic water due to the presence of chemical potential and associated water transported along with diffusing ions owing to ionic concentrations imbalances between shale and salt solutions.

Osmotic and associated water test

To separately quantify the amount of osmotic water and the amount of associated water, fresh samples of native preserved shale were weighed and then placed in desiccators containing NaCl, KCl and CaCl₂ solutions of 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and 22%w/w. The corresponding water activities of these solutions at these selected concentrations are shown in Fig. 3. The concentration of each salt solution is constantly monitored and maintained at the desired concentration. The shale sample’s weight is observed daily until no further change is reported. The final sample’s weight is recorded. The difference between the shale’s initial weight and the final weight is taken as osmotic water. Subtracting the osmotic water, respectively, from the net water uptake as a result of shale interaction with NaCl, KCl and CaCl₂ solutions at each corresponding concentration yields the amount of associated water transported by diffusion osmosis. Osmotic water and associated water are given by:

$$W_{{{\text{osmotic}}}} = W_{1} - W_{2}$$

(12)

$$\% W_{{{\text{osmotic}}}} = \frac{{W_{{{\text{osmotic}}}} }}{{W_{1} }}$$

(13)

$$\% W_{{{\text{associated}}}} = \% W_{w} - \% W_{{{\text{osmotic}}}}$$

(14)

where; W₁: Initial weight of preserved shale sample in air. W₂:Final weight of shale sample after placed in the desiccators containing NaCl, KCl and CaCl₂ solutions. %W_osmotic: Water uptake into shale due to chemical osmosis. %W_associated: Water uptake into shale due to diffusion osmosis. % W_w: Net water uptake into shale and is given by Eq. (10).

Fig. 3

NaCl, KCl & CaCl₂ water activities as a function of concentration (%w/w)

Results & analysis

Debye Hückel Length (κ⁻¹ ) theoretical calculation

Using % weight concentration unit instead of molar concentration unit for salt solutions makes it easier to compare κ⁻¹ predictions made by Eqs. (3 and 4) with experimental swelling test results as discussed in the “Linear swelling tests on shale” Section. Conversion of molar concentration to % weight concentration for NaCl, KCl and CaCl₂ is shown in Fig. 4. Figure 5 shows Debye Hückel length (κ⁻¹) as a function of ion’s type, valance and concentration (% w/w) as predicted by Eqs. (3) and (4). This figure shows that κ⁻¹ decreases as ionic valence and hydrated diameter increase. At similar ionic concentrations, CaCl₂ with a valence of 2 produced a value of κ⁻¹ that is less than that produced by NaCl and KCl which have an ionic valence of 1. Also, at the same ionic concentrations, NaCl produced lower values of κ⁻¹ than that produced by KCl despite their similar ionic valence (z_i = 1). This is due to the fact that the hydrated diameter of Na⁺ is greater than that of K⁺ as shown in Table 1. More importantly, Fig. 5 shows that for all ions, κ⁻¹ decreases as ionic strength (concentration) increases. The Debye Hückel length equation assumes that κ⁻¹ and the ionic strength inverse relationship holds true at all concentrations for all ions. I believe that while this may hold true for pure colloidal clays, it may not be consistent for clayey shales due to their complex structures and compositions. Linear swelling tests on clayey shales were utilized to investigate this matter.

Fig. 4

Molarity of NaCl, KCl and CaCl₂ as a function of ionic concentration (%w/w)

Fig. 5

Debye Huckel length (κ⁻¹) as a function of ion’s type, valance and concentration (% w/w)

Linear swelling tests on shale

Figure 6 shows Shale (A) swelling and shrinkage profile when exposed to NaCl, KCl and CaCl₂ solutions at different concentrations (%w/w). The following key points are deduced from Fig. 6:

• For all salts, shale shrank as salt concentration increased up to a certain concentration, after which it swelled. The shrinkage and swelling of the shale can be interpreted microscopically as a decrease and increase in the diffuse double layer thickness (κ⁻¹) respectively. The change from shrinkage to swelling behavior is different for all salts. Shale shrinkage occurred up to 12%w/w CaCl₂ concentration, after which swelling took over. Shale shrank up to 14%w/w NaCl concentration while it shrank up to 16%w/w KCl concentration. This does not agree with predictions made by Eqs. (3 and 4) where it shows that κ⁻¹ decreases at all concentrations for all ionic types.

• Up to 12%w/w concentration, CaCl₂ showed the highest shrinkage followed by NaCl and KCl, respectively. This agrees with predictions made by Eqs. (3 and 4) where it clearly shows, as seen in Fig. 6, that κ⁻¹ values produced by CaCl₂ up to 12%w/w concentration are the lowest of all salts followed by NaCl and KCl, respectively. This could be attributed to the higher ionic valence and hydrated diameter of CaCl₂ when compared to the other monovalent ions (NaCl and KCl). Despite their equal ionic valences (z_i = 1), NaCl produced lower values of κ⁻¹ than KCl up to 14%w/w concentration and this could be due to its bigger hydrated diameter.

• After a critical concentration (specific to each salt as discussed above) is reached, swelling occurs where CaCl₂ showed the highest swelling followed by KCl and NaCl, respectively as shown in Fig. 6. This does not agree with predictions made by Eqs. (3 and 4) where κ⁻¹ values are expected to decrease for all salts as concentration increases. Generally, the different swelling magnitudes for all salts could be attributed to their valences and hydrated diameters.

• At 20 and 2 2%w/w concentrations, swelling of KCl is higher than that of NaCl despite its lower hydrated diameter. Such observation does not coincide with predictions made by Eqs. (3 and 4).

Fig. 6

Shale (A) swelling and shrinkage profile when exposed to NaCl, KCl and CaCl₂ solutions

As seen from the above discussion, shrinkage and swelling behavior of shale sheds more light on the validity of Debye Hückel length equation. Swelling and shrinkage data suggests that Debye Hückel length equation may work very well at low concentrations and break down at higher concentrations. The critical concentration, below which the Debye Hückel equation works, is different for all ions and may depend on many factors such as ionic valence, hydrated diameter and clay type.

Figure 7 shows shale (B) swelling and shrinkage profile when exposed to NaCl, KCl and CaCl₂ solutions. It is readily seen that the magnitude of shrinkage of shale (B) is less than that of shale (A) for all salts. This is attributed to the fact that shale (A) has a higher water activity than shale (B) which creates a larger chemical potential imbalance when interacting with salt solutions. It is shown by many that water flows out of shale in the direction of lower chemical potential (water activity) regions (Manohar 1999; Fam and Dusseault 1998; Tao et al 2010). Similar to shale (A) observations, there exists a critical concentration above which shale swells for all ionic solutions. In the case of shale (B), the observed critical concentrations of CaCl₂, NaCl and KCl are 14, 16 and 18 %w/w, respectively. As seen, measured critical concentration values are higher for shale (B) than shale (A) when interacted with the same salt solutions. This could be attributed to the mineralogical composition and properties of shale as shown in Tables 2 and 3.

Fig. 7

Shale (B) swelling and shrinkage profile when exposed to NaCl, KCl and CaCl₂ solutions

Water and ions uptake quantification

Figures 8 and 9 show water and ions uptake into shale (A) and shale (B), respectively when interacted with NaCl, KCl and CaCl₂ solutions at different concentrations. It can be seen from these figures that ions flowed into both shales owing to the imposed ionic concentration gradient while water flowed out of both shales in response to the imposed chemical potential imbalance. It is also observed from Figs. 8 and 9 that water flows out of both shales seems to reverse its direction at a certain salt’s concentration where the amount of water flow out of shale decreases noticeably despite the ever-increasing chemical potential imbalance. Water flow reversal in shale (A) occurred at the same critical concentrations where shale (A) shrinkage was changed to swelling; 12%w/w CaCl₂, 14%w/w NaCl and 16%w/w KCl. As for shale (B), water flow reversal occurred at 12, 14 and 16%w/w for CaCl₂, NaCl and KCl, respectively. These concentration values at less than the critical values at which shale (B) shrinkage was reversed to swelling. To fully examine water flow into or out of shale, a special gravimetric test is employed to separate the quantity of water uptake by chemical osmosis from that by diffusion osmosis. Such insight could bring us closer to understanding the shrinkage and swelling of shale at critical ionic concentrations.

Fig. 8

Water and ions uptake into shale (A) when interacted with NaCl, KCl and CaCl₂ solutions

Fig. 9

Water and ions uptake into shale (B) when interacted with NaCl, KCl and CaCl₂ solutions

Osmotic water versus associated water

Figures 10 and 11 show osmotic water and associated water uptake into shales (A & B), respectively when interacted with NaCl, KCl and CaCl₂ solutions at different concentrations. As expected, the osmotic flow of water out of both shales increases as the chemical potential (water activity) imbalance increases in conformance with Eq. (5). It is argued that withdrawal of water out of shale decreases the spacing between clay platelets and results in shale shrinkage (Zhang et al. 2004; Hale and Mody 1992; Madsen and Müller-Vonmoos 1989; Jiang et al. 2014).

Fig. 10

Osmotic water and associated water uptake into shale (A) when interacted with NaCl, KCl and CaCl₂ solutions

Fig. 11

Osmotic water and associated water uptake into shale (B) when interacted with NaCl, KCl and CaCl₂ solutions

It is also observed from Figs. 10 and 11 that associated water flow into shale increased as the ionic concentration difference between shale and salt solutions increased. This type of water is chemically bound to diffuse ions and forms a water cloud that moves along with its parent ion (AL-Bazali 2011; Denis et al. 1991). The reversal of shale shrinkage to swelling is obviously attributed to the increased flow of associated water as salt concentration increases. In other words, associated water works against osmotic water in the diffuse double layer where osmotic water produces shale shrinkage and thus lowers the value of κ⁻¹ and associated water causes shale swelling, thereby increasing the value of κ⁻¹. The amount of associated water seems to be highly related to the ion’s size where CaCl₂ produced a higher amount of associated water than monovalent ions (NaCl and KCl).

Putting it all together

The Debye Hückel length (κ⁻¹) as expressed in Eq. (1) seems to work adequately at low ionic concentrations. At low concentration levels, the osmotic flow of water out of shale plays a major role in decreasing the diffuse double layer thickness by withdrawing water out and thereby shrinking κ⁻¹. At high concentration levels, the flow of associated water into the diffuse double layer compensates for the withdrawal of osmotic water out of the diffuse double layer which could maintain κ⁻¹ or possibly increase it. It is quite possible that increasing ionic diffusion into shale, especially at high concentrations, leads to higher electrostatic repulsion between alike ions, which could expand the diffuse double layer thickness. This is evident by the shrinkage to swelling reversal behavior in both shales (A&B) at high ionic concentrations as shown in Figs. 6 and 7 and is supported by the increased ions uptake into both shales as seen in Figs. 8 and 9.

Research importance & future work

Using smart gravimetric and swelling techniques, this work investigated, for the first time, the impact of a wide range of ionic concentration levels on the Debye Hückel length development as shale interacts with ionic solutions. It was shown that there exists a ‘critical concentration’ below which the Debye Hückel length equation works. Above the critical concentration, the validity of the Debye Hückel length equation might be in question. Also, data suggest that the critical concentration is different for all ions and depends on ionic valence, hydrated ion diameter, and clay type. Other studies have presented work investigating changes in Debye Hückel length when clay was exposed to ionic solutions and have not studied a wide range of concentrations as these studies have only investigated the impact of certain ions of a single concentration. This study has taken into account three different ions with a concentration ranging from 2 to 22% w/w.

It is important to stress that this study used intact shale samples while other studies have used clay minerals. The use of intact shale samples is more beneficial and relevant to the drilling industry as it helps us mitigate shale swelling and wellbore instability when drilling reactive shales.

I plan to further expand this work in the future to include the following research topics:

• The impact of temperature and time on the diffuse double layer development when shale interacts with highly concentrated ionic solutions.

• The impact of changes in a diffuse double layer on shale’s porosity and permeability as shale interacts with highly concentrated ionic solutions.

Conclusions & recommendations

Debye Hückel lengths (κ⁻¹) were calculated using Eq. (1) and compared with swelling tests on two shale samples using two monovalent ionic solutions (NaCl and KCl) and one divalent ionic solution (CaCl₂) at concentrations ranging from 2 to 22%w/w. There exists a ‘critical concentration’ below which the Debye Hückel length equation works. Above the critical concentration, the validity of the Debye Hückel length equation might be in question. The critical concentration is different for all ions and depends on ionic valence, hydrated ion diameter and clay type. In this work, it was shown that osmotic water flows out of shale causes shale shrinkage, which could translate into a decrease in the diffuse double layer thickness. On the other hand, associated water transfer into shale by means of diffusion osmosis leads to shale expansion and swelling, which could be interpreted as an increase in the diffuse double layer thickness. The role of ionic invasion into shale is not well understood but I believe that excessive ionic invasion into shale increases electrostatic repulsive forces between similar charges which could further expand the diffuse double layer.

Results from this work could help us mitigate shale swelling and wellbore instability when drilling reactive shales. The use of highly concentrated salt solutions to osmotically withdraw water out of shale to combat shale swelling and hydration may not be appropriate and could lead to bigger problems as it expands the diffuse double layer thickness and eventually causes more swelling and instability. It is highly recommended to use salt solutions at lower concentrations to reap the benefits of chemical osmosis and avoid excessive induction of ionic diffusion and diffusion osmosis. More work needs to be done to fully understand the role of excessive ions concentrations on the diffuse double layer thickness (κ⁻¹).