Impact of karstification in trapping mechanisms of CO₂ storage

Abstract

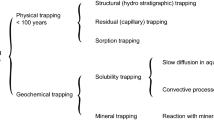
A carbonate-depleted carbonate gas field located offshore Sarawak has been identified as potential candidate for CO₂ sequestration site in conjunction with another high CO₂ gas field development for commercialization efforts. The field has undergone a feasibility study to evaluate potential geochemical reactions specifically on trapping mechanisms and storage capacity associated with CO₂ injection. A detail 3D reactive transport modelling study was conducted to quantify on the four different trapping mechanism: structural, residual, solubility, and mineral trapping during and post-injection. The model was developed by first converted the available field history matched black oil simulation model into compositional 3D model, in which CO₂ is treated as separate component in the reservoir through the production and injection processes. The study covered 22 years of gas production history forecast followed by 27 years of injection and 1000 years of post-CO₂ injection in the gas column reservoir. The results show that the field has potential to store and sequestrate CO₂ up to for 79% structural trapping, 19% residual trapping, 3% solubility trapping and no mineral trapping after 1000 years of post-injection period.

Introduction

A storage in depleted gas reservoirs is one way to reduce the increasing greenhouse gases in the atmosphere. Any large scale of CO₂ injection involves a variety of coupled physical and chemical processes including multiple fluid flows, solute transport, and chemical reactions between the resident fluids and reservoir minerals. To date, most of previous studies has focused on the reactivity and trapping mechanisms during post-injection of several thousand years (Gallo et al. 2006; Lindeberg and Wessel-Berg 1997, 2002, 2003; Liu et al. 2012; Pruess and García 2002). However, none of the previous study has discussed about the impact of karstification in the carbonate field. Thus, this study focuses on detailed geochemical impact in terms of trapping mechanisms due to the presence of karstification in the carbonate field. The main objectives of this study are:

• To obtain on the kinetic rate parameters from laboratory-calibrated model for 3D coupled model.

• To study on the short- and long-term reactions due to CO₂ injection in carbonate reservoir.

• To obtain on the CO₂ storage trapping mechanism during and post-injection of CO₂ in carbonate reservoir.

• To study on plume migration of CO₂ in the presence of heterogeneity in the carbonate reservoir.

Background

A carbonate build-up platform in the Central Luconia Province is located 260 km NW of Bintulu. The field was discovered in 1970, when X-1 well was drilled and appraised by X-2 well in 1991. Structurally, the field is a high relief carbonate build-up and forms part of the Mega Platform complex comprised of other two carbonate fields with a common regional aquifer (Fig. 1).

Fig. 1

Carbonate platform build-up in Mega Platform Complex which the reservoir being study is located

The main carbonate reef build-up for field is concentrated in the south east due to the prevailing SE-NW paleowind direction at the time of deposition. The depositional environments in this location are the rim-reef cores, fore-reef to back-reef, where generally the primary porosity properties are good. Platform progradation and sediment shedding occurred in the downwind position towards the NW, where the depositional environment is mainly lagoonal. Generally, the reservoir properties are believed to deteriorate in this area. However, due to diagenesis, much of the porosity being attributed to secondary porosity enhancement, making the lagoonal reservoir properties superior compared to in the reef facies.

The reservoir porosity in the gas zone ranges from 15 to 32%, while the core permeability derived from well ranges between 9 and 200 mD. Production test interpretations indicate higher permeability of 200–480 mD probably due to karsts or fractures. The field has a strong underlying aquifer support.

Materials and methodology

Geochemical data

The system was modelled using the initial formation brine composition from analogue field as in Table 1 and the primary mineral assemblage from the study field as input data. (Table 2).

Table 1 Initial formation brine taken from analogue carbonate field

Table 2 Mineralogy composition

Kinetic batch modelling

Prior to simulating reactive transport for the carbonate reservoir, a batch geochemical model of water–rock interaction was performed to generate an aqueous-phase chemical composition approaching the composition of typical formation brine. This was done by equilibrating the initial formation brine composition as in Table 2 with the presence of the primary minerals at depth of 6079ft as listed in Table 1.

The initial brine composition was equilibrated with the mineralogy of the study field mineralogy (Table 2), and the resulting brine composition (Table 3) was used as a starting point for subsequent modelling in this study. From XRD analysis from the selected well in Table 1, the mineralogy composition (in average wt%) used in the model are as follows:

• Calcite–71.0 wt % to 92.9 wt % (average 83.8 wt %)

• Dolomite–0.4 wt% to 2.7 wt % (average: 1.8 wt%)

• Siderite–0.8 wt% to 1.0 wt% (average 0.9 wt%)

• K-feldspar–1.1 wt%—4.9 wt% (average: 2.4 wt%)

• Quartz–< 1.5 wt% (average: 0.5 wt%)

• Clay minerals–< 12.5 wt % (average: 6.6 wt%)

Table 3 Initial formation water for laboratory-calibrated model

After the equilibration of the formation water and mineralogy, a total of eight aqueous components were used as initial formation water in the model (Table 3). Simulations were for three-dimensional reactive transport modelling and was simulate at iso-thermal conditions of 275°F and average reservoir pressure of 2538 psi. Since the reservoir is dominantly dominated by carbonates, the model was simplified using calcite (0.90 of volume fraction) and dolomite (0.10 of volume fraction) composition. The model systems chosen were the initial formation water composition, and the primary mineral assemblage consists of Calcite (Volume fraction: 90%) and Dolomite (Volume fraction: 10%) from the aquifer. Laboratory-calibrated model was used to obtain on kinetic rate and reactive surface areas parameters of minerals for the field.

Kinetic rates

Dissolution and precipitation of minerals in the system were kinetically controlled. The rates of mineral dissolution and precipitation rates were derived from (Lasaga et al. 1995):

$$rate_{{m}} = A_{m} k(T)_{m} (a_{{H^{ + } }} )^{n} \left[ {1 - \left( {Q_{m} /K_{m} } \right)} \right]$$

(1)

where the subscript m is the mineral index, and ratem is the dissolution/precipitation rate(m/s), Am is the reactive surface per kg water (unit), k(T) is the temperature dependent rate constant, aH⁺ is the proton activity, n is the order of the reaction (0 ≤ n ≤ 1), Km is the equilibrium constant for the mineral water reaction written for the dissolution of 1 mol of mineral and Q_m is the reaction quotient. The last term in Eq. 1 takes into account that the rate of reaction depends on how far the system is from chemical equilibrium, that is, the degree of over- or under-saturation. The rate constants in Eq. 2 for all minerals were extrapolated to the field condition temperatures of 348.15 K from reported rate constants at 298.15 K using the Arrhenius relation:

$$k(T) = k_{25} \exp \left[ { - E_{a} /R(1/T - 1/298.1)} \right]$$

(2)

where E_a is the activation energy (J/mol), k₂₅ is the rate constant at 250 °C (mol/m²s), R is the universal gas constant (8.314 J/mol K) and T is the temperature (K). The rate constants at 298.15 K (k₂₅) and parameters for the calculation of reaction rates for all minerals were taken from the laboratory-calibrated model as discussed in the subsequent section.

Precipitation of secondary minerals depends on nucleation, Ostwald ripening, crystal growth processes, and reactive surface (Plummer 1978; Steefel and Cappellen 1990). Due to coating, interaction with the minerals is generally expected to occur only at selective sites of the mineral surface and the actual reactive surface area could be between one and three orders of magnitude less than the surface roughness based surface area (Lasaga et al. 1995). To account for these effects, a surface roughness factor of 10 was incorporated and defined as the ratio of the true (BET) surface area to the equivalent geometric surface area.

Reactive surface areas

The composition of the mineral assemblages was taken from samples M3 carbonate field. The reactive surface areas for calcite and dolomite were calculated using geometrical calculation method due to unavailability of BET measurement in the laboratory (Table 4). Reactive surface areas were calculated using geometrical calculation—based on assumption of idealized geometry of mineral grains (spherical grains with grain diameters of 3.3 × 10^–5).

Table 4 The reactive surface areas for calcite and dolomite

Three-dimensional (3D) reactive modelling

Reactive transport model was taken from static model of 300 thickness with three (3) CO₂ injectors well and ten (10) gas producers. The model consists of 117,024 grid blocks with active cells of 91,475. Since the model was generated from static model, the model is heterogeneous in terms of the rock properties (porosity and permeability). The static model is then converted into static model in CMG before the model was run with geochemistry inputs (initial formation water, minerals composition, kinetic rate, and reactive surface areas) for geochemical modelling study. The simulation was run for 27 years of injection period and post-injection of 1,000 years.

Results and discussion

The results from kinetic batch modelling (laboratory-calibrated model) and three-dimensional reactive transport modelling for the study carbonate field are presented in this section.

Kinetic batch laboratory-calibrated model

The study used calibrated experimental batch model to analyse and interpret CO₂-injection-induced carbonate dissolution phenomena from pore to score scale. The same approach on using laboratory-calibrated models to obtain on the kinetic rate and reactive surface areas parameters for full field/3D reactive transport modelling has been used by several authors in the literature to study on the geochemical reactions due to CO₂ injection in reservoirs.

Static ageing experiment was conducted in the laboratory to evaluate on the effects of CO2 injection on the kinetic reaction and mineralogy changes after 45 days (Fig. 2). The sample used for laboratory-calibrated model is the ones from aquifer zone, which is at depth 6079 ft. The sample is submerged into synthetic brine with supercritical CO₂, S_CO2, injection under reservoir pressure and temperature (2900 psi and 275F).

Fig. 2

Static ageing experiment set-up. The experiment was conducted for 45 days using synthetic brine created to mimic the real formation brine of the carbonate reservoir being studied

The changes of main components ((Ca²⁺, Mg²⁺, K⁺, Na⁺) of formation brine components were measured using Inductively Coupled Plasma (ICP) measurement. The increases in Ca²⁺ as shown in Table 5 indicate calcite dissolution due to CO₂ injection. The pre- and post-sample analysis on porosity changes are conducted using Digital Core Analysis (DCA), where the results shown very insignificant changes in porosity, which is 0.47%. In addition, XRD analysis shown very minor changes in calcite mineral and other minerals, which is less than 0.5%.

Table 5 ICP analysis results for main components for pre- and post-static ageing experiment

The calibrated models using static ageing experiments conditions are developed to get kinetic rate and reactive surface area input data for full field/3D reactive transport modelling. The input parameters model for calibrated model used are shown in Table 6. The reactive surface area is calculated using geometrical calculation, and it is fixed in the model. Rate constants were adjusted to fit the model with the experimental data to match with Ca²⁺ changes in concentration for pre- and post-experiments. However, the laboratory data for ICP measurement on Ca²⁺ concentration changes is insufficient as there is only two data points to be matched (Fig. 3). The resulting kinetic rates for calcite and dolomite obtained from the calibrated models are shown in Table 7.

Table 6 Input parameters model for calibrated model

Fig. 3

Laboratory-calibrated model plot. The kinetic batch model was developed based on static ageing experiment. The model was fit using trying and error method from Ca²⁺ concentration data obtained before CO₂ injection (initial formation brine) and after 45 days of reactions of static ageing experiment

Table 7 Laboratory-calibrated model input data for 3D full field reactive transport modelling

3D reactive transport modelling

Short-term fate (27 years of injection to 100 years of post-injection)

Gas saturation

After the injection, the vertical flow of CO₂ rich gas is influenced by buoyancy. This is due to the difference in the density and viscosity of CO₂-rich gas and brine. The smaller viscosity of CO₂-rich gas compare to brine causes hydrodynamic instabilities. Eventually, counter current flow occurs as the gas flows upward and the brine downward. The profile of CO₂ mole fraction in the model domain during 27 years of injection and 100 years of post-injection is plotted in Figs. 4 and 5. The CO₂ plume size is illustrated using gas mole fraction of CO₂. The significant gas front saturation phase of injected CO₂ propagates laterally to the West of the injection well giving the high concentration of CO₂ saturation layer in gas zone.

Fig. 4

Gas saturation after 27 years of injection. The spatial distribution of CO₂ dissolved in aqueous phase at time of simulations given in terms of mole fractions

Fig. 5

Gas saturation after 100 years of injection. The spatial distribution of CO₂ dissolved in aqueous phase at time of simulations given in terms of mole fractions

Changes in pH

Following the injection of CO₂ into the system, the pH immediately decreased from 7.4 to 6.3 and thereafter remain the same until end of injection period. The initial fugacity, fCO₂ controls this available CO₂ in the system and consequently the evolution of the pH over the course of the reaction. The dissolution and precipitation of the minerals, discussed below (Fig. 6), reflect the consumption of the acidic CO₂ by CO₂-brine-mineral reactions. These geochemical reactions result in an increasing pH at later period. A higher fco₂ increases the amount of dissolved CO₂ in the brine and as a result increase the extent of mineral dissolution. Minerals such as calcite dissolve rapidly, leading to an increase in pH.

Fig. 6

pH changes near to one of CO₂ injector well before and during CO₂ injection period of 27 years. There is a drop in pH when CO₂ injection starts in 2026

Mineral dissolution/precipitation

Buffering occurs when dissolved CO₂ reacts, for instance, with reactive carbonates such as calcite and dolomite (Reaction 1until 3). These reactions may provide sufficient buffering capacity (via HCO₃⁻ alkalinity) to resist drastic changes in pH. The presence of reactive carbonates such as calcite in a host reservoir will have a major impact on how the chemical reactions evolve during injection of CO₂. If CO₂ dissolved into brine is in equilibrium with carbonate minerals, the total amount of dissolved inorganic carbon (CO_2(aq), HCO₃⁻_(aq), CO₃²⁻_(aq)) in the host reservoir.

Reaction 1

$${\text{H}}_{2} {\text{O}} + {\text{CO}}_{2} \leftrightarrow {\text{H}}_{2} {\text{CO}}_{3} \leftrightarrow {\text{H}}^{ + } + {\text{HCO}}_{3}^{ - }$$

Reaction 2:

$$\mathop {{\text{CaCO}}_{3} }\limits_{{{\text{Calcite}}}} + {\text{H}}^{ + } \leftrightarrow {\text{Ca}}^{2 + } + \; + {\text{HCO}}_{3}^{ - }$$

Reaction 3:

$$\mathop {{\text{CaMg}}({\text{CO}}3)_{2} }\limits_{{{\text{Dolomite}}}} + {\text{H}}^{ + } \leftrightarrow {\text{Ca}}^{2 + } + {\text{Mg}}^{2 + } + {\text{HCO}}_{3}^{ - }$$

After 27 years injection of CO₂ into the aquifer, the supercritical fluid is in contact with the residual brine in the gas column. As a result, it forms H₂CO₃, a weak acid that almost immediately dissociates into hydrogen and bicarbonate. The low pH during injection of 27 years with CO₂ causes the brine to become highly under saturated with respect to carbonates especially calcite present in the carbonate reservoir. The main carbonates that dissolve progressively are calcite. The amounts are multiplied is observed in the injected plume or at edges of the plume, where gradients in pH is greatest. The corresponding changes in calcite volume fraction are shown in Fig. 7. From the figure, zone above the Gas Water Contact (GWC) which the CO₂ injector located shows very small changes in terms of calcite dissolution. For zone below GWC, there is no dissolution of calcite occurs due to the absence of CO₂ in this zone. There is a thin layer of high dissolution zone above the GWC of the aquifer. This is the plume region, with a gradient to lesser dissolution below this boundary during short term of reactions (less than 100 years).

Fig. 7

Calcite volume changes near to one of CO₂ injector well before and during CO₂ injection period of 27 years. There is dissolution of calcite occurs when CO₂ injection starts in 2026

Changes of porosity

Temporal changes in porosity due to mineral dissolution and precipitation can affect fluid flow. The dissolution of minerals such as calcite changes the formation porosity. Then, changes in this property cause the changes in the fluid flow patterns. When this occurs, there is an additional pore space to accommodate brine and CO₂. The changes of porosity were calculated from changes in volume fractions of minerals caused by the minerals reactions at each time step of running simulations according to Eq. 3 below:

$$\Delta \emptyset_{t} = \left( {1 - \frac{{\mathop \sum \nolimits_{i} n_{i,t} V_{i,x} }}{{V_{total} }} } \right) - \emptyset_{t} = 0$$

(3)

where, $\emptyset_{t = 0}$ is the initial porosity, $n_{i,t}$ is the moles of dissolved minerals $i$ at time of simulations, $V_{i,t}$ is the molar volume of dissolved minerals $i$ at time of simulations and $V_{total }$ is the total initial minerals volume of the system.

The changes in porosity affect permeability. Small increases in porosity will increase the permeability. This creates a migration pathway especially at the top of carbonate (cap rock) for CO₂ into the surface. Thus, an assessment of the change in porosity is very crucial to understand the migration pathway of CO₂ plume in the reservoir.

All the above reactions impact the porosity by changing of mineral volume due to dissolution and precipitation of minerals. In reservoir above the GWC zone, the delta porosity is very insignificant, which is with 0.03%. Zone below the GWC shows no changes in porosity due to the absence of CO₂ in this zone during CO₂ injection period of 27 years until end of 100 years of post (Figs. 8 and 9).

Fig. 8

Porosity changes above the GWC (near to CO₂ injection well) for 27 years of injection

Fig. 9

Porosity changes below the GWC during 27 years of injection

Long-term fate study (100–1000 years post-injection injection)

Upon CO₂ injection into the reservoir, the supercritical CO₂ migrates upward quickly due to the density differences. As a result, most of the supercritical CO₂ accumulated in this zone (Fig. 10). Over the years, the CO₂ dissolved, and the dissolved plume migrates downward due to the larger density of brine with CO₂ compared with the brine without CO₂. It was reported in Ennis King and Paterson, 2003 that the larger density of brine with CO₂ is approximately 10 kg/m³ higher compared with the brine without CO₂. The brine containing dissolved CO₂ in carried downward and is subsequently replaced by brine with less CO₂. This process is known as convective.

Fig. 10

Gas saturation after 100 years of post-injection. CO₂ plume migration migrates laterally to the west of the reservoir due to the presence of impermeable layer at the east zone of the reservoir

It is acknowledged that the role of convection mixing is crucial during the long-term CO₂ dissolution (Ennis-King and Paterson 2005; Linderberg 2002). This phenomena can been seen in Fig. 11, where at 300 years, the dissolve CO₂ started to have the push-down effect. The denser CO₂-saturated brine moves downward due to higher permeability zone due to karstification in the host reservoir (Figs. 12, 13, 14). The properties of the model were populated from the static model as in Fig. 14. At the end of 1000 years post-injection, the dissolved CO₂ is dominant in the aquifer zone. The same observation being made by Agartan et al. (2015). At the end of 1000 years post-injection, the dissolved CO₂ is dominant in the aquifer zone. However, due to the low permeability zone at the East part of the reservoir, there is no downward movement of heavily denser CO_2. (Fig. 14). Several other authors that observed the same findings which reported that vertical heterogeneity impact on the solubility trapping of CO₂ in the reservoir are tabulated in Table 8.

Fig. 11

Gas saturation after 300 years of post-injection. CO₂ plume migration migrates laterally to the west of the reservoir due to the presence of impermeable layer at the east zone of the reservoir

Fig. 12

Gas saturation after 500 years of post-injection. CO₂ plume migration migrates laterally to the west of the reservoir due to the presence of impermeable layer at the east zone of the reservoir

Fig. 13

Gas saturation after 1000 years of post-injection. CO₂ plume migration migrates laterally to the west of the reservoir due to the presence of impermeable layer at the east zone of the reservoir

Fig. 14

Impact of karstification in the carbonate reservoir on the convection/fingering effect at top of the reservoir

Table 8 List of literature and its key findings on effect of vertical heterogeneity/permeability on trapping mechanism

Changes in pH, minerals, and porosity

The geochemical evolution for long-term reactions is shown in Figs. 16, 17 plotting pH, changes in mineral abundance and porosity against time. The reactivity of long-term reactions is best interpreted using the evolution of pH. The evolution of pH is related to the amount of CO₂ dissolved in the brine. The evolution of pH and minerals changes for long-term reactions is shown in Figs. 15 and 16. It was no significant changes in the pH and mineral volume. In addition, there is very insignificant changes in porosity for 1000 years of post-injection, which is 0.0021% in porosity increase (Fig. 17).

Fig. 15

Evolution of the pH for the system with dissolved CO₂ in the carbonate rock. The simulations were first run for 27 years to account for the injection period followed by 1000 years to account for retention period. A significant drop of pH is observed after CO₂ injection into the reservoir. The dissolved CO₂ reacts with primary minerals, initially with calcite. The model was run with calcite mineralogy only as the study was simplified and calcite was chosen due to its fast kinetic rates compared to other minerals. The reactions with calcite leading to an increase in the pH and the pH stays constant after this period as all the minerals have reacted

Fig. 16

Minerals changes during 1000 years of post-injection. The simulations were first run for 27 years to account for the injection period followed by 1000 years to account for retention period. After the CO₂ injection, the dissolved CO₂ reacts with primary minerals, initially with calcite. The model was run with calcite mineralogy only as the study was simplified and calcite was chosen due to its fast kinetic rates compared to other minerals. The reaction with calcite is very small due to CO₂ injection

Fig. 17

Porosity changes during 1000 years of post-injection. The simulations were first run for 27 years to account for the injection period followed by 1000 years to account for retention period. After the CO₂ injection, the dissolved CO₂ reacts with primary minerals, initially with calcite. The model was run with calcite mineralogy only as the study was simplified and calcite was chosen due to its fast kinetic rates compared to other minerals. The changes of porosity observed in the model are very small after post-injection of 1000 years

Total amount of sequestered CO₂

The total amount of CO₂ stored in aqueous, gas, and solid phases over time during the injection period of 21 years in the reservoir is shown in Table 9. From this table, approximately 79% of injected supercritical CO₂ remains in gas phase over 27 years of injection. However, over long timescale the amount of supercritical (own phase), CO₂ decreases and CO₂ in the dissolved brine increases. The total amount of CO₂ sequestered is calculated by the changes in moles of carbon inventory multiplied by the molecular weight.

Table 9 CO₂ inventory for end of 27 years of injections and post-injection of 1,000 years

Conclusions

This study set out to explore the effects of injected CO₂ on geochemical reactions and fluid dynamics over geological timeframe of 1,000 years in the carbonate depleted gas reservoir. Kinetic batch modelling/laboratory-calibrated model was developed to obtain on kinetic rates and reactive surface areas that were used as an input data for 3D reactive transport modelling.

The main outcomes of the study are:

• Reactive transport modelling indicates that the geochemical processes in the reservoir is dominated by 79% structural trapping, follow by 19% residual and 3% solubility trapping.

• The CO₂ inventory for post-injection until 1000 years is tabulated in Table 9, which the solubility trapping is observed to increase after 1000 years of reactions.

• The results indicate that extent of trapping mechanisms and CO₂ plume migration are highly dependent on vertical reservoir heterogeneity which is the presence of karstification in the reservoir.

Limitation and recommendation for future studies are:

• The study predicts no mineral trapping as 1000 years of simulation is too short for the model to observe any precipitation of minerals. It is anticipating that mineral trapping would take place once the model system reaches super-saturate state, and these processes are very slow which this could only potentially occur over 10,000 years of reactions. It was anticipating that the trapping of CO₂ in minerals would be very minimum and will not jeopardize on any integrity issue of the storage.

• For future work, the same approach for up till 10,000 years of simulation period could be useful to assess the potential mineral trapping in carbonate depleted gas fields and its effect on integrity issues.