Introduction

Given the problem of multi-layer co-production in gas reservoirs, many domestic scholars have carried out relevant research on production allocation and co-production effect (Liu et al. 2020; Salvi and Panwar 2012; Sun et al. 2019). Based on percolation theory, Liu Qiguo et al. established the calculation model of production contribution of slicing by considering the wellbore reservoir effect and skin factor of each small layer (Qiguo et al. 2010). Yang Bo et al. proposed three simple calculation methods of production allocation based on field slicing test data and reservoir engineering method (A simple new method for rational production allocation of multi-layer commingled production wells [J]. Oil and gas well testing 2010). Xiong Yanli et al. used numerical simulation to compare single well multi-layer co-production and two well-slicing production in the same field (Yanli 2005). It is found that under the premise of no obvious geological difference between layers, it is suitable to adopt the development mode of multi-layer combined mining. Shao Changjin and others analyzed the sensitivity of formation-related parameters during multi-layer combined mining by using CMG software, which shows that the permeability and initial formation pressure of each layer have an important impact on the productivity of combined production (Sun et al. 2019).

With the development of coalbed methane exploration and development in recent years, it is found that more and more coalbed methane reservoirs have abundant tight pay zones besides coal pay zones (King 1990; Lefkovits et al. 1961; Larsen 1981). The main reason is that the adsorption pressure and desorption pressure are lower than that of the conventional coalbed, and the main reason is that the desorption pressure of the coalbed is lower than that of the conventional coalbed (Aly et al. 1994; Zhao et al. 2020). At present, there is little research on multi-layer combined production of coalbed methane reservoir at home and abroad. According to the characteristics of coalbed methane reservoir in China, this paper uses node analysis method to program iterative coupling calculation in wellbore and obtains the development performance characteristics and development effect of coalbed tight seam combined production gas well, which can provide the basis for the adaptability and effect of such multi-layer combined production.

Productivity formula and pressure drop mechanism of tight sandstone

Productivity formula of tight sandstone gas well

In order to simplify the difficulty of programming, it is considered that the tight gas reservoir layer is always in the quasi-stable state. Although the quasi-stable state is unstable, it can be regarded as a semi-stable state and can still be treated as a stable state (Li et al. 2021; Shanley et al. 2004; Sheikholeslami et al. 2021a, 2021b). The skin factors and non-Darcy flow of fluid are considered.

$$\psi - \psi_{wf} = \frac{{1.291 \times 10^{ - 3} q_{sc} T}}{Kh}\left( {\ln \frac{{0.472r_{e} }}{{r_{w} }} + S + Dq_{sc} } \right)$$
(1)

If the average formation pressure concept is used, the above equation can be transformed.

$$p_{R}^{2} - p_{wf}^{2} = \frac{{1.291 \times 10^{ - 3} q_{sc} \mu ZT}}{Kh}\left( {\ln \frac{{0.472r_{e} }}{{r_{w} }} + S + Dq_{sc} } \right)$$
(2)

When using the well-test data to determine the productivity equation of tight gas well, the above formula can be changed into the following form.

$$p_{R}^{2} - p_{wf}^{2} = \frac{{1.291 \times 10^{ - 3} q_{sc} T\mu Z}}{Kh}\;\left( {\ln \frac{{0.472r_{e} }}{{r_{w} }} + S} \right) + \frac{{2.828 \times 10^{ - 21} \beta \gamma_{g} ZTq_{sc}^{2} }}{{r_{w} h^{2} }}$$
(3)

The above formula is simplified by classic binomial method

$$A = \frac{{1.291 \times 10^{ - 3} T\mu Z}}{Kh}\left( {\ln \frac{{0.472r_{e} }}{{r_{w} }} + S} \right)$$
(4)
$$B = \frac{{2.282 \times 10^{ - 21} \beta \gamma_{g} ZT}}{{r_{w} h^{2} }}$$
(5)

where A is the coefficient of laminar term, and B is the coefficient of turbulent term.

Once coefficients are determined, the productivity equation of the well can be obtained.

$$q_{sc} = \frac{{ - A + \sqrt {A^{2} + 4B\Delta p^{2} } }}{2B}$$
(6)

According to the above formula, given a bottom hole flowing pressure, a corresponding surface production rate from the tight gas reservoirs can be calculated.

Pressure drop law of tight gas reservoir

Assuming that the gas reservoir has no connected edge water or bottom water, or the edge water or bottom water is fairly inactive, it is a constant volume gas drive gas reservoir (Welge 1952; Loucks and Ruppel 2007; Jang and Santamarina 2014; Zhao et al. 2021).

$$GB_{gi} = (G - G_{p} )B_{g}$$
(7)

By further simplifying the above formula, we can get the following results:

$$\frac{p}{Z} = \frac{{p_{i} }}{{Z_{i} }}\left( {1 - \frac{{G_{p} }}{G}} \right)$$
(8)

where GP is the cumulative production. According to the above formula, we can get the change of average formation pressure with the recovery of gas.

Productivity formula and pressure drop mechanism of coalbed methane

Production equation of gas and water in coal seam

As for the case of Gas–water two-phase flow in coal seam, productivity equations are given below (Mohaghegh and Ertekin 1991; Sun et al. 2018):

$$q_{g} = \frac{{K_{rg} (S_{w} )Kh(p^{2} - p_{wf}^{2} )}}{{1.291*10^{ - 3} \mu zT\left( {\ln \frac{{r_{e} }}{{r_{w} }} - \frac{3}{4} + S} \right)}}$$
(9)
$$q_{w} = \frac{{0.543K_{rw} (S_{w} )Kh(p - p_{wf} )}}{{B_{w} \mu_{w} \left( {\ln \frac{{r_{e} }}{{r_{w} }} - \frac{3}{4} + S} \right)}}$$
(10)

Pressure drop law of coalbed methane reservoir

As unconventional energy, coalbed methane has special properties different from other gas reservoirs. This also directly leads to the difference of coalbed methane production mode from other conventional gas reservoirs. There exists a period of dewatering in the initial stage of coalbed methane exploitation, during which the pressure drops rapidly and generally lasts for about one month (Aminian and Ameri 2009; Clarkson et al. 2009; Clarkson and Salmachi 2017; Dong et al. 2016). When the pressure drops below the critical desorption pressure, a large amount of gas will be released from the coal seam, and then, the coalbed gas saturation rises, and the water production gradually decreases. The material conservation law of coal seam is provided below.

$$\begin{aligned} W_{p} B_{w} + G_{p} B_{g} & = C_{g} Ah\phi (1 - S_{{wi}} )(P_{d} - \overline{P} ) + C_{w} Ah\phi S_{{wi}} (P_{d} - \overline{P} ) + Ah(1 - \phi )\frac{{V_{l} bP_{d} }}{{1 + bP_{d} }} \\ & \quad - Ah(1 - \phi )\frac{{V_{l} b\overline{P} }}{{1 + b\overline{P} }} \\ \end{aligned}$$
(11)

where, Swi—original water saturation of coal seam, dimensionless; Vl—Langmuir volume constant, i.e., the maximum volume of gas adsorbed per unit mass of coal sample; B— Langmuir pressure constant, MPa−1; Φ—porosity, dimensionless;

$$B_{g} = \frac{{ZTP_{sc} }}{{PT_{sc} }}$$
(12)

Only the conservation of matter of water is provided below.

$$W_{p} = \frac{{Ah\phi S_{wi} }}{{B_{wi} }} - \frac{{Ah\phi S_{w} }}{{B_{w} }}$$
(13)

Bwi—original volume coefficient of coal seam water, dimensionless;

Bw—volume coefficient of gas under current pressure, dimensionless;

Wp—cumulative surface water production.

The formula (13) is further simplified.

$$S_{w} = S_{wi} \frac{{B_{w} }}{{B_{wh} }} - \frac{{W_{p} B_{w} }}{Ah\phi }$$
(14)

Coupling calculation method for gas production performance of tight gas wells

Calculation method of wellbore pressure drop

A method for pressure drops calculation of horizontal, vertical, and arbitrary inclined pipe flow was put forward by some scholars, based on the experiments of water, air, and polypropylene pipes. In the specific calculation, the horizontal pipe flow is calculated first, and then, the inclined pipe flow is corrected by the inclination correction coefficient.

Assuming that the gas–liquid mixture has neither external work nor external work, the stable mechanical energy conservation equation of unit mass gas–liquid mixture is as follows:

$$- \frac{dp}{{dZ}} = \rho gsin\theta + \rho \frac{dE}{{dZ}} + \rho v\frac{dv}{{dZ}}$$
(15)

where

P—pressure;

Ρ—average density of gas–liquid mixture;

dE—mechanical energy loss per unit mass of gas–liquid mixture;

Z—flow direction;

Θ—the angle between the pipeline and the horizontal direction.

The above formula shows that the pressure drop of gas–liquid two-phase pipe flow is consumed in three aspects: potential difference, friction, and acceleration.

(1) Differential pressure gradient.

Pressure gradient consumed in the mixture hydrostatic head:

$$\left( {\frac{dp}{{dZ}}} \right)_{Hydrostatic} = \rho g\sin \theta = \left[ {\rho_{l} H_{l} + \rho_{g} \left( {1 - H_{l} } \right)} \right]g\sin \theta$$
(16)

where Hl—Liquid holdup, the volume fraction of liquid phase in a flowing gas–liquid mixture.

(2) Friction pressure gradient.

The pressure gradient to overcome the flow resistance consumption of pipe wall is as follows

$$\left( {\frac{dp}{{dZ}}} \right)_{Fraction} = \lambda \frac{{v^{2} }}{2D}\rho = \lambda \frac{G/A}{{2D}}v$$
(17)

where

λ—Flow resistance coefficient;

G—Mass flow rate of mixture.

(3) Acceleration pressure gradient.

Pressure gradient consumed induced by kinetic energy change:

$$\left( {\frac{dp}{{dZ}}} \right)_{Acce} { = }\rho v\frac{dv}{{dZ}}$$
(18)

Neglecting the compressibility of liquid and considering that the change of gas mass velocity is fairly small, and then, the following formula can be yielded:

$$\left( {\frac{dp}{{dZ}}} \right)_{Acce} { = }\;{ - }\;\frac{{\rho \upsilon \upsilon_{sg} }}{p}\frac{dp}{{dZ}}$$
(19)
$$\upsilon_{sg} = {{Q_{g} } \mathord{\left/ {\vphantom {{Q_{g} } A}} \right. \kern-\nulldelimiterspace} A}$$
(20)

(4) Total pressure gradient

$$- \frac{dP}{{dZ}} = \frac{{[\rho_{L} H_{L} + \rho_{g} (1 - H_{L} )]g\sin \theta + \frac{\lambda G\upsilon }{{2DA}}}}{{1 - \left\{ {\left[ {\rho_{L} H_{L} + \rho_{g} (1 - H_{L} )} \right]vv_{sg} } \right\}/P}}$$
(21)

If the pressure data, gas production, and water production at any point in the wellbore are known, the pressure distribution of the whole wellbore can be calculated iteratively.

Calculation process of gas production performance of combined production gas well

In the initial stage of production, the gas (water) production is constant, assuming a series of bottom hole flowing pressure of the lowest production layer. According to the productivity equation and pressure drop mechanism of the lowest layer, gas production and water production at this time are obtained. The wellbore pressure distribution program obtained by Beggs–Brill method is used to calculate the wellbore pressure of the upper production layer along the wellbore (Dong et al. 2016; Wen et al. 2017; Sun et al. 2020; Sheikholeslami and Jafaryar 2020). Similarly, according to the productivity equation and pressure drop mechanism of the reservoir layer, the wellbore pressure of the upper production layer is calculated. The gas production and water production at this time can be obtained by productivity equations. The gas production and water production in the next section of wellbore can be obtained by algebraic superposition at the next time. According to the wellbore pressure distribution program, the wellbore pressure of the upper production layer can be calculated upward along the wellbore. Calculate upward until the wellhead, and the wellbore production is the wellhead production. Compare the wellbore production with the constant gas (water) production in the production system. If the error falls into the acceptable range, the assumed bottom hole flow pressure is correct, and then the relevant data in the next step can be calculated. If the error between the two is large, it is considered that the assumed bottom hole flow pressure is not correct. At this time, it is necessary to re-assume the bottom hole flow pressure at that time and cycle the above steps until the error becomes reasonable.

Comparison of multi-layer combined production and gas production in single production layer

Optimization of production allocation for individual production of each layer

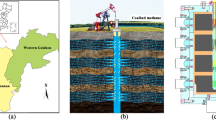
A well drilled through coal seam and two tight layers and the physical property parameters of each pay layer are shown in Table 1. Firstly, the optimal production allocation of each production layer is studied.

Table 1 Main parameters of each production layer
Full size table

For the tight layer, this paper selects different production systems, which are 5000 m3, 8000 m3.

According to Fig. 1 and Fig. 2, it is easy to know that when the fixed gas production rate in the production system is smaller, the stable production time of the well will be longer, but then the cumulative production in the prediction period will be smaller. Similarly, the higher the fixed production, the shorter the stable production time. Therefore, it is of great significance to select an appropriate production system for improving the efficient development of the well. In the figure above, it can be found that too low fixed production will lead to too low cumulative production, too high fixed production, and too short stable production time, so a reasonable production system should be between the two scenarios. When the fixed production is 10000 m3, it can be seen that the gas well can not only maintain a fairly long stable production time, but also the cumulative production in the prediction period is not much different from the fixed production of 15,000 m3. Therefore, the production system of the production layer is finally selected as the fixed production of 10,000 m3 per day.

Fig. 1
figure 1

Daily gas production of #1 layer under different production systems

Full size image
Fig. 2
figure 2

Cumulative gas production of #1 layer under different production systems

Full size image

The same method is adopted for two layers of tight sandstone (Fig. 3 and Fig. 4). They are 6000 m3, 8000 m3, 10,000 m3, 12,000 m3 and 14,000 m3. Finally, the optimal production system is obtained by two standards of stable production time and cumulative production.

Fig. 3
figure 3

Daily gas production of tight gas #2 layer under different production systems

Full size image
Fig. 4
figure 4

Cumulative gas production of tight gas #2 layer under different production systems

Full size image

According to the productivity prediction of the production layer and the above screening method, the optimized production system is fixed production of 12,000 m3. Under this production system, the production layer can maintain a certain stable production period, and the cumulative production in the forecast period is also higher.

Due to the special production system of coal seam, the water production is generally constant. The water in the coal seam is discharged in large quantities to achieve the purpose of rapid pressure reduction, and then, the production is carried out by setting the bottom hole flowing pressure. Therefore, in the design of coal seam production system, the daily water production should be set at 1 cubic meter per day at the initial stage. As depicted in Fig. 5, when the coal seam bottom hole flowing pressure is reduced to 1 MPa, the bottom hole flowing pressure should be set stable for production.

Fig. 5
figure 5

Daily water production of coal seam

Full size image

As depicted in Fig. 6 and Fig. 7, when the coal seam pressure is higher than the desorption pressure of the pay zone, the coal seam is in the period of water extraction, and the gas production is very little at this time. However, once the coal seam pressure is lower than the desorption pressure of the pay zone, a large amount of gas will be released from the coal seam, and the pay zone will usher in the peak of gas production. Then, the yield decreased slowly, which was shown as the slope of cumulative yield line decreased slowly.

Fig. 6
figure 6

Daily gas production of coal seam

Full size image
Fig. 7
figure 7

Cumulative gas production of coal seam

Full size image

Comparison of superimposed gas production between multi-layer combined production and individual production of each production layer

Through the above optimization of individual production system of each production layer, the predicted gas production value of each production layer under the optimized production system is superimposed to obtain the total gas production under the condition of individual production of each production layer. The gas production of multi-layer production is compared with the superimposed total gas production of each production layer. The working system of single well-combined production of multiple production layers is to determine the daily gas production of 15,000 m3/d, 18,000 m3/d, 20,000 m3/d, 22,000 m3/d, or 25,000 m3/d. When the pressure drop of bottom hole flow is 1.5 MPa, the bottom hole flow pressure is fixed for production. At the same time, considering the special situation of coal seam, the combined production well will be put into the corresponding production pump, and the depth of the pump is in the middle of coal seam. The water yield curve is shown in Fig. 8. The comparison of daily production of individual production superposition and combined production in each production layer is shown in Fig. 9.

Fig. 8
figure 8

Daily water production of commingled wells under different production systems

Full size image
Fig. 9
figure 9

Comparison of daily gas production of individual production superposition and combined production in each production layer

Full size image

As depicted in Fig. 10 and Fig. 11, according to the analysis of the gas contribution of each production layer, in the early stage of single well combined production, the contribution of tight 2# layer is the largest, and the coal seam has almost no contribution to the production capacity because of the dewatering period. With the development of production, the pressure of coal seam drops below the desorption pressure, but its gas production will increase slowly with the development of production in addition to the sudden increase in the production of single production layer, which is different from the separate mining of coal seam. In the late stage of commingled production, it can be seen from the figure that the gas production rate of tight layer #1 will be gradually higher than that of tight layer #2, making the gas production rate of this layer the largest.

Fig. 10
figure 10

The production system of single well combined production is 25000 m3/d, and the contribution gas of each production layer

Full size image
Fig. 11
figure 11

Percentage of gas contribution of each production layer when single well combined production system is 25000 m3/d

Full size image

In the initial stage, because each well maintained its own production system, the production began to be stable and then bulged because the coal seam pressure dropped below the desorption pressure, and the coal seam reaches the peak of gas production, driving the overall production bulge. It can be seen from Fig. 9 that since each layer is the optimal production allocation in the early stage of separate production, and the superimposed total daily gas production is large, the daily gas production in the later stage of production decreases rapidly. However, due to the different properties of each layer, some production layers are restricted in the early stage and do not release production capacity. With the change of pressure in the later stage, these production layers begin to contribute production capacity. This also makes the daily production of combined gas production in the later stage higher than the total daily production of individual production layers.

According to Fig. 12, it can be seen that the cumulative gas production of individual production layers is always higher than that of combined production. However, when the combined production and allocation production are high, such as 25,000 cubic meters per day, the cumulative gas production in the early stage is equivalent to that of individual production layers, and it is slightly lower than that of individual production layers in the later stage, which is only 2.56% lower. When the combined production is low, such as 18,000 m3/d, the cumulative gas production in the middle stage is lower than that in the superposition of individual production layers, but the cumulative gas production in the later stage increases greatly. If the combined production time can be very long, the cumulative gas production under different combined production systems is almost the same. Considering the impact of payback period, the work system of large allocation is the best. Therefore, for this example, the reasonable combined production is 25000 m3/d. Although different types of production layers are combined mining, it has little impact on the productivity of each production layer, so it is still favorable to adopt the method of combined mining for practical development.

Fig. 12
figure 12

Comparison of cumulative production of individual production and combined production in each layer

Full size image

Summary and conclusions

(1) Different from the common analysis method of production system considering single layer production, the gas production of each layer in multi-layer production cannot be directly evaluated by the intersection of inflow and outflow curves in the node analysis method. This is because when multiple layers are produced at the same time, the physical properties of each layer are different, so the iterative method should be used to calculate the gas production performance. According to the iterative coupling calculation method provided in this work, the gas and water production of production layer at any time can be obtained. Combined with the production performance analysis method of gas wells with multiple production layers and the calculation formula of pressure change under the condition of constant gas volume, the pressure performance of each layer of multi-layer commingled production wells can be predicted, so as to analyze the production performance of gas wells in the prediction period.

(2) According to a series of analysis in this paper, under suitable conditions, there is little difference between single well multi-layer mining and multi-well slicing-mining, the cumulative production difference in the prediction period is only 2.56%, but the development cost is huge, and the stable production time of single well multi-layer mining is longer than that of each production layer. Hence, single well multi-layer mining is adopted. Single well multi-layer mining is no doubt the first choice to realize the high-efficiency development of laminated mining.