Introduction

According to estimates by the U.S. Energy Information Administration (EIA), China’s technically recoverable tight oil resources amount to 44.8 × 108 t, ranking third in the world (Zou 2011). Among them, the Chang 7 reservoir in the Ordos Basin is an unconventional oil resource with source-reservoir symbiosis and is rich in resources (Yang et al. 2013; Zou et al. 2013; Wang et al. 2020; Yang et al. 2019). By the end of 2020, tertiary reserves will reach more than 1.5 billion tons, and resources will reach tens of billions. The area is mainly composed of continental clastic rock deposits with complex lithology, silt sandstone with a fine-grain size, poor physical properties, dense reservoirs, and a complex microscopic pore structure (Feng et al. 2013). The porosity of the oil layer group ranges from 4.0 to 12.9%, with an average of 7.4%; the permeability ranges from (0.01–1.55) × 10–3 μm2, with an average of 0.1 × 10–3 μm2. Judging from the national standard of the shale oil geological evaluation method (GB-738718-2020) proposed by Zou Caineng et al. the Chang 7 reservoir in the Ordos Basin has typical shale oil geological characteristics. In recent years, tight oil and shale oil (formation pressure coefficient generally greater than 1.3) in North America and other regions have been developed using volumetric fracturing depletion for horizontal wells. Under the background of high oil prices, these methods have obtained good economic benefits (Hu et al. 2018). However, the problem is that the initial decline is large (reaching 50% or more), and the recovery rate is low. Compared with foreign tight oil and shale oil, the largest difference in the Chang 7 reservoir in the Ordos Basin is that the formation pressure coefficient is lower, generally between 0.6 and 0.85. Compared with conventional oil reservoirs, the investment is very large. The developmental benefits of the project require more detailed work on geological evaluation and classification of the source.

Determination of the classification evaluation parameters of the Chang 7 oil group

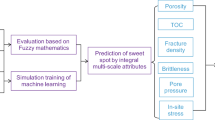
Developmental practice of unconventional petroleum resources such as tight oil and shale oil in the world shows that the distribution of oiliness on the plane, distribution pattern of oil layers in the vertical direction, in situ stress characteristics of the reservoir, rock brittleness and fracture characteristics are important parameters of unconventional petroleum resource developmental technology policy formulation and reservoir fracturing reformation (Zhang et al. 2015; Li et al. 2020; Zou et al. 2015). Therefore, to standardize and guide the development of the Chang 7 oil group in the Ordos Basin and provide a basis for the optimization of favorable target areas, developmental technology policy formulation, and reservoir fracturing, it is urgent to establish an evaluation method for the classification of the Chang 7 oil group in the Ordos Basin. From a literature survey, there are many studies on the reservoir characteristics of the Chang 7 reservoir in the Ordos Basin (Yao et al. 2013; Ju et al. 2020; Zou 2011; Zhu et al. 2014), but less work has been done on the classification of reservoir quality from the perspective of the integration of geology and engineering. Therefore, according to the geological characteristics and developmental characteristics of using horizontal well volume fracturing, quasi-natural energy development, and that considering only the permeability and oil content cannot accurately reflect differences in reservoir quality, a classification of the Chang 7 reservoir group in the Ordos Basin is proposed. The evaluation method solves the problem that the existing evaluation methods cannot accurately divide quality differences of the Chang 7 reservoir in the Ordos Basin to provide a reference for the later optimization of favorable areas, horizontal well developmental patterns, and artificial fracturing parameter optimization, which will ultimately improve developmental benefits.

Selection of classification evaluation parameters

On the basis of a previous literature research, in view of the reservoir characteristics, seepage characteristics and previous developmental practices of the Chang 7 oil group, according to the typical, easy-to-access, and strong operability evaluation parameter selection principle, the oil saturation, average pore throat radius, longitudinal structural coefficient of the oil layer, gas-oil ratio, brittleness index, and minimum horizontal principal stress are selected as the evaluation parameters to establish a comprehensive evaluation parameter system.

  1. (1)

    The oil saturation content (So) is the most important index for evaluating the oiliness of the Chang 7 oil group, and it is also the basis for profitable development. In actual mine applications, if core test oil saturation data are lacking, logging can also be used to explain the oil saturation or gas measurement total hydrocarbon value instead of showing the difference in oiliness.

  2. (2)

    The average throat radius (ra) not only reflects the microscopic pore structural characteristics of the Chang 7 oil group but is also an important control factor for seepage capacity.

  3. (3)

    The longitudinal structural coefficient of the oil layer (LSE) is a comprehensive reflection of the longitudinal oil layer distribution characteristics of the Chang 7 oil layer group. It mainly reflects the difference in the thickness and combination characteristics of the oil layer in the vertical direction. It is of great significance in evaluating the effect of horizontal well development and adopting reasonable well developmental types.

  4. (4)

    The gas-oil ratio (Go) refers to the amount of natural gas dissolved per unit volume or weight of crude oil under the original formation conditions. It is the most important energy source for the development of quasi-natural energy in the Chang 7 oil group.

  5. (5)

    The brittleness index (BI) reflects the difficulty of forming a complex fracture network by rock fracture in the reservoir.

  6. (6)

    The minimum horizontal principal stress (\(\sigma_{h}\)) is the minimum pressure at which the reservoir rock deforms and fractures along the plane direction under the action of an external force on the formation and reflects the difficulty of rock fracturing.

This evaluation parameter system combines key parameters, such as oiliness, seepage characteristics, initial energy, and rock mechanical characteristics, and can effectively reflect the difference in sweetness development of the Chang 7 oil group.

Determination of individual evaluation parameters

Oil saturation

The test method refers to the industry standard SY/T5336-2006 for core analytical methods. Thus, the oil saturation data obtained by core analysis and testing are mainly used, and corrected logging is used to interpret the oil saturation data (Table 1) for some areas where experimental tests are relatively lacking.

Table 1 Evaluation parameter values
Full size table

Average pore throat radius

The storage space in the rock is a complex three-dimensional pore network system, which can be divided into two basic units: pores and throats according to the role they play in the process of fluid storage and flow. In this system, the relatively swelling part that is surrounded by framework particles and plays a major role in fluid storage is called pores (narrow sense). Other relatively narrow parts that have little effect in expanding the pore volume but play a key role in the formation of communication pores become throats. Therefore, the average pore throat radius is obtained through the measurement of the rock capillary pressure curve (Table 1). The test method refers to the national standard GB/T29171-2012.

Longitudinal structural coefficient of the oil layer

The longitudinal structural coefficient of the oil layer represents the longitudinal heterogeneity of the oil layer and is related to the thickness of a single oil-bearing sand body, thickness of the total oil layer, number of oil layers, thickness of the largest oil interval, and ratio of sand to land. The thickness of a single oil-bearing sand body refers to the thickness of an oil-bearing sand body formed by a single ultrashort-term cycle (single layer), connected internally, and with a more continuous seepage barrier or part of the sand-sand contact interface. There are argillaceous barriers with a stable thickness distribution and good continuity between different sets of oil-bearing sand bodies, generally two meters and above, which is an important basis for dividing a single set of oil-bearing sand bodies. The total oil layer thickness refers to the sum of the thicknesses of a single set of oil-bearing sand bodies, and the number of oil layers refers to the number of a single set of oil-bearing sand bodies, which is specifically defined as:

$${\text{LSE}} = \frac{{oh_{\max } \times n_{{\text{o}}} \times sh}}{{(oh_{1} + oh_{2} + oh_{3} + \cdots oh_{n} ) \times fh}}$$
(1)

In the formula, LSE is the longitudinal structural coefficient of the oil layer; oh is the thickness of a single oil layer, m; n0 is the number of oil layers, piece; sh is the thickness of the sandstone, in m; and fh is the thickness of the formation, m.

According to the statistics of the relevant parameters of the oil layer where the sample is located, the value of the longitudinal structural coefficient of the oil layer is calculated by substituting the formula (Table 2).

Table 2 Calculation table of longitudinal structure coefficient
Full size table

Gas-oil ratio

The original gas-oil ratio, also known as the original dissolved gas-oil ratio, refers to the amount of natural gas dissolved per unit volume or weight of crude oil under the original formation conditions, and its unit is m3/m3 or m3/t. The original gas-oil ratio is an indicator of the amount of natural gas dissolved in crude oil, that is, the solubility of natural gas under this condition. The data source is thus mainly obtained through the formation crude oil test, and part of the data is the production gas-oil ratio (Table 1). The original gas-oil ratio test method refers to the industry standard SY/T5542-2000 for the physical properties of formation crude oil. When the original dissolved gas-oil ratio data are lacking, the produced gas-oil ratio data can also be used to replace the original gas-oil ratio. The production gas-oil ratio refers to the ratio of the first-stage separator gas production to the tank oil production (20 °C) under standard conditions, and its unit is m3/m3 or m3/t, which can be obtained through the oil well test or statistics of production data of oil wells.

Brittleness index

Rock brittleness theory is a comprehensive manifestation of Poisson's ratio and Young's modulus. The brittleness index based on rock mechanical characteristics can be obtained by taking the average of the two. The brittleness index calculation based on rock mechanical parameters calculates the Young's modulus and Poisson's ratio in the rock mechanical parameters with 50% weights. Among them, Poisson's ratio reflects the fracture ability of the rock under the action of an external force, and Young's modulus reflects the supporting ability of the rock after the fracture. The combination of different Young's moduli and Poisson's ratios indicates that the rock has different brittleness. The higher the modulus and Poisson's ratio are, the stronger the brittleness of the rock, and the easier it is to form complex fractures during the fracturing process. The brittleness index is calculated according to the empirical formula (Yang et al. 2014):

$${\text{BI}} = \frac{\Delta E + \Delta \mu }{2} \times 100$$
(2)

Among them:

$$\Delta E = \frac{{1.45 \times E \times 10^{ - 4} - 1}}{6}\quad \Delta \nu = \frac{0.4 - \mu }{{0.4 - 0.15}}$$

In the formula, BI is the brittleness index, %; ΔE is the normalized static Young's modulus, dimensionless; \(\Delta \nu\) is the normalized static Poisson's ratio, dimensionless; E is the static Young's modulus, MPa; and \(\nu\) is static Poisson's ratio, dimensionless.

The static Young's modulus and static Poisson's ratio can be measured based on laboratory experiments and can be calculated based on logging data.

Using density logging, array acoustic wave or dipole acoustic wave measured longitudinal wave time difference, shear wave time difference, and other data, the dynamic Young's modulus and dynamic Poisson's ratio of rock mechanical parameters can be calculated by the Po-Young method (Xu et al. 2014):

$$E_{{\text{d}}} = \frac{{\rho_{{\text{b}}} }}{{\Delta t_{{\text{s}}}^{2} }}*\left( {\frac{{3\Delta t_{{\text{s}}}^{2} - 4\Delta t_{p}^{2} }}{{\Delta t_{{\text{s}}}^{2} - \Delta t_{p}^{2} }}} \right)*10^{9}$$
(3)
$$\nu_{{\text{d}}} = \left( {\frac{{\Delta t_{{\text{s}}}^{2} - 2\Delta t_{p}^{2} }}{{2(\Delta t_{{\text{s}}}^{2} - \Delta t_{p}^{2} )}}} \right)$$
(4)

In the formula, Ed is the dynamic Young's modulus, MPa; \(\rho_{{\text{b}}}\) is the rock bulk density, g/cm3; \(\Delta t_{{\text{s}}}\) is the shear wave time difference of the rock, μs/m; and \(\Delta t_{p}\) is the rock longitudinal wave time difference, μs/m. \(\nu_{{\text{d}}}\) is the dynamic Poisson's ratio, dimensionless.

When using logging data to determine the above parameters, it is necessary to have longitudinal wave time difference, shear wave time difference, and density logging data at the same time. In oilfield development, exploration wells and evaluation wells generally test longitudinal wave time differences and shear wave time differences at the same time, but conventional development wells generally test P-wave time lags. To test the shear wave time difference, the following method can be used to calculate the shear wave time difference in this case.

We analyse the relationship between the shear wave time difference and longitudinal wave time difference according to the mine field statistics. For the Chang 7 oil group, through statistical regression of the exploration wells and evaluation wells that have been tested for rock bulk density and longitudinal wave, it is found that there is a good relationship between the shear wave time difference and longitudinal wave time difference and between the rock volume density and longitudinal wave time difference:

The relationship between the shear wave time difference and longitudinal wave time difference is:

$$\Delta t_{{\text{s}}} = 2.642\,\Delta t_{p} - 215.3$$
(5)

The relationship between rock volume density and longitudinal wave time difference is:

$$\rho_{{\text{b}}} = - \,0.0031\,\Delta t_{p} + 3.2693$$
(6)

Young's modulus and Poisson's ratio are required to calculate the rock brittleness index, but the Young's modulus and Poisson's ratio calculated using logging data are dynamic and need to be converted into static Young's modulus and Poisson's ratio. Conversion is according to the empirical formula:

$$E = (1.494\,E_{{\text{d}}} /10^{ - 4} - 4.076) \times 10^{4}$$
(7)
$$\nu = - \,0.894\,\nu_{{\text{d}}} + 0.478$$
(8)

In the formula, E is the static Young's modulus, MPa; and \(\nu\) is the static Poisson's ratio, dimensionless.

These data are mainly calculated based on logging-related parameters (Table 3).

Table 3 Calculation table of brittleness index
Full size table

Minimum horizontal principal stress

The internal stress stored in the Earth's crust is called ground stress. This is due to the vertical and horizontal movement inside the crust and other factors that cause the force per unit area inside the medium. The three-dimensional in situ stress model is commonly used to describe the in situ stress. One of the principal stresses is basically vertical, called the vertical stress, which is represented by the symbol \(\sigma_{v}\). The other two principal stresses are basically horizontal, denoted the maximum horizontal principal stress and minimum horizontal principal stress, and are represented by symbols \(\sigma_{H}\) and \(\sigma_{h}\), respectively. The in situ stress value of each particle in the formation is characterized by the magnitude and direction of the vertical stress, maximum horizontal principal stress, and minimum horizontal principal stress. Among them, the minimum horizontal principal stress (\(\sigma_{h}\)) is the minimum pressure at which the reservoir rock is deformed and fractured along the plane direction under the action of an external force and reflects the difficulty of rock fracturing. The following formula is used to calculate:

$$\sigma_{\eta } = \frac{1.5\nu }{{1 - \nu }}p_{{\text{v}}} + \frac{1.5\nu h}{{1 + \nu }} \times 10^{ - 3} + \frac{0.0045E\Delta T}{{1 - \nu }} \times 10^{ - 4}$$
(9)

Among them:

$$p_{{\text{v}}} = \rho_{{\text{b}}} gh$$
$$\Delta T = 0.03h + 273.5$$

In the formula, \(\sigma_{h}\) is the minimum horizontal principal stress, MPa; \(\nu\) is the static Poisson’s ratio, dimensionless; pv is the vertical stress, MPa; \(\rho_{{\text{b}}}\) is the rock bulk density, g/cm3; h is the depth of the oil layer, m; E is the static Young’s modulus, MPa; and ΔT is the oil layer temperature, K. The calculation of static Poisson's ratio and static Young's modulus refers to the calculation method of formula (2) for the brittleness index.

According to the statistics of the relevant parameters of the oil layer in which different samples are located, the minimum horizontal principal stress is calculated by substituting the formula (Table 4).

Table 4 Minimum horizontal principal stress calculation table
Full size table

Determination of the weight of a single evaluation parameter

The gray relational analytical method is a method to analyse the degree of correlation of various factors in the system. It can process the data of various factors to be analyzed and studied with incomplete information. Then, their relevance among random factor sequences is determined, and the weight of a single evaluation parameter is obtained (Zhao et al. 2018). In this method, the correlation between the initial production and sweetness evaluation parameters is analyzed; that is, the correlation between the initial production and the six parameters of oil saturation, longitudinal structural coefficient of the oil layer, average pore throat radius, gas-oil ratio, brittleness index, and minimum horizontal principal stress, are analyzed. In particular, the representativeness of production has a greater impact on the calculated results of parameter weights. Generally, the number of wells not only must be large but also needs to be evenly distributed on the plane, and the initial production size should also be reasonably distributed. The correlation coefficient between the initial production and evaluation parameters is calculated according to the formula \(\xi\) (Tables 5 and 6):

$$\mathop \xi \nolimits_{i} \left( k \right) = \frac{{\min \mathop {\min }\limits_{k} \mathop \Delta \nolimits_{i} (k) + \rho \max \mathop {\max }\limits_{k} \mathop \Delta \nolimits_{i} (k)}}{{\mathop \Delta \nolimits_{i} (k) + \rho \max \mathop {\max }\limits_{k} \mathop \Delta \nolimits_{i} (k)}}$$
(10)
Table 5 Normalized evaluation parameters
Full size table
Table 6 Absolute values of normalized single well production after subtraction of normalized evaluation parameters
Full size table

Among them:

$$\Delta_{i} (k) = \left| {\Delta A_{i} (k) - \Delta A_{0} \left( k \right)} \right|$$
$$\Delta A_{0} (k) = \frac{{A_{0} (k) - A_{0} \left( k \right)_{\min } }}{{A_{0} \left( k \right)_{\max } - A_{0} \left( k \right)_{\min } }}$$
$$\Delta A_{i} (k) = \frac{{A_{i} (k) - A_{i} \left( k \right)_{\min } }}{{A_{i} \left( k \right)_{\max } - A_{i} \left( k \right)_{\min } }}$$

In the formula, \(\xi_{i} (k)\) is the correlation degree of the i-th parameter of the k-th well, dimensionless; \(\Delta_{i} (k)\) is the difference between the normalized initial production and normalized evaluation parameter, dimensionless; \(\min \mathop {\min }\limits_{k} \mathop \Delta \nolimits_{i} (k)\) is the minimum value among the minimum values of the normalized initial production of all wells after subtracting the normalized evaluation parameters, dimensionless; \(\max \mathop {\max }\limits_{k} \mathop \Delta \nolimits_{i} (k)\) is the maximum value among the maximum values of the normalized initial production of all wells after subtracting the normalized evaluation parameters and is dimensionless; \(\Delta A_{0} (k)\) is the normalized initial production, dimensionless; \(\Delta A_{i} (k)\) is a normalized evaluation parameter, dimensionless; and \(A_{0} (k)\) is the initial production of the k-th well, t/d. \(A_{i} (k)\) is the i-th evaluation parameter of the k-th well, and the unit is the corresponding unit of each parameter (oil saturation (%), longitudinal structural coefficient of the oil layer (dimensionless), average pore throat radius (um), gas-oil ratio (t)/m3), brittleness index (%), and minimum horizontal principal stress (MPa)). \(\rho\) is the resolution coefficient, generally taken as (0, 1) or taken as 0.5.

The correlation coefficient of each evaluation parameter corresponding to each well is calculated, and then the average method to calculate the correlation degree between each parameter and production is used:

$$\mathop \gamma \nolimits_{i} = \frac{1}{n}\sum\limits_{k = 1}^{m} {\mathop \xi \nolimits_{i} (k)}$$
(11)

In the formula, \(\gamma_{i}\) is the correlation degree of the i-th parameter, dimensionless; n is the number of evaluation parameters; m is the number of evaluation wells; and \(\xi_{i} (k)\) is the correlation degree of the i-th parameter of the k-th well, dimensionless.

After obtaining the degree of association, the weight coefficient is obtained by normalization (Table 7):

$$a_{i} = \frac{{\mathop \gamma \nolimits_{i} }}{{\sum\limits_{1}^{n} {\gamma_{i} } }} \times 100$$
(12)
Table 7 Evaluation parameters and weight coefficient of production
Full size table

In the formula, ai is the weight coefficient of each evaluation parameter, decimal; \(\gamma_{i}\) is the correlation degree of the i-th parameter, dimensionless; and n is the number of evaluation parameters, and the number of evaluation parameters in this method is 6.

Establishment of classification evaluation standards

Construction of the evaluation index

To remove the influence of the evaluation parameter unit on the evaluation index, the evaluation index is defined as the sum of the normalized evaluation parameters and the corresponding weight coefficients:

$${\text{SSEV}} = \sum\limits_{1}^{n} {(\Delta A_{i} \times a_{i} )}$$
(13)

In the formula, SSEV is the evaluation index, dimensionless. \(\Delta A_{i}\) is the i-th normalized evaluation parameter, dimensionless; ai is the weight coefficient of each evaluation parameter, decimal; and n is the number of evaluation parameters, and the number of evaluation parameters in this method is 6.

Establishing classification standards

According to the calculated evaluation index of each well, the correlation formula between the evaluation index of the Chang 7 oil group in the Ordos Basin and single well production is established:

$${\text{SP}} = 0.0441 \times e^{{5.3259\, \times \,{\text{SSEV}}}}$$
(14)

In the formula, SP is the single well production, and the unit is t/d; and SSEV is an evaluation index, with a value between 0 and 1, dimensionless.

According to the calculated evaluation indexes of different sample wells, the Chang 7 reservoir in the Ordos Basin is divided into three types (Fig. 1). On the basis of establishing the relationship curve between the evaluation index of the evaluation area and production index, the two end points A and B of the curve are tangent lines L1 and L2 of the index curve, respectively. The two tangent lines intersect at point C and cross point C to make a vertical line connecting end points A and B. The vertical line intersects the exponential curve at point D. The tangent line L3 of the exponential curve parallel to the line segments A and B is made through point D, and the vertical line of the abscissa is made through the intersection of L1 and L3 and L2 and L3. In this way, the Chang 7 oil group in the Ordos Basin is divided into 3 types, and the intersection point is the boundary value of the classification. The evaluation index SSEV ≧ 0.65 is type I, the evaluation index 0.4 ≦ SSEV < 0.65 is type II, and the evaluation index SSEV < 0.4 is type III.

Fig. 1
figure 1

Relationship between sweetness evaluation index and single well production

Full size image

Determination of the distribution range of individual indicators

According to the classification results of the Chang 7 reservoir group evaluation index in the Ordos Basin, the statistics of the individual parameters of different sample wells (oil saturation, average pore throat radius, longitudinal structural coefficient of the oil layer, gas-oil ratio, brittleness index, and minimum horizontal principal stress) are calculated for the distribution area. Considering that the test values of total hydrocarbons in different sample wells are low, the distribution range of total hydrocarbons is mainly determined by the classification limit of oil saturation (Table 8).

Table 8 Classification and evaluation indexes of Chang 7 reservoir group in Ordos Basin
Full size table

Conclusions

Using the geological-engineering integrated evaluation idea, an evaluation parameter system for the sweetness classification of tight oil is established, and the value method is given. Evaluation parameters include oil saturation, longitudinal structural coefficient of the oil layer, average pore throat radius, gas-oil ratio, brittleness index, and minimum horizontal principal stress. Based on the relationships between each parameter and the initial production of the directional well, the gray correlation method is used to quantify the weight of the contribution of the evaluation parameter to production. Based on this and using the curve slope difference method, a sweetness evaluation and classification method suitable for the Chang 7 oil group in the Ordos Basin is constructed, which solves the difficult problem of quality difference classification of the Chang 7 oil group. The Chang 7 oil group in the Ordos Basin is divided into 3 types, and the intersection point is the boundary value of the classification. The evaluation index SSEV≧0.65 is type I, the evaluation index 0.4 ≦ SSEV < 0.65 is type II, and the evaluation index SSEV < 0.4 is type III.