Introduction

The prediction of wellbore temperature and pressure field has always been a major problem of common concern to scientists (Mirabbasi et al. 2020), because it is related to the accurate construction of oil production technology (Li et al. 2020; Jung et al. 2020), the safety of pipe string (Guo et al. 2021; Li et al. 2021; Wang et al. 2019a), the normal use of various downhole tools (Wang Sifan, Zhang Ankang, Hu Dongfeng 2021), the reliability of production process (Wang et al. 2019b), and the wax and scale prevention of oil and gas wells affected by temperature and pressure (Wei et al. 2017; Dalong et al. 2021; Yang et al. 2021; Wang 2019). Nowadays, in the daily production process of gas wells, the phase change of natural gas in the wellbore is becoming more and more common (Gholamzadeh et al. 2020; Wei et al. 2019). As we all know, in the process of oil well production, the high-temperature formation fluid flows to the wellhead through the tubing under the action of formation pressure. Because the temperature of the formation fluid in the tubing is higher than the ambient temperature around the tubing, the formation fluid will transfer heat to the surrounding during the flow process (Yi, et al. 2021). However, gas wells are slightly different from oil wells. Due to the high bottom hole pressure, natural gas shows liquid flow at the bottom of the well. However, with the gradual decrease in wellbore pressure and temperature, the temperature and pressure of natural gas change, that is, the phase state of natural gas changes greatly. The phase change position, water content, and real-time wellbore temperature and pressure field of natural gas are closely related to the rational use of downhole tools (Shengji 2019), and then affect the production of gas wells (Qiang et al. 2021). In order to solve this engineering problem, many scholars have proposed new calculation and prediction methods to calculate and obtain the data of temperature field and pressure field of gas wells under various conditions.

By summarizing the current existing technology, the similar methods are:

Based on the simulation results of single-phase flow in horizontal wellbore, Ting Dong et al. (Xu et al. 2018) proposed a two-phase flow model (GSDRIVED model) in the form of homogeneous and drift flow model suitable for open hole completion and perforation completion. However, the model only puts forward the two-phase flow model, and does not consider the calculation of the temperature and pressure field of the key wellbore parameters.

Zhang et al. (2021) studied the separation efficiency of the new filter separator by using indoor simulation experiments. Based on the separation efficiency, wellbore flow theory and the first law of thermodynamics, fully considered the dynamic mass flow at the separator and the influence of wellbore temperature and pressure on thermophysical parameters, established the wellbore temperature and pressure coupling model based on dynamic mass flow, Finally, the model is discretized and solved by finite difference method and cyclic iteration method. However, the model is only applicable to the study of the separation efficiency of the new filter separator, and the calculation of the temperature and pressure field of the key parameters in the wellbore of high water-bearing gas wells is not discussed.

Mostafa M. Abdelhafiz et al. (Abdelhafiz et al. 2021) proposed a model for predicting the temperature distribution of vertical wellbore system under circulation and shut-in conditions. The model can simulate the transient temperature disturbance of drilling fluid, drill string, casing string, cement behind casing, and surrounding rock formation. However, the coupling effect of temperature and pressure is not considered in the model.

Wei Na et al. (Wei et al. 2019) studied the dynamic decomposition law of hydrate in the above process by establishing the multiphase wellbore flow mathematical model of wellbore temperature field, pressure field, hydrate phase equilibrium, and hydrate dynamic decomposition in multiphase riser flow and proposed and verified the numerical calculation method of wellbore multiphase flow coupled hydrate dynamic decomposition. However, for hydrate decomposition, the model does not consider the coupling calculation of temperature and pressure in the throttling process of high water-bearing gas wells.

Based on the experimental study of heat transfer of single-phase flow and gas–liquid two-phase flow in the wellbore, Zhaokai Hou et al. (Hou et al. 2019) proposed a series of new correlations for calculating the convective heat transfer coefficients of various flows (including single flow, bubble flow, intermittent flow, and annular flow), analyzed the wellbore temperature by using the improved heat transfer model, and obtained the drilling fluid displacement, inlet temperature The influence of geothermal gradient and formation gas invasion velocity on wellbore temperature. But, the coupling effect of temperature and pressure is not considered in the model.

However, the above methods do not mention the prediction of wellbore temperature and pressure of high water-cut natural gas under high temperature and high pressure. Therefore, taking the gas wells in the Daning-Jixian block as the research object, this paper not only considers the wellbore heat transfer, but also considers the influence of formation temperature and wellbore pressure on the phase state of natural gas, establishes the wellbore pressure coupling model of water-bearing gas wells, and discusses the tubing diameter, gas production, gas–water ratio, and wellbore temperature field of high water-bearing gas wells pressure field.

Firstly, this study analyzes the shortcomings of Ramey model and Hassan & Kabir model, and gives an appropriate gas–liquid two-phase flow wellbore temperature and pressure field coupling calculation model. Secondly, the model is substituted into the field actual case calculation. Then, the error of the model is analyzed. Finally, the sensitivity of the model is analyzed.

Model analysis

The Ramey method is proposed to solve the description of the heat transfer process in the radial direction of the wellbore by the injected fluid, assuming that the heat transfer in the wellbore is a steady-state process, and the heat transfer to the formation is a non-steady-state process. The specific research process starts from the known rate and temperature of injected fluid and determines the functional relationship between injected fluid temperature and wellbore depth and injection time by establishing a suitable calculation model.

If the injected fluid is liquid, the relationship between injection temperature and wellbore depth, and injection time is expressed as Eq. (1):

$$T_{1} (z,t) = aZ + b - aA + (T_{0} + aA - b)e^{ - Z/A} .$$
(1)

If the injected fluid is gaseous, it is expressed as Eq. (2):

$$T_{1} \left( {z,t} \right) = aZ + b - A\left( {a + \frac{1}{778c}} \right) + \left[ {T_{0} - b + A(a + \frac{1}{778c})} \right]e^{ - Z/A}$$
(2)
$$A = \frac{{Wc\left[ {k + r_{1} Uf(t)} \right]}}{{2\pi r_{1} Uk}}.$$

Formulas (1)–(2) are established on the premise that the thermodynamic properties of formation and wellbore fluid do not change with temperature, heat will be transferred radially in the formation, and heat transfer in the wellbore is faster than that in the formation. Therefore, it can be expressed by a steady-state solution. References about the specific solution of the Ramey model (Ramey 1962). The value of the Ramey model is to simplify the model into the radial heat conduction problem of the infinite cylinder by introducing a dimensionless time function. Such use of reservoir engineering transient fluid flow can be completely solved. But Ramey model cannot describe the wellbore temperature field well because of too many assumptions.

Hassan & Kabir (Bo et al. 2014) considered that the wellbore flow is mostly gas–liquid two-phase flow, based on the drift model, the gas–liquid two-phase pipe flow theory was used to describe the fluid flow in the wellbore. Through different flow forms, the pressure gradient of gas–liquid two-phase pipe flow is expressed as the sum of gravity, friction, and acceleration, which can be expressed as:

$$\frac{dp}{{dz}} = - \rho_{m} g\sin \theta - f_{m} \times \frac{{\rho_{m} v_{m}^{2} }}{2D} - \rho_{m} v_{m} \frac{{dv_{m} }}{dz}.$$
(3)

Deformed form (3), taking into account ground production, may be expressed as form (4):

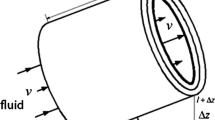
$$10^{6} \frac{\Delta \rho }{{\Delta H}} = \rho_{m} g + \frac{{f_{m} q_{L}^{2} M_{t}^{2} }}{{9.21 \times 10^{9} \rho_{m} d^{5} }} + \frac{{\rho_{m} \left( {\frac{{u_{m}^{2} }}{2}} \right)}}{\Delta H}.$$
(4)

Hassan & Kabir model established a good relationship between production and wellbore pressure drop. Through the flow data between gas–liquid sub-items, combined with the friction of each phase in the wellbore, the gas–liquid two-phase flow was fully expressed by dividing the wellbore infinitesimal. However, the model essentially only describes the wellbore pressure and does not couple the wellbore temperature field. In fact, the pressure and temperature of the production well are interdependent. Considering the defects of the Ramey model and Hassan & Kabir model, the wellbore temperature–pressure coupling model of a water-bearing gas well is established by combining wellbore heat transfer mechanism and gas–liquid two-phase homogeneous flow equation (Fig. 1).

Fig. 1
figure 1

Problem research flowchart

Full size image

The fluid flow in the wellbore is regarded as one-dimensional flow, that is, the flow parameters and physical parameters of gas and liquid phases in the pipeline at any cross section are uniforms, which is the average value of the cross section. The homogeneous flow model in the two-phase flow research method is used for analysis.

(1) Continuity equation.

A one-dimensional flow section is taken into study. Its diameter and the area of the flow section are as shown in Fig. 2. The flow model is established along the flow direction. The continuity equation can be expressed as:

$$\rho_{g} u_{g} a + \rho_{l} u_{l} \left( {1 - a} \right) = \frac{Q}{A} = G$$
(5)
$$\rho_{m} = a\rho_{g} + \left( {1 - a} \right)\rho_{l} .$$
(6)
Fig. 2
figure 2

Diagram of one-dimensional gas–liquid two-phase flow

Full size image

In the homogeneous flow model, the slip velocity ratio, that is, the gas–liquid two-phase has no slip, can be obtained:

$$\rho_{m} = \beta \rho_{g} + \left( {1 - \beta } \right)\rho_{l} .$$
(7)

(2) Momentum equation.

Similar to the single-phase flow, the momentum equation of homogeneous flow can be written the form of three pressure drop gradients (Lining 2017), which can be expressed as:

$$- \frac{dp}{{dz}} = \left( {\frac{{dp_{g} }}{dz}} \right) + \left( {\frac{{dp_{f} }}{dz}} \right) + \left( {\frac{{dp_{a} }}{dz}} \right).$$
(8)

The pressure gradient generated by the gravity of homogeneous flow is:

$$\left( {\frac{{dp_{g} }}{dz}} \right) = \rho_{m} \sin \theta .$$
(9)

The friction gradient can be expressed as:

$$\left( {\frac{{dp_{f} }}{dz}} \right) = \frac{\tau \pi d}{A}$$
(10)
$$\left( {\frac{{dp_{f} }}{dz}} \right) = 2\rho_{m} g \cdot f\frac{1}{d}\frac{{v^{2} }}{g}$$
(11)

where the Vanning friction coefficient of two-phase flow (Chunqiu and Yingchuan 2001; Willhiteg 1967; Tragesser et al. 1967; Arnold 1990; Chiu and Thakur 1991; Hasan et al. 1996; Hagoort 2004; Zhao Jin and Xianliang 2015).

The acceleration pressure gradient can be expressed as:

$$\left( {\frac{{dp_{a} }}{dz}} \right) = G^{2} \frac{{dv_{m} }}{dz}$$
(12)
$$- \frac{dp}{{dz}} = \rho_{m} \sin \theta + 2\rho_{m} g \cdot f\frac{1}{d}\frac{{v^{2} }}{g} + G^{2} \frac{{dv_{m} }}{dz}.$$
(13)

(3) Energy equation.

In the homogeneous flow model, according to the principle of energy conservation, the energy conservation equation of infinitesimal is (Yongjian et al. 2019): flow work + internal energy + kinetic energy + potential energy = joining heat − system external work that can be expressed as:

$$d\left( {pv} \right) + dU + d\left( {\frac{1}{2}u^{2} } \right) + g\sin \theta dz = dq - dw$$
(14)
$$\begin{gathered} d\left[ {apu_{g} + \left( {1 - a} \right)pu_{l} } \right] + dq - pd\left[ {au_{g} + \left( {1 - a} \right)u_{l} } \right] \hfill \\ + d\left[ {\frac{1}{2}au_{g}^{2} + \frac{1}{2}\left( {1 - a} \right)u_{l}^{2} } \right] + \rho g\sin \theta dz = dq - dw. \hfill \\ \end{gathered}$$
(15)

Due to the gas–liquid two-phase flow in wellbore, the fluid does not work outside. Therefore:

$$\begin{gathered} d\left[ {apu_{g} + \left( {1 - a} \right)pu_{l} } \right] + dq - pd\left[ {au_{g} + \left( {1 - a} \right)u_{l} } \right] \hfill \\ + d\left[ {\frac{1}{2}au_{g}^{2} + \frac{1}{2}\left( {1 - a} \right)u_{l}^{2} } \right] + \rho g\sin \theta dz = dq. \hfill \\ \end{gathered}$$
(16)

By introducing specific enthalpy and taking the micro-element section with length of dz on the tubing, the energy conservation equation can be obtained as follows:

$$\frac{dh}{{dz}} = - \frac{{V_{m} dV_{m} }}{dz} - g\sin \theta - \frac{q}{Q}.$$
(17)

The specific enthalpy is the function of temperature and pressure, namely:

$$dh = \left[ {\frac{\partial h}{{\partial T}}} \right]_{p} dT + \left[ {\frac{\partial h}{{\partial p}}} \right]_{T} dp = C_{p} dT - C_{J} C_{p} dp.$$
(18)

The heat transferred radially from fluid in wellbore to the second contact surface (the contact surface between cement sheath and formation) can be approximately expressed as (Izgec et al. 2008):

$$Q_{1} = - 2\pi r_{to} U_{to} \left( {T_{f} - T_{s} } \right)dz.$$
(19)

The radial heat transfer from the second contact to the surrounding strata is:

$$Q_{2} = - \frac{{2\pi k_{e} \left( {T_{s} - T_{ei} } \right)}}{f\left( t \right)}dz.$$
(20)

The heat transferred from the wellbore to the second contact surface is equal to the heat transferred from the second contact surface to the surrounding strata. The outlet temperature for each paragraph is:

$$T_{fout} = e^{{\lambda \left( {z_{out} - z_{in} } \right)}} \left( {T_{fin} - \frac{g\sin \theta }{{\lambda C_{p} }} + \frac{\eta }{\lambda } - T_{ein} + \frac{{g_{l} }}{\lambda }} \right) + \frac{g\sin \theta }{{\lambda C_{p} }} - \frac{\eta }{\lambda } + T_{eout} - \frac{{g_{l} }}{\lambda }$$
(21)
$$\eta = C_{J} \frac{dp}{{dz}} - \frac{v}{{C_{p} }}\frac{dv}{{dz}},\lambda = \frac{{2\pi r_{to} U_{to} k_{e} }}{{C_{p} w\left( {k_{e} + f\left( t \right)r_{to} U_{to} } \right)}}.$$
(22)

The Joule Thomson coefficient can be expressed as (Wei 1999):

$$C_{J} = \frac{1}{{C_{p} }}\left[ {\left( {\frac{{W_{g} T}}{{Z_{g} \rho_{g} }}} \right)\left( {\frac{{\partial Z_{g} }}{\partial T}} \right)_{p} - \frac{{\left( {1 - W_{g} } \right)\left( {1 - \beta T} \right)}}{{\rho_{l} }}} \right]$$
(23)
$$\begin{gathered} \hfill \\ \beta = \left( \frac{1}{v} \right)\left( {\frac{\partial V}{{\partial T}}} \right)_{p} = \left( { - \frac{1}{\rho }} \right)\left( {\frac{\partial \rho }{{\partial T}}} \right)_{p} . \hfill \\ \end{gathered}$$

The above temperature and pressure model of gas–liquid two-phase flow in the wellbore are calculated, in which the temperature model contains temperature and pressure variables, and each physical property parameter is a function of temperature and pressure, which needs to be solved by an iterative method. The wellbore is divided into n sections. Assuming that the thermophysical parameters in each section are equal, the temperature and pressure parameters at the bottom of the well are set as boundary conditions, and the relevant physical parameters of the next section are calculated according to the temperature and pressure until the complete wellbore is calculated.

Field case calculation

Based on the established temperature–pressure coupling model of high water-cut gas wells, the above model is verified by combining it with the actual wellbore data. The relative errors of the Ramey model, Hassan & Kabir model, and temperature–pressure coupling model of high water-cut gas wells are compared with the measured data. The temperature and pressure distribution of wellbore temperature and pressure field with the change of tubing size, gas production, and the gas–water ratio is obtained.

Table 1 gives the wellbore structure parameters of Well Daji 14-1 and Well Daji 4-5 in the Daning-Jixian block.

Table 1 Well structure parameters of Daji 14-1 and Daji 4-5
Full size table

For the above Daji 14-1 well, the surface casing depth is 554.91 m, the gas casing depth is 2471.75 m, the surface casing depth of Daji 4-5 well is 554.64 m, and the gas casing depth is 2486.47. Since the overall GWR of the two wells is less than 2000, it cannot be treated as a single-phase gas well. The temperature–pressure coupling theoretical model of the water-bearing gas well is used, and the calculation results are shown in Fig. 2 by MATLAB programming.

As shown in Fig. 3, the established wellbore temperature–pressure coupling model of water-bearing gas wells has higher accuracy than Hassan & Kabir model and Ramey model and is closer to the field measured data. It can be seen from the figure that the Ramey model cannot make a correct judgment on the wellbore temperature and pressure field of high water-cut gas wells. Hassan & Kabir model is more accurate than the Ramey model because of the theoretical basis of the two-phase pipe flow model. However, when calculating wellbore temperature and pressure field, the pressure drop is calculated first, and the relationship between pressure change and temperature change is considered independently, which has a large deviation from the actual field. For Daji 14-1 well model temperature prediction is more accurate, pressure prediction error. There are two reasons for this phenomenon: (1) In the pressure calculation of the model, it is caused by the discontinuous formation pressure gradient. (2) The measured pressure data will also lead to deviation from the theoretical calculation value due to the actual measurement error. For Daji 4-5 well, wellbore pressure prediction is more accurate and temperature error is relatively large. This may be due to the fact that the model approximately considers the continuous variation of the geothermal gradient in the calculation of formation temperature. This theoretical model can be applied to engineering practice.

Fig. 3
figure 3

Temperature and pressure distribution of wellbore

Full size image

Model error analysis

Due to the different dimensions and well conditions between the four groups of data in Fig. 2, a unified error cannot be used for comparative analysis. The coefficient of variation is introduced to describe the deviation degree between each model and the field measured data. The coefficient of variation can be expressed as:

$$C_{v} = \frac{\sigma }{\mu }.$$
(24)

In the equation, \(C_{v}\)is the coefficient of variation, \(\sigma\) standard deviation, and \(\mu\) average.

The results obtained by coefficient of variation analysis on the four groups of data are shown in Table 2.

Table 2 Coefficients of variation of each model
Full size table

The discrete points of data in Table 2 are expressed in two-dimensional coordinates as shown in Fig. 4.

Fig. 4
figure 4

Comparison of variation coefficient of each model

Full size image

As shown in Fig. 4, the temperature–pressure coupling prediction model of high water-cut gas wells established in this paper has the smallest coefficient of variation in the four sets of data tests, indicating that the discrete degree of field measured data is the smallest and has the highest accuracy.

Sensitivity analysis

The actual wellbore temperature and pressure field in the field are often affected by multiple factors, such as gas production, gas–water ratio, and tubing size change. Based on the established single-phase gas well temperature and pressure field model and high water-cut gas well temperature and pressure model, the influencing factors of wellbore temperature and pressure field are analyzed. The variation of wellbore temperature and pressure with tubing sizes of 2 and a half inches, 3 and a half inches, and 4 inches was obtained by analysis. The change of wellbore temperature and pressure field when gas production is 30,000, 50,000, and 100,000 square. The change of wellbore temperature and pressure field at gas–water ratios of 2000, 1000, and 800. The results are shown in Figs. 5, 6, and 7.

Fig. 5
figure 5

Curve of temperature and pressure versus tubing diameter

Full size image
Fig. 6
figure 6

Curve of temperature pressure versus gas production

Full size image
Fig. 7
figure 7

Curve of temperature pressure versus gas–water ratio

Full size image

It can be obtained from Fig. 5 that for Daji 14-1 and Daji 4-5 gas wells, the influence of the inner diameters of 2.5 inches, 3 inches, 3.5 inches, and 4 inches of tubing on the wellbore temperature and pressure field is analyzed. The change of the inner diameter of tubing will cause the change of the wellbore temperature and pressure field. The results show that: (1) With the increase in tubing diameter, wellhead temperature will gradually decrease. This is due to the increase in the inner diameter of the tubing and the increase in the convective heat transfer area of the fluid in the tubing, which enhances the heat exchange process and leads to the decrease in wellhead temperature. (2) With the increase in tubing diameter, wellhead pressure will increase. This is because the increase in the inner diameter of the tubing will lead to an increase in the fluid in the unit cross-sectional area, resulting in an increase in the pressure in the wellbore.

It can be obtained from Fig. 6 that for Daji 14-1 and Daji 4-5 gas wells, the influence of gas production of 30,000, 50,000, and 100,000 square on wellbore temperature and pressure field is analyzed. The results show that: (1) With the increase in gas production, wellhead temperature will gradually increase. This is because the increase in gas production leads to the increase in fluid per unit cross-sectional area of tubing, and a large number of fluids cannot reach the convective heat transfer, resulting in an increase in wellbore temperature. (2) With the increase in gas production, the wellhead pressure will decrease. This is because, with the increase in gas production, the volume flow of the instantaneous discharged fluid will increase, resulting in the increase in gravity friction, thus increasing the pressure loss and reducing the pressure in the wellbore.

As shown in Fig. 7, for Daji 14-1 and Daji 4-5 gas wells, the effects of gas–water ratios of 2000, 1000, and 800 on wellbore temperature and pressure fields are analyzed. The results show that: (1) With the increase in gas–water ratio, wellhead temperature will gradually decrease. This is because the increase in the gas–water ratio leads to a large proportion of the gas phase. The specific heat capacity of water is higher than that of natural gas fluid, and the heat transfer ability is stronger. Therefore, the small proportion of water leads to the weakening of heat transfer ability, resulting in the gradual increase in wellbore temperature. (2) With the increase in gas–water ratio, the wellhead pressure will increase, which is the increase in the proportion of gas components. Due to the compressibility of gas, the pressure distribution in the wellbore is higher than that in the low gas–water ratio, resulting in the gradual increase in wellbore pressure distribution.

Summary and conclusions

The purpose of this study is to model and analyze the throttling production process of high water content gas wells, which is not suitable for other working conditions. The example calculation is carried out for several wells in a block, and the influence of natural environmental factors on the results is not excluded.

Based on the wellbore heat transfer mechanism, considering gas thermophysical parameters and Joule–Thomson coefficient, a wellbore pressure–temperature coupling prediction model for high water-cut gas wells is established. The variation coefficient method was used to explore the relationship between the prediction model and Hassan & Kabir model, Ramey model and field measured data, and the accuracy of the model was verified. The sensitivity analysis of wellbore temperature and pressure field was carried out. The relationship between tubing diameter, gas production, gas–water ratio, and wellbore temperature and pressure field of high water-cut gas wells was explored. The wellbore temperature–pressure coupling model of single-phase gas well and the temperature–pressure calculation model of high water-cut gas well are established, respectively, and the model is verified by Daji 14-1 and Daji 4-5 gas wells. The main conclusions are as follows:

(1) Compared with Hassan & Kabir model and Ramey model, the established wellbore temperature and pressure coupling model of water-bearing gas wells has higher accuracy. The minimum values of various coefficients of each model are 0.022, 0.037, and 0.042, respectively, indicating that the wellbore temperature and pressure coupling prediction model of high water-bearing gas wells is closer to the field measured data. Ramey model cannot make a correct judgment on wellbore temperature and pressure field of high water-cut gas wells. Hassan & Kabir model is more accurate than the Ramey model because of the theoretical basis of the two-phase pipe flow model. However, when calculating wellbore temperature and pressure field, the pressure drop is calculated first, and the relationship between pressure change and temperature change is considered independently, which has a large deviation from the actual field.

(2) The wellbore temperature and pressure change when the inner diameter of the tubing is 2 inches and half, 3 inches, 3 inches and half, and 4 inches are studied, respectively. It is found that with the increase in the inner diameter of the tubing, the wellhead temperature will gradually decrease. This is due to the increase in the inner diameter of the tubing and the increase in the convective heat transfer area of the fluid in the tubing, which enhances the heat exchange process and leads to the decrease in wellhead temperature. With the increase in tubing diameter, wellhead pressure will increase. This is because the increase in the inner diameter of the tubing will lead to an increase in the fluid in the unit cross-sectional area, resulting in an increase in the pressure in the wellbore.

(3) The change of wellbore temperature and pressure field when gas production is 30,000, 50,000, and 100,000 square is studied. It is obtained that the wellhead temperature will gradually increase with the increase in gas production. This is because the increase in gas production leads to the increase in fluid per unit cross-sectional area of tubing, and a large number of fluids cannot reach the convective heat transfer, resulting in an increase in wellbore temperature. With the increase in gas production, the wellhead pressure will decrease. This is because, with the increase in gas production, the volume flow of the instantaneous discharged fluid will increase, resulting in the increase in gravity friction, thus increasing the pressure loss and reducing the pressure in the wellbore.

(4) The change of wellbore temperature and pressure field at gas–water ratios of 2000, 1000, and 800 is studied. It is obtained that the wellhead temperature will gradually decrease with the increase in the gas–water ratio. This is because the increase in the gas–water ratio leads to a large proportion of the gas phase. The specific heat capacity of water is higher than that of natural gas fluid, and the heat transfer ability is stronger. Therefore, the small proportion of water leads to the weakening of heat transfer ability, resulting in the gradual increase in wellbore temperature. With the increase in gas–water ratio, the wellhead pressure will increase, which is the proportion of gas components increases. Due to the compressibility of gas, the pressure distribution in the wellbore is higher than that in the low gas–water ratio, resulting in the gradual increase in wellbore pressure distribution.