Abstract
One of the most important oil and gas drilling studies is wellbore stability analysis. The purpose of this research is to investigate wellbore stability from a different perspective. To begin, vertical stress and pore pressure were calculated. The lowest and maximum horizontal stress were calculated using poroelastic equations. The strike-slip to normal fault regime was shown by calculated in situ stress values. The 1-D geomechanical model was utilized to investigate the failure mechanisms and safe mud window estimation using the Mohr–Coulomb failure criterion. Using density and sonic (compressional and shear slowness) logs, the acoustic impedance (AI) and reflection coefficient (RC) logs were determined subsequently. The combination of layers with different AI indicates positive and negative values for the RC, zones prone to shear failure or breakout, and the mud weight in these zones should be increased, according to the interpretation of the AI and RC readings and the results of the geomechanical model. Furthermore, the zones with almost constant values of AI log and values close to zero for RC log are stable as homogeneously lithologically, but have a lower tensile failure threshold than the intervals that are sensitive to shear failure, and if the mud weight increases, these zones are susceptible to tensile failure or breakdown. Increased porosity values, which directly correspond with the shear failure threshold and inversely with the tensile failure threshold, cause AI values to decrease in homogenous zones, but have no effect on the behavior of the RC log. This approach can determine the potential zones to kick, loss, shear failure, and tensile failure in a short time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Wellbore stability analysis is an essential part of a comprehensive field study designed to minimize the risk of drilling operations and thus reduce the costs associated with these operations in the oil and gas industry. Wellbore stability can be characterized as preventing mechanical failures and falls due to mechanical stress in the well, chemical reactions between the drilling fluid and the well, well drilling path, and drilling parameters (Mondal and Chatterjee 2019). Before drilling, the stress on the ground is less than the strength of the rocks and thus the balance of the ground is retained. But both during and after the drilling, part of the rock column is drilled and moved out of the well, and the drilling mud replaces that and puts pressure on the wellbore wall, thus spreading stress around the wellbore, and the balance of stress in the ground is disrupted and the stress generated by the drilling is created. To maintain wellbore stability and regulate these stresses, the well must be drilled with the appropriate mud weight. (Darvishpour et al. 2019) Failure to pay attention to this issue causes wellbore instability and problems such as collapse, kick, wash-out or tighten, increasing drilling costs, stopping production, and eventually might indeed cause well loss (Das and Chatterjee 2017). Soft and plastic formations that are compressed into the wellbore, brittle rocks that fall into the well under stress and cause the drill bit to get stuck, or when the drill string is taken out of the wellbore was plugged, the most common problems with the instability of the wellbore are these. Decreasing the mud weight, salt content, viscosity and turbulent flow of the mud optimum the cost and improves the stability conditions. The major reasons for the mechanical instability of the wellbore are tensile failure and shear failure. There is also a minimum and maximum value for the drilling fluid pressure or weight of the drilling mud, which is estimated by the failure criterion (Gholami et al. 2014). The pressure of the drilling mud will cause a tensile failure in the wellbore and drilling mud will be lost into the formation if the mud weight is applied higher than the safe mud window. Shear failure or breakout will occur while this weight is applied lower than the safe mud window (Le and Rasouli 2012; Zhang 2013; Zoback et al. 2003). Consequently, one of the most critical parameters for maintaining wellbore stability is the drilling mud weight. In addition to the drilling mud weight parameter, other parameters such as the type of drilling mud and its chemical properties, well trajectory are also controllable parameters for wellbore stability. In comparison, the mechanical properties of the rocks, the initial stress of the region, and the pore pressure are among the uncontrollable parameters of the wellbore stability analysis. But one of the most effective operational ways to manage wellbore stability problems is to run the casing and the liner. However, sometimes the casing or liner installation in the well has been limited (Mohiuddin et al. 2007). Geomechanical modeling, wellbore stability analysis, and associated parameters have been examined in many research in recent years. Radwan et al. investigated pore pressure and fracture gradients using a variety of data and methods (Radwan et al. 2019, 2020, 2021; Radwan). They also carried out reservoir geomechanical modeling in order to analyze in situ stress and its relationship with reservoir properties such as depletion, production, and wellbore stability (Radwan and Sen 2021a, b; Radwan et al. , 2021). To improve under-balanced drilling, Abdelghany et al. applied the depth-of-damage method in geomechanical modeling (Abdelghany et al. 2021). Kassem et al. (2021) calculated the geomechanical parameters to investigate the effect of depletion and fluid injection in a sandstone reservoir (Kassem et al. 2021). Shahbazi et al. (2020) investigated the impact of reduced production rates on wellbore stresses by constructing a 2D geomechanical model using log data and drilling information in two Iranian oil fields. In a case study in Cunning Basin, Australia, Gholami et al. (2017) investigated wellbore stability by estimating geomechanical parameters and various stress states in wells drilled in heterogeneous formations. Han et al. (2019) established an advanced study of wellbore stability in naturally fracture rocks by providing three key steps for the measurement of elastic parameters, time-dependent analysis of poroelastic relations, and time-dependent analysis of fractured, porous, and double-permeable rocks of poroelastic relations, in the wellbore stability analysis. Khatibi et al. (2018) assessed the Single-Parameter Parabolic failure criterion using uniaxial compressive strength (UCS) from triaxial tests and from a geomechanical model in one of the Persian Gulf fields in Iran (Fig. 1).
The relationships between mud weight and wellbore stability (Bagdeli et al. 2019)
The integrity of the wellbore can be controlled by the weight of the mud and incidents such as tightness and wellbore failure or drilling mud loss can be avoided. Elastic parameters, rock strength characteristics, pore pressure, and knowledge of the state of stress in the well are included in the data used to estimate the safe mud window (Das and Chatterjee 2017; Mohiuddin et al. 2007).
Seismic reflectivity, which is connected to boundaries between zones of differing mechanical properties, is easier to comprehend than rock property attributes. The compressional (P-wave) acoustic impedance, as well as its S-wave equivalents and associated features, provides the fundamental explanation for generating such attributes (Morozov and Ma 2009). Acoustic impedance estimation is one of the main objectives of seismic data processing in seismic exploration. The accuracy of this parameter's reconstruction is particularly useful in obtaining subsurface information about formation properties and is particularly important in the interpretation of seismic data and reservoir characteristics (Guo and Wang 2019; Li et al. 2018; Mandal and Ghosh 2020; Wang and Wang 2017). The acoustic impedance of seismic data is commonly used as an important predictor for expressing rock characteristics and facilitating stratigraphic interpretation in geophysical studies (Li et al. 2018; Peng et al. 2008). Acoustic impedance is a rock attribute that can be obtained in two methods. One is the inversion method, which uses acoustic impedance obtained from seismic data, and the other is forward modeling using well logging data. In fact, seismic data is the inversion method, and it directly involves density and velocity, both of which may be measured directly by well logging (Latimer et al. 2000). The reflection coefficient is used to construct a mathematical model between acoustic impedance and seismic data to obtain acoustic impedance (Baziw and Ulrych 2006). In geophysical research, the reflection coefficient can be used as a function of angle, azimuth, frequency, and layer thickness. In the wellbore, however, sonic and density logs are employed to calculate these two parameters (AI and RC). Finally, these two parameters can also be used to match formation data and seismic data for comprehensive field studies. For different properties of reservoir rocks, several researchers have utilized acoustic impedance and reflection coefficient. Li et al. examined the poroelastic characteristics of gas reservoirs using a low-frequency seismic shadow approach that utilizes compressional reflection coefficient (Li and Rao 2020). Ekone et al. modeled the porosity using acoustic impedance and log data from the EK field in the Niger Delta (NO et al.). Xu et al. has used the frequency-dependent seismic reflex coefficient for the Discrimination of Gas Reservoirs (Xu et al. 2011). Banik et al. estimated pore pressure in the Gulf of Mexico employing acoustic impedance based on seismic data (Bjørlykke et al. 2015). Morozov and Jinfeng used well log calibration to improve the generation of acoustic impedance from seismic data (Morozov and Ma 2009). The two parameters of AI and RC are directly related to the mechanical properties of rocks in subsurface formations. Mechanical properties of the wellbore can be understood when these two parameters are measured in the well from log data. The major purpose of this research is to look into how AI and RC logs obtained from forward modeling behave when analyzing the condition of a wellbore from the aspect of wellbore stability analysis. First, geomechanical modeling will be used to evaluate the wellbore's stability and the safe mud window, and then the geomechanical model will be validated using the AI and RC parameters.
Geological setting
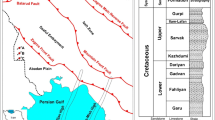
The oil field under investigation is one of Iran's most major oil fields. This field was discovered in 1999 and has estimated recoverable resources of 5.2 billion barrels and oil-in-place reserves of 32.2 billion barrels. This reservoir under investigation is Iran's second largest carbonate reservoir. This Middle Cretaceous (Albian–Thoronian) reservoir is one of the carbonate units of the Dezful embayment (Fig. 2) in the Zagros Basin, with an average thickness of 640 m.
The location of Dezful embayment in Zagros Basin of Iran (Masoudi et al. 2012)
Petrophysical properties
Petrophysical parameters such as effective and total porosity, water saturation–oil saturation, shale volume, and volume of minerals in this reservoir were calculated using probabilistic analysis. But first, the mineralogy composition was determined. Two litho-crossplots based on neutron and sonic logs vs density log are shown in Fig. 3. Figure 3 shows the most relevant lithology/porosity crossplot (a). The neutron versus density crossplot can be used to assess lithology composition and total porosity. Three lithological lines (sandstone, limestone, and dolomite) are depicted in this crossplot, with the placement of pointes and distance from matrix lines indicating mineralogy. On this plot, evaporate minerals, shale, and the gas impact can be seen. In this crossplot, total porosity will be evaluated using parallel lines on matrix lines. The same may be said for the density versus sonic crossplot displayed in Fig. 3. (b). The lithology composition of the examined reservoir is composed of limestone (calcite) with a few shale, as shown in Fig. 3a, b. In this carbonate reservoir limestone, the greatest total porosity in this reservoir is 25%.
Have been used Gamma-Ray (CGR), Thermal Neutron (TNPH), Compressional slowness (DTCO), Photoelectric absorption (PEF) and Resistivity logs (Rt and Rxo) in petrophysical model. After precomputations and environmental modifications, these logs were employed in the petrophysics model. The petrophysical evaluation results (Fig. 4) suggest a carbonate reservoir with limited shale volume (less than 10%) and a porosity average of 10%. The initial intervals of this formation contain a significant amount of oil. Figure 4 shows the volume of oil and water in the first column, and the volume of minerals in the second column, both from the right side. The conventional well logs that were employed in the petrophysical model were displayed in the other column of this figure.
Introducing the workflow
Conventional well logs, DSI log, FMI log, petrophysical evaluation results (mineral and porosity), and pore pressure points from MDT tools are the available data in this analysis. First, overburden stress was calculated using log data and experimental equations, and then the pore pressure was calculated by calibrating the MDT pore pressure points. After that, the rock elastic and strength parameters were computed. Next, minimum and maximum horizontal stress values were measured using poroelastic equations and then their orientations were observed by breakouts in the FMI image log. The results obtained from the geomechanical model were used to evaluate wellbore stability and determine the safe mud window. Next step, density and sonic logs (compressional and shear slowness) were used to calculate acoustic impedance and reflection coefficient logs as well as evaluate their behavior to wellbore stability analysis and compare with geomechanical model results. The research workflow is shown in Fig. 5.
Geomechanical modeling
Vertical stress and pore pressure
The pressure exerted by combining the vertical column pressure of various rock layers and the fluids inside themselves at a certain depth is overburden stress, commonly called vertical stress (Almalikee and Al-Najim 2018). Overburden pressure at each point in the subsurface due to the weight of upper layers and the role of different factors, such as rock type, porosity type, rock density, and the density of fluid filling the pores, diagenetic impact, tectonic factors, etc. This pressure includes lithostatic and hydrostatic pressures. Lithostatic pressure is the weight of rock column and hydrostatic pressure is the weight of fluid column filling the pore spaces. These pressures are a function of the specific gravity of the rocks and fluids within the pores and increase in proportion to the depth. The sum of these two pressures refers to overburden stress. The vertical stress (SV) can be easily determined from Eq. 1 if the upper layers have homogeneous properties in direct vertical depth (z):
However, the vertical stress (SV) at a specific depth (D) is determined from the following equation if the upper layers do not have homogeneous properties at the desired depth and have different lithological and petrophysical properties that ultimately have different densities:
where SV is the vertical stress in Pascal (N/m2), g is the gravity constant (9.8 g/s2), ρb is the total density (gm/cm3) and dz is the sum of the depth of pressure obtained can be converted to psi, provided that 1 psi = 6894.76 Pascal. But in most situations, to measure the vertical stress, the initial intervals of the drilled well do not have the density information. Consequently, a density can be calculated using a linear equation at the initial intervals from the ground to the target depth (Rana and Chandrashekhar 2015):
where ρEX is estimated density, ag is distance drilling floor to ground level, tvd is true vertical depth, ρML is surface density which about 2 (g/cm3), a and a0 are the calibration parameters in this equation. The hydrostatic pressure is also determined using the following equation, which is pressure at the depth of fluid column (Bjørlykke et al. 2015):
where ρf is the fluid density (gm/cm3). As a consequence, with increasing depth, the pressure gradient increases. For the analyzed interval, the amount of overburden stress was measured and the vertical stress gradient is in the range between 23 and 27 kPa/m and generally around 25.5 kPa/m (1.13 psi/ft) according to the experiences obtained from the direction determination project in North Dezful.
One of the vertical stress parameter applications is to use it to estimate the pore pressure. There are two ways to measure pore pressure. The first technique is direct pore pressure measurement using special logging tools such as MDT, RFT, etc. The second approach utilizes the indirect measurement of pore pressure from well log data such as density, resistivity, and acoustic. But experimental equations that use well logs can be used in non-reservoir periods, such as Eaton's equation (Eaton 1975). MDT tools information has been made available in this analysis at reservoir intervals. The pore pressure gradient obtained from MDT pore pressure points in this reservoir.
Rock elastic parameters
Rock mechanical parameters can be divided into two categories: elastic and strength parameters (Han et al. 2019). These Parameters such as Young's modulus, bulk module, shear modulus, and Poisson's ratio express the behavior and sensitivity of rock to variability or failure under stress which can be calculated both statically and dynamically. Using laboratory tests (uniaxial or triaxial) and the resulting stress–strain data, static elastic parameters are computed. As a conventional laboratory procedure, these tests are conducted on drilling core in plug scale to calculate the rock elastic parameters but there are disadvantages such as absence of a drilling core at all intervals, time limits, costs, etc. (Kong et al. 2019). Using well logs, is a faster and less expensive method to calculating of rock elastic parameters dynamically. Among the described elastic parameters, Young's modulus and Poisson's ratio are two key parameters in geomechanical modeling. Density log with compressional and shear velocity logs are used according to the following equations to measure dynamic Young modulus (Edyn) and dynamic Poisson ratio (νdyn):
where Edyn is dynamic Young's modulus, νdyn is Dynamic Poisson's ratios, ρ is density, Vp and Vs are compressional and shear velocity, respectively. As a result, using Eqs. 5 and 6, were calculated dynamic Young's modulus and dynamic Poisson's ratio. Calculated dynamic parameters for simulation of well condition are converted into static values. Conversion of dynamic data to static is accomplished by calibrating the results of laboratory tests (static values) for different rocks. In this research, were used Eqs. 7 and 8 to quantify the static Young's modulus and static Poisson's ratios according to prior studies and laboratory test in the studied field:
It is also possible to determine the bulk (K) and shear (G) modulus from the Young modulus and the Poisson ratio:
Rock strength parameters
The rock strength parameters are the Uniaxial Compressive Strength and Tensile Strength. In geomechanical studies, the UCS parameter is determined based on equations and correlations made using studies on various rock types in different fields when is not available laboratory data of rock strength. Then, the relationship between UCS and various physical properties of rocks was investigated by well logs in these studies (Amani and Shahbazi 2013). In this analysis, Eq. 11 has been used to measure the UCS parameter obtained from laboratory results in the studied field:
Tensile strength is typically measured from 1/8 to 1/12 of the uniaxial compressive strength (Zoback 2010). Here, Tensile strength is known to be 1/10 of uniaxial compressive strength (Eq. 12). Figure 6 illustrates the elastic parameters, vertical stress, pore pressure, mud weight, and well logs together with the results of the petrophysical evaluation.
From right side: first column shows pore pressure points from MDT (Pp2), pore pressure log calculated from MDT point (PPressure_Final), vertical stress (Sv), mud weight pressure (PMw). Second column shows dynamic bulk modulus (KMDyn) and dynamic shear modulus (GMDyn). Third column shows uniaxial compressive strength (UCS) and tensile strength (TENS_ST). Fourth column shows static Young's modulus (YMSta) and static Poisson's ratios (POIS_STATIC). Fifth column shows compressional slowness (DTCO) and shear slowness (DTSM). Sixth Column shows density log (RHOB). Seventh column shows lithology and porosity from petrophysical evaluation. Eighth Column shows gamma ray logs (CGR: thorium and potassium, GR: thorium, potassium and uranium). Ninth column shows bit size (BS) and caliper (C1 and C2). The last column is depth
Maximum and minimum horizontal stresses
The minimum and maximum horizontal stresses are two of the three major stresses required for each geomechanical study (in particular, wellbore stability analysis, sand production, and hydraulic fracture) (Shmin and Shmax). Estimation of horizontal stresses is one of the main steps in geomechanical modeling and contributes to an assessment of the accuracy of the measured geomechanical model (Gholilou et al. 2017). The stresses applied to the rocks underground are almost identical in various directions under isotropic conditions and before well drilling (SV = Shmin = Shmax). However, these values change after drilling and these changes are more noticeable on a significant regional scale in active tectonic areas such as anticlines, fault-adjacent areas, salt domes, and other active tectonic areas. Mechanical failures in the wellbore are induced by adjusting the horizontal stress values. These mechanical failures can be in the maximum horizontal stress direction in the form of tensile failures or breakdown, and shear failures or breakouts are in the minimum horizontal stress direction which both are produced roughly parallel to the wellbore axial. Using acoustic and density logs, as well as reservoir properties like Poisson's ratio, vertical stress, and pore pressure, the stress profile in the reservoir is determined (Almalikee and Al-Najim 2018). There are many methods to assess the direction and location of these stresses. Image logs are one of the most detailed methods to classify the features of these stresses. Figure 7 shows the location and direction of breakouts created by shear stress observed on the FMI log. These breakouts were also recorded using caliper logs (C1 and C2). Three breakout zones by calipers and FMI logs are displayed in Fig. 7.
Orientation of breakouts observed by FMI log. From right: first column is orientation of observed breakouts, second column shows location and direction of each breakouts, third column shows breakouts on FMI log, fourth column shows the effect of breakouts on caliper logs and the last column is depth
The minimum horizontal stress (Shmin) can be determined directly from the minifrac test, hydraulic fracture, or LOT/XLOT test; however the maximum horizontal stress (Shmax) cannot be computed directly. Even though both of them can be calculated using indirect methods with acceptable accuracy. The poroelastic stress equation is used in conventional ways to estimate the minimum horizontal stress gradient as a function of vertical depth. The theory of poroelasticity, which explains how a lithified, porous medium-like rock deforms when the pore space is filled with fluid and pressurized, describes the fluctuation of Sh as a function of Pp (Kümpel 1991). One of the most often used approaches in the industry for determining horizontal stresses under isotropic conditions is the poroelastic method. Changes in elastic stiffness characteristics caused by structural anisotropy are used to predict the minimum and maximum horizontal stresses in this method (Abdelghany et al. 2021; Maleki et al. 2014). As a result, one of the conventional methods for indirectly determining minimum and maximum horizontal stresses is to employ the poroelastic method. (Blanton and Olson 1997):
where ν is the Poisson's ratio, α is Biot coefficient, PP is pore pressure, E is the static Young's modulus, ε is the tectonic strain in the x and y directions (Aghajanpour et al. 2017). Model prediction and calibration with wellbore data (observed breakouts on FMI or caliper logs) were used to identify these tectonic strains. Biot coefficient or effective stress coefficient (α) can be calculated using various parameters such as bulk modulus (Biot 1941), porosity (Krief et al. 1990), and permeability (Klimentos 2003). Theoretically, it is in the range of 0–1 (0 ≤ α ≤ 1). This parameter is normally derived from the following equation:
where Kb is volumetric parameter of the rock total volume and Kg is volumetric parameter of the rock grains. The Biot coefficient was considered 1 in this analysis. If LOT/XLOT is available, the horizontal stresses are adjusted to determine the actual tectonic strain values (Gholami et al. 2015; Zoback 2010). The εx and εy values should also be varied in such a way that the horizontal stress curve at least matches the single values obtained from the field tests as much as possible. In fact, the true value of this parameter is obtained by calibrating the minifrac, LOT/XLOT, and other calibration data with minimum horizontal stress (Shmin) and can be ensured by stress values. Table 1 presents the outcome of the leak-off test in a nearby well under various casing shoe sizes. As can be shown, not all experiments have overcome the rock failure pressure and were conducted as FIT due to the constraint of casing burst. (As the depths of these tests are not in the interval of the analysis, their gradients were used to calibrate the stress.).
Wellbore stresses
Generally, two key sets of stresses including far-field stresses and wellbore stresses, should be considered for wellbore stability analysis. Usually, in situ stress is divided into three parts: vertical stress, minimum horizontal stress, and maximum horizontal stress. The formation rocks are in front of the field stresses before drilling, but after drilling these rocks are pushed out in the cutting form and the wellbore must withstand the stresses of the field. These stresses relate to the well-trajectory as well as the impact of the field dominant stress on the well-drilling location (Nelson et al. 2006). The equilibrium of in situ pressures around the wellbore is compromised as a consequence of well drilling. Based on the interruption in the distribution of stresses near the wellbore, three different stresses are defined within the wellbore. These turbulent stresses are referred as induced stresses or intra-well stresses. Induced stresses are stresses which formed after drilling and around wellbore. Their amount is greater than initial stresses and they will cause shear or tensile failure if the amount of these stresses exceeds the strength of the rocks. Therefore, their quantity needs to be measured and confirmed. There are three types of induced stresses: tangential stresses (acting in the tangential direction of the wellbore), radial stresses (parallel to the radius of the well), and axial stresses (in the direction of the well axis and vertically to the center of the earth) (Fig. 8).
The quantity of these stresses is a function of the ratio of well radius to distance from the wellbore and can be defined easily in a well-coordinated system. These three induced stresses are perpendicular to each other and with an increase in the distance from center of the well, stress decreases since the ratio of radius to the distance decreases. These stresses are equal to the initial stresses at very long distances. Measurement of such stress values has been presented in the vertical and directional wellbore (Aadnoy and Looyeh 2019; Kirsch 1898). The following equations are for a vertical well:
where: Sr is radial stresses, Sz is axial stresses and Sθ is tangential stresses, PP is the pore pressure, Ph is the hydrostatic pressure in Pascal. θ is also equivalent to the desired point azimuth (degree) with the horizontal stress direction taken into account. In vertical wells, maximum tangential stress (Sθ (max)) occurs in the direction of minimum horizontal stress (i.e., θ = 90˚) and minimum tangential stress (Sθ (min)) occurs in the direction of maximum horizontal stress (i.e., θ = 0˚). The following equations can be used to approximate two tangential stresses (Kirsch 1898):
Failure criteria
Many of the failure criteria have been proposed: Mohr–Coulomb (Coulomb 1973), Mogi-Coulomb (Mogi 1971), Hoek–Brown (Brown and Hoek 1980), and Single-Parameter parabolic failure criteria (Li et al. 2005). It should be noted that the most common cases in the normal Breakout and Breakdown stress regime are Sθ > Sz > Sr and Sr > Sz > Sθ (Al-Ajmi 2012; Gholami et al. 2014). Several researchers have identified some problems related to the estimated values of rock strength or lack of adequate knowledge of stress levels in the estimated stress values for failure criteria (Song and Haimson 1997; Vernik and Zoback 1992). The Mohr–Coulomb failure criterion is one of the failure criteria that is commonly used in oil industry due to better efficiency in terms of time and its linear consistency (Gholami et al. 2017, 2014, 2015). Of course, by ignoring the impact of intermediate stress and using the minimum and maximum stress values, this failure criterion is used only to measure the maximum mud pressure for wellbore stability. This criterion's mathematical relationship focused on the main stresses is as follows (Mohr 1900):
The Mohr–Coulomb failure criterion's linearity is presented as follows (Tan et al. 2019):
where S1 and S3 are the main maximum and minimum stresses and SC is unconfined compressive strength. The following equation describes the relationship between normal and shear stress when two adhesion coefficients and internal friction angle factors are used in this criterion:
where τ is the shear stress, ϕ is the internal friction angle, Sn is the normal stress and C is the adhesion coefficient. Table 2 presents the calculation of mechanical failure stresses (Breakout and Breakdown) using the Mohr–Coulomb failure criterion in various modes of induced stresses.
Two internal friction angles and adhesion coefficient are significant parameters defined by the Mohr–Coulomb failure criterion. It is used to determine these two parameters in the laboratory through three-axis testing on drilling core samples. But there are also empirical relationships in which it is possible to quantify these parameters. The following equations are provided to quantify these two parameters:
where: ϕ is internal friction angle, NPHI is neutron porosity, Vshale is shale volume (usually calculated from the Gamma-Ray log), UCS is uniaxial stress and C represents the adhesion coefficient.
Result and discussion
Wellbore stability and safe mud window
The wellbore stability and safe mud window were analyzed after determining the various stresses in the wellbore. The results of the stress analysis are shown in Fig. 9. The fault regime is commonly strike-slip and normal at some depths, according to computed stresses. Kick (pore pressure), shear failure or breakout, loss (minimum stress), and tensile failure or breakdown are four wellbore stability analysis ranges described for determining the safe mud window. In this analysis, there was no information on equivalent pressure in the mud window (ECD). A coefficient of 1.03 was used to convert the static mud weight into a dynamic equivalent pressure. The mud weight used for drilling in the studied interval is 11.8 (ppg). It should be noted that 1 pound per gallon (ppg) is equivalent to 7.48 pounds per cubic foot (pcf). Figure 9 indicates that the mud weight used is very close to the shear failure or breakout limit and that the mud weight is lower at depths such as 2655 and 2775 m and there has been shear failure (breakout). Shear failures can be avoided in order to solve this issue in nearby vertical wells that will be drilled in the future, by increasing the mud weight by one to two pounds per cubic foot. The model prediction of shear failure is observed in the 6th column of Fig. 9 (failure image column). Due to the direction of local stresses and their interaction with the wellbore, the azimuth and deviation of the drilling well can affect the stability of the wellbore. As a result, the safe mud window of a vertical well may change for deviated wells, and sensitivity analysis at any depth is required to establish the appropriate deviation and azimuth. Figures 10, 11 and 12 demonstrate sensitivity analysis at selected depths. The four mentioned categories (breakout, kick, loss, breakdown) are also presented based on azimuth and deviation in the fifth column shown in Fig. 9. For each azimuth and each deviation from the vertical location for both Breakout and Breakdown modes, the optimal mud weight is determined in stereonets. Figs. 10, 11, and 12 depict safe zones in terms of mud weight and drilling direction, indicating certain stable and unstable depths along the investigated well. The blue color in stereonets denotes the safe locations for drilling orientation without any breakout or breakdown (stable orientation), whereas the red color denotes the unstable orientation. The safe mud window is shown in white color in crossplots that show mud weight versus azimuth and deviation in a specific depth, whereas other colors such as gray, yellow, purple, and navy-blue indicate kick, shear failure (breakout), loss, and tensile failure (breakdown). The mud weight employed at that depth is shown by the point marked on these cross-plots. The optimal deviation, azimuth, and mud weight are provided in Table 3 to prevent shear and tensile failures at depths where sensitivity analysis has been carried out.
Geomechanical model and wellbore stability boundaries calculated. From right side: first column is static FMI. Second column shows failure images. Third column shows shear failure minimum pressure (CMW_MIN_MC), kick pressure (CMW_KICK), mud loss (CMW_LOSS), breakdown pressure (CMW_MAX_MTS), mud weight (MW_pcf and MW_ppg), minimum and maximum mud weight (MIN_MW and MAX_MW). Fourth column shows maximum horizontal stress (SHMAX_PHS), minimum horizontal stress (SHMIN_PHS), pore pressure points from MDT (Pp2), pore pressure log calculated from MDT points (PPressure_Final) and vertical stress (Sv). Fifth column shows uniaxial compressive strength (UCS), tensile strength (TENS_ST), static Young's modulus (YMSta), static Poisson's ratios (POIS_STATIC) and friction angle (FANG_FromGr). Other column explained in Fig. 6
Wellbore stability analysis by AI and RC
Sonic and density logs are utilized in a well to determine the acoustic impedance (AI), which is used to establish the reflection coefficient (RC). This is referred to as forward modeling. The fundamental data from continuous velocity surveys in wells can be used to simulate fluctuations in acoustic impedance in the ground that cause seismicity under certain simplified but reasonable physical assumptions. Acoustic impedance is an important property of rocks and geological layers. This parameter, which is the product of velocity and density, is a rock attribute that is often used to characterize reservoirs. In other words, this parameter is the most significant seismic feature of the seismic section. As a result, both AI and RC logs are susceptible to changes in the properties of drilled layers in the wellbore.
Acoustic impedance (AI)
Acoustic impedance is the resistance of a rock to elastic wave propagation. Acoustic impedance pseudologs are rock parameters that can reveal lateral changes in lithology as well as basic rock properties such as porosity and pore fill. Various formations have different lithologies, and these lithological differences, as well as different petrophysical properties, cause the acoustic impedance in a series of formations or rocks to differ from other formations or rocks. The establishment of a relationship between seismic and well log data is one of the most significant steps in seismic interpretation. The acoustic impedance log is computed from well data and used to verify the quality of seismic data at the well scale and extended to seismic cube the acoustic impedance log is produced by multiplying density and velocity:
The density log is typically taken along with the compressional and shear slowness logs in a hole. As a consequence, the compressional and shear impedance is determined using Eqs. 28 and 29 along the well:
where AIC and AIS are compressional and shear impedance, DTC and DTS are compressional and shear slowness and RHOB is bulk density log. Calcite and shale make up the lithology of the investigated interval. The density of the calcite layer is 2.71 (g/cm3), and the travel time (sonic) is between 45.5 and 47.5 (us/f). Density and transit time are more varied in shale layers. The density of middle-shale is 2.6 (g/cm3), and the transit time ranges from 60 to 170 (us/f). However, these figures are subject to change due to petrophysical characteristics like porosity, clay type, structure, and so on. As a result, computed acoustic impedance can be affected by a variety of circumstances, which will be discussed in the following sections.
Reflection coefficient (RC)
The resulting acoustic impedance log, on the other hand, was used to produce a reflection coefficient log (RC). By altering the velocity and density of the next layer, the acoustic impedance value changes at the layer boundary. The acoustic impedance value has a greater effect on the layer's change in velocity than the layer's change in density. The presence of fluids and the type of fluids in compression and shear velocity will also be effective (especially shear velocity). Seismic waves are often reflected from any boundary where the acoustic impedance varies. The magnitude of this reflection depends on the difference between two layers acoustic impedances and is derived from the following equations for the compression and shear impedances:
where RCC and RCS are compressional and shear reflection coefficient, AI1 is the acoustic impedance for layer 1 and AI2 is the acoustic impedance for layer 2. A schematic of forward modeling and lithological corrections is shown in Fig. 13.
The density and velocity of layers increase with increasing depth. As a result, the reflection coefficient of the layers would be a positive value. In conditions where the velocity and density of the layers are reduced, negative reflection coefficients are seen. Generally, there is a variation in acoustic impedance in layer boundaries that are distinct in terms of petrophysical and lithological properties and therefore a change in the reflection coefficient log. Low-speed layers, such as shale layers and porous layers, are factors that decrease the velocity of layers and thereby reduce their acoustic impedance. The reflection coefficient log is derived from the acoustic impedance log in the well which is calculated by the two density and sonic logs. Determined acoustic impedance from logs can have higher consistency and resolution than seismic data due to the sampling rate of log data relative to seismic sections, and its reading changes are influenced by the smallest changes in the wellbore.
The AI log is affected by a variety of parameters that influence the sonic and density logs. The RC log is equally susceptible to sudden changes in the reading of the AI log. Typically, hole condition and wellbore damage induce uncertainty in log readings, particularly for pad-base equipment like density tools. In such conditions, the effect of pad-base tools is minimized, and graphic well logs (GWL) are employed for petrophysical examination of these zones. In geomechanical modeling, these intervals (wellbore damage) are unstable zones. As a result, unstable zones are defined as intervals that have damage for any reason, and this damage produces noise in the reading of AI and RC records. This noise is regarded as an instability on AI and RC logs. The behavior of AI and RC logs in stable zones, as well as in unstable zones, will be examined in this part to study the likelihood of wellbore destabilizing variables such as kick, loss, shear, and tensile failures. AI and RC logs are used to investigate two aspects that influence well instability.
Layering
After calculation of the AI and RC logs for both compression and shear slowness and matching the behavior of these logs with the geomechanical model, there was an important association between the wellbore behavior in stable and unstable states and the behavior of these logs. A section of the wellbore is shown in stable and unstable states in Fig. 14.
The shear failure occurred so resulted in the breakout at the two specified depths in Fig. 14 (2650–2665 and 2683–2693). Based on the results of geomechanical analysis, the mud weight applied in both depths is lower than the safe mud window. There is a stable zone between these two depths. Some clay minerals (shale layers) along with limestone layers (particularly in the upper part) can be seen according to the lithology column obtained from the petrophysical evaluation. The difference in density and especially velocity between two limestone and shale layers in these sections causes a difference in acoustic impedance between the layers and can be seen very well sharp-reading changes on AI and especially RC logs. Caliper logs (C1 and C2) record the washout at these two depths, and due to the presence of breakouts in these depths and the absence of proper interaction between the pads and flaps with the borehole wall, the FMI log shows a distorted image. In response, the difference in density and velocity between these two depths is due to the presence of shale layers between the limestone layers which is shown in Fig. 15. Acoustic impedance and reflection coefficient logs confirm the velocity difference. The presence of these low-velocity layers (shale layers) between the limestone layers that can be identified on AL and RC logs indicates the shear failure zones. The mud weight applied in these zones is lower than the safe mud window. As a consequence, the threshold for mud loss and also the threshold for tensile failure in these regions is greater than other depths.
A zone with stable conditions is observed at a depth (2665–2683) between two unstable zones in Fig. 14. In this part of the well, AI and RC logs for both compression and shear slowness do not record sharp-changes in readings in this zone and display homogeneity and absence of layers with different velocities. This depth has approximately clean limestone and low porosity in terms of lithological characteristics and porosity. Both acoustic impedance and reflection coefficient logs related to compressional and shear slowness in this zone indicate uniform behavior. Low porosity and absence of storage capacity in this interval resulted in low fluid in the rock so no major difference in shear compared to compressional slowness as a result, both compression and shear slowness-related AI and RC logs show similar behavior. The geomechanical model and wellbore stability analysis results indicate that when the mud weight increases, tensile failure will occur without causing mud loss, which is associated with low porosity. As a consequence, when observed AI and RC logs with almost constant behavior, the homogeneity of the layer and low porosity is calculated. This feature reflects the stable wellbore, and it is a zone vulnerable to tensile failure without the initial loss of the drilling mud if the mud weight is increased. In terms of shear failure conditions in lower mud weight, this zone will also be more stable than other zones.
In Fig. 16, the AI and RC logs (for compressional wave only) were compared to the shear failure threshold (Breakout) log at a given depth (as shown in Fig. 14). Due to the geomechanical model, cross-plots have been drawn for two zones with unstable wellbore conditions (green color 2650–2665 and Turquoise color 2683–2693). In these zones, AIC and RCC values are scattered, which is also true for AIS and RCS due to their identical behavior in these two zones. The presence of shale thin layers with lower velocity and density between the limestone layers, which causes different values of acoustic impedance and increases the possibility of shear failure, is one of the most important explanations for the variable behavior of AI and RC logs in these zones. Also, in the RC versus CMW_MIN_MC cross-plot, the values of the RC log show a deviation of more than zero in these two zones. This implies the presence of layers with varying velocity and density properties and sharp-reading changes on AI log. In comparison, a layer with stable conditions exists between these two zones (blue color 2668–2680), and cross-plots for this zone show stable behavior for both AI and RC logs. The homogeneity of the layer is demonstrated by RC log with values near zero in this zone. It is observed that the probability of collapse and shear failure is reduced in such conditions, but the threshold of tensile failure relative to the upper and lower intervals is slightly increased. The probability of tensile failure in this zone will be higher than in the two zones above and below if the mud weight increases.
As the properties variation between adjacent layers is increased, the layering effect on wellbore stability becomes more noticeable. Because of the way acoustic impedance and reflection coefficient logs behave. Stable wellbore conditions are observed at the depth of 3013 to 3049 m (Fig. 17), and the AI and RC logs do not display the difference in acoustic impedance and hence the reflection coefficient (such as the depth of 2665–2683 in Figs. 14 and 16) and indicate the homogeneous condition region. However, in the lower sections, thin shale layers have formed despite no changes in porosity values, and the wellbore stable conditions are causing instability. Nevertheless, according to the geomechanical assessment, the lower sections of this interval containing the shale layers at a slower velocity than their upper and lower layers, have induced shear failure in the wellbore and the mud weight used is not within the safe mud window. On the AI and RC logs, the association of layers with a significant velocity difference is noticeable and displays an unstable region. The porosity in this section is also low and the low porosity decreases the threshold for tensile failure. When low-velocity interlayers (the shale layers shown in the lithology column), which behave differently than clean intervals, the behavior of the two AI and RC logs may be noticed. Shear failure is a risk in these zones.
As stated in the previous sections, in unstable intervals which occurred shear failure, readings of well logs are associated with noise and have high uncertainty in calculations. However, due to the fact that these zones are characterized as unstable zones in geomechanical modeling and presence of these evidences on AI and RC logs is considered as unstable zones too. But sometimes sharp changes in the reading of AI and RC logs, which are similar to changes in these logs at damage intervals (as in the lower part of Fig. 17), are also interpreted as unstable zones. According to well evidence and the results of various analyzes, the existence of layering with different properties can be one of the important reasons for shear failure and causes sharp-readings in AI and RC los. The mud weight in these zones should be applied with caution.
Layering Effect on Seismic Section
The reflection coefficient determines the layering changes on seismic sections. The reflection coefficient acquired from seismic sections can detect these changes with less resolution than well logs. The RC logs for compressional and shear on the seismic section in the examined interval are shown in Figs. 18 and 19. We increased the gain from 100 to 500 because the reflection coefficient log has low values and to better present it on seismic sections. Check-shot data, on the other hand, was used to convert their depth scale to a time scale. On seismic sections, intervals with high reflection coefficients can be introduced as unstable intervals, and these intervals can be prone to shear failure.
Porosity
Porosity is one of the most important factors to consider while analyzing wellbore stability. Changes in porosity values along the well have an impact on the four zones described in the wellbore stability analysis: kick, loss, breakout, and breakdown. Figure 20 depicts three zones with varying porosity and wellbore conditions, as well as how AI and RC log behavior is interpreted in each zone. The wellbore is stable according to the considered mud weight in all three intervals but porosity variations in these zones have modified the behavior of the four analyzed areas relative to each other and to the porosity parameter.
The AIc and AIs logs in section A have higher acoustic impedance values than section B. Section B also have higher acoustic impedance values than section C, which is due to the common lithology characteristics of the three areas in each of these three zones (clean limestone), the porosity values in these zones are directly related to changes in acoustic impedance values. The acoustic impedance values decrease as the porosity increases slowly, indicating that these zones are low-velocity zones. However, the behavior of RCc and RCs in all three zones by changing the porosity values, does not show much change and shows values close to zero. These three zones are homogeneous in terms of visible changes in velocity and density but they have different porosity values than each other. As a consequence, in homogeneous zones porosity values may play a more important role in wellbore stability analysis. Rising porosity from zone A to C increases the probability of shear failure or breakout, so higher porosities increase the probability of shear failure, thus increasing porosity reduces the probability of tensile failure or breakdown, but exacerbates the issue of fluid loss. Figure 21 shows KICK-BREAKOUT log (difference between Shear Failure and Kick) and LOSS-BREAKDOWN log (difference between Loss and Tensile Failure) versus porosity derived from petrophysical analysis in all of the studied interval. These logs actually show the amount of shear failure to kick (KICK-BREAKOUT log) and loss to tensile failure (LOSS-BREAKDOWN log). It has been discovered that increasing porosity increases the shear failure zone to the kick as well as the tensile failure zone.
According to the marked depths along the well and on the cross-plots, A, B, and C which are the areas shown in Fig. 21, shows an almost linear behavior with increasing porosity. In porosity versus tensile failure cross-plot (PHIE vs. LOSS-BREAKDOWN) shows that as the porosity increases, the difference between the tensile failure threshold log (CMW_MAX_MTS) and loss log (CMW_LOSS) increases. This means that as porosity increases, fluid loss increases and the probability of tensile failure decreases. In contrast, porosity versus shear failure cross-plot (PHIE vs. KICK-BREAKOUT) shows that as porosity increases, the risk of shear failure rises as well. As a consequence, the relationship between porosity and shear failure is direct, while the relationship between porosity and tensile failure is inverse. Figure 22 shows the relationship between compressional and shear impedance and effective porosity over the entire interval, with three A, B, and C zones characterized by differing porosity and acoustic impedance.
Figure 22 shows zones with low porosity and high acoustic impedance that have a low risk of shear failure but a high probability of tensile failure. The kick phenomena will occur in these zones as the mud weight decreases, and tensile failure is likely as the mud weight increases without loss. B are zones with medium porosity and acoustic impedance in comparison to other zones, in which four phenomena of kick, loss, shear, and tensile failure are feasible. C zones with high porosity and low acoustic impedance are zones with a high likelihood of shear failure and loss and a low probability of tensile failure. In these zones, if the mud weight goes below the safe mud window, breakout will occur fast, and if the mud weight rises over the safe mud window, substantial mud loss will occur, with a very low chance of tensile failure.
Conclusion
One of the most important studies in reducing drilling activity costs and risk is the wellbore stability evaluation in developing fields. A carbonate reservoir interval in one of the developing fields was investigated in the present research. The calculated values of in situ stress showed that the fault regime is often strike-slip and normal at some depths. For this reservoir, wellbore stability analysis was performed using the failure criterion of Mohr–Coulomb. The results showed that except for short sections, the applied mud weight in this hole was in the safe mud weight window. The sensitivity analysis for geomechanical model at certain depths also showed the optimal range of azimuth, deviation, and mud weight. As a result, the minimum and maximum optimal mud weight is between 10 and 16 ppg for this hole, which changes this range at certain intervals.
Using density and sonic logs, AI and RC for compressional and shear slowness were calculated. The behavior of AI and RC logs beside of geomechanical model showed that the association of layers with different velocity and densities along the well that can be reported by these logs are intervals from the well that are sensitive to shear failure or breakout, and the mud weight should increase at these intervals than other intervals. The zones with constant AI readings and RC values close to zero have homogeneous intervals, but as the mud weight increases in poros zones, these zones have a higher mud loss threshold and less tensile failure than other zones, indicating that the porosity function is very significant here. In homogenous zones with low porosity, increasing the mud weight can cause tensile failure without fluid loss in the formation, which is characterized by low and consistent AI log values and RC log readings close to zero.
Since there are no layers with different properties in homogeneous zones, there is no change in the behavior of the RC log, then the AI reading range will determine the type of potential unstable factor of the wellbore. As a result, as porosity increases, the shear failure threshold (Breakout) increases, and there is a direct relationship between porosity and shear failure threshold. Conversely, increasing porosity lowers the tensile failure (Breakdown) threshold, and the two have an inverse relationship, whereas mud loss is exacerbated. As a result, it is feasible to evaluate the areas prone to kick, loss, shear, and tensile failures to wellbore stability analysis and conduct more extensive planning in these zones by taking a quick check at the behavior of the two AI and RC logs.
Abbreviations
- AIc:
-
Compressional acoustic impedance
- AIs:
-
Shear impedance
- RCc:
-
Compressional reflection coefficient
- RCs:
-
Shear reflection coefficient
- S v and S n :
-
Vertical stress and normal stress
- PHIE:
-
Effective porosity
- DTc and DTs:
-
Compressional slowness and shear slowness (sonic log)
- FMI:
-
Formation micro imager
- DSI:
-
Dipole shear sonic imager
- MDT:
-
Modular formation dynamics tester
- ρ and ρ b and RHOB:
-
Density
- D and Z and dz:
-
Depth
- g :
-
Gravity
- tvd:
-
True vertical depth
- P h :
-
Hydrostatic pressure
- P P :
-
Pore pressure
- E dyn and E sta :
-
Young dynamic modulus and young static modulus
- ν dyn and ν sta :
-
Dynamic Poisson ratio and static Poisson ratio
- K :
-
Bulk modulus
- G :
-
Shear modulus
- UCS:
-
Uniaxial compressive strength
- α and BIOT:
-
Biot coefficient
- Shmin and Shmax :
-
Minimum horizontal stress and maximum horizontal stress
- C1 and C2:
-
Caliper 1 and Caliper
- LOT/XLOT:
-
Lake off test and extended leak off test
- ε :
-
Tectonic strain
- FIT:
-
Formation integrity test
- Sθ and Sz and Sr:
-
Tangential stress and axial stress and radial stress
- C :
-
Adhesion coefficient
- φ :
-
Internal friction angle
- NPHI:
-
Neutron porosity
- V shale :
-
Shale volume
- V p and V s :
-
Compressional velocity and shear velocity
- CMW_KICK:
-
Kick pressure
- CMW_LOSS:
-
Mud loss
- CMW_MAX_MTS:
-
Breakdown pressure
- CMW_MIN_MC:
-
Shear failure minimum pressure
- MW:
-
Mud weight
- KICK-BREAKOUT:
-
Difference between shear failure and kick
- LOSS-BREAKDOWN:
-
Difference between loss and tensile failure
References
Aadnoy B, Looyeh R (2019) Petroleum rock mechanics: drilling operations and well design. Gulf Professional Publishing, London
Abdelghany WK et al (2021) Geomechanical modeling using the depth-of-damage approach to achieve successful underbalanced drilling in the Gulf of Suez rift basin. J Pet Sci Eng 202:108311
Aghajanpour A, Fallahzadeh SH, Khatibi S, Hossain MM, Kadkhodaie A (2017) Full waveform acoustic data as an aid in reducing uncertainty of mud window design in the absence of leak-off test. J Nat Gas Sci Eng 45:786–796
Al-Ajmi AM (2012) Mechanical stability of horizontal wellbore implementing Mogi-coulomb law. Adv Pet Explor Dev 4(2):28–36
Al-Ajmi AM, Zimmerman RW (2006) Stability analysis of vertical boreholes using the Mogi–Coulomb failure criterion. Int J Rock Mech Mining Sci 43(8):1200–1211
Almalikee HSA, Al-Najim FMS (2018) Overburden stress and pore pressure prediction for the North Rumaila oilfield, Iraq. Model Earth Syst Environ 4(3):1181–1188
Amani A, Shahbazi K (2013) Prediction of rock strength using drilling data and sonic logs. Int J Comput Appl 81(2):1–10
Bagdeli M et al (2019) Natural fracture characterization and wellbore stability analysis of a highly fractured southwestern Iranian oilfield. Int J Rock Mech Min Sci 123:104101
Baziw E, Ulrych TJ (2006) Principle phase decomposition: a new concept in blind seismic deconvolution. IEEE Trans Geosci Remote Sens 44(8):2271–2281
Biot MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12(2):155–164
Bjørlykke K, Høeg K, Mondol NH (2015) Introduction to Geomechanics: stress and strain in sedimentary basins, Petroleum geoscience. Springer, Berlin, pp 301–318
Blanton T, Olson JE (1997) Stress magnitudes from logs: effects of tectonic strains and temperature. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Brown E, Hoek E (1980) Underground excavations in rock. CRC Press, London
Coulomb CA (1973) Essai sur une application des regles de maximis et minimis a quelques problemes de statique relatifs a l'architecture (essay on maximums and minimums of rules to some static problems relating to architecture)
Darvishpour A, Seifabad MC, Wood DA, Ghorbani H (2019) Wellbore stability analysis to determine the safe mud weight window for sandstone layers. Pet Explor Dev 46(5):1031–1038
Das B, Chatterjee R (2017) Wellbore stability analysis and prediction of minimum mud weight for few wells in Krishna–Godavari Basin, India. Int J Rock Mech Min Sci 93:30–37
Eaton BA (1975) The equation for geopressure prediction from well logs. In: Fall meeting of the Society of Petroleum Engineers of AIME. Society of Petroleum Engineers
Gholami R, Moradzadeh A, Rasouli V, Hanachi J (2014) Practical application of failure criteria in determining safe mud weight windows in drilling operations. J Rock Mech Geotech Eng 6(1):13–25
Gholami R, Rasouli V, Aadnoy B, Mohammadi R (2015) Application of in situ stress estimation methods in wellbore stability analysis under isotropic and anisotropic conditions. J Geophys Eng 12(4):657–673
Gholami R, Aadnoy B, Foon LY, Elochukwu H (2017) A methodology for wellbore stability analysis in anisotropic formations: a case study from the Canning Basin, Western Australia. J Nat Gas Sci Eng 37:341–360
Gholilou A, Vialle S, Madadi M (2017) Determination of safe mud window considering time-dependent variations of temperature and pore pressure: analytical and numerical approaches. J Rock Mech Geotech Eng 9(5):900–911
Guo S, Wang H (2019) Seismic absolute acoustic impedance inversion with L1 norm reflectivity constraint and combined first-and second-order total variation regularizations. J Geophys Eng 16(4):773–788
Han Y, Liu C, Phan D, AlRuwaili K, Abousleiman Y (2019) Advanced wellbore stability analysis for drilling naturally fractured rocks. In: SPE middle east oil and gas show and conference. Society of Petroleum Engineers
Kassem AA, Sen S, Radwan AE, Abdelghany WK, Abioui M (2021) Effect of depletion and fluid injection in the mesozoic and paleozoic sandstone reservoirs of the october oil field, central Gulf of Suez Basin: implications on drilling, production and reservoir stability. Nat Resour Res 30(3):2587–2606
Khatibi S, Aghajanpour A, Ostadhassan M, Farzay O (2018) Evaluating single-parameter parabolic failure criterion in wellbore stability analysis. J Nat Gas Sci Eng 50:166–180
Kirsch C (1898) Die theorie der elastizitat und die bedurfnisse der festigkeitslehre. Zeitschrift Des Vereines Deutscher Ingenieure 42:797–807
Klimentos T (2003) NMR applications in petroleum related rock-mechanics: sand control, hydraulic fracturing, wellbore stability. In: SPWLA 44th annual logging symposium. OnePetro
Kong L et al (2019) Geomechanical upscaling methods: comparison and verification via 3D printing. Energies 12(3):382
Krief M, Garat J, Stellingwerff J, Ventre J (1990) A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic). The Log Analyst 31(6):27–35
Kümpel H-J (1991) Poroelasticity: parameters reviewed. Geophys J Int 105(3):783–799
Latimer RB, Davidson R, Van Riel P (2000) An interpreter’s guide to understanding and working with seismic-derived acoustic impedance data. Lead Edge 19(3):242–256
Le K, Rasouli V (2012) Determination of safe mud weight windows for drilling deviated wellbores: a case study in the North Perth Basin. WIT Trans Eng Sci 81:83–95
Li S, Rao Y (2020) Poroelastic property analysis of seismic low-frequency shadows associated with gas reservoirs. J Geophys Eng 17(3):463–474
Li C-G, Zheng H, Ge X-R, Wang S-L (2005) Research on two-parameter parabolic Mohr strength criterion and its damage regularity. Yanshilixue Yu Gongcheng Xuebao/chin J Rock Mech Eng 24(24):4428–4433
Li S, Peng Z, Wu H (2018) Prestack multi-gather simultaneous inversion of elastic parameters using multiple regularization constraints. J Earth Sci 29(6):1359–1371
Maleki S et al (2014) Comparison of different failure criteria in prediction of safe mud weigh window in drilling practice. Earth Sci Rev 136:36–58
Mandal A, Ghosh SK (2020) Estimating broad trend of acoustic impedance profile from observed seismic reflection data using first principles only. J Geophys Eng 17(3):475–483
Masoudi P, Tokhmechi B, Bashari A, Jafari MA (2012) Identifying productive zones of the Sarvak formation by integrating outputs of different classification methods. J Geophys Eng 9(3):282–290
Mogi K (1971) Fracture and flow of rocks under high triaxial compression. J Geophys Res 76(5):1255–1269
Mohiuddin M, Khan K, Abdulraheem A, Al-Majed A, Awal M (2007) Analysis of wellbore instability in vertical, directional, and horizontal wells using field data. J Petrol Sci Eng 55(1–2):83–92
Mohr O (1900) Welche Umstände bedingen die Elastizitätsgrenze und den Bruch eines Materials. Z Ver Dtsch Ing 46(1524–1530):1572–1577
Mondal S, Chatterjee R (2019) Quantitative risk assessment for Optimum Mud weight window design: a case study. J Petrol Sci Eng 176:800–810
Morozov IB, Ma J (2009) Accurate poststack acoustic-impedance inversion by well-log calibration. Geophysics 74(5):R59–R67
Nelson E, Hillis R, Mildren S (2006) Stress partitioning and wellbore failure in the West Tuna Area, Gippsland Basin. Explor Geophys 37(3):215–221
No E, Ehirim C, Nwosu J Analytical approach to reservoir property evaluation of a field in Niger Delta
Peng ZM, Li YL, Wu SH, He ZH, Zhou YJ (2008) Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs. Chin J Geophys 51(3):639–644
Radwan AE (2021) Modeling pore pressure and fracture pressure using integrated well logging, drilling based interpretations and reservoir data in the giant El Morgan oil field, Gulf of Suez. Egypt. J Afr Earth Sci 178:104165
Radwan A, Sen S (2021a) Stress path analysis for characterization of in situ stress state and effect of reservoir depletion on present-day stress magnitudes: reservoir geomechanical modeling in the Gulf of Suez Rift Basin, Egypt. Nat Resour Res 30(1):463–478
Radwan AE, Sen S (2021b) Characterization of in-situ stresses and its implications for production and reservoir stability in the depleted El Morgan hydrocarbon field, Gulf of Suez rift basin, Egypt. J Struct Geol 148:104355
Radwan A, Abudeif A, Attia M, Mohammed M (2019) Pore and fracture pressure modeling using direct and indirect methods in Badri Field, Gulf of Suez, Egypt. J Afr Earth Sci 156:133–143
Radwan A et al (2020) Geopressure evaluation using integrated basin modelling, well-logging and reservoir data analysis in the northern part of the Badri oil field, Gulf of Suez, Egypt. J Afr Earth Sci 162:103743
Radwan AE, Abdelghany WK, Elkhawaga MA (2021) Present-day in-situ stresses in Southern Gulf of Suez, Egypt: insights for stress rotation in an extensional rift basin. J Struct Geol 147:104334
Rana R, Chandrashekhar C (2015) Pore pressure prediction a case study in Cambay basin. Geohorizons 20(1):38–47
Shahbazi K, Zarei AH, Shahbazi A, Tanha AA (2020) Investigation of production depletion rate effect on the near-wellbore stresses in the two Iranian southwest oilfields. Petr Res 5(4):347–361
Song I, Haimson BC (1997) Polyaxial strength criteria and their use in estimating in situ stress magnitudes from borehole breakout dimensions. Int J Rock Mech Min Sci 34(3–4):116.e1-116.e16
Tan T et al. (2019) Analysis on collapse pressure and fracture pressure of a borehole in natural gas hydrate formation. In: 53rd US rock mechanics/geomechanics symposium. American Rock Mechanics Association
Vernik L, Zoback MD (1992) Estimation of maximum horizontal principal stress magnitude from stress-induced well bore breakouts in the Cajon Pass scientific research borehole. J Geophys Res Solid Earth 97(B4):5109–5119
Wang R, Wang Y (2017) Multichannel algorithms for seismic reflectivity inversion. J Geophys Eng 14(1):41–50
Xu D, Wang Y, Gan Q, Tang J (2011) Frequency-dependent seismic reflection coefficient for discriminating gas reservoirs. J Geophys Eng 8(4):508–513
Zhang J (2013) Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes. Int J Rock Mech Min Sci 60:160–170
Zoback MD (2010) Reservoir geomechanics. Cambridge University Press, Cambridge
Zoback M et al (2003) Determination of stress orientation and magnitude in deep wells. Int J Rock Mech Min Sci 40(7–8):1049–1076
Author information
Authors and Affiliations
Contributions
All authors have participated in (a) conception and design, or analysis and interpretation of the data; (b) drafting the article or revising it critically for important intellectual content; and (c) approval of the final version. This manuscript has not been submitted to, nor is under review at, another journal or other publishing venue. The authors have no affiliation with any organization with a direct or indirect financial interest in the subject matter discussed in the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The following authors have affiliations with organizations with direct or indirect financial interest in the subject matter discussed in the manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bagheri, H., Tanha, A.A., Doulati Ardejani, F. et al. Geomechanical model and wellbore stability analysis utilizing acoustic impedance and reflection coefficient in a carbonate reservoir. J Petrol Explor Prod Technol 11, 3935–3961 (2021). https://doi.org/10.1007/s13202-021-01291-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-021-01291-2