Introduction

Drilling fluid is considered as one of the most important segment in drilling industry. It is used in the oil and gas sector to provide numerous functions such as removal of the drill cutting, cool and lubricate the bit (Zakaria 2013; Al-Yasiri et al. 2019; Bayata et al. 2018; Abdo and Haneef 2011; Mao et al. 2015), maintain hydrostatic pressure, and assist in well logging operations (Zakaria 2013; Al-Yasiri et al. 2019; Abdo and Haneef 2011; Mao et al. 2015). Drilling fluid can be classified into three distinct categories, water-based drilling fluid (WBDF), oil-based drilling fluid and synthetic-based mud systems (SBMS) (Bayata et al. 2018). Though the latter two have some high operational competences, yet still their use decline considerably because of environmental issues associated with them (Bayata et al. 2018; Riley et al. 2012; Sharma et al. 2012; Khodja et al. 2010). As a result, the use of WBDF is preferred, despite suffering from some shortcomings. However, main drawback accompanied with the use of WBDF is drilling in a shale formation. This formation tends to swells when comes directly in contact with WBDF (Bayata et al. 2018; Aftab et al. 2020a; Al-Ansari et al. 2017). However, still almost 75% of the shale formations are drilled using WBDF (Aftab et al. 2020a; Murtaza et al. 2020) because this mud system is fairly inexpensive (Aftab et al. 2020a; Elkatatny et al. 2018) and environmentally friendly (Aftab et al. 2020a; Aftab et al.2017a; Murtaza et al. 2020).

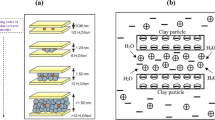
Shale is mainly classified as a clastic sedimentary rock (Díaz-Pérez et al. 2007), which comprises of silt, clay and mud in varying concentrations (Gholami et al. 2018; Moslemizadeh et al. 2015; Wang et al. 2020). The concentration of the clay mineral in shale formation is arranged either in the form of lamination (Díaz-Pérez et al. 2007; Moslemizadeh et al. 2015), structural or dispersed. Almost 90% of wellbore instability problem are as a result of these high clay contents (Moslemizadeh et al. 2015; Steiger and Leung 1992). The clay minerals consist of crystal platelets that are tetrahedral and octahedral in shape and are linked with oxygen atoms (Moslemizadeh et al. 2015). Swelling and disintegration of clay normally arises as a result of the weak bonding between different tetrahedral sheets (Gholami et al. 2018), Van der Waals attraction and the in situ stresses (Oort 2003). Based on the structure of these sheets and their surface charges, clay mineral is classified into three different groups such as kaolinite, illite and montmorillonite (Aftab et al. 2017a). Out of these three minerals, montmorillonite have the greatest tendency to swell because of the wide gap that exists between its platelets (Moslemizadeh et al. 2015; Aftab et al. 2020b; Aftab et al. 2017b). This clay mineral expands up to ten times of its original size (Swai 2020), thus, exhibits wellbore instabilities issues, which ultimately results in severe consequences in the form of loss of life or even abandonment of the well (Swai 2020).

Several researchers experimentally reveal the swelling characteristics of shale formation. Darley in 1969 studied the swelling and dispersion of shale (Maghrabi et al. 2013). Similarly, in 1989 Chenevert and co-workers studied the inhibition of shale when it comes in contact with WBDF under both ambient and downhole conditions (Maghrabi et al. 2013). It was recommended during their study that for the prediction of early time swelling-indicator test was the best (Chenevert and Osisanya 1989). Furthermore, CEC test was conducted for the determination of exchangeable ions in the shale rock (Chenevert and Osisanya 1989). Stowe et al. (2001) and Ghanbari and Naderifar (2016), perform the experimentation on the stability of shale matrix using pore pressure transmission test (Gholami et al. 2018). In recent years, the swelling of any shale formation can experimentally be determined by using linear dynamic swell meter that provides a swelling response with respect to different experimental time intervals (Maghrabi et al. 2013; Samir and Osama 2007; Khan et al. 2020).

Likewise, the computational modeling of the swelling of shale was also studied by numerous scholars. In 1998, Molenaar formulated constitutive model based on transport equation that reveals the interaction between the drilling fluid and shale swelling (Maghrabi et al. 2013). In similar year Huang using numerical simulation and modeling demonstrates shale swelling behavior when it comes in contact with the drilling fluid (Maghrabi et al. 2013). In 2003, Basma (2003) used the idea of sequential artificial neural networks to model swelling of shale sample. These neural network modeling requires extensive computation works, for that purpose utilization of conventional modeling techniques are always preferred. Maghrabi et al. in 2013 developed a time-dependent equation that was found to be best fitted with the swelling response yield by linear dynamic swell meter (LDSM). The equation was derived using the first order kinetics term along with the filtration loss term (Maghrabi et al. 2013). The equation comprises of three different parameters that includes, saturation swelling term, first order swelling rate term and the filtrate loss parameter. However, the major drawback that is associated with this equation is not taking into the account the effect of temperature, swelling time, clay content that is present in the shale sample and the experimental results obtained through LDSM.

It is a well-known fact that the quality of experimental results might be affected by numerous factors; therefore, reproduction of experimental results through reliable independent modeling technique is essential. The first order kinetic model developed by Maghrabi et al. (2013) in 2013 was the fundamental model that uses concept of curve fitting for the modeling of shale swelling through linear dynamic swell meter experimental results. However, the model does not incorporate some of the governing factors on which the shale swelling depends. For that reason, a new proposed model that comprises of some of governing factors developed in this study. Furthermore, the major advantage for the proposed novel equation is not only it is capable of estimating swelling of shale with respect to time but also has an additional feature of predicting swelling onset time, which is not reported in any of the previous studies conducted on shale sample. The novel equations and previously developed model are applied on the experimental datasets and performance analysis of both equations is carried out using graphical methods as well as statistical metrics and accuracies are compared.

Model development

Drilling mud using in the study

For the development of the model, one barrel of amine-based mud system was prepare in laboratory. This mud system was prepared using 303 mL of water in which 0.25 g of soda ash (Na2CO3) as water treatment water was added, and the mixture was stirred for 2 min. After that, 5 g of PAC-L as viscosifiers was added in the mixture and the solution was again agitated for 5 min. Next, 1 g of Xanthan gum as viscosifiers was added in the solution in powder form, and the solution was again blended for 5 min. Following this, 7% of amine solution that corresponds to 24.5 mL was added in the mixture. This material ensures the formation of filming layer on the metal surface that protects the metal from corrosion. Lastly, 60 g of barite that acts as weighing agent was added in the mud system to establish the desired mud weight. The solution was again agitated in Hamilton Beach Mixture for 30 min to get the desire consistency. For the validation of the model, the mud system was changed to salt polymer glycol mud system that comprises of 309 mL of water along with 11 mL of polyethylene glycol that acts as shale stabilizer and 0.5 g of partially hydrolyzed polyacrylamide (PHPA) in place of PAC-L. This material is used as wellbore stabilizer, which further inhibits the dispersion of clay cutting while transporting up to the surface. All the testing based on the two mud systems were performed according to API Recommended Practice 13B-1. Both the mud systems were also evaluated based on their stability. For that, both the mud system was kept at room temperature for 24 h in order to observe any segregation of the barite in the system. It was perceived that there was no significant change during the period of 24 h when the muds were at room temperature.

Data preparation and linear dynamic swell meter (LDSM) test

There are several factors that are responsible for the swelling characteristics of a shale formation. These factors include time of the interaction between the water-based drilling fluid and the shale sample, weight percentages of clay minerals especially kaolinite, illite and montmorillonite in shale sample and temperature of the environment. Therefore, for the accurate development of the model these factors are taken into the consideration. The experimental data set was collected from a research study conducted on a sample of Murree shale formation that was prepared at 8000 psi (Lalji et al. 2021). From quantitative X-ray diffraction, it was observed that this formation comprises of 26% clay content. This 26% were further classified into 5.7% Illite, 6.7% of Kaolinite and remaining 13.6% of montmorillonite. The swelling percentage as indicated in Fig. 1 was obtained using OFITE LDSM (Model 150-80-230V). Based on the standard procedure, 15 g of formation was placed in a pressurized compactor at 8000 psi for the standard time of 1.5 h to form pellets for testing. The swell meter cells were then properly calibrated using the standard calibration procedure. After this process, each pellet was placed in swell meter cell that comprises of 20 mL of drilling fluid (Lalji et al. 2021). Similar procedure was followed for the Khadro formation that is used for the validation of the proposed model. This formation was acquired from the study of Khan et al. (2020) and was prepared at 6000 psi. Figure 2 indicates the swelling percentage of Khadro formation obtained using OFITE LDSM. This formation also comprises of 26% clay content that was further subdivided into 11% of Montmorillonite, 9% of Kaolinite and 6% of Illite (Khan et al. 2020). The effect of stresses and pressure were not studied during the experimentation. As mainly linear dynamic swell meter works on the concept of deducing the change in height of the sample through the use of transducer.

Fig. 1
figure 1

Swelling percentage of Murree shale formation obtained from linear dynamic swell meter (Lalji et al. 2021)

Full size image
Fig. 2
figure 2

Swelling percentage of Khadro shale formation obtained from linear dynamic swell meter (Khan 2020)

Full size image

First-order kinetic model for swelling model (EXISTING MODEL)

This existing method for the modeling of LDSM test results was developed in 2013 by Maghrabi et al. (2013). The equation for the shale swelling was derived by using the saturation swelling volume denoted by A, first order swelling rate denoted by B, which shows the number of available positions for swelling to progress and filtration loss parameter indicated by symbol C (Maghrabi et al. 2013). Equation (1) shows the Maghrabi et al. equation for the swelling

$$ \% S\left( t \right) = A\left( {1 - \frac{1}{{e^{Bt} + C\sqrt t }}} \right) $$
(1)

The swelling characteristics parameters A, B and C are attained by fitting the Eq. (1) on the curve of linear dynamic swell meter experimental results (Maghrabi et al. 2013). Here, the saturation swelling volume (A) is dependent on the cation exchange capacity (CEC) of the shale sample and the first order rate parameter (B) is reliant on the viscosity of the water-based mud system. While the filtrate loss parameter denoted as (C) was assigned a value between 0 and 1, since this parameter significantly contributes during the early stage of contact between the mud and shale sample (Maghrabi et al. 2013). The above-mentioned parameters are generally called as tuning parameters, which are modified according to the composition of water-based drilling fluid. As a matter of fact, as shown in Fig. 3, when this first order kinetic model was used to verify the quality of the results for the Pakistan shale formation, it was found out that swelling results were not in good agreement with the experimental datasets. The difference between the two datasets was because of missing of some of the vitals parameters in the modeling equation. These parameters include clay contents, temperature and the experimental results obtained through the swell meter. As an alternative, the proposed model is derived that demonstrates a better verification of the experimental results.

Fig. 3
figure 3

Modeling of Pakistan's shale formation using first order kinetic equation

Full size image

Proposed scaling swelling equation (NEW MODEL)

As discussed earlier, several inadequacies are associated with previously generated model by Maghrabi et al. (2013). To resolve this issue, an attempt is made to develop a reliable model that can take into consideration all the factors which were not present in the first order kinetic equation. The proposed model is developed by taking inspiration from the approach used by scaling equation applied for modeling asphaltene precipitation in dead oils (Gholami et al. 2013). The graphs obtained in asphaltene precipitation modeling between dilution ratio and weight percent follows a similar trend as the exponential distribution curve. All the graphs start to increase at a very small dilution ratio and then get parallel with the x-axis at higher ratio. Swelling of the shale in linear dynamic swell meter follow somewhat similar pattern. With this analogous behavior, it was suggested to use scaling model that collapse the curves of swelling rate and temperature change versus time obtained through linear dynamic swell meter into a single curve.

The main motivation features for adopting this approach are the high accuracy of scaling equations, less complexities in terms of computation, and the most importantly the similarity of experimental results (Rassamdana et al. 1996). Asphaltene precipitation is one of the major flow assurance problems of oil industry and in laboratory condition the dead oil potential to precipitate asphaltene is routinely checked by adding precipitants (n-alkanes) such as n-pentane and n-hexane. Scaling equations used experimental data which mainly include dilution ratio between crude oil and precipitant, weight percentage of asphaltene precipitated, experiment temperature and precipitant molecular weight. Though, the first scaling equation was developed by Rassamdana et al. (1996) in 1996 but after that there are large number of scaling equation were introduced by different investigators (Jamialahmadi and Ahmadi 2003). In this study, the approach applied by Ashoori et al. is adopted (Jamialahmadi and Ahmadi 2003). Ashoori et al. used four experimental parameters to model asphaltene precipitation which include precipitant molecular weight (asphaltene promoter), experimental temperature (less sensitivity on precipitation), dilution ratio of precipitant to oil that is considered to be directly proportional to precipitation till certain ratio and then become constant, and the weight percent of experimental precipitated asphaltene (final outcome).

During this study, three of the variables were monitored during the experimentation of shale swelling through OFITE LDSM. These parameters are experimentation time, temperature of the cell and the swelling percentages of the shale sample during its contact with the mud. However, a fourth parameter specifically the clay content, which is associated with the shale rock, was also determined during the study through QXRD reports. Since the linear dynamic swell meter experiment was performed at room temperature hence, temperature during the modeling was consider less sensitive as it do not changes significantly during experimentation. Furthermore, if a shale sample is tested at a temperature greater than 0 °C it demonstrates a lower swelling potential than those tested at a temperature below 0 °C (Huang et al. 1995). Moreover, the clay content was also made part of this model. This content is basically the aggregate of all the clay minerals weight percent obtained through QXRD reports. It is generally observed that greater the percentage of the clay content more will be the swelling in the shale sample; hence, for this particular reason it was made part of the model. Lastly, since the experimentation performed through the use of linear dynamic swell meter that is monitoring the result based on time, therefore, the use of contact time between the mud and shale sample was also made part of this equation.

To develop the proposed scaling swelling equation the four parameters are combined into two new variables X and Y as given below in Eqs. (2) and (3). Here t, T, C and S represents time, temperature, clay content and experimental swelling percentage obtained through OFITE LDSM and QXRD reports respectively.

$$ X = \frac{t}{{T^{n} * C^{{a_{1} }} }} $$
(2)
$$ Y = \frac{S}{{t^{{a_{2} }} }} $$
(3)

Moreover, a1 and n are the adjustable parameters while a2 = −2 is defined as a universal constant. All these are fine-tuning parameters that are selected for the purpose of achieving good fitting modeling results of the experimental data. The experimental data that comprises of swelling percentages vs. time and temperature of the experiment vs. time is collapsed on a single curve represented between two variables namely X and Y as shown in Eqs. (2) and (3), which is epitomized very accurately by third degree polynomial as shown in Eq. (4). This equation is used to back calculate the experimental data of the linear swell meter. It was observed that a higher or lower polynomial equation than this Eq. (4) do not provide an appropriate fitting curve that corresponds to linear dynamic swell meter experimental results.

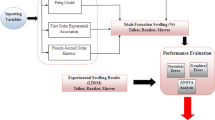
A1, A2, A3 and A4 in this equation are classified as scaling equation coefficients and Xc is the value of X at the onset/swelling initiation point of shale swelling. In order to obtain the onset point of swelling, the Xc need to be determined by substituting Y a value of 0 and then performing back calculation to obtain the tc (critical time). Critical time is the time at which swelling starts. To improve the performance of proposed model, the collapsing of data is done by splitting the dataset in terms of time. The splitting point is selected by looking at the behavior of curve between time and swelling. The time at which swelling increases abruptly is taken as splitting point. In this work, the splitting of experimental data is done at 1 h. Figure 4 shows the workflow for the proposed model developed in this study.

$$ Y = A_{4} + A_{3} X + A_{2} X^{2} + A_{1} X^{3} \;\;\;X \ge X_{c} $$
(4)
Fig. 4
figure 4

Workflow of the proposed scaling swelling model

Full size image

Performance evaluation of proposed scaling swelling equation

The performance of the proposed scaling swelling equation is evaluated using mean absolute error (MAE), mean square error and the root mean square error. The value of MAE, MSE and RMSE has been computed using Eqs. (5) to (7), where N is the number of data points, \(y_{i}\) is the calculated value and \(\widehat{{y_{i} }}\) is the experimental value (Ali et al. 2021).

$$ {\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {y_{i} - \widehat{{y_{i} }}} \right| $$
(5)
$$ {\text{MSE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {y_{i} - \widehat{{y_{i} }}} \right)^{2} $$
(6)
$$ {\text{RMSE}} = \sqrt {{\text{MSE}}} $$
(7)

For the in-depth study of the proposed scaling swelling equation, two graphical analyses techniques have been used. First a cross-plot is generated, which shows the relationship between the predicted values and the actual values. This plot comprises of a unit slope line that is established as a perfect model line (Ali et al. 2021). The accuracy of the predicted model can be determined if a higher percentage of the data points fall on to this perfect model line. Secondly, a relative error plot is generated, which determines the deviation between the predicted results obtained from the proposed model and the actual experimental results collected from linear dynamic swell meter results. The closer the peaks are to the x-axis the more consistency will be there between the model and experimental results.

Results and discussion

Implementation of the proposed scaling swelling equation

The experiment was carried out on Murree shale formation at a temperature of 25 °C. The curve shown in Fig. 5a, b represents a third degree polynomial relationship established between the two variables X and Y using Eq. (4). In the definition of X and Y, the temperature exponent ‘n’ and the parameter a1 in Eq. (2) are denoted as adjustable parameters that can be tuned depending upon the type of mud used in swelling experiment. Both of these parameters values lies within a range of 0.1 to 0.5. The coefficient a2 in Eq. (3) is treated as a universal constant having a value of −2 as already discussed in previous section. The collapse equation obtained between X and Y is shown in Eq. (4).

Fig. 5
figure 5

Collapse of swelling experimental data onto polynomial curve using the proposed scaling swelling equation a swelling is dominant b swelling is subservient

Full size image

It was observed from Fig. 1 that the maximum swelling occurred during the first few hours of the contact between the drilling mud and the shale sample; therefore, the swelling data was divided into two different regions with respect to swelling time. Figure 5a exhibits the region where swelling was dominant, while on the other hand, Fig. 5b displays the region where swelling was subservient. This division further improves the modeling results for the proposed model, as it was observed that both the cases reported a good fitting behavior. The best adjustable parameters in this case were obtained through MATLAB optimization tool, which ensures the accuracy of the proposed model by minimizing the error percentages. The variables in Eq. (2) were tuned with the values of a1 = 0.25 and n = 0.25 respectively. Table 1 shows the coefficient values of the collapse equation found for two cases after tuning the adjustable parameters. It was further observed that the value of R2 for both cases was close to 1, which is indicating the most appropriate fitting behavior relationship between the two variables X and Y.

Table 1 Coefficient of the collapse equation between X and Y
Full size table

Figures 6 and 7 show the sensitivity of adjustable parameters on the swelling percentages results. It was observed that increase in values of these adjustable parameters shows the deviation of the swelling result from the perfect model line. For this particular case, the optimum values for the adjustable parameters are in range of 0.1–0.5. Furthermore, it was witness that if the values of a1 and ‘n’ increases to 2, then negative swelling percentages were obtained, which indicates the poor performance of the proposed model. It was observed that when the values of adjustable parameters go beyond 0.5 or below 0.1, the parameters X and Y were not reporting a good fitting behavior. Therefore, when the collapse equation as shown by Eq. (4) was formed for those cases it was witnessed that R2 value was very low, thus, indicating a very small percentage of data sets falling on the perfect model line. Hence, it was concluded that the values of “a1” and “n” lies within the window of 0.1–0.5.

Fig. 6
figure 6

Sensitivity analysis for different a1 values

Full size image
Fig. 7
figure 7

Sensitivity analysis for temperature coefficient 'n'

Full size image

Figure 8 illustrates the swelling curve obtained from the experimental result, proposed model and the first order kinetic equation. It can be recognized from the figure that the proposed model almost produces a replica of the experimental results. It can further observed from Table 2 that the first order kinetic model under predict the final swelling result, which is not apparent for the proposed model. A deviation of 1.40% was observed in the final swelling result for the first order kinetic. On the other hand, for the new proposed model the final swelling result obtained shows concurrency with the experimentation results obtained from LDSM.

Fig. 8
figure 8

Swelling results from obtained from experimentation and modeling

Full size image
Table 2 Final Swelling % result
Full size table

Model accuracy

Figure 9 depicts the graphical demonstration of cross-plot for the swelling percentages obtained through two different models. It can be perceived from the result that for the new proposed model, a large portion of the datasets fall on the perfect model line, which clearly indicates the preeminence of the proposed model over the first order kinetic equation.

Fig. 9
figure 9

Cross-plot between the different models and the experimental dataset

Full size image

To quantify the difference in behavior of the two models a relative error plot of two models can be seen in Fig. 10, which exhibits the predicting swelling results with respect to time of the experiment. It can be observed that the first order kinetic equation demonstrates higher percentages of the relative error; while for the new proposed model the sizes of the relative errors histogram are very small, thus indicating an excellent performance. For the new model, at initial time interval the value of the relative error is maximum, however, this value does not significantly contributes to the overall error in the model. For the new model, it can further observed that out of 38 dataset points only a single point lies outside the relative error of 5%. This clearly indicates that the swelling percentages obtained under this model as relatively closer to the experimental results from the linear dynamic swell meter.

Fig. 10
figure 10

Relative error yield by applied models while predicting swelling at different time intervals

Full size image

The overall error can be witnessed in Fig. 11, where errors from both the models are calculated for comparison. It can be claimed that the new model produces error somewhat half of the first order kinetics equation. The values of MAE, MSE and RMSE are calculated using the Eqs. (5) to (7). As a rule of thumb, minimum the values of these three error source higher will be the accuracy of the model. It can be recognized that the new model only produces a MAE value of 2.75% while, the existing model develops an error of 9.03%. This analysis clearly indicates that the curve extracted from the new model covers the swell meter results with less discrepancy.

Fig. 11
figure 11

Error comparison bar charts between two model

Full size image

Validation of the proposed model

In order to confirm the correctness of the new model, it was applied on Khadro formation results gathered from Khan et al. (2020). This formation exhibits a maximum swelling percentage of 5.7% after the recommended testing practice. The temperature under which the testing was done was equal to 32 °C. The clay content present in this formation was 26% (Khan et al. 2020).The goal is to validate the performance of the model on the other type of shale that comprises of different clay percentages, swelling and temperature. A total of 62 points were selected from the experimental data for the validation purpose. Table 3 shows the coefficient values for the adjustable parameters that were obtained after tuning the model. Again the model was divided into two separate regions for the higher accuracy. It can be seen that in both the regions the R2 is equal to or closer to 1. According to the definition, if the value of R2 is equal to 1 then it indicates a relatively higher accuracy of the fitting curve correlation.

Table 3 Coefficient of X and Y of the collapse equation for the Khadro formation
Full size table

Figure 12 shows the cross-plot for the validation of the model. It can be seen that the model is again validating a comparatively good performance for this formation. The swelling results obtain for this formation all falls around the perfect model line thus indicating the correctness of the proposed numerical model. The validation was further enhanced by the relative error plot as shown in Fig. 13. From this figure it is apparent that error lies within +25% making it a sound justification for the validation. Finally, to prove the efficiency of the model, Table 4 shows the values of different error sources. It can be observed that the model exhibits fairly small error percentages while predicting the swelling of the formation. This proves the accuracy of the proposed model in predicting the swelling of a shale formation.

Fig. 12
figure 12

Cross-plot for the validation of Khadro formation obtained by using proposed model

Full size image
Fig.13
figure 13

Relative error bar graphs for Khadro formation swelling obtained by using proposed model

Full size image
Table 4 Error % obtained from the implementation of proposed model on Khadro formation
Full size table

Swelling onset determination using proposed model for both datasets

The initiation of swelling for a shale formation is term as onset swelling point. This variable is denoted as ‘tc’ in Eq. (2). It is basically the contact time at which the swelling of shale formation commence when it comes directly in contact with a drilling fluid. Figure 14 shows the critical time for the initiation of swelling in Murree formation. The green point in the zoom view illustrating the experimental onset point of the swelling in this formation, whereas, for the proposed model it can be witnessed from the yellow point that the prediction of tc is closed to the experimental result. Similarly, in Fig. 15 again green and yellow points are showing the onset swelling time for both the experimental and predicted model, respectively. It can be observed that both points are again very close to one another. Table 5 shows the percentage deviation between the critical time for the swelling results. It is apparent from the result that in either of the two cases the deviation is less than 10%, which indicates a good performance by the proposed model.

Fig. 14
figure 14

Zoom view of the predicted swelling critical time for Murree formation

Full size image
Fig. 15
figure 15

Zoom view of the predicted swelling critical time of Khadro formation

Full size image
Table 5 Swelling critical time for both datasets
Full size table

Conclusion

Linear dynamic swell meter response was modeled successfully in this article. The formulation process of the model equation is a simple and direct and is basically dependent on the quantity of the clay content present in a shale sample, time of contact between the mud and the formation, response of experimental result and finally the temperature. Two disparate Pakistan’s shale formations obtained from two different regions were used for the development and validation of the model. It was observed that this proposed model is far better than conventional modeling techniques in modeling the response of the experimental results. The proposed model consists of tuning parameters. Integrity of these parameters depends upon the type of mud that is been in contact with the shale sample. Errors below 10% were obtained through the fine-tuning of these parameters that result in a better prediction of the swell meter experimental results. Moreover, it was envisioned that the information obtained from the equation helps in predicting the swelling initiation time when the mud and shale comes in direct contact with each other. This information is extremely helpful in forecasting and validating the swelling tendency of the shale sample in a particular mud.