Practical interpretation of pressure tests of hydraulically fractured vertical wells with finite-conductivity in naturally fractured oil and gas formations

Abstract

This paper presents a well test interpretation methodology using characteristic points and lines found on the pressure and pressure derivative versus time log–log plot for the characterization of a finite-conductivity fractured vertical hydrocarbon well in a double-porosity (heterogeneous) formation considering a new and practical analytical Laplacian model which require less computational time and have more accuracy than semi-analytical models. Some existing equations are found to work well for the new model, and new expressions are developed. The accuracy of the developed equations is successfully tested with synthetical examples.

Introduction

More than half of the world´s hydrocarbon reserves are stored in naturally fractured occurring formations which many times require hydraulic fracturing to enhance fluid production. These two issues: (1) naturally fractured reservoirs and (2) hydraulically fractured wells were originally separated from the well testing point of view. On one hand, the most classical paper on naturally fractured reservoirs was introduced by Warren and Root (1963) who presented a model to study the characteristic behavior of a porous medium possessing a network of fractures. They also introduce two key concepts: the interporosity flow parameter and the storativity ratio. On the other hand, Gringarten and Ramey (1973) made use of the Green´s function to introduce a mathematical model to describe the pressure behavior of a well with an infinite-conductivity fracture. This solution opened a new frontier in the field of well test analysis. Later, an excellent contribution to this field was made by Cinco-Ley et al. (1976). They provided an semi-analytical solution to study the pressure behavior of a vertical well intercepted by a finite-conductivity fracture. Besides, they also defined the onset value of the dimensionless fracture conductivity to establish whether a fracture falls into a finite-conductivity or infinite-conductivity classification.

Cinco-Ley and Meng (1988) built a bridge between fractured wells and naturally fractured formations by introducing a very practical Laplacian analytical solution to describe the pressure behavior of these combinate systems. This solution is also used in this work for comparison purposes. Several other important solutions have also been introduced, even including trilinear model. Finally, Wei et al. (2021) just introduced some very practical Laplacian solutions for finite-conductivity fractures which possess small differences with the solution provided Cinco-Ley and Meng (1988) and are worth of providing an interpretation technique which is the matter of this paper.

As it is well known, both transient rate and pressure analysis are important tools for reservoir characterization and adequate interpretation of those is also important for field appraisal and decision making. As commented by Escobar et al. (2018), there exists four ways of well pressure and rate data interpretation: (1) Type curve-matching, (2) Conventional straight-line, (3) Nonlinear regression analysis (computer assisted) and (4) TDS Technique. The last one can be found with detail in the books by Escobar (2015, 2019). This method uses characteristic points and lines found on the pressure derivative or reciprocal rate derivative versus time log–log plot from which analytical and direct-forward expressions are employed to find reservoir parameters. The very first paper on this technique was presented by Tiab (1993) for homogeneous infinite reservoirs, followed by Tiab (1994) for uniform-flux and infinite-conductivity hydraulic fractured wells and Tiab et al. (1999) for infinite-conductivity vertical fractured wells.

There are two noticeable differences between the pressure traces generated by the models of Wei et al. (2021) and Cinco-Ley and Meng (1988): (1) For dimensionless fracture conductivity (C_fD) less than 3, the first one does not display the classical trough during the transition period found on naturally fractured formations, and only bilinear flow is observed. For C_fD > 3, a bilinear flow regime is first observed then a trough interrupts the bilinear flow regime, but a bi-radial (elliptical) flow regime follows and, later, the radial flow regime is again interrupted by a trough. (2) The second model always has the trough during early bilinear flow regime, and another bilinear flow regime follows the trough. There is no trough during radial flow regime. Thereby, the objective of this work is to provide an interpretation technique for the model of Wei et al. (2021) applicable to both oil and gas wells (Appendix A). Some existing expressions presented by Engler and Tiab (1996), Tiab and Bettam (2007) and Escobar et al. (2015) were found to work here, and other were developed and successfully tested with synthetical and real examples.

Mathematical formulation

Wei et al. (2021) presented a novel and practical analytical well pressure solutions for finite-conductivity fractured wells in naturally occurring formations. This model considers the following assumptions: (1) The fracture in symmetrical around the wellbore and it possesses constant values of height, half-fracture length, width and permeability. (2) Fluid enters the wellbore only through the finite-conductivity fracture. (3) The matrix systems with a permeability, k_ma, porosity, ϕ_ma, and comprehensive compressibility, c_tma, bears a single and slightly compressible and constant viscosity fluid, µ. (3) the fracture network has a permeability, k_nf, porosity, ϕ_nf, comprehensive compressibility, c_tnf, has a single-phase fluid with viscosity, µ. (4) The fluid obeys Darcy’s law, negligible gravity and capillary force. The Warren-Root model is used to describe the naturally fractured system, then, natural fractures are assumed to be uniformly distributed. Reservoir properties over the entire domain are identical. Therefore, the reservoir is a homogeneous dual-porosity system with bulk permeability, k_fb. 5) The well produces at a constant rate.

Cinco-Ley and Meng (1988) presented a general semi-analytical solution for finite-conductivity fractured wells in dual-porosity reservoirs. They were also based on Warren-Root considerations which means that the physical model and assumptions are essentially the same. However, Wei et al. (2021) stated that semi-analytical or numerical solutions are the most used for pressure-transient analysis for finite-conductivity fractured wells in naturally fractured reservoir now. However, these just mentioned solutions are time-consuming and easily encounter some computation problems, such as accuracy, convergence and stability. The solution proposed by Wei et al. (2021) contains infinite series resulting in calculation times much shorter and simpler than the semi-analytical and numerical solutions presented in the literature, including the one presented by Cinco-Ley and Meng (1988).

The Laplacian infinite constant rate solution of Wei et al. (2021), which neglects wellbore storage effects, is given below:

$$\begin{gathered} \bar{P}_{D} (s) = \frac{\pi }{{s\sqrt {2C_{{fD}} } \sqrt[4]{{sf(s)}}\tanh \left[ {\sqrt {\frac{2}{{C_{{fD}} }}} \sqrt[4]{{sf(s)}}} \right]}} - \frac{\pi }{{2s\sqrt[{}]{{sf(s)}}}} + \hfill \\ \frac{{0.4063}}{{s\left( {C_{{fD}} + 0.8997 + \frac{{1.6252}}{\pi }sf(s)} \right)}} + \frac{1}{{2s}}\int\limits_{{ - 1}}^{1} {K_{0} \left( {\sqrt {(0.372 - \alpha )^{2} } \sqrt {sf(s)} } \right)d\alpha } \hfill \\ \end{gathered}$$

(1)

where f(s) is given by:

$$f(s) = \omega + \frac{{(1 - \omega )\lambda }}{{(1 - \omega )s + \lambda }}$$

(2)

The dimensionless fracture storativity ratio is given by

$$\omega _{f} = \frac{{(\phi c_{t} )_{f} }}{{(\phi c_{t} )_{{f + m}} }}$$

(3)

And the dimensionless matrix interporosity coefficient is:

$$\lambda = \alpha x_{f}^{2} \frac{{k_{{ma}} }}{{k_{{fb}} }}$$

(4)

Being α the shape parameter which depends upon the matrix surface area and block type. The dimensionless time, based on half-fracture length, is given below:

$$t_{{Dxf}} = \frac{{0.000263k_{{fb}} t}}{{(\phi c_{t} )_{{f + m}} \mu x_{f}^{2} }}$$

(5)

The dimensionless pressure and pressure derivative parameters for oil reservoirs are given by:

$$P_{D} = \frac{{k_{{fb}} h\Delta P}}{{141.2q\mu B}}$$

(6)

$$t_{D} *P_{D} ' = \frac{{k_{{fb}} h(t*\Delta P')}}{{141.2q\mu B}}$$

(7)

The dimensionless fracture conductivity introduced by Cinco-Ley et al. (1976) is defined as:

$$C_{{fD}} = \frac{{k_{f} w_{f} }}{{k_{{fb}} \;x_{f} }}$$

(8)

Pressure response

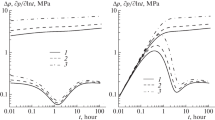
As observed in Fig. 1, there exist certain differences between the model of Wei et al. (2021) and the one presented by Cinco-Ley and Meng (1988). Although, substantially, both pressure behaviors are about the same, it is noticeable in the plot that the Cinco-Ley and Meng model presents bilinear flow regime before and after the characteristic transition displayed by naturally fractured reservoirs which consists of a trough. On the other hand, the model by Wei et al., matter of this study, presents bilinear flow regime before the trough but bi-radial or elliptical, Tiab (1994), flow regime after the trough. This flow regime is characterized by a 0.36-slope on the pressure derivative curve. However, referring to Figs. 2 and 3, the mentioned situation occurs when C_fD is greater than 3 (the plot shows for C_fD = 5). Below this value, the bilinear flow is not interrupted by the trough. It is also noticeable that the model of Wei et al. always displays a trough during radial flow regime, but the Cinco-Ley and Meng model does not has this characteristic.

Fig. 1

Dimensionless pressure and pressure derivative versus dimensionless time using the models of Wei et al. (2021) and Cinco-Ley and Meng (1988) when λ_m = 5 × 10^–4, C_fD = 20 and ω = 0.05

Fig. 2

Dimensionless pressure and pressure derivative versus dimensionless time for λ_m = 1 × 10–⁶ and different values of C_fD and ω

Fig. 3

Dimensionless pressure derivative versus dimensionless time for λ_m = 1 × 10^–6 and different values of C_fD and ω

The authors believe that the pressure response given by the model of Wei et al. (2021) is realistic since there is a trough for conductivity higher than 3 which indicates than the more conductive the fracture the more possibility of depleting the fluid inside the fracture, although partially; therefore, the final fracture network depletion takes place during the radial flow regime. The model by Cinco-Ley and Meng (1988) acts as if the fracture network feeding the hydraulic fracture were fully depleted before the radial flow regime shows up.

Figure 4 attempts to provide a better understanding of the system domain. The hydraulic fracture is fed by fracture network. Once they are depleted, the matrix feeds the fracture network and either bilinear, elliptical or radial flow follow that process.

Fig. 4

Schematic representation of the studied domain

Interpretation methodology

Some of the equations presented by Tiab and Bettam (2007) and Escobar et al. (2015) do not work in the model of Wei et al. (2021); therefore, some of the provided equations must be modified, and other new equations must be developed.

The interpretation methodology applied here follows the philosophy of the TDS Technique, Tiab (1993); therefore, unified pressure derivative behaviors should be obtained to develop analytical expressions for the determination of the reservoir parameters. Such is the case presented in Fig. 5 in which the early bilinear flow regime has a unified behavior which allowed us to obtain the pressure and pressure derivative governing equations which were also reported by Tiab and Bettam (2007):

$$P_{D} = \frac{{2.451}}{{\sqrt {C_{{fD}} } }}\left( {\frac{{t_{{Dxf}} }}{\omega }\,} \right)^{{1/4}}$$

(9)

$$t_{{Dxf}} *P_{D} ' = \frac{{0.6127}}{{\sqrt {C_{{fD}} } }}\left( {\frac{{t_{{Dxf}} }}{\omega }\,} \right)^{{1/4}}$$

(10)

Fig. 5

Unified dimensionless pressure and pressure derivative versus dimensionless time divided by ω during bilinear flow regime

As seen, the pressure behavior depends simultaneously upon both dimensionless fracture conductivity and dimensionless storativity ratio. Therefore, it was difficult to find a governing behavior during the trough since, at early time, the trough does not move neither to the right implying an independence from the interporosity flow parameter.

Solving for the fracture conductivity from Eqs. (9) and (10) led to:

$$k_{f} w_{f} = \frac{{1947.46}}{{\sqrt {\omega \mu (\phi c_{t} )_{{f + m}} k_{{fb}} t_{{BL}} } }}\left( {\frac{{q\mu B}}{{h(\Delta P)_{{BL}} }}} \right)^{2}$$

(11)

$$k_{f} w_{f} = \frac{{121.74}}{{\sqrt {\omega \mu (\phi c_{t} )_{{f + m}} k_{{fb}} t_{{BL}} } }}\left( {\frac{{q\mu B}}{{h(t*\Delta P)'_{{BL}} }}} \right)^{2}$$

(12)

When the pressure derivative is too noisy, it is recommended to draw the most representative line over the given flow regime and read the pressure derivative value at the time of 1 h. This also helps to have the best averaged value. Under this condition, Eqs. (11) and (12) became:

$$k_{f} w_{f} = \frac{{121.74}}{{\sqrt {\omega \mu (\phi c_{t} )_{{f + m}} k_{{fb}} } }}\left( {\frac{{q\mu B}}{{h(t*\Delta P)'_{{BL1}} }}} \right)^{2}$$

(13)

$$k_{f} w_{f} = \frac{{1947.46}}{{\sqrt {\omega \mu (\phi c_{t} )_{{f + m}} k_{{fb}} } }}\left( {\frac{{q\mu B}}{{h(\Delta P)_{{BL1}} }}} \right)^{2}$$

(14)

Another unified behavior was found in Fig. 6, this time, during bi-radial flow regime. However, the dimensionless pressure does not follow a parallel straight-line behavior along with the pressure derivative curve; so only a pressure derivative governing equation was developed for this flow regime, and it was also found that the developed expression coincided with the one reported by Escobar et al. (2015):

$$t_{{Dxf}} *P_{D} ' = \left( {\frac{{\pi t_{{Dxf}} }}{{26\xi }}\,} \right)^{{0.36}}$$

(15)

Fig. 6

Unified dimensionless pressure and pressure derivative versus dimensionless time divided by ω during bi-radial flow regime

It is worth to mention that the pressure behavior in Escobar et al. (2015) does go parallel to the pressure derivative curve, but it does not in the model of Wei et al. (2021).

Solving for the half-fracture length from Eq. (15), it yielded:

$$x_{f} = 5.4595\left( {\frac{{qB}}{{h(t*\Delta P')_{{BR}} }}} \right)^{{1.3889}} \sqrt {\frac{{t_{{BR}} }}{{\omega (\phi c_{t} )_{{f + m}} }}\left( {\frac{\mu }{{k_{{fb}} }}} \right)^{{1.778}} }$$

(16)

Again, sometimes it is better to read the value at the time of 1 h; then, Eq. (16) became:

$$x_{f} = 5.4595\left( {\frac{{qB}}{{h(t*\Delta P')_{{BR1}} }}} \right)^{{1.3889}} \sqrt {\frac{1}{{\omega (\phi c_{t} )_{{f + m}} }}\left( {\frac{\mu }{{k_{{fb}} }}} \right)^{{1.778}} }$$

(17)

Before going further, during the bi-radial flow regime the dimensionless fracture conductivity no longer affects this flow, but the dimensionless fracture storativity ratio does. As observed in the circled zone of Fig. 3, there exists a relationship between the bi-radial flow regime pressure derivative and the dimensionless fracture storativity ratios which was found to be:

$$\omega = \sqrt {0.3457 - 0.22982\ln \left( {\frac{{kh(t*\Delta P')_{{BR1}} }}{{141.2q\mu B}}} \right)}$$

(18)

Figure 7 shows the effect of the interporosity flow coefficient on the pressure test. Figure 8 displays a normalized behavior of the same case when both pressure and pressure derivative were multiplied by the interporosity flow coefficient. In this case, a unified unit-slope line and a minimum point are unique. They obey the following mathematical behavior:

$$t_{{Dxf}} *P_{D} ' = 0.4774\lambda t_{{Dxf}}$$

(19)

$$\lambda (t_{{Dxf}} )_{{\min }} = 0.026303$$

(20)

Fig. 7

Dimensionless pressure and pressure derivative versus dimensionless time for by ω = 0.005 and different λ_m values

Fig. 8

Unified dimensionless pressure and pressure derivative versus dimensionless time multiplied by λ_m for ω = 0.005 and different λ_m values

After plugging, the dimensionless time given by Eq. (5) into Eq. (19) yielded an expression for the estimation of the interporosity flow coefficient.

$$\lambda = \frac{{99.745\mu (\phi c_{t} )_{{f + m}} x_{f}^{2} }}{{k_{{fb}} t_{{\min }} }}$$

(21)

Replacement of the dimensionless time, Eq. (5), and dimensionless pressure derivative definition, Eq. (7), into Eq. (19) led to find another expression to calculate the interporosity flow coefficient using any arbitrary point during the unit-slope pseudosteady-state period during the transition period or trough:

$$\lambda = \frac{{(\phi c_{t} )_{{f + m}} x_{f}^{2} h(t*\Delta P')_{{us}} }}{{56.27qBt_{{us}} }}$$

(22)

Tiab (1993) established that during the radial flow regime, the dimensionless pressure derivative is governed by the following straight-line equation:

$$t_{D} *P_{D} ' = 0.5$$

(23)

The intersection between Eqs. (19) and (23) also led to find another expression to find the interporosity flow coefficient:

$$\lambda = \frac{{3971.71\phi \mu c_{t} x_{f}^{2} }}{{k_{{fb}} t_{{usi}} }}$$

(24)

Other expressions

The authors found that some expressions given by Engler and Tiab (1996), Tiab and Bettam (2007) and Escobar et al. (2015) can be used here changing the wellbore radius by the half-fracture length. The following equations also applied here:

$$\omega = {\text{0}}{\text{.15866}}\left\{ {\frac{{(t*\Delta P')_{{\min }} }}{{(t*\Delta P')_{r} }}} \right\} + {\text{ 0}}{\text{.54653}}\mathop {\left\{ {\frac{{(t*\Delta P')_{{\min }} }}{{(t*\Delta P')_{r} }}} \right\}}\nolimits^{2}$$

(25)

$$\omega = {\text{0}}{\text{.19211}}\left\{ {\frac{{{\text{5}}\mathop t\nolimits_{{min}} }}{{\mathop t\nolimits_{{b2}} }}} \right\} + {\text{0}}{\text{.80678}}\mathop {\left\{ {\frac{{5\mathop t\nolimits_{{min}} }}{{\mathop t\nolimits_{{b2}} }}} \right\}}\nolimits^{2}$$

(26)

$$\lambda = \left[ {\frac{{42.5h(\phi c_{t} )_{{f + m}} x_{f}^{2} }}{{qB_{o} }}} \right]\frac{{\left( {t*\Delta P'} \right)_{{\min }} }}{{t_{{\min }} }}$$

(27)

Tiab and Escobar (2003) also presented an equation for the determination of the interporosity flow coefficient from using the minimum point during the trough in the pressure derivative plot or the inflection point during the transition on the semilog plot.

$$\lambda = \frac{{3792\mu (\phi c_{t} )_{{f + m}} x_{f}^{2} }}{{k_{{fb}} t_{{\min }} }}\left[ {\omega \ln \left( {\frac{1}{\omega }} \right)} \right]$$

(28)

Engler and Tiab (1996) also presented expressions to find permeability and skin factor in naturally fractured formations:

$$k_{{fb}} = \frac{{162.2q\mu B}}{{h(t*\Delta P')_{{r1,r2}} }}$$

(29)

$$S = \frac{1}{2}\left[ {\mathop {\left( {\frac{{\Delta P}}{{t*\Delta P'}}} \right)}\nolimits_{{r{\text{1}}}} - \ln \left( {\frac{{k_{{fb}} t_{{r1}} }}{{(\phi c_{t} )_{{f + m}} \mu \mathop r\nolimits_{w}^{{\text{2}}} }}\frac{1}{\omega }} \right) + 7.43} \right]$$

(30)

$$S = \frac{1}{2}\left[ {\mathop {\left( {\frac{{\Delta P}}{{t*\Delta P'}}} \right)}\nolimits_{{r{\text{2}}}} - \ln \left( {\frac{{k_{{fb}} t_{{r2}} }}{{(\phi c_{t} )_{{f + m}} \mu \mathop r\nolimits_{w}^{{\text{2}}} }}} \right) + 7.43} \right]$$

(31)

Refer to Appendix A to find equations for gas wells.

Examples

Synthetic example 1

Synthetic test data were generated using data from the second column of table 1 and reported in Fig. 9. As observed in that plot, only bilinear flow is observed before the radial flow regime, and the transition period only interrupts the radial flow regime. From such plot, the following information was read:

$$\begin{aligned}& (t*\Delta P^{\prime})_{r} = 0.848124\,psi\quad t_{{\rm min}} = 2230\,h \\ &(t*\Delta P^{\prime} )_{{BL1}} = 22\,psi\quad (t*\Delta P^{\prime})_{{\rm min }} = 0.0442\,psi \\ &t_{b2} = \,203809.13\,h\quad (\Delta P)_{{BL1}} = 88\,psi\\ &t_{{usi}} = \,52000\,h\quad t_{{us}} = \,5877.92\,h \\ &(t*\Delta P^{\prime})_{{us}} = \,0.096\,psi \end{aligned}$$

Table 1 Input data for the example

Fig. 9

Pressure and pressure derivative versus time for synthetic example 1

Use Eq. (29) to find fracture network permeability:

$$k_{{fb}} = \frac{{{\text{70}}{\text{.6(120)(0}}{\text{.75)(1}}{\text{.34)}}}}{{(100)(0.848124)}} = 100.390\;{\text{md}}$$

The hydraulic fracture conductivity is found by using Eqs. (13) and (14):

$$\begin{gathered} k_{f} w_{f} = \frac{{121.74}}{{\sqrt {(0.01)(0.75)((0.18)(1 \times 10^{{ - 6}} )(100.390)} }} \hfill \\ \left( {\frac{{(120)(0.75)(1.34)}}{{(100)(22)}}} \right)^{2} = 995.670\;{\text{md - ft}} \hfill \\ \end{gathered}$$

$$\begin{gathered} k_{f} w_{f} = \frac{{1947.46}}{{\sqrt {(0.01)(0.75)((0.18)(1 \times 10^{{ - 6}} )(100.390)} }} \hfill \\ \left( {\frac{{(120)(0.75)(1.34)}}{{(100)(88)}}} \right)^{2} = 995.476\;{\text{md - f}}t \hfill \\ \end{gathered}$$

Use Eqs. (24), (27) and (28) to calculate the interporosity flow coefficient:

$$\lambda = \frac{{3971.71(0.75)((0.18)(1 \times 10^{{ - 6}} )(100^{2} )}}{{(100.390)(52000)}} = 1.027 \times 10^{{ - 6}}$$

$$\lambda = \left[ {\frac{{42.5(100)((0.18)(1 \times 10^{{ - 6}} )(100^{2} )}}{{(120)(1.34)}}} \right]\frac{{0.044198}}{{2230}} = 9.34 \times 10^{{ - 7}}$$

$$\begin{gathered} \lambda = \frac{{3792(0.75)(0.18)(1 \times 10^{{ - 6}} )(100^{2} )}}{{(100.390)(2230)}} \hfill \\ \left[ {(0.01)\ln \left( {\frac{1}{{0.01}}} \right)} \right] = 1.053 \times 10^{{ - 6}} \hfill \\ \end{gathered}$$

The dimensionless fracture storativity ratio with Eqs. (25) and (26).

$$\omega = {\text{15866}}\left\{ {\frac{{(0.044198)}}{{(0.848124)}}} \right\} + {\text{0}}{\text{.54653}}\mathop {\left\{ {\frac{{(0.044198)}}{{(0.848124)}}} \right\}}\nolimits^{2} = 0.0975$$

$$\omega = {\text{0}}{\text{.19211}}\left\{ {\frac{{{\text{5(2230)}}}}{{203809.13}}} \right\} + {\text{0}}{\text{.80678}}\mathop {\left\{ {\frac{{{\text{5(2230)}}}}{{203809.13}}} \right\}}\nolimits^{2} = 0.0129$$

Synthetic example 2

Pressure and pressure derivative versus time data reported in Fig. 10 were generated with the information provided in the third column of Table 1. It can be observed in this plot that there exists bilinear flow regime before the though and bi-radial flow regime after the trough. The following information was read from Fig. 10:

$$\begin{gathered} (t*\Delta P^{\prime} )_{r} = \,02.865\,psi~~~~t_{{\min }} = \,9471.83\,h \hfill \\ (t*\Delta P^{\prime})_{{BL1}} = \,2.13\,psi~~~~~~(t*\Delta P^{\prime} )_{{\min }} = \,0.536\,psi \hfill \\ t_{b2} = \,260875.69\,h~~~~~~~~(\Delta P)_{{BL1}} = \,8.5\,psi \hfill \\ t_{{usi}} = \,65000\,h~~~~~t_{{us}} = \,19789.45\,h \hfill \\ (t*\Delta P^{\prime})_{{us}} = \,0.7752\,psi~~~~(t*\Delta P^{\prime})_{{BR1}} = \,9\,psi \hfill \\ \end{gathered}$$

Fig. 10

Pressure and pressure derivative versus time for synthetic example 2

Fracture network permeability and hydraulic fracture conductivity were estimated with Eqs. (29), (13) and (14), respectively:

$$k_{{fb}} = \frac{{{\text{70}}{\text{.6(380)(3}}{\text{.2)(1}}{\text{.2)}}}}{{(120)(2.864)}} = 299.649\;{\text{md}}$$

$$\begin{gathered} k_{f} w_{f} = \frac{{121.74}}{{\sqrt {(0.05)(3.2)(0.1)(1.8 \times 10^{{ - 6}} )(299.649)} }} \hfill \\ \left( {\frac{{(380)(3.2)(1.2)}}{{(120)(2.130)}}} \right)^{2} = 1349846.5\;{\text{md - ft}} \hfill \\ \end{gathered}$$

$$\begin{gathered} k_{f} w_{f} = \frac{{1947.46}}{{\sqrt {(0.05)(3.2)((0.1)(1.8 \times 10^{{ - 6}} )(299.64)} }} \hfill \\ \left( {\frac{{(380)(3.2)(1.2)}}{{(120)(8.5)}}} \right)^{2} = 1355941.6\;{\text{md - ft}} \hfill \\ \end{gathered}$$

The half-fracture length was determined with Eq. (17) to be:

$$\begin{gathered} x_{f} = 5.4595\left( {\frac{{(380)(1.2)}}{{(120)(9)}}} \right)^{{1.3889}} \hfill \\ \sqrt {\frac{1}{{(0.05)(0.1)(1.9 \times 10^{{ - 6}} )}}\left( {\frac{{3.2}}{{300}}} \right)^{{1.778}} } = 306.805\;{\text{ft}} \hfill \\ \end{gathered}$$

The interporosity flow parameter was calculated using Eqs. (21), (22), (24), (27) and (28):

$$\lambda = \frac{{99.745(3.2)(0.1)(1.8 \times 10^{{ - 6}} )(300^{2} )}}{{300(9471.83)}} = 1.82 \times 10^{{ - 6}}$$

$$\lambda = \frac{{56.27(0.1)(1.8 \times 10^{{ - 6}} )(300^{2} )(120)(0.775)}}{{(380)(1.2)(19789.4447)}} = 9.39 \times 10^{{ - 6}}$$

$$\lambda = \frac{{3971.71(3.2)(0.1)(1.8 \times 10^{{ - 6}} ))(300^{2} )}}{{(299.649)(65000)}} = 1.057 \times 10^{{ - 5}}$$

$$\begin{gathered} \lambda = \left[ {\frac{{42.5(120)(0.1)(1.9 \times 10^{{ - 6}} ))(300^{2} )}}{{(3.2)(1.2)}}} \right] \hfill \\ \frac{{0.535}}{{9471.823}} = 1.025 \times 10^{{ - 5}} \hfill \\ \end{gathered}$$

$$\begin{gathered} \lambda = \frac{{3792(3.2)(0.1)(1.8 \times 10^{{ - 6}} )(300^{2} )}}{{(299.649)(9471.823)}} \hfill \\ \left[ {(0.05)\ln \left( {\frac{1}{{0.05}}} \right)} \right] = 1.037 \times 10^{{ - 5}} \hfill \\ \end{gathered}$$

Find the dimensionless fracture storativity ratio with Eqs. (25) and (26).

$$\omega = {\text{0}}{\text{.15866}}\left\{ {\frac{{0.535}}{{2.864}}} \right\} + {\text{0}}{\text{.54653}}\mathop {\left\{ {\frac{{0.535}}{{2.864}}} \right\}}\nolimits^{2} = 0.0487$$

$$\omega = {\text{0}}{\text{.19211}}\left\{ {\frac{{5(9471.82)}}{{260875.69}}} \right\} + {\text{0}}{\text{.80678}}\mathop {\left\{ {\frac{{5(9471.82)}}{{260875.69}}} \right\}}\nolimits^{2} = 0.0614$$

The dimensionless fracture storativity ratio can also be obtained from the elliptical flow regime by using the value of the pressure derivative at 1 h into Eq. (18):

$$\omega = \left[ {0.3457 - 0.22982\ln \left( {\frac{{(300)(120)(9)}}{{141.2(380)(3.2)(1.2)}}} \right)} \right]^{2} = 0.0584$$

Field example

Wei et al. (2021) presented a field example which was solved by their model and the model by Cinco-Ley and Meng (1988). Pressure and pressure derivative versus time data were digitized and reported in Fig. 11. Relevant information for this test is reported in the fourth column of Table 1.

Fig. 11

Pressure and pressure derivative versus time for field case

As observed in Fig. 11, pressure data are too noisy at early time, and bilinear flow regime is unidentified, but bi-radial flow regime can be seen between about 0.01 and 3 h. The following characteristic points were read from Fig. 11:

$$\begin{gathered} (t*\Delta P^{\prime})_{r} = \,89.67{\text{ psi}}\quad t_{{\min }} = \,69.3{\text{ h}} \hfill \\ (t*\Delta P^{\prime})_{{BR1}} = \,87{\text{ psi}}\quad (t*\Delta P^{\prime})_{{\min }} = \,46.6{\text{ psi}} \hfill \\ t_{b2} = \,69.3{\text{ h}} \hfill \\ \end{gathered}$$

Permeability was estimated with Eq. (29):

$$k_{{fb}} = \frac{{70.6(377)(2.242)(1.144)}}{{(65.62)(89.67)}} = 11.601\;{\text{md}}$$

Use the value of the pressure derivative during bi-radial flow at 1 h to find half-fracture length using Eq. (17) and the dimensionless fracture storativity ratio with Eq. (25):

$$\begin{gathered} x_{f} = 5.4595\left( {\frac{{(377)(1.144)}}{{(65.62)(87)}}} \right)^{{1.3889}} \hfill \\ \sqrt {\frac{1}{{(0.230)(0.1)(1.21 \times 10^{{ - 6}} )}}\left( {\frac{{2.242}}{{11.601}}} \right)^{{1.778}} } = 209.964\;{\text{ft}} \hfill \\ \end{gathered}$$

$$\omega = {\text{0}}{\text{.15866}}\left\{ {\frac{{46.6}}{{89.67}}} \right\} + {\text{0}}{\text{.54653}}\mathop {\left\{ {\frac{{46.6}}{{89.67}}} \right\}}\nolimits^{2} = 0.23$$

Find the interporosity flow parameter with Eq. (21):

$$\lambda = \frac{{99.745(0.1)(2.242)(1.21 \times 10^{{ - 6}} )(209.964^{2} )}}{{(11.601)(69.3)}} = 0.00148$$

Final comments

According to the obtained results from the worked examples, TDS Technique can reproduce the reservoir parameters in a practical and accurate way as seen from the examples of the given model for a finite-conductivity hydraulically fractured well in a heterogeneous (naturally fractured) formation.

In spite the data were digitized in the field example, Table 2 indicates that the results from the actual field case agree quite well with those from previous estimations by Wei et al. (2021) and Cinco-Ley and Meng (1988) who used either nonlinear regression analysis or type curve-matching since they mentioned the word matching and do not provide any analytical methodology.

Table 2 Comparison of field example results

The simulated examples results are summarized in Table 3. As it can be observed there, the reservoir parameters are estimated from several sources, and the results agree very well with the input data used for the simulations.

Table 3 Comparison of synthetic example results

Conclusions

New expressions for the characterization of well pressure tests are obtained for finite-conductivity fractured wells draining naturally fractured occurring formations for a model presented by Wei et al. (2021). Also, some existing equations were slightly modified to adjust to this model. The equations are successfully validated with synthetic and field examples.

The model of Cinco-Ley and Meng (1988) always presents the transition period caused by the fluid depletion inside the hydraulic fracture during the bilinear flow regime, also a bilinear flow regime follows once the transition period vanishes. The model by Wei et al. (2021) does not display transition period when the dimensionless fracture conductivity is less than 3. Above this value, a transition period interrupts the bilinear flow regime and bi-radial (elliptical) flow regime follows the transition, and another transition takes place during linear flow regime, meaning that the hydraulic fracture did not fully deplete the natural fracture network during the early time.

The first transition period does not allow to find reservoir parameters since it depends on both dimensionless fracture conductivity and dimensionless fracture storativity ratio. When, bi-radial flow dominates the pressure behavior, dimensionless fracture conductivity no longer affects the pressure behavior, and it is possible to find an expression to correlate between the dimensionless fracture storativity ratio and the value of the pressure derivative during this period which was extrapolated to its reading at 1 h.

Appendices

Appendix

Appendix A- Gas flow equations

The dimensionless time, pseudopressure and pseudopressure quantities are defined by:

$$t_{Dxf}=\frac{0.000263 k_{fb}t}{(\phi c_{t})_{f+m}\mu x_{f}^{t}}$$

(32)

$$m(P)_{D} = \frac{{hk[m(P_{i} ) - m(P)]}}{{1424.52q_{{sc}} T}}$$

(33)

$$t_{D} *m(P)_{D} ' = \frac{{hk[t*\Delta m(P)']}}{{1424.52q_{{sc}} T}}$$

(34)

Recently, Nguyen et al. (2020) remarked on the lacking of linearization due to the retaining pressure-dependent viscosity-compressibility in fracture wells in unconventional gas reservoirs. Such effect was also noticed by Escobar et al. (2012) who found some discrepancies when estimating the hydraulic fracture and naturally fracture parameters when using pseudotime and rigorous time.

To overcome the above issue, Agarwal (1979) introduced the pseudotime function to account for the time dependence of gas viscosity and total system compressibility:

$$t_{a} = \int\limits_{{to}}^{t} {\frac{{{\rm d}t}}{{\mu (t)c_{t} (t)}}}$$

(35)

Pseudotime is better defined as a function of pressure as a new function given in hr psi/cp:

$$t_{a} (P) = \int\limits_{{Po}}^{P} {\frac{{({\rm d}t/{\rm d}P)}}{{\mu (P)c_{t} (P)}}} {\rm d}P$$

(36)

Including the pseudotime function, t_a(P), in Eq. (32), the dimensionless pseudotime is given by:

$$t_{{Da}} = \left( {\frac{{0.0002637k}}{{\phi x_{f}^{2} }}} \right)t_{a} (P)$$

(37)

Notice that the viscosity-compressibility product is not seen in Eq. (37), since they are included in the pseudotime function. However, if we multiply and, then, divide by (μc_t)_i a similar equation to the general dimensionless time expression, Eq. (37), will be obtained.

$$t_{{Da}} = \left( {\frac{{0,0002637k}}{{\phi (\mu c_{t} )_{i} r_{w}^{2} }}} \right)\left\{ {[\mu (c_{t} )_{{f + m}} ]_{i} \times t_{a} (P)} \right\}$$

(38)

The equivalence of Eqs. (11) and (12) are:

$$k_{f} w_{f} = \frac{{197960.6}}{{\sqrt {\omega (\phi )_{{f + m}} k_{{fb}} t_{a} (P)_{{BL}} } }}\left( {\frac{{q_{{sc}} T}}{{h(\Delta P)_{{BL}} }}} \right)^{2}$$

(39)

$$k_{f} w_{f} = \frac{{12370.52}}{{\sqrt {\omega (\phi )_{{f + m}} k_{{fb}} t_{a} (P)_{{BL}} } }}\left( {\frac{{q_{{sc}} T}}{{h(t*\Delta P)'_{{BL}} }}} \right)^{2}$$

(40)

The equivalence to Eqs. (16) and (18) are:

$$x_{f} = 138.687\left( {\frac{{q_{{sc}} T}}{{h(t*\Delta m(P)'_{{BR}} }}} \right)^{{1.3889}} \sqrt {\frac{{t_{a} (P)_{{BR}} }}{{\omega (\phi )_{{f + m}} k^{{1.778}} }}}$$

(41)

$$\omega = \sqrt {0.3457 - 0.22982\ln \left( {\frac{{hk[t*\Delta m(P)']_{{BR1}} }}{{1424.52q_{{sc}} T}}} \right)}$$

(42)

The equivalence to Eq. (22) and (27) are:

$$\lambda = \frac{{(\phi )_{{f + m}} x_{f}^{2} h[t*\Delta m(P)']_{{us}} }}{{5.577q_{{sc}} Tt_{a} (P)_{{us}} }}$$

(43)

$$\lambda = \left[ {\frac{{4.218h(\phi )_{{f + m}} x_{f}^{2} }}{{qT}}} \right]\frac{{[t*\Delta m(P)']_{{\min }} }}{{t_{a} (P)_{{\min }} }}$$

(44)

The equivalence to Eqs. (29)-(31) are:

$$k = \frac{{711.26qT}}{{h\left[ {t*\Delta m(P)'} \right]_{r} }}$$

(45)

$$S' = 0.5\left[ {\frac{{[\Delta m(P)]_{{r1}} }}{{\left[ {t*\Delta m(P)'} \right]_{{r1}} }} - \ln \left( {\frac{{kt_{a} (P)_{{r1}} }}{{(\phi )_{{f + m}} r_{w}^{2} }}\frac{1}{\omega }} \right) + 7.4316} \right]$$

(46)

$$S' = 0.5\left[ {\frac{{[\Delta m(P)]_{{r2}} }}{{\left[ {t*\Delta m(P)'} \right]_{{r2}} }} - \ln \left( {\frac{{kt_{a} (P)_{{r2}} }}{{(\phi )_{{f + m}} r_{w}^{2} }}} \right) + 7.4316} \right]$$

(47)

Equations (21), (24), (25) (26) and (28) apply to gas reservoirs after dropping the viscosity-compressibility term and replace time by psudotime. Care must be taking when using Eq. (26) since a change for the pressure derivative by the pseudopressure derivative must be made.