Introduction

Both vegetable gum and synthetic polymer fracturing fluid systems use polymer solution as carrier. With its excellent rheological properties, the sand body is stably suspended in liquid state, and the proppant sand is brought to the designated position (Kruijf et al. 1993; Jin and Penny 1995; Holtsclaw et al. 2011; Malhotra and Sharma 2011; Lei and Clark 2007; Goel et al. 1998). The traditional evaluation method is to investigate the apparent viscosity of the fracturing fluid system, but whether there is a universal functional relationship between the apparent viscosity and the deposition rate of sand is always up in the air (Goel et al. 2000; Pellens et al. 2004). In the field application, the phenomenon of high apparent viscosity and weak sand suspension will also occur. In the past decade, hydrophobic associating polymers have been widely used (González et al. 2011; Lara-Ceniceros et al. 2007; Zhao et al. 2016). Such systems do not follow the Cox–Merz rule and cannot be evaluated only by apparent viscosity (Seiffert 2016; Oppong and Bruyn 2010; Caram et al. 2006; Vaccaro et al. 2000). Harris et al. (2009), Power et al. (2001) also investigated the rheological properties of natural vegetable gums and proposed that the viscosity and elasticity work together.

With the development of polymer condensed matter physics, DE Cloizeaux, DE Gennes and Edwards et al. conducted in-depth research on the motion mode of polymer chain and established relevant theoretical models (Ferry 1983; Doi and Edwards 1971; Gennes and P E 1985). The structure, entanglement and motion of polymer chains in solution are the sources of polymer solution singularity (Gotlib et al. 2009; Zhang et al. 2015; Brule and Hoogerbrugge 1995; Cho et al. 2017; Dušek and Prins 1969; Lipatov 1977). Polymer condensed matter physics introduces a series of mathematical concepts and theoretical models to describe the unique properties of polymers, including self-similarity, string drop chain model, instantaneous network theory (Annable et al. 1998; Tan et al. 2017), scale theory and so on.

In this paper, according to some existing theories, the change law of sand sedimentation rate and liquid property in the solution of commercial hydrophobic associating polymer and surfactant system was preliminarily investigated.

Materials and methods

Experimental materials

The hydrophobic associating polymer BCG-1 and anionic surfactant sodium dodecyl benzene sulfonate (SDBS) solution (The effective content of surfactant was 6%) were provided by Chengdu Baichun Petroleum Technology Co., Ltd. The water quality is tap water. The rheological properties of the liquid were determined by the Rheostess-6000 rheometer from Thermo Haake, Germany. The microstructure of the fluid was observed using the FEI Quanta 450 field emission environment scanning electron microscope from FEI corporation of America.

figure a

Sand settlement evaluation

The sedimentation rate of single sand is tested by custom sedimentation tube. The liquid to be tested is added into the inner cylinder, and the liquid level is 5 cm higher than the highest scale line. The ceramic granules with a diameter of 3.5 mm were placed in the internal cylinder, and the timing was started when the haydite was settled to the highest graduation line, and the timing was finished when the lowest graduation line was reached, the sedimentation rate of the sand was calculated and the average value was repeated five times.

Rheological evaluation

In order to further explore the influence factors of the sedimentation rate of sand, it is necessary for the rheological test of liquid. In order to ensure that the rheological test data can truly reflect the rheological characteristics of the solution, stress scanning experiments should be carried out on all samples before the test to determine the linear viscoelastic zone, so as to ensure that the samples are within the safe stress range in the later rheological test. The frequency of stress scanning experiment was set as 1 Hz, and the stress range was set as 0.1 ~ 10 Pa. After determining the safety stress value, the parameters such as the storage modulus (G′), the loss modulus (G″) and the phase angle (tan δ) of the sample are tested. The relationship between the loss modulus and the circular frequency can be obtained in the frequency scanning experiment to determine the relaxation time spectrum of the sample. The specific solution method of relaxation time spectrum is introduced below. The frequency range is set as 0.1 ~ 10 Hz, and the stress value is set as the safety stress value. The above experiments adopt HAAK RS6000-type rheometer; the use of the C60/1° Ti vertebral plate-type rotor is tested. The apparent viscosity (η) was measured with a six-speed viscosity meter.

Relaxation time spectrum

The concept of relaxation time is introduced when discussing the constitutive equation of viscoelastic fluid. Relaxation time is the ratio of the characteristic constant viscosity to the modulus of the material, and it is a function of the contribution of each relaxation mode to the overall performance of the polymer. Studying the change of relaxation time spectrum can better understand the law of fluid viscoelastic change (Ramkumar et al. 2015; Kontou 1998; Gotlib et al. 2003).

In the integral Maxwell constitutive equation generalized by the Bolzmann superposition principle, a memory function is introduced to characterize the influence of the stress of the material in the past time period (t-t′) on the present moment. The integral form:

$$ m\left( {t - t^{\prime}} \right) = \mathop \smallint \limits_{0}^{\infty } ~\frac{{H\left( \lambda \right)}}{\lambda }e^{{ - \frac{{t - t'}}{\lambda }}} ~d\lambda $$
(1)

The memory function is actually the sum of the storage modulus of the different motor patterns, The H(λ) is the relaxation spectral function, and the H(λ) dλ is the constant characteristic viscosity of all the motion patterns. The relaxation time spectrum is the image of the H(λ)-λ relation.

The formula proposed by Ferry (1983) for the relaxation time spectrum H(λ) approximate solution by dynamic loss modulus is:

$$ H\left( \lambda \right) = \frac{2}{\pi }\left[ {G^{\prime\prime}\left( \omega \right) - \frac{{dG''\left( \omega \right)}}{{d\ln \omega }}} \right]_{{\frac{{\sqrt 3 }}{\omega } = \lambda }} $$
(2)

Results and discussion

Model

When dealing with concentrated polymer solution, due to the aggregation state of polymer skeleton and micelle, Doi–Edwards pipe motion model and DE Gennes’ molecular chain creep model can be introduced according to the research method of dense system (Doi and Edwards 1971; Gennes and P E 1985). In the pipe model (Fig. 1), a polymer chain moves in a tube of other high polymer chains, and the polymer’s entangled form is the entanglement of the polymer tube and tube. The patterns of motion of the chains are divided into two types. The first is the entropy elastic deformation that keeps the topological structure of polymer entanglement unchanged, and the process is divided into the stretching and compression of polymer chain. These two kinds of motions will lead to the trend of restoring the equilibrium configuration of polymer chain, and the relaxation process requires less time. The second is the long-range motion of the polymer chain that changes the topological structure, after the movement of the molecular chains reaches a certain level, and the relative positional relationship of the polymer tubes is varied, and this relaxation process has higher relaxation time. It is also the process of the polymer chain untangling and forming a new entangled structure.

Fig. 1
figure 1

Polymer chain bead spring model; a equilibrium configuration of polymer chain. b compression conformation of polymer elastic deformation. c stretch conformation of polymer chain with elastic deformation. d topological deformation of polymer chains

Full size image

In order to simplify the model, the bead spring model is used in Fig. 1 to replace the DE Gennes beads-on-string chain model, but the scale parameters of the DE Gennes model about thermal correlation, exclusion volume and long-range shielding effect are still retained. The elasticity of the spring depends on how far the polymer chain goes off equilibrium configuration. The length of the spring ξ, which is determined by that upper limit of the excluded volume effect of the polymer chain, is the minimum movement distance that remains constant for the polymer entanglement structure. The diameter ξT of the small ball is determined by the fluctuation dissipation theorem, which is the lower limit of the scale of the polymer chain to produce the excluded volume effect. This model is only an equivalent replacement model.

After combining the DE Gennes model with the Doi–Edwards model, we first proposed a simplified model of the tertiary structure of the polymer solution. As shown in Fig. 2, the structure of polymer solution can be divided into three levels: (a) condensed matter structure, (b) pipe structure and (c) bead spring structure. They represent macromolecular condensed matter, long-range structure and short-range structure, respectively.

Fig. 2
figure 2

BCG-1 solution tertiary structure; a micelle + skeleton structure, b pipe structure and c bead spring structure

Full size image

Better condensed matter structure can make the force distributed evenly and enhance the resistance of the solution to external forces. Remote action can strengthen the links between chains, such as entanglement, cross-linking and hydrophobic association, and can increase the mechanical properties of the system. The short-range effect is mainly reflected in the conformation of the polymer chain, The extended polymer chains become more prone to entanglement, while the polymer chain with hydrophobic structure can enhance the remote structure, but at the same time, it will produce the internal association of the polymer chain, making the polymer chain curl. The addition of surfactants can promote the transition from intramolecular association to intermolecular association, thus improving the structural strength.

Effect of polymer concentration

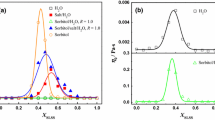
Prepare BCG-1 solution (concentration range 0.1–0.5%) with tap water. Figure 3 shows the relationship between the deposition rate (SR) of sand in thickener solutions of different concentrations and its storage modulus (G′), loss modulus (G″) and apparent viscosity (vertical). Table 1 shows the correlation coefficients of SR with G′, G″ and tan δ.

Fig. 3
figure 3

The change curve of ceramsite sedimentation rate (SR), storage modulus (G′), loss modulus (G″) and apparent viscosity (η) when BCG-1 concentration is increased

Full size image
Table 1 Calculation results of correlation coefficient between storage modulus (G′), loss modulus (G″), apparent viscosity (η), phase angle (tan δ) and ceramsite sedimentation rate (SR)
Full size table

It can be seen from the data in Fig. 3 and Table 1 that all the properties of the BCG-1 solution increase significantly with the increase in the concentration, and the performance of all aspects of the liquid seems to be related to the sedimentation rate of the sand. The above data only show that the ability of the system to resist the gravity of sand has increased, but it is impossible to correlate one of the properties of the solution with the settling rate of sand alone.

Next, the mechanical structure of the system is analyzed by means of scanning electron microscopy photographs of BCG-1 solution. Figure 5a shows the condensed structure of polymer chains in BCG-1 pure solution. The whole system presents a combination of polymer micelles and polymer skeleton. Under the action of external force, the polymer micelles tend to produce overall movement, resulting in an increase in solution structural instability. At the same time, the overall movement of the polymer micelles consumes most of the external force and cannot exert the resistance effect caused by the movement of the polymer chain inside the polymer cluster.

Figure 5b shows the state of attachment between these micelles, with a large number of polymer clusters linked by a polymer backbone and partially filamentous. It is obvious that the overall movement of the polymer micelles must overcome the binding force of some of the skeletons, and the polymer chain in the polymer skeleton is much less than the micelles, which will result in a more concentrated stress on the polymer chains in the polymer skeleton. Under this concentrated stress, the polymer chains in the skeleton will produce various motions. At this time, the long-distance interaction between the polymer chains begins to hinder the movement of the polymer chains and macroscopically shows the resistance of the skeleton when it is stretched and moved. On the other hand, the polymer chain in the bead spring model is an elastic polymer chain. When an external force acts, a part of the external force will be converted into an elastic stress inside the molecule. The performance of the polymer skeleton essentially depends on the force between the polymer chains.

In conclusion, for the micelle skeleton structure of BCG-1 pure solution, the key to its mechanical properties lies in the strength of the polymer skeleton. When the polymer concentration increases, the polymer chain density of the whole system increases, the polymer chain entanglement structure in the skeleton becomes more complex, and the hydrophobic chain segments increase, and the remote acting force also increases. The reaction force of sand is increasing, so the sedimentation rate of sand decreases gradually.

Effect of surfactant concentration

In order to further study the sand sedimentation rate (SR) affected by the polymer network structure, we used 0.4% BCG-1 solution to carry out sand sedimentation experiments at different SDBS concentrations. Then, the microstructure and rheological data of each liquid were analyzed. Figure 3 shows the relationship between the properties of the solution and the rate of sand settling after the addition of SDBS. Since the pure polymer system differs greatly from the nature of the compound system, we present its data separately in Table 2.

Table 2 B-55 added amount of ceramsite sedimentation rate (SR), the storage modulus (G′), the loss modulus (G″), the influence of the apparent viscosity (eta)
Full size table

From Table 2, we can see that the sand sedimentation rate in the compound system is significantly lower than that of the pure polymer solution. With the addition of 0.05% SDBS, the sand sedimentation rate has been reduced to one-fifth of that of the pure polymer solution, and G′ has decreased slightly.

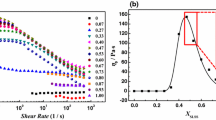
In Fig. 4, when the concentration of SDBS is 0.05–0.20%, G′ increases slowly, G″ remains basically unchanged and η shows a stable trend. The macroscopic properties of the liquid did not change much, but the rate of sand sedimentation declined steadily. When the concentration of SDBS exceeds 0.25%, the performance of the liquid increases greatly, and the sand sedimentation rate still keeps decreasing. The data in Table 3 show that the sand settling rate is highly correlated with phase angle (tan δ), and tan δ is the ratio of liquid G′–G″. The description only considers that a certain factor cannot comprehensively reflect the change of the sand sedimentation rate, and it is necessary to conduct a comprehensive investigation of the liquid properties. Based on the above experimental data, in order to investigate how the effect of SDBS on liquid properties is carried out, the macroscopic viscoelastic properties and microstructure of the liquid are analyzed separately.

Fig. 4
figure 4

B-55 added amount of ceramsite sedimentation rate (SR), the storage modulus (G′), the loss modulus (G″), the influence of the apparent viscosity (eta). (0.4% BCG-1 solution)

Full size image
Table 3 Increase amounts of SDBS, storage modulus (G′), loss modulus (G″), apparent viscosity (eta), phase Angle (tan δ) and correlation coefficient for that sedimentation rate (SR) of the haydite (0.4% BCG-1 solution)
Full size table

In the analysis of Fig. 4, we found that there was a sudden change in the solution property curve at the concentration of surfactant of 0.25%. In order to further verify this phenomenon, we combined the frequency scanning data of the liquid to conduct rheological analysis on the fluid at different phases. The following are the frequency scan data of G′, G″, and tan δ of different concentrations of SDBS compound system.

Figure 5c shows that when the amount of SDBS is 0.1%, the structure of the system is similar to that of the pure BCG-1 solution, it is still dominated by micelles, and the system does not change much. Figure 5e shows that when the SDBS is added at 0.2%, the connection between the micelles is significantly enhanced, but the morphology of the micelle skeleton structure can still be seen. Comparing the electron micrographs of SDBS concentrations of 0, 0.1% and 0.2% (Fig. 5b, d, f), it was found that the above three groups of samples did not appear too different in detail. And Fig. 4 shows that when the SDBS concentration is within this range, the properties of the system do not change appreciably, so the change in the sedimentation rate of the ceramic particles at this phase can only be attributed to fine adjustment of the architecture, and to the effect that the internal forces of the framework may be enhanced. Figure 5g shows that when the concentration of SDBS reaches 0.35%, the linkage between the polymer clusters is so tight that some of the parts are already integrated. Figure 5h shows that the strength of the skeleton has been greatly improved. In fact, the structure at this time has made a big difference from the skeleton micelle structure. It is even impossible to call the skeleton. The interaction between the polymer chains is greatly increased, ending the state in which the micelles are independent of each other. This tight structure not only provides a stronger binding force that allows the external force to be immediately transferred around, but also the strong polymer skeleton enables a considerable part of the external force to be converted into the elastic deformation of the polymer chain, which is also the reason for the sharp increase in G′. As shown in Fig. 4, the overall system’s ability to resist external forces also increases, and the sand sedimentation rate is extremely low.

Fig. 5
figure 5

Environmental scanning electron micrograph a, b 0.4% BCG-1 aqueous solution, c d 0.4% BCG-1 aqueous solution added 0.1% SDBS, e f 0.4% BCG-1 aqueous solution added 0.2% SDBS, g, h 0.4% BCG-1 aqueous solution added 0.35% SDBS

Full size image

In Fig. 6, the storage modulus (G′), loss modulus (G″), and phase angle (tan δ) all produce step change information, which is consistent with the boundary point of the above experimental data. According to the above information, the concentration of SDBS can be divided into three phases of I, II, III according to the boundary points of 0.05% and 0.20%. Analysis of the phase angle curve Fig. 6c shows that the process of transferring from the phase I to the phase II is a process of mutation. The transition from the phase II to the phase III is carried out step by step, and it can be divided into a gradual decrease in the phase angle of the long relaxation time zone and a sudden change in the low relaxation time zone. Therefore, it is possible to focus on the long relaxation time zone of the phase II.

Fig. 6
figure 6

Curve of liquid properties with relaxation time in SDBS systems with different concentrations (0.4% BCG-1 solution). a storage modulus (G′), b loss modulus (G″), c phase angle (tan δ)

Full size image

Since the test of the rheological data in Fig. 4 is carried out at a relaxation time of 0.2 s–0.3 s, when we analyze Fig. 6a and Fig. 6b, we focus on this phase. It was found that in this relaxed region, as the concentration of SDBS increased, the G″ curve showed a small change and showed a tendency to decrease first and then increased, while the G′ curve gradually increased. In the phase III, both G′ and G″ increase with the increase in the concentration of SDBS, and the growth of G′ is much larger than G″, which is also the cause of the sudden change in the phase angle curve.

Taken together, the rheological data verified that the concentration of SDBS had a phased effect on the system. When the concentration of SDBS is between 0.05 and 0.20%, the rheological properties of the system show slight changes, but during this phase, the sand sedimentation rate is greatly reduced. Continue to investigate the relaxation time spectrum of the material to determine the effect of the polymer chain’s motion pattern on the overall system.

Before analyzing the relaxation time spectrum, the polymer motion patterns are first divided. According to the above-mentioned three-level structure model, the following assumptions are made: 1. The skeleton is the main force unit and the polymer motion mode in the skeleton is creeping and elastic stretching. 2. The motion in the micelle is mainly based on peristalsis. Under this assumption, the relaxation time spectrum is analyzed.

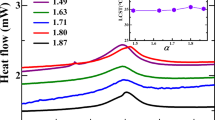
Figure 7a shows the change of the relaxation time spectrum with the concentration of SDBS. It can be clearly seen that when the concentration of SDBS is 0.15%, the relaxation time spectrum shows a minimum value in the long-term region. The brown region of the relaxation time spectrum in Fig. 7b indicates that there is less long relaxation motion and the long relaxation motion is of secondary importance throughout the system. At the same time, the elastic movement of short relaxation time has shown an increasing trend. And this trend is ubiquitous in the phase II, indicating that the polymer chain movement form at this phase is a process in which the creep of the polymer chain is reduced and the elastic motion is increased. The condensed state structure of the reaction on the electron microscopic images has not changed greatly, which indicates that the main factors causing the change of system properties are short-range structure and long-range structure. The reason for this change may be that the SDBS molecule binds to the hydrophobic segment in the polymer segment, thereby reducing the binding force inside the polymer chain and tending to stretch the polymer conformation. The entanglement between the stretched polymer chains is more tight, which increases the resistance of the polymer’s long relaxation motion and change the action of external force into the elastic motion of polymer chain. Due to the low effective amount of surfactant in SDBS, this phenomenon appears only as a low-amplitude change in macroscopic view.

Fig. 7
figure 7

a Relaxation time spectrum at different concentrations of SDBS, b top view of relaxation time spectrum

Full size image

Based on the comprehensive rheological data, electron micrograph and relaxation time spectrum, we propose a three-phase model of surfactant action and combine the three-level structure model to explain the different phases.

The phase I of pure polymer is micelle skeleton model, as already mentioned in the previous section. Early in the phase II, the addition of SDBS makes the system property mutate compared with the phase I, and the surfactant molecule increases the effect of the interaction between macromolecules, which is the change process of the near structure enhancement. Later in the phase II, the concentration of SDBS continued to increase, the micelle skeleton structure began to change, the polymer chain in the micelle transferred to the skeleton, and the system’s resistance to external forces began to increase. This process was mainly the change of the remote structure and the condensed matter structure, but the change was too small, and the macroscopic properties did not show obvious performance. In the phase III, the characteristics of the system are greatly increased, the movement of the polymer chain in each relaxation time is increased, the elastic motion is increased and is transferred to a lower relaxation time, and the decrease in the sedimentation rate is the result of the structure enhancement of the various levels, which is also a process of greatly changing the structure of the various levels.

Conclusions

The effects of polymer concentration and surfactant concentration on the properties of the solution, as well as the relationship between the rate of sand settling and various properties, were investigated. A three-stage structure of hydrophobically associating polymer solution was proposed, and a three-stage model of the interaction between polymer and surfactant was established, and it was found that with the increase in SDBS concentration, the properties of the solution changed in phases. When the concentration of SDBS was 0.05–0.2%, the rheological property of the system changed slightly with the change of SDBS concentration, while the deposition rate of sand decreased significantly. The analysis of microstructure and rheological data showed that the phase was dominated by the transformation of polymer movement mode. When the concentration of SDBS exceeds 0.2%, the properties of the system increase significantly with the increase in SDBS concentration. In addition, no matter at which phase, the deposition rate of sand is highly correlated with the change trend of phase angle, indicating that elasticity and viscosity have the same important influence on the performance of liquid suspended sand, while the evaluation of apparent viscosity on liquid is not accurate. Phase angle reflects the change of molecular chain motion mode. Therefore, phase angle is a more effective index for evaluating sand carrying performance of hydrophobic association fracturing fluid.