Abstract
Suites of wireline well logs and three-dimensional (3D) seismic data were integrated to characterise the reservoir and estimate the hydrocarbon in Otigwe field, coastal swamp depositional belt, Niger Delta. The 3D seismic data were used to generate seismic sections through which fourteen faults and two horizons of interest were mapped across four wells. Depth structural map generated from the mapped faults and horizons of interest shows that the trapping mechanism within the field is fault-supported anticlinal structural trap. The four available wells were correlated using lithostratigraphic correlation to establish two reservoir continuities (Reservoir A and B). The estimated reservoir fluid volume at surface condition using reservoir simulation and modelling software is 59 MMstb for reservoir A and 25.70 MMstb for reservoir B. On the other hand, the estimated reservoir fluid volume at surface condition using analytical method is 52.58 MMstb for reservoir A and 18.85 MMstb for reservoir B. Using reservoir simulation and modelling software, the average net-to-gross ratio and shale volume for reservoir A range from 0.86 to 0.89 and 0.11 to 0.14, respectively, while for reservoir B the range is between 0.69 to 0.82 and 0.18 to 0.31, respectively. On the flipside using the analytical method, the average net-to-gross ratio and shale volume for reservoir A is 0.78 and 0.22, respectively. The results from the volumetric estimation of reservoir fluids showed close values using both methods and reservoir A is more prolific compare to B.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The Niger Delta Basin is ranked as one of the most prolific deltaic systems in the world with respect to hydrocarbon accumulations or reserves. This hydrocarbon province contains only one petroleum system called the Akata-Agbada petroleum system (Tuttle et al. 1999). It is regarded as the most significant region within the West African Continental Margin (Aizebeokhai and Olayinka 2011). Hydrocarbons (oil and gas) in the Niger Delta are mostly extracted from the Agbada Formation which is predominantly made up of unconsolidated sandstone and shale. Since one of the ultimate goals of the oil and gas industry is to identify and characterise the reservoirs and estimate the volume of oil and gas in place, accurate delineation of structural traps on 3D seismic sections and effective well log analysis is required. The application of well logs and 3D seismic for the characterisation and hydrocarbon volume estimation will aid in the decision-making process by identifying commercially viable zones for exploitation.
Well log analysis and 3D seismic survey are two essential techniques used for reservoir characterisation in the petroleum industry. These techniques help the geoscientist to have a better knowledge of the physical properties and structural setting of the reservoir rock and the fluid contents. According to Weber (2012), when well log analysis is integrated with 3D seismic interpretation, a detailed view of the subsurface geology and geophysical properties can be established. Since well logs are in depth, the top and base of reservoirs can be mapped out and used to construct a subsurface structural and isopach/isobath map (Weber 2012). Depth measurement from well logs can be used to convert two-way-time on a seismic section to depth. Reservoir fluid contents can be analysed through the use of well logs. Hence, fluid saturation within the porous media can be calculated analytically using Archie’s formula, for clean sandstone formation. According to Ajisafe and Ako (2013), it is more advantageous to integrate well log and seismic data for reservoir characterization than to use well data alone, because seismic data enables the extrapolation and interpolation beyond and between sparse well controls. The vertical resolution obtained from well log data is excellent but has a poor areal resolution. On the other hand, 3D seismic data provide high areal resolution, but with poor vertical resolution (Ajisafe and Ako 2013). Accuracy of subsurface structural mapping and analysis would be significantly enhanced by integrating well logs and seismic data (Adejobi and Olayinka 1997; Barde et al. 2002).
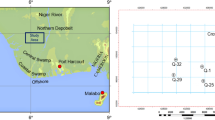
Otigwe Field is located in the coastal swamp depositional belt (depobelt) within the Niger Delta oil province, as shown in the red oval (Fig. 1).
Geological setting
The Niger Delta is located in the Gulf of Guinea, on the West Africa Margin and spreads all through the Niger Delta province between longitude 5 °E to 8 °E and 4 °N to 6 °N (Tuttle et al. 1999) (Fig. 2). The Niger Delta Basin has three formations which are the marine Akata, paralic Agbada and continental Benin Formations (Table 1). The Akata Formation is the primary source rock and is made up of marine shale (Doust and Omatsola 1990). The reservoir rock of the Agbada Formation is made up of sandstone with shale intercalation. According to Kulke (1995), during the formation of the delta, there was equilibrium between the rate of subsidence and sedimentation. The depositional pattern of the sediment was influenced by the tectonic setting and structural configuration of the terrain. The delta has prograded south-westwards from the Eocene to Recent forming five depositional belts at each stage of the formation (Doust and Omatsola 1990).
a Rollover structures with clay filled channel b Structure with multiple growth faults c Structure with antithetic faults and d collapsed crest structures (Tuttle et al. 1999)
Rollover structures, multiple growth faults, antithetic faults and collapsed crest structures are the main structural features found in the Niger Delta (Fig. 2) (Tuttle et al. 1999). According to Evamy et al. (1978) and Stacher (1995), structural traps were formed during synsedimentary deformation of the petroleum bearing Agbada paralic sequence. The structures become more complex towards the south with respect to gravitational instability of the under compacted, over pressured Akata Formation (Tuttle et al. 1999). According to Doust (1989) hydrocarbons are trapped within the growth fault structure and about 4 billion cubic metre are present in existing field. The seal rock in the Niger Delta is primarily interbedded marine shales within the Agbada formation. Three types of seals are available: smearing of clay along faults, vertical seals and interbedded sealing layers against which subsurface reservoir sands juxtapose because of faulting (Doust and Omatsola 1990).
Data set and methodology
The data set consists of 3D seismic data (SEG-Y format), well logs from four wells, well header, well deviation from the four well and check shot (Time-Depth data). Two methods of data analysis were employed in this study. These are the reservoir simulation/modelling software and analytical method which involves using appropriate analytical formulae Fig. 6.
Reservoir simulation and modelling software was used in this study. The 3D seismic and well data set were imported into the software. The wells are shown in the seismic survey base map (Fig. 3). Non-reservoir zones, tops and base of the reservoirs were delineated from the well logs (using gamma, density, sonic logs, etc.) and correlation of the reservoir top and base were established. The reservoir simulation and modelling software converted the 3D seismic data to series of seismic sections consisting of inlines and crosslines, through which picking of major and minor fault were carried out and interpreted using the appropriate tools on the menu bar. This conversion process enables the identification of the horizon of interest (top of reservoir), which allow the picking of the horizons throughout all the inlines and crossline on the seismic sections. Check shot (time-depth chart) data for well 2 were used to convert reservoir tops from the well log in depth domain to two-way time domain on the seismic sections (Fig. 4). These logs were also used to produce and display synthetic seismograms on the 3D seismic section for picking of horizons. The top of the horizons of interest which represents the reservoir top was adequately mapped and interpreted. The time and depth structural maps were produced to identify the area that was covered with hydrocarbon. The area was integrated with the thickness of the reservoir for the evaluation and estimation of the bulk volume of hydrocarbon. The flow chart in Fig. 5 and Fig. 6 clearly illustrates the steps of the methodology.
Shale contents are mostly present within the hydrocarbon-bearing sandstone reservoir. The presence of shale in the productive zone has severe impact on the petrophysical properties and can cause a reduction in the effective and total porosity, as well as permeability. Moreover, it also poses problem in the interpretation of wireline well logs and can affect proper and effective estimation of hydrocarbon or STOOIP (Moradi et al. 2016). Hence, its determination is crucial in solving the problem stated earlier. According to Szabo (2011), various methods exist for shale volume estimation, such as gamma ray log, spontaneous potential log or porosity-neutron log. In this study, gamma ray log technique was used for the shale volume estimation by first estimating the gamma ray index (IGR) (Eq. 1).
where: GRlog represents gamma ray reading at the depth of interest, GRmin and GRmax represent minimum and maximum gamma ray values of the clean and shale formation, respectively (Szabo 2011).
Secondly, to obtain the realistic shale volume estimation without overestimating the content of shale (first-order approximation: Vsh = IGR), a nonlinear relationship (for unconsolidated rock or chemically immature rock) was used in this study, by employing Eq. 2 (Szabo 2011). Since the Niger Delta sedimentary sequences are Tertiary rock or younger rock, Eq. 2 was used.
Determination of total porosity
Application of neutron-density log in porosity determination is the most commonly used technique in reservoir rock penetrated by a well (Ijasan, Torres-Verdin and Preeg 2013). The total porosity in hydrocarbon-bearing formation can be determined using Eq. 3 (Gaymard and Poupon 1968 cited in Ijasan, Torres-Verdin and Preeg 2013).
For sandstone lithology, \(\rho _{{ma}} = \frac{{2.65\;{\text{g}}}}{{{\text{cm}}^{2} }}~,~\rho _{b} ~{\text{is~obtained~from~density}}\;{\text{logand}}~\)
Determination of effective porosity
A porosity model and equation proposed for shaly-sand reservoirs by Al-Ruwaili (2007) were used for the determination of the effective porosity (Eq. 4). This was employed because the lithological facies in the Niger Delta reservoirs is made up of shaly-sand sequences.
Archie’s formula for water saturation determination
Archie’s formula is the basic or elementary formula for computing water saturation for both the virgin and invaded zones in the primary life of a given reservoir (Al-Awad 2001). For a reservoir, the exactness or accuracy of the water saturation value depends on the exactness of the Archie’s parameters (a, m and n). In this work, Archie’s equation was used in the determination of the water saturation in the virgin zone (without mud filtrates) (Eq. 5).
where Sw represents water saturation level, Rw is the water resistivity, Rt is the formation resistivity (virgin zone) containing the hydrocarbon, ∅ the total porosity of the reservoir.
Archie’s parameters a, m and n represent: tortuosity factor, cementation factor and saturation exponent.
SW = Formation water saturation (fraction; obtained from log data).
So = oil saturation.
Determination of Net-To-Gross Ratio
The net-to-gross ratio is the ratio of the total thickness of the subsurface productive pay zone to that of the total thickness of the subsurface reservoir interval for a vertical well. Also, the net-to-gross ratio has a direct relationship with the volume of shale as shown in Eq. 7 (Abbaszadeh et al. 2003). When an entire reservoir interval is a pay zone, then net-to-gross is equal 1.0. Since the four available wells in this study are all vertical wells and the entire sandstone reservoir or hydrocarbon-bearing interval contains intercalation of shaly-layer, the net-to-gross ratio will therefore be less than unity (i.e. 1.0) and Eq. 7 was used for the computation.
Permeability determination
Permeability is the ability of a porous medium to transmit fluid. In this study, the empirical expression for permeability estimation by Awolabi, LongJohn and Ajienka (1994) was employed. This method was used because it considers the unconsolidated reservoir sand within the Niger Delta hydrocarbon province. The mathematical expression involves the relationship between effective porosity, permeability and irreducible water saturation as shown in Eq. (8).
Volumetric estimation technique
The hydrocarbon volumes were estimated using the volumetric method (Eqs. 9, 10 and 11). Firstly, the hydrocarbon pore volume was calculated using the reservoir simulation and modelling software prior to the computation of the original oil in place at surface condition by means of the formation volume factor. The petrophysical parameters such as porosity and water saturation, as well as net-to-gross ratio and reservoir thickness were used to estimate the reservoir fluid volume. These parameters were imputed into the following formula.
\(V_{b}\) = Bulk reservoir volume (bbl) = 7758Ah.
7758 = bbl\acre-ft.
A = Reservoir cross-sectional area; acres (obtained from map data).
h = Reservoir thickness (pay zone; ft) (obtained from log data).
ɸ = Formation porosity (fraction) (obtained from log data).
NTG = Net-to-Gross ratio.
SW = Formation water saturation (fraction) (obtained from log data)
So = oil saturation.
Bo = Oil formation volume factor (1.2 bbls/stb for this work).
Results and discussion
Stratigraphic correlation and interpretation
Lithostratigraphic correlation was used across the four wells (Fig. 5). This was employed using the suite of wireline log signatures (i.e. gamma ray (GR), spontaneous potential (SP), bulk density (RHOB) and neutron-hydrogen porosity index (NPHI) logs). It provides general knowledge of the subsurface stratigraphic sequences in the Otigwe Field. The correlated top and base of the sandstone reservoirs (yellow colours in the well logs) for reservoir A and B show the lateral continuity of the stratigraphic sequences in time and space. It establishes both the stratigraphic principle of lateral continuity of strata and Walther’s law of facies succession. Reservoir A shows a slight uniform thickness across well 2, 7 and 11, except well 9. On the other hand, reservoir B is thinner in well 2, well 9 and well 11, except in well 7. Pinch-out is deciphered to exist toward well 11.
Well log analysis
The interpreted well logs for the four wells indicate that the reservoir rocks are generally unconsolidated sandstone with intercalation of interbedded shale sequences within each of the reservoir interval. According to (Etu-Efeotor 1997), well logs are basically used in the identification and characterisation of subsurface lithology and type of reservoir fluids (oil, gas and water). The lithologic sequences are delineated with the aid of the gamma ray (GR) and spontaneous potential (SP), whereas the unconsolidated nature of the reservoir rock was delineated with the aid of the calliper log, indicating the presence of caves. Also, the types of reservoir fluid were determined using resistivity (ILD), bulk density (RHOB) and neutron-porosity hydrogen index (NPHI) logs. Resistivity logs (ILD) can also be used to delineate lithology, such that lower resistivity depicts shale or clay and medium–high resistivity depicts sand or gravel containing fresh formation water (Wei et al. 2014). Although, Passey et al. (1990) stated that resistivity log signatures have less application in shale identification because the mineralogical content in shale is not fully understood. Hence, the log tools used for lithologic identification in this study were gamma ray and spontaneous potential log signature. Having provided a distinction between the reservoir and non-reservoir rock with the suite of well logs, the hydrocarbon water contacts across the four wells were delineated using resistivity and neutron-density log.
Gamma ray log reflects the amount of natural radioactive content (e.g. potassium, Uranium and Thorium) in rock (Etu-Efeotor 1997). Radiation emanates from these radioactive elements. All rock contains radioactive content, but shale has the highest radioactive content compare to sandstone and limestone (Etu-Efeotor 1997). The result of the four logs in Fig. 5 shows that a deviation of the gamma ray log to the right of the shale baseline indicates shale layers whereas a deviation to the left of the shale baseline indicates sandstone layers. This is because sandstones are free of shaly material and has low radioactive contents. As the radioactive material in the sandstone layer increases, the gamma ray signature increases to the right. Hence, the increase is proportional to the quantity of shale present. On the logs, some intervals are found to be shaly-sand and sandy-shale. These intervals generally have radioactive material that falls between clean sands and shales.
Spontaneous potential log records the potential difference between two electrodes and it is used to identify permeable and impermeable zones (Dewan 1983). It is measured in millivolt, negative at the left and positive at the right. When a permeable zone is encountered, the spontaneous potential log signature deflects to the negative with respect to the impermeable zone (e.g. shale) while for an impermeable zone, it deflects to the positive with respect to the permeable zone (e.g. sandstone). In this study, the permeable and impermeable zones in the suites of four available well logs (Fig. 5) represent unconsolidated sandstone and shale, respectively. This affirms the lithological sequence identified in the Niger Delta (Short and Stauble 1967).
The resistivity log was used in the identification of the hydrocarbon-bearing reservoirs (unconsolidated sandstone reservoir). The resistivity of a rock or formation is a measure of the ability to which it can resist or impede the flow of electric current. Formation water conducts electricity because it is a function of salinity (Archie 1942; Bridge and Demicco, 2008). On the other hand, hydrocarbon fluids which are non-conductive increases the resistivity values, as the void spaces within the rock become fully saturated with hydrocarbon (oil or gas). The resistivity log signatures were observed to be evidently higher within the hydrocarbon-bearing zones than in the formation water saturated zone (Fig. 5).
In general, sandstones basically have a relatively low density because of their relatively high porosity (Bridge and Demicco, 2008). The presence of gas within the pore spaces of the sandstone will lead to an extra density decrease; hence, there will be decrease in the neutron-porosity signature. This decrease will cause the neutron-porosity signature to cross over the bulk density signature (Bridge and Demicco, 2008). The decrease in both the neutron-porosity and bulk density signatures indicates the presence of gas in the reservoir, and this creates a large separation and forms a balloon shape (Etu-Efeotor 1997). The gas effect is formed because gas comprises a smaller amount of hydrogen atoms compare to oil and water (Etu-Efeotor 1997). Analysis of well logs indicates the presence of oil zones in both reservoirs and the absence of gas zones. Oil was found at a depth range of 3523 m to 3574 m in reservoir A and at a depth range of 2976 m to 2999 m in reservoir B across the four wells using the resistivity, neutron-porosity and bulk density logs. The presence of oil (green colour in the well logs) is indicated where there is separation between the neutron-porosity and bulk density logs, in addition to the high resistivity, whereas below this oil zone is the water zone having low resistivity (Fig. 7).
The oil–water contact is the surface in a subsurface reservoir separating the oil from the water. According to Okolie and Ujanbi (2007), evaluation of oil–water contact within the Niger Delta reservoir is difficult due to the presence of interbedded shale layers in the reservoir. In this study, the oil water contacts across the four wells in Fig. 5 were determined using the resistivity and combination of the neutron-porosity and bulk density logs. From the log analysis, the oil water contacts across well 2, well 7, well 9 and well 11 in reservoir A were found to be 3570 m (11713 ft), 3570 m (11713 ft), 3576 m (11732 ft) and 3580 m (11745 ft), respectively, whereas for reservoir B, the oil water contacts were found to be 3008 m (9869ft), 3002 m (9849 ft), 2985 m (9793 ft) and 3001 m (9846 ft), respectively. Estimation of these oil water contacts is very important for reservoir characterization and evaluation of original oil in place, since it aids in the determination of the oil section (Archer 1986; Adams 1993). This height/thickness of the oil section (from top of reservoir to the oil–water contact) was used in the estimation of the stock tank oil in place in this study.
Structural interpretation on seismic sections
Network of several normal faults was seen across the entire seismic sections (Figs. 8 and 9). Fourteen (14) of these normal faults were mapped and were found to trend northwest-southeast and dip southwest-southeast. It was observed that the down thrown blocks are slightly thicker than the correlative counterpart of the upthrown blocks. This is attributed to successive stages of growth (Childs et al. 2003). This implies that the rock volume or strata in the Niger Delta were formed contemporaneously and continuously as deposition progresses. According to Lin et al. (2004), such faults are called syn-depositional extensional faulting, also called growth faults. It was also observed that the faulting is associated with anticlinal traps (rollover anticline) across some parts of the seismic sections. The growth fault-rollover anticline structural systems result from finite amplitude gravitational instability having three different stages of formation, which include; birth, growth and decay (Mauduit and Brun 1998). The fault-supported anticlinal structural features in the field were probably responsible for the dispersion and distribution pattern of sediment and succession of depositional sequences in the basin.
Interpretation of petrophysical properties
Simulation results of petrophysical properties
Reservoir simulation and modelling software was also used to estimate the petrophysical properties (Tables 2 and 3). The averages of these modelling results are shown (Table 4).
Analytical computation of petrophysical properties from well log
The formulas presented in data set and methods (Eq. 1 to Eq. 11) were applied for the determination of the various petrophysical properties (Tables 5 and 6, see computation in Appendix A). The prolific well for commercial purpose was identified to be well 7 from reservoir A, using the factor hɸeffSo (Table 5). Oil well placement within a grid block of a reservoir model can be determined by the hɸeffSo factor. The average calculated petrophysical properties are shown below (Table 7).
The shale volume determination in the preceding section account for the effect of shale contents within the unconsolidated sandstone reservoir and to ascertain the quality of the reservoir within the Otigwe field, coastal swamp depositional belt of the Niger Delta. The essentiality of determining the shale volume is critical, because it helps in the computation of net-to-gross ratio, porosity and water saturation (Adeoti et al. 2009). The result of the shale volume was used to reduce the volume of the unconsolidated sandstone reservoir in the Otigwe field by correcting for the present of shale using net-to-gross ratio, since there is a direct relationship between shale volume and net-to-gross. This net-to-gross ratio, porosity and water saturation were then used for the volumetric estimation of the reservoir fluids for proper estimation of hydrocarbon.
The total and effective average porosity determined indicate that the reservoir in the Otigwe Field ranges from good to very good. The net-to-gross ratio is an engineering correction factor or term use to reduce the volume of the unconsolidated sandstone reservoir in the location of study by correcting the volume of shale.
Time and depth structural maps
The subsurface time and depth structural maps of the horizons of interest (top of reservoir A and B) were constructed by posting the time, depth and fault values on the seismic base map of the Otigwe Field (Figs. 10, 11, 12, and 13). From the depth structural maps, it was observed that the contour values where the reservoirs are situated have an anticlinal structural trap with network of faults.
Determination of volumetric estimation
The computation of the volumetric estimation in this study was done in both reservoir and surface conditions. Hydrocarbon reserves or volume of hydrocarbon can be estimated using deterministic and stochastic methods. Based on limited number of available data and geological complexities of the subsurface reservoir, there is always uncertainty in the use of these methods of estimation. These uncertainties also reflect on the volumetric estimation of resource or reserve. Therefore, resources are expected to be estimated by the application of both deterministic and stochastic methods. However, in this study, in addition to the approximation made (earlier discussed), deterministic method was used for the analytical method, to determine the volume of hydrocarbon in place, since it is by far the most common. The procedure involves the selection of a single value for each reservoir parameter and input the values into one or more than one simple and appropriate equations, thereby obtaining a single answer. Simple and appropriate equations were used to obtain petrophysical parameters, such as porosity, permeability, water saturation, net-to-gross ratio, volume of shale, and gross rock volume. These estimated reservoir parameters and results from seismic interpretation were integrated to obtain a single value for the hydrocarbon pore volume (HCPV) at reservoir condition in both reservoirs A and B. This gives a description of the volume of hydrocarbon that filled the pore spaces inside the reservoir and the change in volume that will take place. This was then converted to volume of hydrocarbon at surface condition (OOIP or STOIIP) using the appropriate oil formation volume factor of 1.2 bbl/stb. The estimated volume of hydrocarbon was calculated directly using average values of the petrophysical parameters, which include; average effective porosity, average oil saturation, average net-to-gross ratio, average of the reservoir thickness in the pay zone and the reservoir cross-sectional area occupied by oil. The average values from these parameters were then substituted into Eq. (10) to obtain the original oil in place (OOIP) or stock tank oil initially in place (STOIIP) at surface condition for both reservoir A and B.
On the other hand, for the simulation model results, geostatistical method was used to populate or distribute the reservoir properties, based on Sequential Gaussian Simulation, which considered variogram analysis. The procedure or methods was done in such a way that the properties at well points where upscaled into the 3D grid and the reason for the upscale is to average the properties to feel up the grid cells. After then, the data or variogram analysis was done to see the variation of the data from one point to another (that is, how far the data could remain from point of stationarity or well point to a distance, before it changes to something different). Having understood the data differences, it was now geostatistically distributed based on neighbour to neighbour cell changes across the grids (that means that, the cells that are closed to the well point or point of reference or point of stationarity, actually have small features or data similarity and the distribution varies based on the variogram distribution or spread). The properties that were distributed include; the porosity, water saturation, net-to-gross ratio, permeability, etc. This process is called a stochastic method, because at each point, there is a variation of data across the grids and not a single property. This was done for each of the reservoir properties.
Thereafter, model-based calculation was done for each of the grid cells to calculate the volume per cell using the models which comprise each variation of data per cell across the grids. The basic equation of calculating STOIIP was still used but the basic difference between the stochastic and the deterministic method is that the deterministic method used only a single value (no variation of data—which may really not be realistic due to reservoir heterogeneity resulting from facies change) whereas the stochastic method considered the established variations of STOIIP for each cells across the grids, taking into consideration, the cumulative STOIIP.
Simulated result of volumetric estimation of reservoir Fluids
The simulated result of the stock tank oil initially in place (STOIIP) (Table 8) indicates that reservoir A is more prolific compared to reservoir B.
Analytical result of volumetric estimation of reservoir fluids
Computation of the area covered with hydrocarbon
To compute the volume analytically, firstly, the areas of reservoir A and B were calculated from the depth structural map (Figs. 10 and 11). The depth structural maps were divided into squared grids and the area per grid was computed to be 200 m by 200 m (Area = 40,000 m3) using the survey lines instead of the scale 1:78,125, to avoid printing error. The survey lines were traced from the reservoir simulation and modelling software and seem accurate. The area in metre was then converted to acre (40,000m3 = 9.88 acres). The grids in the maps were counted within the oil region, taking into consideration the average of the oil water contacts and the average of the reservoir tops across the four wells. The total oil area for each reservoir was then obtained by multiplying the total number of squared box containing oil to the area of a single squared box. Hence, the prospect area for each reservoir is as follows:
-
Area of oil region in reservoir A = 9.88 acres × 40 squared grids = 395.20 acres
-
Area of oil region in reservoir B = 9.88 acres × 31 squared grids = 306.28 acres
Volumetric estimation of hydrocarbon in reservoir A and B using analytical method
The volumetric determination approach observes the geological information to estimate the hydrocarbon pore volume and original oil in place. The hydrocarbon pore volume estimation in this study acknowledged the static method by deriving its source of data from wireline logs and geological base map of the Otigwe field where the four available logs were located. Thereafter, the formation volume factor was used to convert the hydrocarbon pore volume at reservoir condition to original oil in place at surface condition (STOIIP). Using the average petrophysical properties (Table 7), the computations and results presentation for reservoir A and B are illustrated below using Eqs. 9 and 10:
Volumetric estimation at reservoir condition
Volumetric estimation at surface condition
Reservoir A
Reservoir B
Comparing the simulated and analytical STOIIP results
The simulated result of the stock tank oil initially in place (STOIIP) indicates that reservoir A is more prolific compared to reservoir B. Secondly, comparing the simulated STOIIP result with that of the STOIIP obtained analytically, it was observed that the results for both methods were closely related (Table 9).
Conclusion
Integrated suites of well logs and 3D seismic data were used to characterise two hydrocarbon-bearing reservoir sand bodies across four wells in the Otigwe Field, coastal swamp depobelt, Niger Delta. The reservoir characterisation and volumetric estimation of the hydrocarbon within the reservoir sand bodies were made possible through the creation of time and depth subsurface structural maps of two horizons of interest using the reservoir simulation and modelling software. The time and depth subsurface structural maps provide more detailed structural architecture and regions of possible hydrocarbon accumulation within the fault-supported anticlinal trap. This means, faulting and folding were the main trapping mechanism in the study area and the four available wells were drilled through these traps where most of the entrapped hydrocarbons exist.
The reservoir properties of reservoir A and B in the Otigwe field indicates that the formation has the potential to accumulate reasonable quantity of hydrocarbon, since the porosity, permeability, high oil saturation and low water saturation values are exceptional, coupled with the right entrapment conditions. From the analytical method, the identified hydrocarbon-bearing reservoir zones have porosity, permeability and hydrocarbon (oil) saturation ranging from 15 to 26%, 893.23 mD to 2323.82 mD and 75% to 92% for reservoir A and 18% to 26%, 920.20 mD to 1675.79 mD and 43% to 92% for reservoir B, respectively. Furthermore, using the analytical method, the estimated reservoir fluid volume (STOIIP) at surface condition for reservoir A is 52.58 MMstb and for reservoir B is 18.85 MMstb, while the average net-to-gross ratio and shale volume for reservoir A and B are 0.78 and 0.22, respectively. On the other hand, from the static model, the identified hydrocarbon-bearing reservoir zones have porosity, permeability and hydrocarbon (oil) saturation ranging from 17 to 24%, 103.10 mD to 1783.28 mD and 68% to 79% for reservoir A and 15% to 24%, 138.14 mD to 1841.58 mD and 45% to 79% for reservoir B, respectively. Also, the simulation results from reservoir simulation and modelling software tool show that the estimated reservoir fluid volume (STOIIP) at surface condition for reservoir A is 59MMstb and for reservoir B is 25.70MMstb. The average net-to-gross ratio and shale volume for reservoir A ranges from 0.86 to 0.89 and 0.11 to 0.14, respectively, while for reservoir B the range is between 0.69 to 0.82 and 0.18 to 0.31, respectively. The estimated reservoir fluid volume using both methods showed similar results. The study shows that reservoir A is more prolific compare to reservoir B.
From the petrophysical parameters, it can be observed that the two reservoirs A and B are not uniform due to subsurface reservoir heterogeneity, in addition to the compartmentalization with faults and probably fractures which can complicate fluid flow. Hence, to reduce uncertainty and improve or optimize STOIIP for further studies, it will be ideal to integrate biostratigraphic data and core samples, analyse these data and drill more wells around the anticlinal structure. According to Fadiya et al. (2014), biostratirgaphic data play a core role in the integrated characterization and modelling of lateral continuity of reservoir lithofacies by providing accurate interpretation of the subsurface reservoir framework, which aid in decision-making during drilling operation. Hence, with the addition of the biostratigraphic data and core samples in Otigwe Field, a precise and more detailed reservoir characterization and volumetric estimation will be established.
Implication of the study
From the study, it was discovered that reservoir A and B are not homogenous, as can be seen from their variable petrophysical parameters (porosity, permeability, etc.), coupled with the presence of network of faults around the anticlinal structural trap which although indicate that the geometry or architecture of the reservoir is good for hydrocarbon accumulation but these network of faults and probably the presence of fractures can cause compartmentalization, which can lead to complication in fluid flow. Therefore, it will be ideal for more wells to be drilled around the fault-supported anticlinal structural trap, in addition to collecting and analysing core samples and integrate these core samples with biostratigraphic data to enhance or optimize the STOIIP in the Otigwe field.
Availability of data
This manuscript is an original work conducted by the authors under close supervision, which restrict data transferability by Moni Pulo (Petroleum Development Limited).
References
Abbaszadeh M, Takano O, Yamamto H, Shimamoto T, Yazawa N, Sandria FM, Zamora Guerrero DH, de la Garza, Fernando R (2003) SPE annual technical conference and exhibition, Integrated geostatistical reservoir characterization of turbidite sandstone deposits in Chicontepec Basin, Gulf of Mexico. Soc Pet Eng. https://doi.org/10.2118/84052-MS
Adams SJ, Van den Oord RJ (1993) Capillary pressure and saturation height functions. Report EP 93–0001, SIPM BV
Adejobi AR, Olayinka AI (1997) Stratigraphy and hydrocarbon potential of the Opuama channel complex Area, Western Niger Delta. Niger Assoc Pet Explor (NAPE) Bull 12:1–10
Adeoti L, Ayolabi E, James P (2009) An Integrated approach to volume of shale analysis: Niger Delta example, offrire field. World Appl Sci J 7:448–452
Aizebeokhai A, Olayinka I (2011) Structural and stratigraphic mapping of EMI field, offshore Niger Delta. J Geol Mining Res 3:5–38
Ajisafe YC, Ako BD (2013) 3D Seismic attributes for Reservoir Characterization of “Y” field Niger Delta Nigeria. J Appl Sci 18:86–102
AL-Awad M, (2001) Evaluating uncertainty in Archie’s water saturation equation parameters determination methods. Soc Pet Eng. https://doi.org/10.2118/68083-MS
Al-Ruwaili (2007) Accuracy of shaly sand formation evaluation. United States Patent, Patent no. US 7,168,310 B2
Archer JS, Wall CG (1986) Petroleum engineering principles and practice. Grayer and Trotman, London
Archie GE (1942) The electrical resistivity log as an aid in determining some reservoir characteristics. Trans AIME Soc Pet Eng 146:1–9. https://doi.org/10.2118/942054-G
Barde JP, Gralla P, Harwijanto J, Marsky J (2002) Exploration at the eastern edge of the prescapian basin impact of data integration on Upper Permian and Triassic prospectivity. Am Assoc Petrol Geol Bull 86:399–415. https://doi.org/10.1306/61EEDAEE-173E-11D7-8645000102C1865D
Bridge J, Demicco R (2008) Earth surface processes. Cambridge University Press, Landforms and Sediment Deposits
Childs C, Nicol A, Walsh JJ, Watterson J (2003) The Growth and Propagation of Synsedimentary Faults. J Struct Geol 25:633–648
Dewan JT (1983) Essentials of Modern Open-Hole Log Interpretation. Pennwell Publishing Company, Tulsa, Oklahoma
Doust H (1989) The Niger Delta hydrocarbon potential, a major Tertiary Niger Province. In: Proceedings of KNGMG symposium, coastal lowstands, Geology and Geotechnology, The Hague. Kluiver Academic Publishers, Dordrecht, pp 22–25
Doust H and Omatsola E (1990). Niger Delta. In: Edwards JD, Santogrossi PA, (eds) Divergent/passive margin Basins. American Association of Petroleum Geology Memoir 48: Tulsa, American Association of Petroleum Geologists, pp 239–248
Etu-Efeotor JO (1997) Summarised geology of the Niger Delta. Fundamental of Petroleum Geology, Jeson Services, Port Harcourt
Evamy BD, Haremboure J, Kamerling P, Knaap WA, Molloy FA, Rowlands PH (1978) Hydrocarbon habitat of Tertiary Niger Delta. Am Asso Petrol Geol Bull 62:277–298
Fadiya SL, Jaiyeola-Ganiyu FA, Fajemila OT (2014) Foraminifera Biostratigraphy and Paleoenvironment of Sediments from Well AM-2, Niger Delta. Ife J Sci 16(1):61–72
Ijasan O, Torres-Verdín C, Preeg WE (2013) Interpretation of porosity and fluid constituents from well logs using an interactive neutron-density matrix scale. Interpretation. https://doi.org/10.1190/INT-2013-0072.1
Kulke H (1995) Regional petroleum geology of the world. Part II: Africa, Australia and Antarctica. Berlin, Gebruder Bogrntraeger, pp 143–172
Lin C, Zheng H, Ren J, Liu J, Qiu Y (2004) The Control of Syndepositional Faulting on the Eogene Sedimentary Basin Fills of the Dongying and Zhanhua Sags, Bohai Bay Basin. Sci China Ser d Earth Sci-Eng Ed 47:769–782
Mauduit T, Brun JP (1998) Growth fault/rollover systems: birth, growth, and decay. J Geophys Res Solid Earth 103:8B
Moradi S, Moeini M, Al-Askari MK, Mahvelati EH (2016) Determination of shale volume and distribution patterns and effective porosity from well log data based on cross-plot approach for a shaly carbonate gas reservoir. IOP Conf Ser Earth and Environ sci 44:042002. https://doi.org/10.1088/1755-1315/44/4/042002
Okolie E, Ujanbi O (2007) Estimation of height of oil-water contact above free water level using capillary pressure method for effective classification of reservoirs in the Niger Delta. Nigerian J Phys 9:303–311
Oluwajana OA, Ehinola OA, Okeugo CG, Adegoke O (2017) Modeling hydrocarbon generation potentials of eocene source rocks in the agbada formation, Northern Delta Depobelt, Niger Delta Basin, Nigeria. J Pet Exp Product Technol 7:379–388
Owolabi O, LongJohn T, Ajienka J (1994) An empirical expression for permeability in unconsolidated sands of the eastern Niger Delta. J Pet Geol. https://doi.org/10.1111/j.1747-5457.1994.tb00117.x
Passey Q, Creaney S, Kulla J, Moretti F, Stroud J (1990) A practical model for organic richness from porosity and resistivity logs. AAPG Bull 74:1777–1794. https://doi.org/10.1306/0C9B25C9-1710-11D7-8645000102C1865D
Short K, Stauble A (1967) Outline of geology of Niger Delta. AAPG Bull 51:761–779
Stacher P (1995) Present understanding of the Niger Delta hydrocarbon habitat. In: Oti MN, Postma G (eds) Geology of Deltas. Rotterdam, AA Balkema
Szabo N (2011) Shale volume estimation based on the factor analysis of well-logging data. Acta Geophys. https://doi.org/10.2478/s11600-011-0034-0
Tuttle ML, Charpentier RR, Brownfield ME (1999) The Niger Delta petroleum system. Niger Delta province, Nigeria, Cameroon, and Equatorial Guinea, Africa, US Department of the Interior, US Geological Survey
Weber MR (2012) A detailed well log and 3D seismic interpretation of the fruitland formation: Southwest regional partnership carbon sequestration site, San Juan basin, New Mexico. Master thesis. West Virginia University
Wei Y, Jianbo W, Shuai L, Kun W, Yinan Z (2014) Logging Identification of the Longmaxi Mud Shale Reservoir in the Jiaoshiba Area. Sichuan Basin Nat Gas Ind B 1(1):230–236. https://doi.org/10.1016/j.ngib.2014.11.016
Funding
The author (s) received no funding for this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Ethics approval
Ethics approval has been followed accordingly.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Analytical computation of shale volume
Applying Eq. (1) and Eq. (2) for tertiary or younger rock, the computation is shown as follows:
Reservoir A | Reservoir B |
|---|---|
Well 2 | |
\({\text{I}}_{{{\text{GR}}}} = \frac{{52.5 - 20}}{{85 - 20}} = 0.5{\text{~}}\) | \({\text{~I}}_{{{\text{GR}}}} = \frac{{53 - 31}}{{75 - 31}}{\text{~}} = 0.5\) |
\({\text{V}}_{{{\text{sh}}}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) | \(~V_{{sh}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) |
Well 7 | |
\({\text{I}}_{{{\text{GR}}}} = \frac{{60 - 20}}{{100 - 20}} = 0.5{\text{~}}\) | \({\text{I}}_{{{\text{GR}}}} = \frac{{55 - 20}}{{90 - 20}}{\text{~}} = 0.5\) |
\({\text{V}}_{{{\text{sh}}}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) | \(V_{{sh}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) |
Well 9 | |
\({\text{I}}_{{{\text{GR}}}} = \frac{{60 - 22.5}}{{97.5 - 22.5}} = 0.5\) | \({\text{~I}}_{{{\text{GR}}}} {\text{~}} = \frac{{60.5 - 31}}{{90 - 31}} = 0.5\) |
\({\text{V}}_{{{\text{sh}}}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22~~\) | \(~V_{{sh}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) |
Well 11 | |
\({\text{I}}_{{{\text{GR}}}} = \frac{{62.5 - 20}}{{105 - 20}} = 0.5{\text{~}}\) | \({\text{I}}_{{{\text{GR}}}} = \frac{{81.25 - 65}}{{97.5 - 65}} = 0.5{\text{~}}\) |
\({\text{V}}_{{{\text{sh}}}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) | \(~V_{{sh}} = 0.083\left( {2^{{3.7 \times 0.5}} - 1} \right) = 0.22\) |
Analytical computation of total and effective porosity
Applying Eqs. (3) and (4) for total and effective porosities, respectively, the computation is shown as follows:
Reservoir A | Reservoir B |
|---|---|
Well 2 | |
\(\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.16}}{{2.65 - 0.8}} = 0.26\) | \(\phi _{{{\text{Total}}}} ~ = \frac{{2.65 - 2.12}}{{2.65 - 0.8}} = 0.29\) |
\(\phi _{{{\text{effective}}}} = 0.26\left( {1 - 0.22} \right) = 0.22\) | \(\phi _{{{\text{effective}}}} = 0.29\left( {1 - 0.22} \right) = 0.23\) |
Well 7 | |
\(\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.16}}{{2.65 - 0.8}} = 0.26\) | \(~\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.1}}{{2.65 - 0.8}} = 0.30\) |
\(\phi _{{{\text{effective}}}} = 0.26\left( {1 - 0.22} \right) = 0.20\) | \(\phi _{{{\text{effective}}}} = 0.30\left( {1 - 0.22} \right) = 0.23\) |
Well 9 | |
\(\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.3}}{{2.65 - 0.8}} = 0.19\) | \(~\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.1}}{{2.65 - 0.8}} = 0.23\) |
\(\phi _{{{\text{effective}}}} = 0.19\left( {1 - 0.22} \right) = 0.15~\) | \(\phi _{{{\text{effective}}}} = 0.23\left( {1 - 0.22} \right) = 0.18\) |
Well 11 | |
\(\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.2}}{{2.65 - 0.8}} = 0.24\) | \(\phi _{{{\text{Total}}}} = \frac{{2.65 - 2.16}}{{2.65 - 0.8}} = 0.26\) |
\(\phi _{{{\text{effective}}}} = 0.24\left( {1 - 0.22} \right) = 0.19~\) | \(\phi _{{{\text{effective}}}} = 0.26\left( {1 - 0.22} \right) = 0.20\) |
Saturation determination
Applying Eq. (5) and Eq. (6) for water and oil saturation, respectively, the computation is shown below with the following assumptions:
-
The reservoir is water wet
-
Water salinity is constant
-
Mud filtrate salinity is constant over the processed interval
Based on these assumptions, the resistivity of water for each of the oil well, cutting across reservoir A and B, is constant.
Reservoir A | Reservoir B | |
|---|---|---|
Well 2 | ||
In the water zone Sw = 1.0 | \(R_{w} = \frac{{1.0^{2} \times 0.20^{2} \times 4}}{{0.81}} = 0.20\;\Omega {\text{m}}\) | |
In the oil zone: | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.20}}{{0.20^{2} \times 100}}}} = 0.20 = 20\%\) | \(~{\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.20}}{{0.23^{2} \times 150}}}} = 0.14 = 14\%\) |
\({\text{S}}_{{\text{o}}} = 1 - 0.20 = 0.80 = 80\% ~\) | \({\text{S}}_{{\text{o}}} = 1 - 0.14 = 0.86 = 86\%\) | |
Well 7 | ||
In the water zone Sw = 1.0 | \(R_{w} = \frac{{1.0^{2} \times 0.20^{2} \times 3}}{{0.81}} = 0.15\Omega m\) | |
In the oil zone: | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.15}}{{0.20^{2} \times 50}}}} = 0.25 = 25\%\) | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.15}}{{0.23^{2} \times 150}}}} = 0.12 = 12\%\) |
\({\text{S}}_{{\text{o}}} = 1 - 0.25 = 0.75 = 75{\text{\% }}\) | \({\text{S}}_{{\text{o}}} = 1 - 0.12 = 0.88 = 88\%\) | |
Well 9 | ||
In the water zone Sw = 1.0 | \(R_{w} = \frac{{1.0^{2} \times 0.15^{2} \times 3}}{{0.81}} = 0.08\Omega m\) | |
In the oil zone: | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.08}}{{0.15^{2} \times 200}}}} = 0.12 = 12\%\) | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.08}}{{0.18^{2} \times 300}}}} = 0.08 = 8\%\) |
\({\text{S}}_{{\text{o}}} = 1 - 0.12 = 0.88 = 88\%\) | \({\text{S}}_{{\text{o}}} = 1 - 0.08 = 0.92 = 92\%\) | |
Well 11 | ||
In the water zone Sw = 1.0 | \(R_{w} = \frac{{1.0^{2} \times 0.19^{2} \times 3.5}}{{0.81}} = 0.16\Omega m\) | |
In the oil zone: | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.16}}{{0.19^{2} \times 300}}}} = 0.11 = 11\% ~\) | \({\text{S}}_{{\text{w}}} = \sqrt[2]{{\frac{{0.81 \times 0.16}}{{0.20^{2} \times 10}}}} = 0.57 = 57\%\) |
\({\text{S}}_{{\text{o}}} = 1 - 0.11 = 89\% {\text{~}}\) | \({\text{S}}_{{\text{o}}} = 1 - 0.57 = 0.47 = 47\%\) | |
Analytical computation of net-to-gross ratio
Applying Eq. (7), the computation is shown as follows:
Reservoir A | Reservoir B |
|---|---|
Well 2 | |
\({\text{NTG}} = 1 - 0.22 = 0.78\) | \(NTG = 1 - 0.22 = 0.78\) |
Well 7 | |
\({\text{NTG}} = 1 - 0.22 = 0.78~\) | \(NTG = 1 - 0.22 = 0.78\) |
Well 9 | |
\({\text{NTG}} = 1 - 0.22 = 0.78\) | \(NTG = 1 - 0.22 = 0.78\) |
Well 11 | |
\({\text{NTG}} = 1 - 0.22 = 0.78\) | \(NTG = 1 - 0.22 = 0.78\) |
Analytical computation of permeability
Applying Eq. (8), the computation is shown as follows:
Reservoir A: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.20} \right)^{2} - 34540\left( {0.20} \right)^{2} \left( {0.20} \right)^{2} + 307 = 1313.82\;{\text{mD}}\).
Reservoir B: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.23} \right)^{2} - 34540\left( {0.23} \right)^{2} \left( {0.14} \right)^{2} + 307 = 1675.79\;{\text{mD}}\).
Well 2
Reservoir A: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.20} \right)^{2} - 34540\left( {0.20} \right)^{2} \left( {0.20} \right)^{2} + 307 = 1313.82\;{\text{mD}}\).
Reservoir B: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.23} \right)^{2} - 34540\left( {0.23} \right)^{2} \left( {0.14} \right)^{2} + 307 = 1675.79\;{\text{mD}}\).
Well 7
Reservoir A: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.20} \right)^{2} - 34540\left( {0.20} \right)^{2} \left( {0.25} \right)^{2} + 307 = 1282.73\;{\text{mD}}\).
Reservoir B: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.23} \right)^{2} - 34540\left( {0.23} \right)^{2} \left( {0.12} \right)^{2} + 307 = 1685.29\;{\text{mD}}\).
Well 9
Reservoir A: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.15} \right)^{2} - 34540\left( {0.15} \right)^{2} \left( {0.12} \right)^{2} + 307 = 893.23\;{\text{mD}}\).
Reservoir B: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.18} \right)^{2} - 34540\left( {0.18} \right)^{2} \left( {0.08} \right)^{2} + 307 = 1160.12\;{\text{mD}}\).
Well 11
Reservoir A: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.19} \right)^{2} - 34540\left( {0.19} \right)^{2} \left( {0.11} \right)^{2} + 307 = 1250.44\;{\text{mD}}\).
Reservoir B: \(K\left( {{\text{mD}}} \right) = 26552\left( {0.20} \right)^{2} - 34540\left( {0.20} \right)^{2} \left( {0.57} \right)^{2} + 307 = 920.20\;{\text{mD}}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kurah, B.K., Shariatipour, M.S. & Itiowe, K. Reservoir characterization and volumetric estimation of reservoir fluids using simulation and analytical methods: a case study of the coastal swamp depobelt, Niger Delta Basin, Nigeria. J Petrol Explor Prod Technol 11, 2347–2365 (2021). https://doi.org/10.1007/s13202-021-01206-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-021-01206-1