Introduction

With the growing economic, logistical and environmental challenges for the development and maintenance of hydrocarbon resources, the need for good drilling, recovery, and stimulation strategies has been increasing. The events of induced seismicity and soil deformation recorded around oil fields have led to increasing awareness of the sensitivity of reservoirs to the state of stresses. It has become increasingly clear that an understanding of the evolution of these stresses is essential to maximize production from existing fields and to develop future fields (Bubshait et al. 2018).

For a long time, the deformation of petroleum reservoirs was only assessed when the subsidence of the surface generated operational problems or became a threat to the integrity of the field. Some well-known cases include Willmington Field in California and Ekofisk Field in the North Sea (Settari 2002).

In the last few decades, the development of stress-sensitive formations is raising awareness that reservoir geomechanics is an essential aspect for managing petroleum reservoirs. A reservoir sensitive to the state of stress presents significant changes in its structure and properties, such as porosity and permeability, due to the change in effective stress or pressure. These changes are large enough to affect the production or impose risks of damaging the wells (Pan 2009).

The understanding of reservoir geomechanical behavior is becoming increasingly important for the petroleum industry. It has been reported that significant changes in pore pressure due to depletion or injection in weak formations lead to a great change in effective stress. For poorly compacted reservoirs, the stress changes have beneficial effects on fluid recovery due to the reservoir compaction. However, the reservoir compaction can also reduce reservoir permeability, cause surface subsidence and create damage to well equipment. Stress changes particularly affect fractured and faulted reservoirs and may enhance/reduce fracture conductivity or create preferred flooding directions, close and open of preexisting fractures, fault reactivation (Hamid et al. 2017; Mainguy and Longuemare 2002).

Besides, recent exploratory activities tend to discover weak reservoirs in increasingly deep water with high pressure and temperature, where compaction is an important issue. As deeper reservoirs are developed in deeper water, with expensive wells and equipment, there is an increasing need to improve engineering and modeling technologies to address possible geomechanical problems at the planning stage of these fields (Settari 2002).

Coupled geomechanical modeling techniques have advanced from research code to commercial software. Coupled analyses can predict, for example, reservoir volume deformation and its impact on porosity and permeability, the potential for fault reactivation, and other effects that cannot be accounted for by conventional reservoir simulation. Therefore, coupled geomechanical analyses are useful to determine under which conditions geomechanical effects should be considered in the reservoir simulation to improve production forecasts. It is also possible to predict compaction and subsidence, ensure well integrity, reduce risks of fault reactivation and out-of-zone hydraulic fracture propagation during fluid injection processes (Serra De Souza and Lima Falcão 2015).

The main challenge in the evaluation of the variation of reservoir volume is how to quantify its impact on oil production. How to decide whether a coupled analysis is important or not? Many reservoirs have compaction as an oil recovery mechanism, and since compaction is normally not taken into account in conventional reservoir simulation, its impact on history match and prediction of oil production can be huge for those reservoirs (Serra De Souza and Lima Falcão 2015).

However, the coupled modeling of large-scale multiphase problems could be computationally expensive. For a long time, the petroleum industry has considered these analyses not feasible to apply in problems of practical interest. To minimize this drawback, various coupled modeling approaches have been developed to consistently consider the geomechanical effects in reservoir simulation in affordable computational times (Chen et al. 1995; Inoue and Fontoura 2009b; Longuemare et al. 2002; Samier et al. 2007; Settari et al. 2001; Stone et al. 2003; Thomas et al. 2003; Tran et al. 2002).

The hydromechanical coupling can be achieved either by a fully or partially coupled numerical scheme. The fully coupled approach performs the flow and displacement calculations simultaneously. The software solves both the flow and geomechanical variables in the same system of equations. These normally results in high computational cost and code development (Giani et al. 2018; Kim 2010).

Alternatively, the partially coupled approach consists of the external coupling between different numerical simulators. A conventional reservoir simulator based on the finite difference method solves the flow problem, and a finite element model runs the stress equilibrium equations, respectively. This numerical scheme solves the stress and flow equations separately for each time step of the analysis and passes information between the two simulators through an interface code. Thereby, flow parameters that depend on the stress state, such as porosity and permeability, can be updated in the reservoir simulation (Amirlatifi 2013; Giani et al. 2018; Kim 2010).

The partially coupled approach looks more flexible than the fully coupled approach and can significantly reduce the computation cost of the coupled analysis. The number of stress-displacement simulation runs can be reduced depending on the frequency in which the two simulators are coupled (Amirlatifi 2013; Dean et al. 2006). Besides, this technique benefits from high developments in physics and numerical techniques of both flow and mechanical simulators (Kim, 2010).

Therefore, the current study applies a two-way explicit partial coupling methodology between flow and mechanical simulators to quantify the impact of the rock deformation on fluid recovery. A Brazilian sandstone reservoir (Namorado Field -Campos Basin) was chosen to run the coupled analyses under different injection/depletion scenarios and under different reservoir stiffness to assess the conditions in which geomechanical effects are important for the production of this reservoir.

The main highlight of this paper is to evaluate the geomechanical effects under real production conditions, in a heterogeneous reservoir and under a multiphase flow regime. Most of the published results are for small-scale problems and relatively simple multi-physics interactions. Besides, the use of the explicit coupling scheme allows improving the computational time of coupled analyses.

Theoretical background

Reservoir multiphase flow model

The governing equations for the fluid flow model are expressed along the standard lines of petroleum reservoir simulation, known as black oil simulation. The overall composition of the three possible fluid phases (water, oil, and gas) stays the same throughout the simulation (Peaceman 1977).

Based on the conservation of mass for each phase and Darcy’s law, the multiphase flow equations are described from Eqs. (1) to (3), where w, o, and g refer to the water, oil, and gas phases, respectively.

$$\nabla \cdot [\lambda_{{\text{w}}} (\nabla p_{{\text{w}}} - \gamma_{{\text{w}}} \nabla z)] = \frac{\partial }{\partial t}\left( {\frac{{\phi S_{{\text{w}}} }}{{B_{{\text{w}}} }}} \right) + q_{{\text{w}}}$$
(1)
$$\nabla \cdot [\lambda_{{\text{o}}} (\nabla p_{{\text{o}}} - \gamma_{{\text{o}}} \nabla z)] = \frac{\partial }{\partial t}\left( {\frac{{\phi S_{{\text{o}}} }}{{B_{{\text{o}}} }}} \right) + q_{{\text{o}}}$$
(2)
$$\nabla \cdot [R_{{{\text{so}}}} \lambda_{{\text{o}}} (\nabla p_{{\text{o}}} - \gamma_{{\text{o}}} \nabla z) + \lambda_{{\text{g}}} (\nabla p_{{\text{g}}} - \gamma_{g} \nabla z)] = \frac{\partial }{\partial t}\left[ {\phi \left( {\frac{{R_{{{\text{so}}}} S_{{\text{o}}} }}{{B_{{\text{o}}} }} + \frac{{S_{{\text{g}}} }}{{B_{{\text{g}}} }}} \right)} \right] + R_{{{\text{so}}}} q_{{\text{o}}} + q_{{\text{g}}}$$
(3)
$$\lambda_{{\text{p}}} = \frac{{k_{{{\text{rp}}}} }}{{\mu_{{\text{p}}} B_{{\text{p}}} }}K\quad p = w,o,g$$
(4)
$$S_{{\text{o}}} + S_{{\text{g}}} + S_{{\text{w}}} = 1$$
(5)

where \(\gamma_{{\text{p}}} = \rho_{{\text{p}}} {\mathbf{g}}\); \(\rho_{{\text{p}}}\) = phase density; \({\mathbf{g}}\) = acceleration due to gravity; \(k_{{{\text{rp}}}}\) = relative permeability; \(K\) = absolute permeability; \(\mu_{{\text{p}}}\) = viscosity; \(B_{{\text{p}}}\) = formation volume factor; \(p_{{\text{p}}}\) = phase pressure; \(z\) = depth; \(\phi\) = porosity; \(S_{{\text{p}}}\) = phase saturation; \(q_{{\text{p}}}\) = mass rate of injection or production; \(R_{{{\text{so}}}}\) = solubility of gas in oil.

The fluid pressure computed by Eqs. (1–3) is directly related to porosity, while the permeability has a strong influence on flow velocity and saturation. Once the porosity is a function of pressure and time, the porosity variation can be rewritten in terms of the pore compressibility (\(c_{{\text{p}}}\)), as expressed in Eqs. (6–7).

$$c_{{\text{p}}} \equiv \frac{1}{\phi }\left( {\frac{\partial \phi }{{\partial p}}} \right)$$
(6)
$$\frac{\partial \phi }{{\partial t}} = \frac{\partial \phi }{{\partial p}}\frac{\partial p}{{\partial t}} = \phi c_{{\text{p}}} \frac{\partial p}{{\partial t}}$$
(7)

Then, the correlation in Eq. (8) is used to account for porosity variation as a function of the pressure and pore compressibility.

$$\phi = \phi_{0} [1 + c_{{\text{p}}} (p - p_{0} )]$$
(8)

where \(\phi_{0}\) = initial porosity; \(p_{0}\) = reference pressure; \(c_{{\text{p}}}\) = pore compressibility.

The pore compressibility is generally determined experimentally and assumes that the stress path followed by the reservoir during production is a priori known and constant. The usual stress paths in the reservoir are based on uniaxial or hydrostatic deformation conditions (Longuemare et al. 2002).

Geomechanical model

The governing equations for the geomechanical model are derived based on the balance of linear momentum and the effective stress law (Terzaghi, 1943), as follows in Eq. (9) to Eq. (12).

$$\nabla \cdot {{\boldsymbol{\upsigma}}} + {\mathbf{b}} = 0$$
(9)
$${{\boldsymbol{\upsigma}}} = {{\boldsymbol{\upsigma}}}^{{\mathbf{^{\prime}}}} + \alpha {{\boldsymbol{\updelta}}}p$$
(10)
$${{\boldsymbol{\upsigma}}} = {\mathbf{D}}:{{\boldsymbol{\upvarepsilon}}}$$
(11)
$${{\boldsymbol{\upvarepsilon}}} = \frac{1}{2}\left( {\nabla {\mathbf{u}} + \nabla^{{\text{T}}} {\mathbf{u}}} \right)$$
(12)

where \({{\boldsymbol{\upsigma}}}^{{\mathbf{^{\prime}}}}\) = effective stress tensor; \({{\boldsymbol{\upvarepsilon}}}\) = strain tensor; \({{\boldsymbol{\updelta}}}\) = Kronecker delta; \({\mathbf{b}}\) = body force; \({\mathbf{u}}\) = displacement vector; \(p\) = pore pressure (\(p = S_{{\text{o}}} p_{{\text{o}}} + S_{{\text{g}}} p_{g} + S_{{\text{w}}} p_{{\text{w}}}\)); \({\mathbf{D}}\) = constitutive tensor; \(\alpha\) = Biot’s coefficient.

To obtain the numerical solutions for Eqs. (1–3) and for Eqs. (9–12) normally it is used finite difference and Galerkin finite element methods, respectively. The flow model forecasts the pressure and saturation evolution in time and space, while the geomechanical model predicts the system's stress–strain behavior.

The coupling of the flow and rock mechanics equations is primarily by the volumetric change of porous rock due to pressure variation. The volumetric change relates directly to the strain and influences the flow equations through the porosity and permeability change. Especially for weak rocks, volumetric changes can have a great impact on these two parameters (Pettersen, 2012).

Methodology

The IMEX2MATLAB stress-dependent reservoir simulator consists of two-way explicit partial coupling of the commercial software Imex® for flow simulation and an in-house finite element program in MATLAB® for the stress/displacement analysis.

In the two-way explicit partial coupling approach, the reservoir simulator conducts the fluid flow calculations at each time step while stress-displacement calculations are performed only on selected timesteps of the analysis. Calling the geomechanics module in every single time step unnecessarily increases the computational expenses without much gain in the solution accuracy (Haddad and Sepehrnoori 2017).

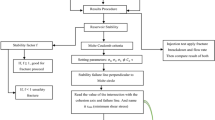
The coupled procedure solves the flow and mechanical problems separately for each time increment, as illustrated by the flowchart in Fig. 1. The flow equation solution provides the pressure and saturation distributions in the reservoir, while the geomechanical solution provides displacement, stress, and strain fields in the reservoir and adjacent regions because the stress changes and deformations propagate outside the porous domain. An interface module, also developed in MATLAB®, performs the automatic coupling procedure. This module is responsible for running the simulators in sequential order and for calculating/updating the coupling parameters between the two simulators at the specified time intervals.

Fig. 1
figure 1

Data exchange between flow and geomechanical model during the coupling. Where n is the total number of coupling timesteps

Full size image

The coupling procedure considers that changes in total stress are negligible, and that the pore pressure change induces an equal change, in modulus, in the effective stress. Thus, the pressure variation \(\Delta P\) results in an effective stress change expressed by Eq. (13).

$$\Delta {{\boldsymbol{\upsigma}}}^{{\mathbf{^{\prime}}}} = - \Delta P$$
(13)

Once Imex® has calculated the pressure change \(\Delta P\) in each grid block, the interface module will assign it to the corresponding nodes in the geomechanical mesh, according to Eq. (14) and Eq. (15). This data transfer depends on the discretization used for the flow and mechanical models. This study used coincident reservoir meshes, and the pressure change only generates normal stress.

$${{\boldsymbol{\upsigma}}}_{{\text{p}}}^{{\text{e}}} = [\begin{array}{*{20}c} {{\mathbf{dp}}^{{\text{e}}} } & {{\mathbf{dp}}^{{\text{e}}} } & {{\mathbf{dp}}^{{\text{e}}} } & 0 & 0 & 0 \\ \end{array} ]^{{\text{T}}}$$
(14)
$${\mathbf{F}}_{{\text{p}}} = \int\limits_{{\Omega_{{\text{e}}} }} {\mathbf{B}}^{{\text{T}}} {{\boldsymbol{\upsigma}}}_{{\text{p}}}^{{\text{e}}} {\text{ d}}\Omega_{{\text{e}}}$$
(15)

where \({{\boldsymbol{\upsigma}}}_{{\text{p}}}^{{\text{e}}}\) = pressure change tensor; \({\mathbf{dp}}^{{\text{e}}}\) = pressure change vector; \(\Omega_{{\text{e}}}\) = domain of the finite element e; \({\mathbf{B}}\) = Jacobian matrix of the finite element shape functions; \({\mathbf{F}}_{{\text{p}}}\) = nodal forces due to pressure change.

These nodal forces due to the pressure change are used to construct the global force vector of the mechanical problem in the Galerkin finite element formulation, as expressed in Eq. (16).

$${\mathbf{F}} = \int\limits_{{\Omega_{{\text{e}}} }} {\mathbf{N}}^{{\text{T}}} \rho {\mathbf{b}}{\text{ d}}\Omega_{e} + {\mathbf{F}}_{{\text{p}}}$$
(16)

where \({\mathbf{F}}\) = global force vector; \(\rho\) = density of the medium; \({\mathbf{N}}\) = matrix of finite element shape functions.

A new global force vector is calculated at each coupling time step by rewriting the corresponding input data files of the mechanical program in MATLAB®. The displacement field is determined by solving the system of equation described by Eq. (17), using the conjugate gradient method.

$${\mathbf{Ku}} = {\mathbf{F}}$$
(17)

where \({\mathbf{K}}\) = global stiffness matrix; \({\mathbf{u}}\) = displacement vector.

The global stiffness matrix, which contains information about the mesh structure and mechanical properties, is described by Eq. (18).

$${\mathbf{K}} = \int\limits_{{\Omega_{{\text{e}}} }} {\mathbf{B}}^{\text{T}} {\mathbf{DB}}{\text{ d}}\Omega_{{\text{e}}}$$
(18)

The displacements and stress/strain fields calculated are used to compute the coupling parameters of the flow formulation (i.e., pore compressibility, porosity, and absolute permeability).

Then, the interface module calculates the new pore compressibility and porosity as a function of pressure and volumetric strain by Eq. (19) and Eq. (20) (Inoue and Fontoura 2009a).

$$c_{{\text{p}}} = \frac{{\Delta \varepsilon_{{\upnu }} }}{{\phi_{0} \Delta p}}$$
(19)
$$\phi = \phi_{0} [1 + c_{{\text{p}}} (p - p_{0} )]$$
(20)

The absolute permeability change is correlated with the change in porosity by the porosity–permeability relationship in Eq. (21), developed by (Petunin et al., 2011).

$$K = K_{0} \left( {\frac{\phi }{{\phi_{0} }}} \right)^{n}$$
(21)

where \(\Delta \varepsilon_{{\upnu }}\) = volumetric strain; \(\phi_{0}\) = initial porosity; \(p_{0}\) = reference pressure; \(K_{0}\) = initial absolute permeability.

Thus, this methodology allows coupling the commercial reservoir simulator Imex® with a geomechanical module without any modifications to its source code by rewriting the permeability and pore compressibility input files during the flow simulation.

Verification of IMEX2MATLAB coupling procedure

For some comparative studies conducted, the results obtained from the numerical procedure shown in this article agree well with the fully coupled numerical solution.

The validation case is available in Dean et al. (2006) and consists of the depletion of a box-shaped reservoir contained within a stiff non-pay region. It is a single-phase flow problem with a production well in the center of the reservoir. The bottom and sides of the grid have zero normal displacement constraints, and all faces of the grid have zero tangential stresses. Table 1 summarizes the general properties of this problem, and Fig. 2 illustrates the model discretization. Geomechanical analyses were performed in 38 steps, with a time step size of 20 days for the first 400 days, followed by timesteps of 200 days, stopping at 4000 days.

Table 1 General information about Dean’s problem
Full size table
Fig. 2
figure 2

A Geomechanical mesh; B location of the reservoir in the geomechanical model

Full size image

The results of the IMEX2MATLAB partial coupling are checked against the explicit coupling solution by Dean et al.,(2006) for this problem. Figure 3 shows the average pressure in the reservoir, the vertical displacement at the top of the reservoir (compaction) and surface (subsidence) over time. The IMEX2MATLAB-coupling results are in close agreement with the published reference, indicating good quality of the implementation performed.

Fig. 3
figure 3

Validation case: A average reservoir pressure; B vertical displacement in the reservoir’s center block; C Vertical displacement in the surface’s center block

Full size image

Application

In this study, our emphasis is to quantify the impact of stress change on porosity and permeability and the resulting consequences on reservoir production. For each coupled simulation run, a corresponding simulation run with stress-insensitive permeability (K = K0) was also conducted to establish a quantitative comparison. Note that in both cases compaction effects are taken into account.

The simulations were performed to the Namorado Field (Campos Basin, Brazil), which is a sandstone reservoir. The reservoir model consists of 83*45*23 (I, J, K) cells, with 31,547 active cells (Fig. 4A). The geomechanical model extends beyond the reservoir because the stress change and deformations propagate outside the porous domain. This model was built by adding overburden to the surface, sideburden (rocks surrounding the reservoir laterally) and underburden to the reservoir model (Fig. 4B). The final geomechanical model size is 103*65*56 (I, J, K) hexahedral finite elements.

Fig. 4
figure 4

View of the model under study: A Reservoir finite difference grid and well location; B finite element mesh of the geomechanical model; C location of the reservoir in the geomechanical model

Full size image

Figures 5 and 6 illustrate the initial distribution of porosity and absolute permeability in the reservoir simulation model. These petrophysical properties have a heterogeneous distribution with an average of 20% for porosity, 336-mD, and 39-mD for horizontal and vertical permeability, respectively.

Fig. 5
figure 5

Porosity distribution in the reservoir model

Full size image
Fig. 6
figure 6

Absolute permeability distribution in the reservoir model: A horizontal [mD]; B vertical [mD]

Full size image

Figure 7 displays the mechanical properties in the geomechanical model. Young’s modulus and Poisson’s ratio vary by layer so that the stiffness increases with depth. The reservoir has values of 4 GPa and 0.33 for Young’s modulus and Poisson’s ratio, respectively. All analyses performed in this study considered linear elasticity applying boundary conditions of zero normal displacements in the bottom and sides of the grid.

Fig. 7
figure 7

Mechanical properties distribution: A Poisson’s ratio; B Young’s modulus [MPa]

Full size image

The reservoir fluid behavior uses the black oil formulation. Table 2 summarizes the reservoir properties. The model has nine producer wells and six injector wells. Producer “P-001” and injector “I-001” are vertical, and the rest are horizontal, as shown in the finite difference grid presented in Fig. 4A. Moreover, the natural mechanism acting is solution gas.

Table 2 Reservoir data
Full size table

Table 3 presents the operational constraints adopted in all simulation runs for twenty-seven years of production. Geomechanical analyses were performed in 12 steps, in which smaller timesteps are used at the beginning of the run and looser time-stepping for the following years (Table 4). Sensitivity analyses were performed to define these intervals of coupling.

Table 3 Operational constraints
Full size table
Table 4 Geomechanical coupling timesteps
Full size table

Different production scenarios in terms of primary and secondary drive mechanisms were evaluated. In the first analysis, we disabled the injector wells to assess the reservoir deformation impact under primary recovery. Then, we modified the bubble pressure to 5 MPa (683 psi) to evaluate the geomechanical effects without the presence of gas in reservoir conditions. Lastly, we analyzed secondary recovery.

We also performed some sensitivity analyses to assess the impact of different factors on the reservoir deformation and behavior (Table 5). The Young’s modulus of the reservoir adjacent rocks remains as illustrated in Fig. 7.

Table 5 Sensitivity parameters
Full size table

We compared the results from the coupled analyses with those from conventional flow simulation, which uses a constant pore compressibility value (Table 6). We calculated the equivalent constant pore compressibility according to Young’s modulus and Poisson’s ratio of the reservoir using Eq. (22) (Serra De Souza and Lima Falcão, 2015).

$$c_{{p_{{_{CONS} }} }} = \frac{(1 + \nu )(1 - 2\nu )}{{E(1 - \nu )}}$$
(22)

where \(\nu\) = Poisson’s ratio; \(E\) = Young’s modulus.

Table 6 Constant pore compressibility values for the conventional simulation
Full size table

Results and discussion

The following subsections discuss the results of the analyses to demonstrate the capability of the coupling procedure to incorporate geomechanics into the reservoir simulation. Besides, it is also possible to understand the impact of stress/strain change on reservoir properties, such as permeability and porosity, and its impact on production.

Primary recovery

The compaction that occurred in the reservoir affected not only its properties but also the overburden and underburden. As the reservoir compacts, it will pull down the overburden and pull up the underburden. Figure 8 illustrates the vertical displacement of the geomechanical model at the end of the simulation period. The largest displacements are located in the region where the producing wells are concentrated (Fig. 8B). The overburden tends to smooth the downward movement induced by reservoir compaction and gives smooth subsidence contours around the reservoir center, as illustrated in Fig. 8C, D.

Fig. 8
figure 8

Vertical displacement of the geomechanical model at the end of the simulation for Young’s modulus of 1 GPa and n = 0: A surface; B reservoir top; C XZ plane; D YZ plane

Full size image

Figure 9 shows the vertical displacement obtained for different reservoir stiffness. All other input data values are kept the same, as shown in Tables 2, 3 and 4. The simulated production activities led to the compaction of the reservoir, which in turn induced subsidence. As expected, the displacement is sensitive to reservoir stiffness. For Young's modulus of 1 GPa, compaction reached almost 2 m and subsidence almost 1 m after 27 years of production. For Young's modulus of 4 GPa, compaction reached no more than 0.5 m. The impact of these deformations on fluid recovery will be discussed.

Fig. 9
figure 9

Vertical displacement for different Young’s modulus of the reservoir (primary recovery and n = 0): A in the center of the reservoir top; B in the center of the surface

Full size image

Figure 10 displays the porosity variation profile on producer well “P-001” for conventional and coupled reservoir simulations. The porosity variation in the conventional simulation is negligible for all cases analyzed. In the coupled analyses, this variation is more pronounced once pore compressibility was updated during simulation according to volumetric deformation of the media. For Young’s modulus of 1 GPa, at the end of the simulation was observed a porosity average of 0.2046 and 0.1853 for the conventional and coupled simulations, respectively, and a difference of 9.4% between them. However, for Young’s modulus of 4 GPa, this difference is only 1.4%.

Fig. 10
figure 10

Porosity variation profile on producer well “P-001” for different reservoir stiffness: A Coupled simulation (n = 0); B conventional simulation

Full size image

Therefore, reservoir stiffness could be one of the parameters used to assist in the decision of whether a coupled analysis is important or not.

As shown in Fig. 11, the lower the reservoir stiffness, the more the results obtained from conventional simulation differ from those of the coupled analysis. The traditional update formulation of the porosity based on the constant equivalent compressibility under-estimates the fluid recovery. Under the same production scenario, the lower reservoir stiffness gives higher oil recovery. These results indicate the potential of reservoir compaction as a recovery mechanism and highlight the production-forecasting errors that can be made when stress-sensitive reservoirs are developed without considering geomechanical effects related to the pressure variation.

Fig. 11
figure 11

Impact of reservoir stiffness on fluid recovery (n = 15 for the permeability update law): A gas–oil ratio; B oil recovery factor; C gas recovery factor

Full size image

We can also see that the biggest difference between the coupled analyses with and without updating permeability is also with the decrease of reservoir stiffness since the porosity decreases more and directly affects the permeability. The gas–oil ratio (GOR) curve (Fig. 11A) shows that the permeability update slows down the production of the gas phase present in the reservoir conditions. The GOR decrease can contribute to the production of the oil since the permanence of the gas in the reservoir contributes to maintaining its pressure.

As illustrated in Fig. 11, the permeability change affects the productivity of the reservoir. It is well-known that reservoir compaction is a mechanism that could improve fluid recovery. However, depending on the sensibility of the permeability to this compaction, permeability can be greatly reduced and negatively affect oil production. So, the porosity–permeability relationship employed in the coupled analyses was analyzed. Figure 12 displays the production according to the exponent “n” used for permeability law (Eq. 21).

Fig. 12
figure 12

Impact of permeability law on fluid recovery for different reservoir stiffness: A Gas–oil ratio; B oil recovery factor; C gas recovery factor

Full size image

Depending on how strong is the coupling between the porosity and permeability, i.e., as exponent “n” increases, the greater is the effect on oil production. In this case, the reservoir pressure reaches the bubble pressure and a gas phase is formed in the reservoir conditions. It is possible to see that permeability reduction also affects the gas flow in the reservoir, reducing the mobility and production of this fluid, as can be seen in the GOR curve (Fig. 12A). Once the gas is the primary source of energy, this contributes to maintaining reservoir pressure and oil production. For Young's modulus of 2, 3, and 4 GPa, the final oil recovery in the coupled analyses updating permeability is the largest for all analyzed exponents. For the 1 GPa case, the final oil recovery depends on the exponent.

Depending on the reservoir stiffness and porosity–permeability relationship, permeability variation can increase or decrease oil recovery.

Figure 13 displays the horizontal permeability variation profile on producer well “P-001” for the different exponents “n” of the coupling permeability law. As the reservoir stiffness decreases and the exponent “n” increases, a large reduction in permeability can be observed throughout this well. For Young's modulus of 1 GPa and n = 30, at the end of the simulation was observed a permeability average of 48.8 mD, which means a reduction of 86.7%. However, for Young’s modulus of 4 GPa and n = 3, this reduction is only 5%.

Fig. 13
figure 13

Horizontal permeability variation profile on producer well “P-001”: A 1 GPa; B 2 GPa; C 3 GPa; D 4 GPa

Full size image

Figure 14 illustrates the distribution of porosity and the absolute permeability at the end of the simulation for the most stress-sensitive case of those analyzed. Horizontal and vertical permeability reached an average of 44 mD and 5 mD, respectively, while the average porosity was 0.187. Compared with the initial distribution (Fig. 5 and Fig. 6), there is an average reduction of 87% for the absolute permeability and 6.5% for the porosity in this case.

Fig. 14
figure 14

Porosity and absolute permeability distribution in the reservoir at the end of the simulation for Young’s modulus of 1 GPa and n = 30: A horizontal [mD]; B vertical [mD]; C porosity

Full size image

Thus, these analyses highlight the importance of laboratory tests to derive porosity–permeability relationships that apply to each field studied, to be used in the coupled simulations.

Figure 15A shows the fluid recovery for the modified value of bubble pressure (5 MPa) to evaluate the geomechanical effects without the presence of the gas phase in reservoir conditions. Here, the pressure remains above the bubble pressure and the only primary recovery mechanisms acting are reservoir compaction and oil expansion. It can be seen as a considerable difference between the results of the conventional and coupled reservoir simulations, once compaction is the main recovery mechanism in this case. For Young’s modulus of 1 GPa, there is a difference of 4.7% in oil recovery between these approaches. Besides, coupled analyses with and without updating the permeability showed close results.

Fig. 15
figure 15

Impact of reservoir stiffness on fluid recovery (no gas phase in reservoir, n = 15 for the permeability update law): A oil recovery factor; B pore volume

Full size image

Thus, for reservoirs producing above bubble pressure and which still have no secondary recovery method, the pore volume variation (Fig. 15B) can play an important role in fluid recovery.

Secondary recovery

Figure 16 shows the results of the coupled analyses for different reservoir stiffness and n = 0. Depletion is small due to the waterflooding, reaching no more than an average of 5 MPa (Fig. 16C). Therefore, the reservoir deformation magnitude is restricted. As illustrated in Fig. 16A, compaction reached no more than 0.45 m for the most stress-sensitive case. A recovery from deformation due to maintenance of pressure is observed, showing the elastic nature of the rock.

Fig. 16
figure 16

Results for different reservoir stiffness and n = 0: A vertical displacement in the center of the reservoir top; B vertical displacement in the center of the surface; C average reservoir pressure; D oil recovery factor

Full size image

For this case, the reservoir stiffness has no impact on oil recovery (Fig. 16D) because the pressure variation is tiny. Consequently, the compaction-induced porosity reduction is low, as shown in Fig. 17. Thus, maintaining pressure through fluid injection can be a good manner to mitigate geomechanical effects even in stress-sensitive reservoirs.

Fig. 17
figure 17

Porosity variation profile on producer well “P-001” for different reservoir stiffness: A coupled simulation; B conventional simulation

Full size image

Figure 18 compares the results from the conventional simulation and the coupled analyses with and without updating permeability. As shown in this figure, the difference between the simulations is negligible for all reservoir stiffness studied. So, for this production strategy, the conventional reservoir simulation can be satisfactorily used to predict the behavior of the reservoir.

Fig. 18
figure 18

Comparison of conventional and coupled results (secondary recovery, n = 15 for the permeability update law): A oil recovery factor; B water cut

Full size image

For the most stress-sensitive case (1 GPa and n = 15), horizontal and vertical permeability reached an average of 289.4 mD and 33.3 mD, respectively, while the average porosity was 0.198. Compared with the initial distribution, the maximum variation for the permeability and porosity reached 14% and 1%, respectively.

Therefore, the pressure variation magnitude could be another parameter used to assist in the decision of using coupled analyses.

Conclusions

In this article, an automated two-way partially coupled geomechanical reservoir simulator was used to investigate the impact of porosity/permeability changes in fluid recovery.

For the primary recovery scenarios analyzed, it was observed a significant difference in the results from the conventional and coupled reservoir simulations, mainly from the decrease in reservoir stiffness.

For the scenarios producing below the bubble pressure, permeability update slowed the production of the gas phase present in the reservoir conditions. The main finding is that depending on the reservoir stiffness and porosity–permeability relationship, permeability variation can increase or decrease oil recovery.

For the secondary recovery scenarios analyzed, it was observed no difference in the results from the conventional and coupled reservoir simulations due to the tiny pressure variation, and consequently little porosity/permeability changes. So, the conventional reservoir simulation could satisfactorily predict the behavior of the reservoir under this production scenario.

Based on the cases studied, the coupled analyses predicted higher oil recovery than conventional simulations. Therefore, if reservoir deformation is not taken into account in reservoir simulation, this could have a huge impact on history match and oil production forecast for stress-sensitive reservoirs.

The results show that compaction and subsidence evolution are strongly affected by both the drive mechanism (primary, secondary) and geomechanical characterization (Young’s modulus). Therefore, the pressure variation magnitude, the reservoir stiffness, and the porosity–permeability relationship could be parameters used to assist in the decision of using coupled analyses or not.

Lastly, this work also highlights the importance of laboratory analyses to identify the coupling law, which describes the petrophysical parameters variation concerning pressure/deformation. Rock mechanical properties directly affect petroleum production, showing the importance of estimating an accurate geomechanical model.