Analysis of permeability based on petrophysical logs: comparison between heuristic numerical and analytical methods

Abstract

A series of novel heuristic numerical tools were adopted to tackle the setback of permeability estimation in carbonate reservoirs compared to the classical methods. To that end, a comprehensive data set of petrophysical data including core and log in two wells was situated in Marun Oil Field. Both wells, Well#1 and Well#2, were completed in the Bangestan reservoir, having a broad diversity of carbonate facies. In the light of high Lorenz coefficients, 0.762 and 0.75 in Well#1 and Well#2, respectively, an extensive heterogeneity has been expected in reservoir properties, namely permeability. Despite Well#1, Well#2 was used as a blinded well, which had no influence on model learning and just contributed to assess the validation of the proposed model. An HFU model with the aim of discerning the sophistication of permeability and net porosity interrelation has been developed in the framework of Amaefule’s technique which has been modified by newly introduced classification and clustering conceptions. Eventually, seven distinct pore geometrical units have been distinguished through implementing the hybridized genetic algorithm and k-means algorithm. Furthermore, a K-nearest neighbors (KNN) algorithm has been carried out to divide log data into the flow units and assigns them to the pre-identified FZI values. Besides, a cross between the ε-SVR model, a supervised learning machine, and the Harmony Search algorithm has been used to estimate directly permeability. To select the optimum combination of the involved logging parameters in the ε-SVR model and reduce the dimensionality problem, a principle component analysis (PCA) has been implemented on Well#1 data set. The result of PCA illustrates parameters, such as permeability, the transit time of sonic wave, resistivity of the unflashed zone, neutron porosity, photoelectric index, spectral gamma-ray, and bulk density, which possess the highest correlation coefficient with first derived PC. In line with previous studies, the findings will be compared with empirical methods, Coates–Dumanior, and Timur methods, which both have been launched into these wells. Overall, it is obvious to conclude that the ε -SVR model is undeniably the superior method with the lowest mean square error, nearly 4.91, and the highest R-squared of approximately 0.721. On the contrary, the transform relationship of porosity and permeability has remarkably the worst results in comparison with other models in error (MSE) and accuracy (R²) of 128.73 and 0.116, respectively.

Introduction

Interesting to understand the flow mechanism of fluid in porous media is not particularly a novel field of study and has been studied for many years, but it has always been a challenging issue in heterogeneous carbonaceous reservoirs. Permeability is a pivotal parameter in fluid transmissibility researches and reservoir characterization. In general speaking, in situ measurement of permeability such as core analysis is impractical for all holes because it requires an immense deal of budget and back-breaking labor. Although nuclear magnetic resonance analysis (Diagle and Dugan 2011) and dipole acoustic log interpretation (Xiao 2013) are both rigorous methods and are conducted commonly to infer that, a challenge that arises in this domain is that their operation is not commercial. Consequently, the client companies would prefer to run them only in a special case. Selecting proper well-log attributes and being calibrated with core data is always the least expensive method to estimate the permeability profile (Johnson 1994).

A lot of attempts have been conducted to perceive the complexity of the permeability distribution into an all-inclusive practical model in which the significant problem is poor accuracy. The majority of prior researches had been applied based on Kozeny–Carman (Carman 1939). Needless to say, the Kozeny–Carman model is a successful predictable model, particularly homogenous porous media such as packs of uniform shape spheres (Wong 2003). One concern about the findings of Kozeny was, however, not just does it get an impression of grain size; but sorting, packing, and cementing as well are of the same level of importance that must be taken into account (Delhomme 2007). Coates–Dumanior (are well-known methods that are used frequently in petrophysical analysis to estimate permeability.

Equation 1 (Coats and Dumanior 1974) and Timur (Timur 1968) (Eq. 4) are well-known methods that are used frequently in petrophysical analysis to estimate permeability.

$$k^{\frac{1}{2}} = \frac{C}{{w^{4} }}\frac{{\varphi^{2w} }}{{{\raise0.7ex\hbox{${R_{w} }$} \!\mathord{\left/ {\vphantom {{R_{w} } {R_{t} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{t} }$}}}}$$

(1)

where w and C could be resulted from Eq. 2 and Eq. 3, respectively.

$$C = 23 + 465\rho_{h} - 188\rho_{h}^{2}$$

(2)

$$w^{2} = \left( {3.75 - \varphi } \right) + \frac{1}{2}\left[ {\log_{10} \left( {\frac{{R_{w} }}{{R_{t} }}} \right) + 2.2} \right]^{2}$$

(3)

$$k = A\frac{{\varphi^{B} }}{{S_{wi}^{C} }}$$

(4)

The major problem is the fact that those do not explicitly include the role played by the throat attribute. Not only the equations are poorly correlated in reservoirs with a large quantity of complexity, but the pore spatial structure is also not taken into account. As a matter of fact, none of these empirical models are realistically accounting for the constituent morphology of carbonate rocks, which leads to inadequate accuracy of permeability estimation (Delhomme, 2007).

Hydraulic flow unit (HFU) is a well-recognized definition which directly derived from the Kozeny–Carman equation and being used for some time to specify some rock fabrics based on their flow properties. It seemingly fills the gap resulted from the lacking of the pore shape meaning. HFU, as a classical method, is expressed to classify rock texture into different groups based on log attributes and core data. Seminal literature has been made based on the concept of hydraulic units (Corbett and Potter 2004). The principal addressable deficiency with this method is probably the need to correlate with petrography data, which sometimes is absent.

A closer investigation of the literature on empirical models, however, reveals gaps and shortcomings, because modeling the permeability of a heterogeneous carbonate reservoir requires analysis of all available data sources (Babadagli and Al-Salmi 2002). A new field of research, data mining, could help us to understand more precisely the major tenets required in permeability modeling. Extensive published works have been done in the soft computing implementation, such as fuzzy neural network in permeability estimation (Huang et al. 1996; Ali and Chawathe 2000), and (Shokir et al. 2006), fuzzy c means clustering technique for rock type (Ilkchi et al. 2006) support vector machine for predicting the permeability (Gholami et al. 2012), committee machine for permeability prediction (Chen and Lin 2006), and ANFIS in permeability prediction (Failed 2000).

The main purpose of the paper is a comparison between the commonly used empirical method of permeability estimation and the soft computing methods to generate more precise results. To that end, a state-of-the-art computer-based intelligent system needs to be implemented in a restricted area of study.

A further method to improve estimation and catch the casual relationships in rock properties is the implementation of soft computing method algorithms. In that research, a hybrid of harmony search and support vector regression machine learning is used to minimize the leak of knowledge.

Methods

Geological setting

Sarvak Formation, as a gigantic reservoir rock with more than 1200 m with a wide range of distinct carbonate successions in Marun Oil Field, south-west of Iran, has been conducted in the present research. Sarvak is a member of Bangestan group deposited in the Cretaceous Period and is predominately constituted from dolomitized calcite that most likely contains hydrocarbons in its porous media. This formation shows a much low gamma-ray reading, which is evidently an indicator of pay zone. Sarvak Formation has seven distinguishable subzones based on rock properties and geological deposition basin. The top three zones of the formation consist of wide-ranging fabrics including grainstone, packstone, and partial wackestone in some intervals, with fine to medium size foraminifera, which is of the highest productivity rate through intervals with reservoir properties. Owning fractures and vugs in carbonate rock’s framework by and large leads to have a sophisticated connection pathway between pore spaces. There is no doubt that this unpredictable pore size distribution affects the production regime and permeability magnitude. As the result, estimation of permeability in Sarvak Formation is turned into a problematic procedure in reservoir engineering.

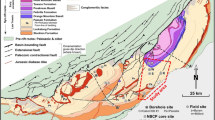
In this study, a collection of conventional petrophysical logging data and special core analysis (SCAL) is available in two different vertical wells (Well#1 and Well#2). As shown in Fig. 1, Well#1 is located in the north-west plunge of the anticline, and Well#2 lies in the crest of Marun Anticline. The contour map in Fig. 1 illustrates the top surface of Sarvak Formation, which is the zone of interest in this study. The entrance depth of Well#1 and Well#2 in Sarvak Formation is 3410 m and 3195 m, respectively. Data of Well#1 has been used as input data to train the models for that study. These data included all logging engineer parameters by which full petrophysical interpretation of porosity and water saturation is possible. Well#2 is also a blinded well that has no contribution in setting the models.

Fig. 1

Wells are disturbed in Marun Oil Fields. well#2 is situated in the north-west plunge of the anticline, and Well#1 is located in the crest of Marun longitudinal anticline

Heterogeneity analysis

Notwithstanding the fact that Sarvak Formation is uniformly formed in term of lithology, permeability and porosity distribution follows no obvious tendency. Such distribution, which is resulted from the reservoir heterogeneity in microscopic-scale, must be measured before taking any action. The fluctuation in the rock parameters is deeply dictated by the depositional environment, lithification, and diagenesis, such as dolomitization and stress-related events (Tiab and Donaldson 2016). As to quantify the level of the vertical reservoir heterogeneity, Craig (Failed 1971) published a statistical model to quantify the spatial heterogeneity of the reservoir parameters, which was named Lorenz coefficient. Lorenz coefficient can be valued between zero and one. Zero value of the Lorenz coefficient represents a homogenous reservoir. By contrast, the value of one is related to a completely heterogonous reservoir without any lucid tendency in petrophysical properties variations. That is to say, provided that the Lorenz curve is near a straight line with a unity slope, the reservoir is considered homogenous. Gunter et al. used Modified Lorenz Plot (MLP) to determine reservoir flow units (Gunter, et al. 1997) in a geological framework and split the reservoir into some homogenous subzones. In an exceedingly heterogeneous reservoir, the number of subzones increases, which leads to a decrease in the thickness of subzones. As a consequence, it would not be practical to use the MPL method in moderate to high heterogeneous reservoirs. So as to measure Lorenz coefficient, Flow Capacity (Eq. 5) and Storage Capacity (Eq. 6) were introduced in Eq. 5 and Eq. 6, respectively.

$$({\text{Flow}}\;{\text{Capacity}})_{j} = \frac{{k_{j} h_{j} }}{{\sum\limits_{i = 1}^{n} {k_{i} h_{i} } }}$$

(5)

$$({\text{Storage}}\;{\text{Capacity}})_{j} = \frac{{\varphi_{j} h_{j} }}{{\sum\limits_{i = 1}^{n} {\varphi_{i} h_{i} } }}$$

(6)

After sorting the core samples based on largeness of permeability (k) to porosity ratio values (φ) in descending, Flow Capacity and Storage Capacity are measured. The parameter of the thickness (h) is considered as a fixed value because of the same size of core samples. The following that, Cumulative Storage Capacity and Cumulative Flow Capacity were measured and plotted in a graph is shown in Fig. 2. Lorenz coefficient can be calculated as Eq. 7.

$${\text{Lk}} = \frac{{{\text{Area}}\,{\text{of}}\,{\text{ABCA}}}}{{{\text{Area}}\,{\text{of}}\,{\text{ADCA}}}}$$

(7)

Fig. 2

Lorenz Method to identify heterogeneity in Well#1

A hefty magnitude of the coefficient, 0.762, illustrates Sarvak Formation is a highly heterogonous reservoir that makes profound permeability changes vertically in Well#1. Under this condition, regression analysis and the Modified Lorenz Plot method will have a colossal potential to generate a high-degree of uncertainty in porosity–permeability correlation. It means both methods do not have sufficient eligibility to consider as a valid and reliable method to estimate permeability. Similarly, the Lorenz coefficient in Well#2 is measured at nearly 0.75, which means an extreme order of difficulty in reservoir characterization.

Permeability estimation by hydraulic flow unit

Amaefule and et al. (Failed 1993) introduced the Reservoir Quality Index parameter (RQI) with expanding Kozeny–Carman Equation, an equation that makes a physical link between porosity and permeability. They also introduced Flow Zone Indicator (FZI) which attributes the factors including the context of shape, tortuosity, and specific surface area. By referring Kozeny–Carman Equation (Carman 1939) in FZI calculation, if the core samples possess the same throat size and pore structure, they are supposed to be in a flow unit. FZI equation was developed by Amaefule as follows:

$${\text{FZI}} = \frac{{{\text{RQI}}}}{{\varphi_{z} }}$$

(8)

By and large, it is expected to refine the permeability relationship within each flow unit, if the borehole profile splits into some Hydraulic Flow Units (HFU). Following, these relationships can be applied to generate a continuous permeability profile along an uncored well. To identify the HFUs in Well#1, first of all, RQI and normalized porosity (φ_z) have been measured for each core sample in which absolute permeability and porosity have been obtained. By algebraically modifying Eq. 8 (taking algorithm from both sides), a robust mathematical explanation of HFU will be yield. Thereby plotting bi-logarithmically of RQI and φ_z, samples which place upon a straight line with a unit slope, will be assumed to have the same HFU with the same throat property. One important reason why hydraulic grouping is important is that it determines the number of patterns that must be modeled to estimate permeability (Johnson 1994). The average value of FZI can be calculated for each flow unit from the interception of the straight line in the unit normalized porosity. The number of these straight lines, which present the number of flow units (Doveton 2014), depends on the complexity of porous media. Identifying the number of flow units has a significant influence on HFU analysis since if that has not been considered enough, it is impossible to discriminate the same throat type in core FZI samples. Conversely, it seems as providing the number of HFUs units is overestimated, samples allocated to each flow unit will be reduced, and therefore, the constructed method behaves inaccurately because of high complexity. In this study, analyzing the error of the system, which has been designed by k-means method, has been implemented to reach the optimum number of FZIs.

k-means is an unsupervised, prototype, and non-heuristically clustering algorithm which simply splits a data set into a number of disjoint subsets. The subsets are specified with a centroid, and instances are assigned to clusters based on their similarities (Euclidean distance from their center of mass). So k-means is set to assume as an optimization problem to minimize the clustering error as an objective function. The major drawback of k-means is the high probability of trapping at a local optimum (Islam et al. 2014). Hybridizing k-means with an evolutionary search algorithm such as genetic algorithm could rise the chance of success in getting the global minimum of the sum of absolute clustering error. Genetic algorithm usage in optimization of clustering is fully described by Al Malki, et al. (Al Malki et al. 2016). Figure 3 represents a pseudo-code that simply depicts the procedure of the proposed Genetic k-means algorithm. The chromosome’s structure in the problem is coded as the position of the cluster’s center. The main genetic algorithm parameters which must be defined by the user are reported in Table 1. Crossover and mutation percentages are the parameters that define the proportion of the population that has to partake in the crossover and mutation process. The intensity of random alternation in the mutation process is dictated by the mutation rate. Gamma and selection rate are the parameters of the Roulette Wheel Selection algorithm which is commonly used in parent’s selection. The last but not the least parameter is the Maximum Count, which restricts the repetition in the converged result. Not only this parameter controls the processing time but also assists to escape from possible local extremums. The cost function to evaluate the eligibility of individuals in the genetic algorithm is coded based on the problem intrinsic. In the k-means problem, the cost function is the summation of inner cluster distances (Fig. 3).

Fig. 3

Pseudo code for Genetic k-means

Table 1 Parameters of models

The sum of absolute clustering error by increasing increment of flow unit numbers is illustrated in Fig. 4. As seen in Fig. 4, the sum of absolute clustering error decreased substantially by increasing the number of HFUs, but it was almost leveled off after 7. As a consequence, seven flow units have been considered as the optimum number.

Fig. 4

Sum Absolute Clustering Error resulted due a change in the number of HFUs

Each evaluated core sample has subsequently been allocated to a hypothetical flow unit by implementing the Genetic k-means method. As pictured in Fig. 5, the best fitted colored straight line passes throughout the points, in a bi-logarithmic plot of RQI versus φ_z in Well#1. Furthermore, the average of FZI in Fig. 5 has been extracted from interception of each straight line with y-axis and specified in Table 1.

Fig. 5

Determination of samples’ flow unit by k-means in Well#1

After separating core samples based on the identified HFUs, all uncored intervals ought to be divided into these seven classes. A way to identify the HFUs in uncored intervals is the classification with a meta-heuristic clustering method, namely KNN method. A KNN method, a supervised classification system, has been selected to divide intervals into prospered HFU based on log data. As documented by standard clustering textbooks (Larose 2005; Duda et al. 2000), the K-nearest neighborhood is an instance-based classification algorithm in use to produce some labels through the samples. These labels, C, are specified by evaluating the measurable likelihood dominant through the data set. Here, the measurable sampling is Euclidean distance. In brief, the KNN algorithm is ruled as follows:

• 1- Calculate all the Euclidean distance between each test set, Z, and training points, X.

• 2- Sort the distances in ascending order, and determine the k-nearest neighbor points to the points in Z.

• 3- Define the class of the points inside the set Z, based on the majority of k-nearest points.

Conventional well log data is often assumed to be available in each oil and gas drilled well. So that, it seems that integration of core and log data is required to make a bond between FZI and log attributes. To that end, the core data has been correlated in-depth with the log data as per gamma-ray readings. In this research, a matched point set of logging data from Halliburton Company’s tools including total gamma ray (KTH), spectral gamma ray (K, TH, U), resistivity (LLD and LLS), neutron (CN), density (ZDEN), photo-electron index (PE) and caliper reading (CALI), and core data including GR, porosity, and permeability, and predefine FZI from k-means in cored intervals has been imported into the KNN model. The number of k in the KNN algorithm is assumed to set 7 which equals the number of HFUs. At the end of the process, similar raw logging data along the uncored intervals has been run by the model as input parameters so to split the vertical profile of the wellbore into the related HFUs. The average FZI value of individual HFU has been used to estimate permeability from Eq. 9. The result of the whole intervals of Well#1 is depicted in Fig. 6. The colored bar in the right track represents the specified HFUs, which is addressed in the legend.

$$k = 1014\left( {{\text{FZI}}} \right)^{2} \left( {\frac{{\varphi^{3} }}{{\left( {1 - \varphi } \right)^{2} }}} \right)$$

(9)

Fig. 6

Estimated permeability from HFU model in Well#1

Input selection

Needless to say, input variable selection plays a major role in development of a precise model and reducing systematic errors. So as to select the best possible inputs, firstly it is crucial to identify whether an input is related to the output which here is permeability or is redundant. Roughly speaking, raising the number of input parameters does not assure the best performance of the model. For instance, as long as there is not an obvious relationship between inputs and output, it is likely to lead ultimately to a futile model. It should also be taken into consideration that raising the number of input variables might make the model more sophisticated to resolve (Wang and Chang 2006). Principal Component Analysis (PCA) has been used in Well#1 for aiming to conduct input variable selection. PCA is a dimensionality reduction method using eigenvalue to determine the meaningfulness of the variations (Failed 2013) and remove all redundant information before model training. As a consequence, it causes the model’s performance of the final model would be significantly upgraded (Wang and Chang 2006).

In PCA, all variables in a multi-dependency space will be summarized into a set of independent components (IC) that each IC has a linear combination of principal components (PC). PCs can be calculated from the eigenvector of covariance vector or correlation matrix of PCs. The first extracted PC has the highest level of distribution through the whole data set. This means the first PC correlates with some variables at least. More importantly, the second PC has two noticeable properties. Firstly, this principle takes into account the highest remained variation in the data. It means the second principle correlates with some variables, which have a high amount of discrepancy with the first PC. Secondly, the second PC has independence from the first one, and their dependency is zero. The other extracted components own both early mentioned properties for the second PC. PCA can be summed up into three sequential steps as follows:

• 1) Data normalization: The advantage of normalization is that it leads to removing the effect of scaling in the data. In the light of the fact that the covariance matrix, which is involved in PCA, is related to the scale of data measuring, the data in the original space should be normalized at the begging. In that study, all parameters have been normalized into a unit scale (zero mean and standard deviation of one).

• 2) Generate Covariance Matrix: Eigenvalue and eigenvector of the covariance matrix are the most influential elements in PCA. Eigenvector (PCs) identifies the directions of the new simplified feature space, and eigenvalues correspond to them. In other words, the eigenvalues identify the data variance in the direction of the feature axes. The applied formula to calculate covariance matrix is:

  $$\sum = \frac{1}{n - 1}((X - \mu )^{T} (X - \mu ))$$

  (10)

• 3) PCs Identification: As the aforementioned purpose of PCA, the dimension reduction of problem space is fulfilled by mapping the original space to a lower-dimension secondary space. In the secondary space, the eigenvector makes the coordinate exes. These eigenvectors only illustrate the direction of PCs, though, all their magnitudes equal unit. Finding the eigenvector including the lowest information, which certainly must be removed to make a less-dimension space, is a crucial step. Eigenvalue reveals how much data are varied in direction of corresponded eigenvector. To make the effort, eigenvectors have been sorted in descending order based on eigenvalues, that is to say, from the most weight to least, before anything else. Removing a component is associated with removing a part of information. Accordingly, the ignoring of inconsequential components should be done as precisely as possible.

The result of PCA is depicted in Fig. 7. Two first PCs contribute the lion’s share, just under 95 percent of variations, and the first PC has the overwhelming majority of overall variance, approximately a hefty 60 percent. The variance preparation of the second PC is merely one-third, whereas the proportion of third and fourth PC in overall variance is only 3.55 percent and 3.3 percent, respectively. Other principles have not been considered as PC, because of having partial contribution.

Fig. 7

Variance proportion to PCs in PCA

As regards PCs’ features, the correlation coefficient between input parameters and four PCs assists in all likelihood to investigate input parameter’s variation in more details. As seen in Table 2, all parameters have been categorized into four distinct groups according to the calculated correlation coefficient. The result of PCA shows parameters including permeability, sonic, deep resistivity, neutron, photoelectric index, spectral gamma-ray, and density own the highest amount of correlation coefficient with the first PC. Total gamma-ray, potassium, and thorium readings are more linked to the second PC. Also, Shallow resistivity and caliper log have the highest correlation coefficient magnitudes with the third and the fourth PCs, respectively. Therefore, all parameters, which are in the same group and correlated mostly with the first PC, have been selected as the inputs of the desired model.

Table 2 Average FZI value by k-means in Well#1

The performance of the model is evaluated by the error generated either during or after training; hence, the error is measured as a criterion to assess how well a model can measure the parameter of interest near the observed or real values. Testing error reflects the model responses, when a new set of data with no influence on the training phase is imported to the model. Moreover, comprehensibility is a major attribute that must be taken into account during the selection of the data set. In this case, 75 percent of core and log paired data set in Well#1 has been considered to train the model, and the remained 25 percent has been used as the testing data. Well#1 has the most intervals drilled in Sarvak Formation among all available wells. As a result, it is the best option to reach the highest possible comprehensibility of the model in the formation. After developing the model, the estimation error could be evaluated to show the ability of the model for unused data in previous steps. Well#2 is the blind well in which the data will be used to only check the validation of the model. Mean square error (MSE) and R-squared are two general parameters in model performance analysis (Hofer and Germany 2018), which have been used here.

ε -SVR model

The principle concept of support vector regression (SVR) is behind the attempt to sort out a function as a map to transform a set of input and output variables in such future space that they could be easily arranged in a linear trend (Failed 1997). As a matter of fact, SVR is a self-adjusting machine in which the map function parameters could tune to make a clear relationship through the data set. Hence, not only SVR might be a dimensionality reduction technique of the problem’s space, but it also solves the complex problem. However, there are some user-dependent parameters so-called hyperplane parameters including the width of the insensitive zone ε, regularization factor C, and the width of Gaussian Radial Basic Function (RBF) kernel λ. Unless hyperparameters (C, ε and λ) have been chosen by the optimization method, designing a good model is supposed to be an impractical achievement (Duda et al. 2000). Grid search is a commonly used technique to tune the proportional values for the separating hyperplane (Eitrich and Lang 2006). The dimension of grid search grows exponentially with the increasing configuration space, which ballooned the number of the function evaluation (Failed 2019). In the current research, a hybrid of SVR and Harmony Search has been innovated to cope with the setback of a possible imprecise prediction system. Harmony search has been confirmed by some researchers to optimize the critical parameters of ε-SVR in engineering problems (Dodangeha 2020)-(Fattahi 2016).

Harmony Search (HS), a metaheuristic algorithm, is conceptualized by Jazz musician’s improvisation to reach a perfect state of harmony (Zong Woo 2009). Pitch and harmony memory consideration rates are two fundamental meanings of this new stochastic random search method, which are inspired by the instrument’s improvisation process by musicians. The improvisation process is repeated several times and the best solution in harmony memory is selected as the final solution. To begin, the problem is defined to be solved by the harmony search that its parameters must be specified by the user. Table 3 provides the information on the HS algorithm’s parameters. In the next step, harmony memory is initialized randomly. Then, it starts to improvise and update the harmony memory by replacing better solutions. Ultimately, the stop criteria will be checked to decide that it must be ceased or the process needs to repeat.

Table 3 Result of PCA. The colors show how the input parameters are grouped to the PCs. Parameters with the highest correlation with the first PC have been selected to develop the ε-SVR model

All integrated inputs in the model have been normalized between zero and one to eliminate the effect of scaling on the model and develop the functionality of the kernel model. Well#1 includes 322 data points include SCAL and log data, which are divided randomly into two parts, training and resting as specified proportion. Figure 8 provides the details of the suggested structure for the ε -SVR model. The output of the ε -SVR method is a summation from the cross product of mapped vectors, which are resulted from the training data points (support vectors).

Fig. 8

Suggested structure for applied ε -SVR model

Hyperplane parameters (C, ε, and λ) have been determined by the HS algorithm to be 0.86, 1.052, and 3.01, respectively. While the MSE of training data had reached a rational amount of 0.48, the number of support vectors within the calculated margins of hyperplane (± ε) was 78, which is approximately 32 percent of whole training points. As long as the problem is complex, such a share of the support vectors is expected because of the complexity of the problem. Figure 9 depicts how correlation exists between target and output of the model in the testing part of data (75 percent of whole data). The distance between predicted and real data on the top section of the plot is more than those at the bottom section because of the logarithmic property of the plot. MSE and R² which have resulted in training data are 0.0023 and 0.961, respectively, and those in testing data, are 0.0041 and 0.941, respectively.

Fig. 9

Correlation plot of ε-SVR model for testing data

Result

Five numerical and analytical models have been implemented to study the permeability of Sarvak Reservoir in Marun Oil Field. Well#2 with the same data structure as Well#1 will be analyzed to compare the validation of the developed models. In Well#2, all intervals have been segmented into seven different HFUs in a similar way to Well#1. The KNN model, which was developed in Well#1, has been driven to implement the classification. Firstly, all input parameters consist of the caliper, spectral gamma ray, thorium and potassium, resistivity logs (deep and shallow), neutron porosity, density, sonic wave slowness, and photoelectric index. The intensive failure of the wellbore by which the logging tools are influenced must be determined and eliminated from the model. So, the 8-m interval of the top section of the open hole in Well#2 has been removed. Hence individual HFU has been assigned to an FZI value, and permeability has been calculated in depth by Eq. 9.

The methods of Coates–Dumanior (Equation 1) and Timur (Equation 4), which are the most generally used practical method in the traditional petrophysical analysis, have been candidates among the analytical methods. The salinity of the water content in Sarvak Formation was set to be 300,000 ppm. Oil’s API is experimentally measured 31. Moreover, both rock fabric-related parameters (cementation factor and saturation exponent) have been adjusted 2. Interpretation of the petrophysical logs shows there is no gas cap. After analyzing the petrophysical log, 0.26 has been considered as irreducible water saturation in Coates–Dumanior for Well#2. Consequently, the Coates–Dumanior coefficient (Equation 2) has been calculated at 400. The parameter of w, by considering porosity and water saturation, has been calculated (Equation 3) like a continuous curve. On the other hand, A, B, and C are unknown parameters in the Timur model which have been considered here, 100, 2.25, and 1, respectively.

Lastly, an ε-SVR, which trained in Well#1 by hybrid method of HS algorithm and support vector regression method, has been tested in Well#2. As determined by the PCA method, Neutron, Density, Sonic, LLD, PEF, SGR have been loaded as the inputs into the model, after normalizing them between zero and one. Figure 10 shows the predefined flow units in the blinded well, Well#2, on the scale of 1/200. The proper FZI value has been chosen to estimate permeability from the average FZI which is represented in Table 1. The used color map of HFUs in the figure is the same as the one in Fig. 6. What is more visible in Fig. 10 is that mostly determined HFUs are related to HFU 5 and HFU 6. Also, the estimated permeability from the FZI method in these flow units is ranged between 0.5 and 5 md. However, in an interval dominated by HFU 3 from 3281 to 3286 m, the permeability changes below 0.5 md. The second point is that the permeability of the Timur method follows the permeability of the Coates–Dumanior method. The transform method is not presented in Fig. 10, because of the high amount of error.

Fig. 10

Graph compares the estimated permeability from the utilized methods with core data in Well#2. The first left track is a presentation of the permeability of Timur and Coates–Dumanior methods. The second track is a profile of FZI method. The third track is a table of HFUs, and the fourth track is the permeability of ε-SVR model and porosity. The points are the permeability from the core

The regression plot shows how exactness the utilized models are. Line with 45-degree steepness is the criterion to judge the estimation accuracy. Providing the data points are as nearest as possible to the line, the accuracy of the studied model will increase. Figure 11 compares graphically the performance of the methods from the point of statistic. The reading of gamma-ray is pictured by a color map between 0 and 100. As expected, Sarvak Formation is formed from almost clean limestone with a low amount of natural gamma-ray radiation. Figure 11a is the histogram and the regression plot of the transform-relationship between porosity and permeability driven from the core and the logging data. The estimation is poorly correlated with the core data. As seen, the transform method fluctuates just around 1 md in most of the samples. It produces a high amount of positive error amount, which is because of a low estimated value of permeability. The normality distribution of the error is a manifestation to discern a random error from a systematic one. Figure 11b and c is the representation of the error distribution and the regression plot of the output in the Coates–Dumanior method and the Timur method, respectively. Definitely, both methods underestimate the permeable zones, whereas the Timur method overestimates more than the Coates–Dumanior method in impermeable zones. The non-normal distribution of error in both methods is a reason for the non-applicability of them for permeability estimation. The performance of the FZI model is depicted in Fig. 11d, which can be concluded that the method is moderately acceptable. The normal distribution of the FZI and the hybrid of HS and ε-SVR is in the consequence of randomly intrinsic of the calculated error. Figure 11e shows the more accurate estimation of the permeability in permeable and impermeable zones. The regression plot represents the close prediction of the actual data in the ε-SVR model.

Fig. 11

Histogram and regression plot compare the estimated permeability from the utilized methods with core data in Well#2, (a): Regression Method, (b): Coates–Dumanior Method(c): Timur Method, (d):FZI method, and (e) ε-SVR method

As shown clearly in Fig. 12, it reveals the fact that ε-SVR model is of a statistically significant improvement at all levels. The red bars are related to the error and the blue bars show the amount of accuracy. According to these results, ε-SVR is the model that must be undeniably the best with MSE and R² of 4.91 and 0.721, respectively. In contrast, the transform relationship of permeability and porosity has remarkably the worst results compared to other used models with error and accuracy of 128.73 and 0.116, respectively. As a matter of statistic, the FZI model has a modest result, with an R² of nearly 0.60 and an MSE of 7.12. Coates–Dumanior model has superiority compared to Timur model, but both models are not suggested for carbonate reservoirs with a complex porous media.

Fig. 12

Performance of the utilized models in permeability estimation

Conclusion

This paper reports a modeling procedure of permeability from petrophysical well logging data. We coded firstly two prior empirical methods investigated by Dumanior-Coates and Timur to measure depth-based permeability. Next, a new methodology was designed to use hydraulic flow unit (HFU) context including intelligent optimization method, genetic algorithm, and the numerical clustering k-means and the classification algorithm of KNN to make a map between core-scale reservoir, geological description, and well logging data. One limitation is that this method is strictly core-dependent and cannot be implemented for a new field case unless a desirable quantity of SCAL data set is supplied. One concern about the findings of the HFU technique was the lack of the result of mercury injection and/or centrifuge capillary pressure test or petrographic data to confirm its validation by comparing with.

Because of the lack of sonic full waveform and NMR data in well and core laboratories, it has been decided to not investigate the effect of these data on the result of the proposed model. However, one cannot argue against the fact that the dipole sonic and NMR data would increase the accuracy of the utilized model.

In this study, three kinds of procedures were implemented to estimate permeability in Sarvak Formation, a gigantic reservoir rocks through the world. By regarding the core analysis, the whole interval was divided into seven distinct hydraulic flow units. This affirmation can assign an average FZI to individuals of them to measure permeability. In that procedure, a hybrid of a k-means classification system and genetic algorithm plays a major role. However, noticeably, it is possible by investigating through another classification system, roughly better performance could be obtained. To expand the HFU definition from limited core samples to a continuously recorded log, KNN was applied. By knowing the average FZI for each depth, Amaefule introduced a method to calculate permeability based on the Kozeny–Carman method. As the relationship between permeability and petrophysical log parameters is extremely ambiguous, ε-SVR code was developed in such a way that a direct-mapping was constructed to simulate this relationship. Hyperplane parameters of ε-SVR were defined by the HS method. PCA was also used to clarify in which combination of log parameters, the best performance will have been obtained. In that case, neutron porosity, bulk density, compressional sonic transit time, formation resistivity, photo-electric index, and naturally scattered gamma-ray were the best combination. The results showed that the hybrid of ε-SVR and HS model had the best performance among all proposed models in that research. A benefit of the ε-SVR method is that there is no need to calculate porosity and water saturation degree, which has the potential to be a source of systematical error in the final results. Also, Coates–Dumanior model has superiority in comparison with the Timur model, but both models are not suggested for carbonate reservoirs with a complex porous media.