Introduction

The concept of tight oil can be divided into broad and narrow senses. Tight oil in a broad sense refers to the petroleum resources stored in tight reservoirs, and its development requires fracturing technology. Tight oil in a narrow sense refers to the petroleum resources stored in tight reservoirs other than shale, and its exploitation also requires fracturing technology. The broad concept of tight oil includes oil resources in shale reservoirs and emphasizes the tightness of the reservoirs. This paper mainly focuses on tight oil in a narrow sense.

Currently, the development of tight oil reservoirs largely depends on hydraulic fracturing technology. Through hydraulic fracturing, fractures can be built in vertical wells, which not only change the way of fluid seepage near the wellbore, but also expand the swept area in the process of oil reservoir exploitation and enhance oil recovery. Therefore, hydraulic fracturing technology has broad application prospects in tight oil reservoir development, and how the bottom hole pressure changes along with the fracturing process is of great importance for the tight oil exploitation.

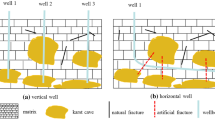
Formation pressure refers to the pressure acting on the fluid in the pore space of the rock in the reservoir formation, which reflects the energy in oil reservoir, and it is the driving force of the crude oil flow. In the oil reservoir development, bottom hole pressure is the most direct response to the formation pressure. Generally, there are two methods for obtaining pressure, one is direct measurement, and the other is indirect acquisition through well test, as shown in Fig. 1.

Fig. 1
figure 1

Summary of the methods used in well pressure measurement

Full size image

For the indirect method, many researchers focus on the analytical model. They have done a lot of researches on the unsteady flow pressure of fracturing vertical wells and have made great progress (Cai et al. 2008; Wang et al. 2014; Zhao et al. 2015; Liu 2016; Zhu et al. 2017; Shen et al. 2018; Jiang et al. 2019). However, previous classical methods still have limitations in the application and guidance of tight oil reservoir development. It is mainly showed as follows: (1) The seepage model is ideal and does not fully consider the crossflow between the fracture and matrix. (2) In order to obtain the solution to the pressure, some approximate treatments were made, which affected the accuracy of the results. (3) The derivation process is complicated, and the calculation is inconvenient. (4) Green's function is suitable for closed boundary reservoirs with considering the upper and lower boundaries, so the method has certain limitations (Ramey and Gringarten 1973; Ramey and Gringarten 1974).

We attempt to give some new insights in understanding the bottom hole pressure in a circular reservoir. This paper presents an analytical solution that describes pressure transient behavior for unsteady flow by considering the crossflow between the fracture and matrix, and it is successfully applied to examine effects of the fracture orientation, fracture half-length, elastic reservoir capacity ratio, exchange coefficient, skin factor and permeability ratio on performance of fracturing vertical well in a tight oil reservoir with closed boundaries based on pressure and pressure derivative concepts. More specifically, this paper uses Laplace transformation, axisymmetric transformation and similar methods, separation of variables to obtain the analytical solution of Laplace domain. Then, the Stephenson Numerical method (Stehfest 1970) was used to obtain the numerical solution in a real domain. The results agree with the numerical simulations and actual test data, suggesting this method is scientific and available. The advantage of the solution devotes to its efficiency and accuracy.

Mathematical model

Basing on production testing characteristics and well test analysis, it is recognized that the dual media reservoir has a linear flow after fracturing (Bourdet 1985; Liu 1993), that is, the fracture can stably supply fluid to the wellbore. To simplify the description of the subsurface fluid by the mathematical model, the following assumptions are made as below: (1) The fluid is a micro-compressible fluid with two media, namely matrix and fracture. (2) The crossflow between the matrix and the fracture is considered. (3) The gravity and capillary force are not taken into consideration. In the center of the reservoir, there is a fractured vertical well, as shown in Fig. 2. The diffusivity equation of the unsteady flow is given as follows:

$$\left\{ \begin{gathered} C_{m} \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}\left( {r_{D} \frac{{\partial p_{mD} }}{{\partial r_{D} }}} \right) = \omega_{m} \frac{{\partial p_{mD} }}{{\partial t_{D} }} + \zeta (p_{mD} - p_{fD} ) \hfill \\ C_{f} \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}\left( {r_{D} \frac{{\partial p_{fD} }}{{\partial r_{D} }}} \right) = \omega_{f} \frac{{\partial p_{fD} }}{{\partial t_{D} }} + \zeta (p_{fD} - p_{mD} ) \hfill \\ \end{gathered} \right.$$
(1)
Fig. 2
figure 2

Schematic diagram of multi-fracture vertical well reservoir

Full size image

Initial conditions:

$$p_{jD} (r_{D} ,0) = 0,\quad j = m,f$$
(2)

Boundary conditions:

$$\frac{{\partial p_{jD} (1,t_{D} )}}{{\partial t_{D} }} = 0,\quad j = m,f$$
(3)
$$\left( {C_{m} \frac{{\partial p_{mD} }}{{\partial r_{D} }} + C_{f} \frac{{\partial p_{fD} }}{{\partial r_{D} }}} \right)_{{r_{D} = 1}} = - \frac{1}{{L_{D} }} + \frac{1}{S}$$
(4)

where

Dimensionless coordinates: \(r_{D} = \frac{r}{{r_{w} }},\;L_{D} = \frac{L}{h}\).

Dimensionless pressure: \(p_{jD} = \frac{{2\pi h(k_{m} + k_{f} )}}{\mu q}(p_{i} - p_{j} ),\quad j = m,f\).

Dimensionless time: \(t_{D} = \frac{{t(k_{m} + k_{f} )}}{{r_{w}^{2} [(\phi \mu c_{t} h)_{m} + (\phi \mu c_{t} h)_{f} ]}}\).

Dimensionless flow coefficient:\(C_{m} = \frac{{k_{m} h_{m} }}{{k_{m} h_{m} + k_{f} h_{f} }},\;C_{f} = \frac{{k_{f} h_{f} }}{{k_{m} h_{m} + k_{f} h_{f} }}\).

Conversion factor of dual-medium fluid:\(\zeta = \alpha r_{w}^{2} \frac{{k_{m} h_{m} }}{{k_{m} h_{m} + k_{f} h_{f} }}.\)

Elastic storage capacity ratio:\(\omega_{m} = \frac{{\phi_{m} c_{tm} h_{m} }}{{\phi_{m} c_{tm} h_{m} + \phi_{f} c_{tf} h_{f} }},\omega_{f} = \frac{{\phi_{f} c_{tf} h_{f} }}{{\phi_{m} c_{tm} h_{m} + \phi_{f} c_{tf} h_{f} }}\).

\(r,r_{w}\) are the seepage radius and the wellbore radius, m.

\({\kern 1pt} L,h\) are the fracture half-length and the effective thickness of the reservoir, m.

\(k_{m} ,k_{f}\) are the permeability of matrix and fracture, μm2.

\(\mu\) is the fluid viscosity, mPa·s.

\(p_{m} ,p_{f}\) are the fluid pressure in the matrix and fracture, MPa.

\(h_{m} ,h_{f}\) are the effective thickness in the matrix and the fracture, m.

\(t\) is the production time, s.

\(q\) it the fluid production, m3/d.

\(c_{tm} ,c_{tf}\) are the compressibility of the matrix and the fracture, MPa−1.

\(\phi_{m} ,\phi_{f}\) are the porosity of matrix and fracture.

\(S\) is the skin factor.

The subscripts f and m represent fracture and matrix, respectively. Equations (1)–(4) constitute the instantaneous pressure mathematical model of the unsteady flow in a dual-medium fracturing vertical well.

Model solving

At present, there are mainly five methods to solve the unsteady flow seepage control equation. (1) The Green function: Without considering the propagation time of the seepage pressure, it is used to obtain the analytical solution of the diffusivity equation in the Laplace space domain (Feng and Ge 1985; Alpheus and Tiab 2008). (2) The steady-state successive replacement method (SSR): The pressure propagation radius is subdivided into multiple segments, and the pressure in each segment can be expressed as a function of time. SSR is used to obtain the numerical solution of the diffusion equation (Li and Liu 1997; Buhidmal and Raghavan 1980). (3) The numerical approximation algorithm: Basing on the series theory, it is used to obtain the numerical solution of the diffusion equation (Feng and Fu 1997; Liu et al. 2015). (4) The perturbation method: It is used to obtain the approximate solution of the diffusion equation in the case of constant production (Kale and Mattar 1980). (5) The Boltzmann transformation method: It is used to obtain the solution of the diffusion equation under the condition of constant production in an infinite reservoir (Peres et al. 1987).

The above five methods have a good effect on solving the self-similarity problem. However, there are still some limitations in solving the nonlinear seepage diffusion equation. The basis for obtaining bottom hole pressure is to solve diffusivity equation with the integration of axisymmetric transformation and similar methods, which is presented for the first time. Different from the traditional method of using the Green’s function and source solution, this paper uses Laplace transformation, axisymmetric transformation and similar methods, separation of variables to obtain the analytical solution of Laplace domain. Then, the Stephenson Numerical method was used to obtain the numerical solution in a real domain.

The Laplace transform of Eqs. (1)–(4) are

$$\left\{ \begin{gathered} C_{m} \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}\left( {r_{D} \frac{{\partial \overline{{p_{mD} }} }}{{\partial r_{D} }}} \right) = \omega_{m} s\overline{{p_{mD} }} + \zeta \left( {\overline{{p_{mD} }} - \overline{{p_{fD} }} } \right) \hfill \\ C_{f} \frac{1}{{r_{D} }}\frac{\partial }{{\partial r_{D} }}\left( {r_{D} \frac{{\partial \overline{{p_{fD} }} }}{{\partial r_{D} }}} \right) = \omega_{f} s\overline{{p_{fD} }} + \zeta \left( {\overline{{p_{fD} }} - \overline{{p_{mD} }} } \right) \hfill \\ \end{gathered} \right.$$
(5)

Initial conditions:

$$\overline{{p_{jD} }} (r_{D} ,0) = 0,\quad j = m,f$$
(6)

Boundary conditions:

$$s\overline{{p_{jD} }} = 0,\quad j = m,f$$
(7)
$$\left( {C_{m} \frac{{\partial \overline{{p_{mD} }} }}{{\partial r_{D} }} + C_{f} \frac{{\partial \overline{{p_{fD} }} }}{{\partial r_{D} }}} \right)_{{r_{D} = 1}} = - \frac{1}{{sL_{D} }}$$
(8)

According to the solution form of the axisymmetric two-dimensional seepage equation, suppose the solution of Eq. (5) is given as follows:

$$\left\{ \begin{gathered} \overline{{p_{mD} }} = Af(r_{D} ,\sigma ) \hfill \\ \overline{{p_{fD} }} = Bf(r_{D} ,\sigma ) \hfill \\ \end{gathered} \right.$$
(9)

where: \(R = \frac{{K_{0} (r_{D} \varepsilon_{0} )}}{{\varepsilon_{0} K_{1} (\varepsilon_{0} )}} + 2\sum\limits_{n = 1}^{x} {\frac{{K_{0} (r_{D} \varepsilon_{n} )}}{{\varepsilon_{n} K_{1} (\varepsilon_{n} )}}} \frac{{\sin (n\pi L_{D} )}}{{n\pi L_{D} }}\cos (n\pi r_{D} )\), \(q_{n} = \sqrt {\sigma^{2} + (n\pi )^{2} }\).

Substitute Eq. (9) into Eq. (5), and we can get:

$$\left\{ \begin{gathered} (C_{m} \sigma^{2} - \omega_{m} s)A + \lambda B = 0 \hfill \\ \lambda A + (C_{f} \sigma^{2} - \omega_{f} s)B = 0 \hfill \\ \end{gathered} \right.$$
(10)

Equation (10) has a solution, which must satisfy the following conditions:

$$\frac{{C_{m} \sigma^{2} - \omega_{m} s}}{\lambda } = \frac{\lambda }{{C_{f} \sigma^{2} - \omega_{f} s}}$$
(11)

Which is

$$\sigma ^{4} - s\left( {\frac{{\omega _{m} }}{{C_{m} }} + \frac{{\omega _{f} }}{{C_{f} }}} \right)\sigma ^{2} + \frac{{\omega _{m} \omega _{f} s^{2} - \lambda ^{2} }}{{C_{m} C_{f} }} = 0$$
(12)

The solution of Eq. (12) is given as follows:

$$\left\{ \begin{gathered} \sigma _{1}^{2} = \frac{1}{2}\left[ {s\left( {\frac{{\omega _{m} }}{{C_{m} }} + \frac{{\omega _{f} }}{{C_{f} }}} \right) + \sqrt {s^{2} \left( {\frac{{\omega _{m} }}{{C_{m} }} + \frac{{\omega _{f} }}{{C_{f} }}} \right)^{2} - 4\frac{{\omega _{m} \omega _{f} s^{2} - \lambda ^{2} }}{{C_{m} C_{f} }}} } \right] \hfill \\ \sigma _{2}^{2} = \frac{1}{2}\left[ {s\left( {\frac{{\omega _{m} }}{{C_{m} }} + \frac{{\omega _{f} }}{{C_{f} }}} \right) - \sqrt {s^{2} \left( {\frac{{\omega _{m} }}{{C_{m} }} + \frac{{\omega _{f} }}{{C_{f} }}} \right)^{2} - 4\frac{{\omega _{m} \omega _{f} s^{2} - \lambda ^{2} }}{{C_{m} C_{f} }}} } \right] \hfill \\ \end{gathered} \right.$$
(13)

Substitute Eq. (13) into Eq. (9), and we can get:

$$\left\{ \begin{gathered} \overline{{p_{mD} }} = a_{1} \frac{{1 - a_{1} }}{b}\overline{{R(\sigma_{2} )}} R_{1} (r_{D} ,\sigma_{1} ) + a_{2} \frac{{1 - a_{2} }}{b}\overline{{R(\sigma_{1} )}} R_{2} (r_{D} ,\sigma_{2} ) \hfill \\ \overline{{p_{fD} }} = \frac{{1 - a_{1} }}{b}\overline{{R(\sigma_{2} )}} R_{1} (r_{D} ,\sigma_{1} ) + \frac{{1 - a_{2} }}{b}\overline{{R(\sigma_{1} )}} R_{2} (r_{D} ,\sigma_{2} ) \hfill \\ \end{gathered} \right.$$
(14)

where:

$$a_{1} = 1{ + }\frac{{s\omega_{m} - C_{m} \sigma_{1}^{2} }}{\lambda },\; a_{2} = 1{ + }\frac{{s\omega_{f} - C_{f} \sigma_{2}^{2} }}{\lambda }$$
$$b = s[(C_{m} a_{2} + C_{f} )(1 - a_{1} )\overline{{R(\sigma_{1} )}} - (C_{f} a_{1} + C_{f} )(1 - a_{2} )\overline{{R(\sigma_{2} )}} ]$$
$$\overline{R(\sigma )} = \frac{{K_{0} (r_{D} \varepsilon_{0} )}}{{\varepsilon_{0} K_{1} (\varepsilon_{0} )}} + 2\sum\limits_{n = 1}^{ \propto } {\frac{{K_{0} (r_{D} \varepsilon_{n} )}}{{\varepsilon_{n} K_{1} (\varepsilon_{n} )}}} \frac{{\sin^{2} (n\pi L_{D} )}}{{(n\pi L_{D} )^{2} }}$$

According to Eq. (14), at the interface between fracture and matrix, the pressure is equal, and the analytical expression of bottom hole pressure can be solved as follows:

$$\overline{{p_{wD} (s)}} = \frac{{a_{2} - a_{1} }}{s}\left[ {\frac{{(a_{2} - 1)(C_{m} a_{1} + C_{f} )}}{{\overline{{R(\sigma_{1} )}} }} + \frac{{(a_{1} - 1)(C_{m} a_{2} + C_{f} )}}{{\overline{{R(\sigma_{1} )}} }}} \right]$$
(15)

Equation (15) is the analytical solution of the Laplace domain, and the pressure value in the real domain is obtained by Stehfest numerical inversion method (Stehfest 1970).

Model validation and analysis

Model validation

E300 simulation

The latest E300 module in the Eclipse2014 software is well applied in dual-medium heterogeneous reservoirs. This article uses this module to simulate bottom hole pressure. First, the oil reservoir is set as a circular reservoir, and there is a vertical well producing in the center of the reservoir. After hydraulic fracturing, 5 fractures are built, and they are all symmetrically distributed about the wellbore. The reservoir boundary has a constant pressure. In order to facilitate the description of the interaction between the fractures and the matrix around the wellbore, corner grids are used for grid division, and each fracture has at least three grids. The reservoir radius is 1000 m. The radial length step is 25 m, and the direction step is 10°. In the vertical direction, 5 simulation layers are planned, so the total number of grids is 40 × 36 × 5 = 7200 grids. The grid division diagram is shown in Fig. 3. The other required parameters are shown in Table 1. The solution of the E300 simulation and this paper is shown in Fig. 4. We can see a very good agreement between the solution in the E300 simulation and this paper, and the relative error is very small, indicating that the method used in this paper produces reliable bottom hole pressure.

Fig. 3
figure 3

Schematic diagram of the reservoir

Full size image
Table 1 Table of required parameters for calculation
Full size table
Fig. 4
figure 4

Comparison of the calculation results of the two methods

Full size image

The actual data

A new sweet spot was discovered in a tight oil reservoir in 2012 (Liu et al. 2012). After the well in the sweet spot center was hydraulically fractured, 24 fractures were built. Well tests showed that the sweet spot was approximately a circular reservoir. The reservoir radius is about 1932 m, and its effective thickness is 16.5 m. The bottom hole pressure was monitored during oil production. Based on the actual reservoir parameters, the model in this paper is used to calculate the bottom hole pressure, as shown in Fig. 5. Figure 5 shows that the two methods are in good agreement, indicating the validity and accuracy of this method.

Fig. 5
figure 5

Comparison of the calculation results and the actual data

Full size image

In summary, both show that the method used in this paper produces reliable bottom hole pressure.

Flow period division

By using Stehfest numerical inversion method to solve Eq. (15), the pressure values in the real domain were obtained, as shown in Fig. 6. Figure 6 shows that pressure curves can be divided into eight stages.

Fig. 6
figure 6

Pressure and pressure derivative curve

Full size image

Stage A: Early linear flow. The fluid in the wellbore flows to the wellhead. This stage is mainly affected by the wellbore storage effect, and the curve shows that the pressure and the derivative of the pressure coincide with each other. The slope of this curve section is 1.

Stage B: It is called a continuous flow transition section, and the fluid in the formation begins to flow into the wellbore.

Stage C: Fracture linear flow. The fluid in the fracture begins to flow into the wellbore.

Stage D: Formation linear flow. The fracture provides sufficient fluid, and Darcy seepage occurs in the reservoir.

Stage E: Crossflow. The fluid in the matrix begins to flow to the fracture, and the pressure derivative appears sag. This stage is an unsteady flow stage. Due to the interfacial flow between the fracture and the matrix, the seepage velocity of the fluid in the two media is obviously different, and the pressure derivative curve shows the trend of concave downward. The progressive analysis shows that the greater the permeability difference between fracture and matrix, the more obvious the tendency of pressure derivative curve is.

Stage F: Transitional flow. In this stage, the pressure derivative has a curved curve. If the fluidity in the fracturing unaffected area becomes better, the pressure derivative will drop. If the fluidity in the fracturing unaffected area becomes worse, the pressure derivative will rise.

Stage G: Pseudo-radial flow. The flow between the fracturing affected areas and unaffected areas reaches a pseudo-steady state. The pressure curve is 1 when the system is in quasi-steady state.

Stage H: The boundary control flow. This stage is related to the boundary type of the reservoir itself. When the boundary type of the reservoir is a constant pressure boundary, from the perspective of energy, the reservoir has sufficient external energy supply, and the pressure can be continuously conducted until the whole system is in quasi-steady state.

Sensitivity analysis

Based on the numerical solution for fracturing vertical well in a circular reservoir presented in the previous part, a sensitivity study for the parameters affecting the pressure and pressure derivative in the model is carried out. The intention of this study is to show the effect of each of these parameters on the dynamic behavior of fracturing vertical well in a circular reservoir. We evaluate the pressure transient solution by varying the values of six parameters including the fracture orientation, fracture half-length, elastic reservoir capacity ratio, exchange coefficient, skin factor and permeability ratio. The other parameters required for sensitivity analysis are shown in Table 1.

Fracture orientation

Fractures formed by hydraulic fracturing are random. Fracture orientation can be simply divided into two categories, that is, the fracture distribution is symmetrical about the wellbore (Fig. 7a) or not symmetrical about the wellbore (Fig. 7b). Figure 8 shows the fracture orientation mainly affects fracture linear flow. When the fracture distribution is symmetrical about the wellbore, the fluid in the reservoir can flow faster and more quickly to the wellbore, and the fracture acts as a highway connecting the reservoir and the wellbore rather than expanding the drainage area, on par with the other fracture orientation type.

Fig. 7
figure 7

The schematic diagram of fracture orientation

Full size image
Fig. 8
figure 8

The effect of fracture orientation on pressure curves

Full size image

Fracture half-length

As the scale of hydraulic fracturing is different, the fracture half-length formed in the reservoir is also different. The effect of the fracture half-length on pressure is shown in Fig. 9. Figure 9 shows that the fracture half-length mainly affects the stage A and B. As the fracture half-length decreases, the pressure propagation slows down, and the bottom hole pressure decreases. During the stage A, as the fracture half-length increases, the time of the stage A increases relatively, that is, the larger the fracture half-length is, the larger the seepage cross-sectional area of the fluid is, and the larger the liquid supply amount to the wellbore is, and the longer the stage A lasts under constant production condition. In addition, the fracture half-length only changes the amount of liquid supply, and it does not affect the speed of the liquid supply. Therefore, the pressure curves appear to be nearly parallel in stage A and B. The slope of the pressure curves is 1.

Fig. 9
figure 9

The effect of fracture half-length on pressure curves

Full size image

Elastic storage ratio

The essence of the elastic storage ratio is the ratio of the fluid volume in the matrix to the fracture. That is, the smaller the elastic storage ratio is, the smaller the percentage of oil and gas equivalent in the matrix is. The effect of the elastic storage ratio on pressure curves is shown in Fig. 10. Figure 10 shows that the elastic storage capacity ratio mainly affects the stage C, D and E, showing the width and depth of the “concave” curve. The larger the elastic storage ratio is, the less obvious the “concave” of the pressure curves is. When the elastic storage ratio is 0.05, the “step” segment in the pressure curves is almost invisible, which indicates almost no crossflow. The pressure curves approximate the characteristics of a single medium. It is mainly because when the elastic storage ratio tends to 1, the crossflow is not obvious, and the fluid flows to the wellbore through fracture.

Fig. 10
figure 10

The effect of elastic storage ratio on pressure curves

Full size image

Exchange coefficient

The exchange coefficient indicates the strength of fluid seepage between the matrix and the fracture. The larger the exchange coefficient is, the more easily the fluid flow from the matrix to the fracture. The effect of the exchange coefficient on pressure curves is shown in Fig. 11. Figure 11 shows that the exchange coefficient mainly affects the appearance time in stage E. The larger the exchange coefficient is, the earlier the "concave" section of pressure curves appears. Due to the wellbore storage effect, the exchange coefficient has no effect on pressure curves. With oil well producing, the fracture and matrix begin to supply fluid to the wellbore. The larger the exchange coefficient is, the fluid flows from the matrix to the fracture becomes much easier, and the crossflow occurs earlier. When the pressure of the fracture equals to the pressure of the matrix, the crossflow reaches a quasi-steady state, and there is no fluid exchanging between the matrix and fracture. The whole system is in a quasi-steady state. The pressure curves appear to coincide with each other in the later stages.

Fig. 11
figure 11

The effect of exchange coefficient on pressure curves

Full size image

Skin factor

The skin factor indicates the degree of pollution or modification near the wellbore. When it is more than zero, it indicates the reservoir near the wellbore has been damaged. On the contrary, the reservoir near the wellbore has been improved. The effect of the skin factor on pressure curves is shown in Fig. 12. Figure 12 shows that the skin factor mainly affects the stage C. The larger the skin factor is, the higher the “hump” peak of pressure derivative curve is. It is mainly because that as the skin factor increases, the pollution of the reservoir near the wellbore becomes more serious, and the additional pressure difference is greater. Only under the condition that the bottom hole pressure must be much bigger enough, can the fluid overcome the resistance of the additional pressure difference and successfully flow to the wellbore. However, the skin factor does not affect the speed of the radial flow, indicating that the pressure curves appear parallel to each other.

Fig. 12
figure 12

The effect of skin factor on pressure curves

Full size image

Permeability ratio

The permeability ratio of fracture to matrix is generally different, and it can be up to 10,000. In this paper, the permeability of the fracture is set to be constant, and only the permeability of the matrix is changed. The effect of permeability ratio on pressure curves is shown in Fig. 13. Figure 13 shows that with the permeability ratio decreasing, the peak of the "hump" of the pressure derivative curve becomes smaller. It is mainly because that the permeability of the matrix increases, the fluidity of the fluid in the reservoir becomes stronger, and the reservoir fluid can flow under a smaller displacement pressure difference. Therefore, on the pressure curve, the bottom hole pressure gradually decreases as the permeability ratio increases. It should be noted that when the permeability ratio is 1, there is no difference in fluidity between fracture and matrix, and the crossflow disappears.

Fig. 13
figure 13

The effect of permeability ratio on pressure curves

Full size image

Conclusion

A mathematical model of instantaneous pressure for unsteady flow was established here by considering the crossflow between the fractures and matrix. Different conditions, including the constant pressure condition, were considered. The basis for obtaining bottom hole pressure is to solve diffusivity equation with the integration of axisymmetric transformation and similar methods, which is presented for the first time. Different from the traditional method of using the Green’s function and source solution, this paper uses Laplace transformation, axisymmetric transformation and similar methods, separation of variables to obtain the analytical solution of Laplace domain. Then, the Stephenson Numerical method was used to obtain the numerical solution in a real domain. The results of this method agree with the numerical simulations and actual test data, suggesting this method is scientific and available. We also found that the pressure curves can be divided into eight stages, namely, early linear flow, continuous flow transition section, fracture linear flow, formation linear flow, crossflow, transitional flow, pseudo-radial flow and boundary control flow. The fracture orientation and skin factor mainly affect fracture linear flow. The fracture half-length mainly affects the early linear flow. The elastic storage capacity, exchange coefficient and permeability ratio mainly affect the crossflow. The validity and efficiency of this method suggest that it has potential to be used in practical tight oil exploitation.