Introduction

Understanding the phenomenon of transportation in porous media is the challenge of field development (Valvatne and Blunt 2004). Early studies of the two-phase flow continue from the early nineteenth century. In 1805, Young and other researchers improved surface tension theory (Blunt 2001). Craig conducted detailed studies on water flooding and oil displacement (Craig 1971). Hadia et al. (2007) and then Santosh et al. (2008) performed a lot of experimental tests and numerical solutions on a laboratory scale to analyze that which mechanisms affect water displacement. Using numerical simulations is useful for confirming some experimental observations and does not have the technical limitations of laboratories. In recent years, various types of fluid flow simulation methods have been proposed in porous media: pore network modeling (PNM), lattice Boltzmann method (LBM), volume of fluid (VOF) method, front tracking method (FTM), level-set method (LSM) and phase-field method (PFM) (Blunt 2001; Succi 2001; Hirt and Nichols 1981; Unverdi and Tryggvason 1992; Smereka and Sethian 2003; Badalassi et al. 2003). Using interface capturing methods (LSM, PFM) has become very popular because of the accuracy of computations in complex pore geometries and topological changes without the use of approximation in the using model (Yue et al. 2004; Sussman et al. 1999). It is very helpful to use pore-scale modeling (PSM) to understand two-phase phenomena. PSM can be used for a wide range such as capillary pressure and relative permeability and macro-scale flow simulation (Valvatne and Blunt 2004; Ramstad et al. 2009). The pore-scale simulation was performed by Ramstad et al. and Hatiboglu in 2D and 3D heterogeneous porous media with surface tension effect (Ramstad et al. 2009; Hatiboglu and Babadagli 2007). The first idea for PFM was presented in 1979 when van der Waals used his model for a system of liquid–gas by the mean of a density function that its changing interface was constant. The convective Cahn–Hilliard equation (1958) was implemented in 1999 by Jacqmin in 2D and 3D (Jacqmin 1999). The approach used by PFM is the physical relationship between the phases that the system's free energy contains. In other words, PFM includes both current and ensures that the overall energy of the system is kept to a minimum. (Zhou et al. 2010). PFM computes 2-phase flow on a fixed Eulerian grid, the entire domain state is represented by an indicator function supposing different constant values for every phase. Also, there are variations in the interfacial region, and these values, in reality, undergo rapid but smooth (Smereka and Sethian 2003). The pros and cons of PFM have been investigated more by some researchers (Smereka and Sethian 2003; Feng et al. 2005). In recent years, a variety of software has been developed to solve the PFM Cahn–Hilliard equation to simulate the two-phase Navier–Stokes flows (Liu and Shen 2003; Chiu and Lin 2011; Bogdanov et al. 2010). In some studies, some researchers looked at the Influence of contact angle on flow patterns and fluid saturation (Martys et al. 1991; Akhlaghi Amiri and Hamouda 2014). Surfactants are usually organic compounds that have hydrophobic and hydrophilic groups. Therefore, they are usually soluble in water and organic solvents. These fluids greatly reduce interfacial tension between fluids when they spread on the surface of a liquid (Kathel and Mohanty 2013). Also, interfacial tension forces affect the level between solid and liquid and cause a change in the wettability of the solid surface of the porous media (Rostami 2019). The importance of using surfactants in chemical flooding has been extensively studied, which can be described as influencing factors in the success of this flooding as follows: temperature, optimal salinity, branched surfactants, zeta potential, pH, and pressure (very low) (Chegenizadeh and Saeedi 2017; Hara et al. 1999). On the other hand, determining the concentration range for industrial and economic purposes is very effective in chemical injection. Because the surfactants in the injection must retain their properties and be economically viable. The concentration of a surfactant as a solvent in the solvent phase reaches such a level that the surfactant molecules aggregate (micelle formation) is called CMC. It is at this time that adsorption occurs and interfacial tension (IFT) or surface tension (SFT) reach their minimum amounts (Schramm 2000). Therefore, before using real micromodels, a model was created a need to use simulation to study the predictions and behaviors that a model was created may encounter from flooding in a real micromodel. In this study, the analysis of oil displacement by water and surfactant at the pore scale is presented by using existing Finite Element Methods in COMSOL Multiphysics 5.3a and its purpose is to compare oil produced from synthetic micromodel. To create a physical model that can be accessed by COMSOL software, a model was created the need to process the image with the MATLAB software and then Rhino to convert the original image into an accessible file. The original image is of a porous media of Kansas sandstone (http://www.kgs.ku.edu/Publications/Oil/primer03.html).

Simulation and comparison of a two-phase experimental model

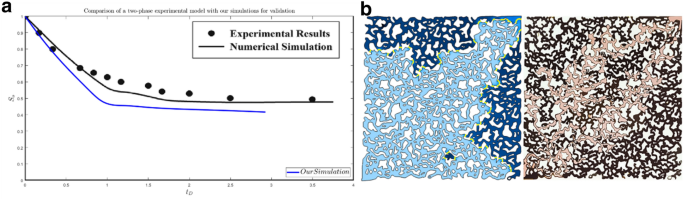
Maaref et al. investigated two-phase flow and the effect of wettability, heterogeneity, and viscosity in experimental and simulated porous media. In one part of their study, they considered a basis model (Case 1) and compared experimental and simulation results for waterflooding. (Maaref et al. 2017). To recover their study, the rock and fluids properties and solution conditions are in Tables 1, 2 and 3.

Table 1 Summary of rock properties used in two-phase comparison
Full size table
Table 2 Summary of fluid properties used in two-phase comparison
Full size table
Table 3 Summary of solution conditions used in two-phase comparison
Full size table

The results obtained from this simulation are plotted as a mask on the results of their study in Fig. 1a, and the situation of phases at the breakthrough time (tD = 1) is shown in Fig. 1b.

Fig. 1
figure 1

a. Comparison of simulation and experimental results, b. Comparison of graphic results at breakthrough time

Full size image

This investigation showed that the simulation shows a deviation which can be due to selecting the unsuitable threshold for a binary image, removing some edge details to reduce the lines and smooth them, or choosing coarse mesh to speed up the solution.

BSE images

Of the finite element simulation requirements is the pore geometry of the image sample, which, as will be explained in this section, is obtained in two steps. First, a BSE image is selected for the sample, and then, using a scale conversion, the BSE image is used as a physical geometry for the numerical solution output. Image processing methods are used to connect these two stages (Gunde et al. 2010).

Image processing in order to build a physical model

At this stage, image processing is performed on a sand section. In this study, after performing image thresholding, image morphology operators such as erosion operator, removal of small objects, and then expansion are used which will improve binary image (Gonzalez and Woods 2002). After making changes to the binary image, the intensity of the changes was not sufficient, so with the help of rhino software a model was created to smooth the edges of the image. The porous media created in CAD format (.dxf) is ready to be imported into COMSOL software, (Fig. 2).

Fig. 2
figure 2

a BSE image of sample sandstone. b Manual thresholding for binary construction. c Otsu thresholding. d Binary image by performing morphological operators. e Improved image in Rhino software. f File (.dxf) format imported into COMSOL software

Full size image

Numerical simulation

The equations governing two-phase flow in physical geometry that are solved directly are presented in this section.

Geometry and fluids of porous media

After importing the porous media file into COMSOL software, the porosity and dimensions can be measured. The porosity and dimensions of the micromodel are shown in Table 4.

Table 4 Properties of porous media
Full size table

The water's generally known properties can be seen in Table 5. The properties of SDS should also be calculated according to the concentration and a function for it should be determined in different concentrations. Kushner et al. (1952) studies showed that the density and viscosity of water-soluble SDS anionic surfactant varied at different concentrations (Kushner et al. 1952). Qi et al. (2014) also illustrated that IFT and contact angle depend on surfactant concentration and oil composition (Qi et al. 2014). Although there is a different range from the CMC point of this surfactant at different temperatures, we know that at 25 °C the CMC is about 8.2 mM (2365 ppm) (Tadros 2005; Mukerjee and Mysels 1972). In this study, a model was developed to inject fluid into the model at the inlet boundary with a concentration of 1000 ppm (3.4677 mol/m3), because the concentration in the elements does not change suddenly and increases over time. The general properties of the oil, water, and SDS are presented in Table 5. The SDS properties are presented as a function of concentration through Eqs. 1 to 4.

$$\rho_{{{\text{SDS}}\left( c \right)}} = 0.049c + 997.56$$
(1)
$$\mu_{{{\text{SDS}}\left( c \right)}} = 9.378 \times 10^{ - 4} + 2.88372 \times 10^{ - 7} c$$
(2)
$$\sigma_{{{\text{SDS}}\left( c \right)}} = \frac{{0.06035c^{2} - 0.2031c + 0.2247}}{{c^{3} + 104.9c^{2} - 28.98c + 65.91}}$$
(3)
$$\theta_{{{\text{SDS}}\left( c \right)}} = 4.364 \times 10^{15} e^{{ - \left( {\frac{c + 43.55}{{7.269}}} \right)^{2} }} + 7.46 e^{{ - \left( {\frac{c - 39.15}{{20.91}}} \right)^{2} }}$$
(4)
Table 5 Properties of fluids
Full size table

Governing equations

The fluid flow and Interfacial tension equations are presented in this section to provide a mathematical model governing the porous media.

Fluid flow equation

The fluid flow equation to continuity for incompressible fluid is as follows (Panton 2004),

$$\rho \left( {\frac{{\partial {\mathbf{v}}}}{\partial t} + \left( {{\mathbf{v}}.\nabla } \right){\mathbf{v}}} \right) = - \nabla {\mathbf{p}} + \rho {\mathbf{g}} + \mu \left( {\nabla {\mathbf{v}} + \nabla^{T} {\mathbf{v}}} \right) + {\mathbf{F}}_{{{\mathbf{st}}}}$$
(5)

Newtonian and incompressible fluids are assumed: dynamic fluid viscosity (μ), fluid density (ρ), fluids apparent velocity (v), fluid pressure (p), gravitational acceleration (g), and interfacial tension force term (Fst).

Interfacial tension and phase field method

Two approaches of LSM and PFM can be used to calculate and display the interfacial tension force. In this paper, the PFM method is used (Akhlaghi Amiri and Hamouda 2013). Assuming that the convection equation of Cahn–Hillard is a time-independent form of the energy minimization concept, then:

$$\frac{{\partial \phi_{{{\text{PF}}}} }}{\partial t} + {\mathbf{v}}.\nabla \phi_{{{\text{PF}}}} = \nabla .\left( {M\nabla G} \right)$$
(6)

Here G is the chemical potential of the system and M is the diffusion coefficient called mobility. Mobility can be expressed as:

$$M = M_{c} \varepsilon_{{{\text{PF}}}}^{2}$$
(7)

Here Mc is the characteristic mobility and εPF is a capillary width scaled according to PFM interface thickness. The chemical potential is calculated from:

$$G = \lambda \left[ {1/\varepsilon_{{{\text{PF}}}}^{2} \phi_{{{\text{PF}}}} \left( {\phi_{{{\text{PF}}}} - \frac{1}{2}} \right)\left( {\phi_{{{\text{PF}}}} - 1} \right) - \nabla^{2} \phi_{{{\text{PF}}}} } \right]$$
(8)

where λ is the mixing energy density. So, by coupling Eqs. 5, 6 a model was created get an immiscible two-phase flow problem:

$$\rho_{\left( \phi \right)} \frac{{\partial {\mathbf{v}}}}{{\partial {\text{t}}}} + \rho_{\left( \phi \right)} {\mathbf{v}}.\nabla {\mathbf{v}} = - \nabla {\mathbf{p}} + \rho_{\left( \phi \right)} {\mathbf{g}} + \left[ {\mu_{\left( \phi \right)} \left( {\nabla {\mathbf{v}} + \nabla^{{\text{T}}} {\mathbf{v}}} \right)} \right] + {\mathbf{F}}_{{{\mathbf{st}},{\mathbf{PF}}}}$$
(9)

where Fst, PF is:

$${\mathbf{F}}_{{{\mathbf{st}},{\mathbf{PF}}}} = {\text{G}}\nabla \phi_{{{\text{PF}}}}$$
(10)

Initial and Boundary conditions

Initial and Boundary conditions used for the equations are discussed here. In the beginning, the initial fluid in the porous media is oil, and gradually the injected fluids enter from the left (Fig. 3a). The oil is transported in porous media and exits through the right boundaries. In this study, the flow is considered horizontally and a model was created does not have gravitational forces. The walls are initially oil-wet and gradually will lose this property in contact with the surfactant SDS aqueous solution. Achieving a stable numerical simulation with wetted wall conditions is determined. These values are presented in Table 5 and Eq. 4. The inlet boundary condition for the pressure is 30 psi and the outlet boundary condition initial fluid pressure in the porous media is 14.69 psi. By these boundary conditions, the laminar flow is established and the Reynolds number remains below 1. The water saturation boundary condition for injection is 1 and the initial value in the porous media is 0, also Vf is injection volume fraction which is gradually distributed in porous media.

Fig. 3
figure 3

a. Input and output display in sample micromodel, b. The micromodel image imported into the software and the two-dimensional mesh generated in the geometry

Full size image

For water injection, the applied conditions are:

$$- P_{0} n_{{{\text{inlet}}}} = 30 \left[ {{\text{psi}}} \right]$$
(11)
$$\phi_{{{\text{PF}},{\text{inlet}}}} = 2V_{{\text{f}}} - 1,V_{{\text{f}}} = 1 \to \phi_{{{\text{PF}},{\text{inlet}}}} = 1$$
(12)
$$- P_{0} { }n_{{{\text{outlet}}}} = 14.69{ }\left[ {{\text{psi}}} \right]$$
(13)
$$\phi_{{{\text{PF}},{\text{outlet}}}} = 2V_{{\text{f}}} - 1$$
(14)
$$u_{{{\text{wall}}}} = 0$$
(15)
$$n_{{{\text{wall}}}} .\varepsilon_{{{\text{PF}}}}^{2} \nabla \phi_{{{\text{PF}}}} = \varepsilon_{{{\text{PF}}}}^{2} {\text{cos}}\left( {\theta_{i} } \right)\left| {\nabla \phi_{{{\text{PF}}}} } \right|{ },\left\{ {\begin{array}{*{20}c} {\frac{5}{\pi 6} , i = w} \\ {Eq.4 , i = {\text{SDS}}} \\ \end{array} } \right.$$
(16)
$$- P_{{0,{\text{initial}}}} = 14.7{ }\left[ {{\text{psi}}} \right]$$
(17)
$$\phi_{{{\text{PF}},{\text{initial}}}} = 2V_{{\text{f}}} - 1,V_{{\text{f}}} = 0 \to \phi_{{{\text{PF}},{\text{initial}}}} = - 1$$
(18)

And for the surfactant injection, the above equations are considered with these conditions:

$$c_{{0,{\text{inle}}t}} = 3.4677{ }\left[ {{\text{mol}}/m^{3} } \right]$$
(19)
$$c_{{{\text{outlet}}}} = - n_{{{\text{outlet}}}} D_{{{\text{sds}}}} \nabla c = 0$$
(20)
$$- n_{{{\text{wall}}}} N = 0{ },{ }N {\text{is source term}}$$
(21)
$$- c_{{0,{\text{initial}}}} = 0{ }\left[ {{\text{mol}}/m^{3} } \right]$$
(22)

Solution technique

To perform and advancing in simulations a software based on the finite element method (COMSOL Multiphysics (5.3a) by COMSOL Inc.) is used. The computed physical model is divided into several elements consisting of a 2-dimensional mesh, as depicted in Fig. 3b. The mesh contains 312,493 elements (coarse mesh). The FEM solver uses the MUMPS (Multifrontal Massively Parallel Sparse Direct Solver) linear system solver to calculate the values of pressure, velocity, and phase-field function for the nodes around each element. It then calculates these values using the shape function for each element. To select the tolerance threshold, the relative tolerance of 0.01 was selected. The time-stepping method uses the generalized alpha method to estimate each time step. SDS and Waterflooding start at 0 ms and the simulation would run for 4.5 ms. According to the complex meshing in the physical model and the conditions placed at the boundaries; The simulator took about 2–6 h to solve the convergent problem. Therefore, due to the computational constraints of the problem, both fluid displacement simulations were performed for 4.5 ms.

Results and discussion

Two-phase fluid flow in a porous media is an important type of fluid flow that occurs during production from a hydrocarbon reservoir, injecting fluid into a reservoir during extraction processes, or storing hydrocarbons in an existing reservoir. In this section, a model was created wants to investigate and compare the behavior of water injection fluid flow and SDS surfactant with a final concentration of 1000 ppm. First, a model was created to calculate the volume of oil in the micromodel using COMSOL, which is 1.055 mm2. Then, at each time step, by applying the average volume fluid fraction operator on the surface of the porous media, the percentage of oil saturation is obtained at any time. By multiplying the oil saturation by the initial volume, the amount of residual oil volume is calculated, which can simply be used to calculate the volume of oil produced at any given time. Another purpose is to visualize the displacement of injected fluid and how the oil is trapped in the pores.

Water flooding

Figure 4 shows how water flows against oil in a porous media for 16 selected times, in the range of 4.5 ms. Also, in this figure, a model was created to see the fluid flow in the time steps 0.75–4.5 ms. The black area is oil and the blue area is the injection fluid (water). The green line contour represents the 10% saturation and the yellow line contour represents the 90% saturation with injected fluid (water). The velocity vector, which contains the direction of the fluid flow, is visible with red arrows.

Fig. 4
figure 4

16-time steps for 4.5 ms, black areas indicate oil and blue areas represents water, green contours are for 10% saturation and yellow contours are for 90% saturation of water

Full size image

Surfactant flooding

When a model was created want to inject fluids that create new rheological properties by changing the concentration, a model has created the need to define two mass diffusivity coefficients (Dc) for injecting fluid into oil and oil into injecting fluid. These values are heavily dependent on the composition of the oil, the concentration of surfactant, and the diameter of the channels (roughly in nanoscale) that this mass transfer takes place in. However, in this section, the diameter of the channels is not in nanoscale and a model was created to assume that the oil does not diffuse into the oil and the diffusion coefficient water-soluble surfactant is a constant number with a value of 4.58 × 10–11 m2/s (Jarvet et al. 2007). In Fig. 5, a model was created that can see the fluid flow in the time steps 0.75–4.5 ms. The black area is oil and the blue area is the injection fluid (SDS). The green line contour represents the 10% saturation and the yellow line contour represents the 90% saturation with injected fluid (SDS). The velocity vector, which contains the direction of the fluid flow, is visible with red arrows. Figure 6 shows the recovery factor by percentage at all simulation times for water (blue) and surfactant (green).

Fig. 5
figure 5

16-time steps for 4.5 ms, black areas indicate oil and blue areas represents surfactant, green contours are for 10% saturation and yellow contours are for 90% saturation of surfactant

Full size image
Fig. 6
figure 6

Recovery factor vs. time, water (blue) and SDS surfactant (green)

Full size image

As it was mentioned before, the porous media is naturally oil-wet before simulation began. As it can be seen in Fig. 7 a, c water injection did not change the wettability of the porous media walls. Instead, injection of surfactant has caused wettability alteration (Fig. 7b, d). Figure 7 also shows a comparison of the two channels in the amount of trapped oil.

Fig. 7
figure 7

The comparison of residual oil in two different channels with water and surfactant injection. a. The first channel by water injection, b. The first channel by SDS injection, c. the Second channel by water injection, d. The second channel by SDS injection

Full size image

The phenomenon a model was created may encounter during simulation is a sudden and rapid change of wettability on the walls. This phenomenon occurs in wide channels and causes the oil to form droplet in them and the injected fluid continues its way out by bypassing it. As it can be seen in Fig. 8. a., water injection does not keep the droplets in place. But Fig. 8b shows the oil droplet in the same porous media.

Fig. 8
figure 8

a. The place where oil has not created oil droplets with water flooding. b. The place where oil has created oil droplets with surfactant flooding

Full size image

If in surfactant injection, a model was created showing the frontal advance 50% saturation (0.5 volume fraction) with blue color and the frontal advance 50% concentration (500 ppm) with red color, it can be seen that the saturation front causes fluid to flow in wide channels and the concentration front in narrow channels. As shown in Fig. 9a, both fronts are flowing at the same speed at the start of the injection. Over time and with the progression of the fluid in wide channels, the saturation front exceeds the concentration front (Fig. 9b) and finds its path (Fig. 9c). The concentration front when reaches a position where it should select a path (Fig. 9d). The concentration front by advancing into the narrow channels, causes the fluid to flow in this narrow channel and also opens the way for the saturation front (Fig. 9e) and finally overtakes the saturation front (Fig. 9f).

Fig. 9
figure 9

The situation and following 50% saturation and concentration fronts in channels with different widths throughout the porous media

Full size image

Conclusion

Simulation of water and surfactant injection into a porous media containing oil was performed using the computational fluid dynamics method on the image of a real micromodel. Although at the first view, the model showed high recovery from surfactant flooding, after converting the average residual oil to the produced oil and converting the produced oil to recovery factor, it was observed that the recovery factor obtained by water injection is 55.49% and the same value for surfactant injection is 57.70%. Therefore, using the surfactant leads to an increase of 2.21% in the model recovery factor after 4.5 ms. It can also be concluded that the injection of surfactant by itself does not have a significant effect on increasing efficiency and should be accompanied by fluid before or after injection. On the other hand, trapping oil in wide canals is a challenge that comes with surfactant injection and more studies should be done in this field.