Introduction

In hydrocarbon exploration and production, the prediction of rock and fluid properties has remained the ultimate goal of seismic inversion and reservoir characterization employed in delineating hydrocarbon saturated reservoirs (Akpan et al. 2020). A significant aspect employed in the interpretation of seismic data involves carrying out detailed investigation of seismic properties, which produces information relating to hydrocarbon fluids (oil, gas and water). One method of achieving this objective is through the conversion of the observed seismic response using an inversion process into velocity and impedances (acoustic, shear and elastic). These parameters (velocity and impedance) are the fundamental physical properties of a rock, which is employed to infer fluid and lithology in the exploration of oil/gas prospects. The application of seismic technique has led to the development of several seismic inversions in the industry today. Based on the type of seismic data employed in analysis, seismic inversion is grouped into two major categories—poststack and pre-stack method of inversion. Poststack seismic inversion method relies on model building using well log, seismic and geological data (Simm and Bacon 2014; Veeken and Da-Silva 2004; Downtown 2005). The pre-stack seismic inversion method is the most commonly used method of inversion, which enables the removal of wavelet effect from the seismic data and produces a high resolution image of the subsurface (Margrave et al. 1998; Veeken 2007; Moosavi and Mokhtari 2016). Okeugo et al. (2018) opined that, the major advantage of utilizing the pre-stack seismic inversion in the construction of reliable earth model and lithofacies characterization is because of the ability of the technique to extract more information such as shear velocity from the sampled seismic data. The extracted shear wave velocity information helps in giving a better discrimination of the reservoir and non-reservoir rocks, which are not achieved through the poststack seismic inversion method.

Over the years, the use of acoustic impedance (IP) and shear impedance (IS), which are products of seismic inversion in discriminating fluid and lithologies have posed challenges and difficulties to reservoir characterization. These challenges are attributed to the overlap observed in the inverted IP and IS attribute values as their values are not unique to clearly discriminate lithologies and fluid (oil, gas and brine). Poisson’s impedance developed by Quackenbush et al. (2006) addresses this challenge because the attribute (PI) incorporates information from Poisson’s ratio and density into a single attribute. Nanda (2016) defined Poisson’s ratio as an elastic constant, which characterizes a porous reservoir rock with its fluid content. Poisson’s impedance emerged as a result of the pitfall observed from other methods of seismic inversion employed in characterizing hydrocarbon reservoirs. The ability to differentiate fluids and lithology in the reservoir through Poisson’s impedance inversion has over the years produced remarkably achievement in the oil/gas industry. Accessible literature from different hydrocarbon producing basins across the globe reveals that PI attribute has been successfully applied in delineating hydrocarbon and brine saturated sands from shales (Haris et al. 2017; Zhou and Hilterman 2010; Presteyo et al. 2017; Omudu et al. 2007; Zhou and Hilterman 2010; Tian et al. 2010). It is thus, from the enormous achievement of the PI technique in the oil/gas sector that this study aims to employ PI in delineating hydrocarbon saturated reservoir and estimating the areal spread of the reservoir in Bonna field. This will contribute to the increase in the production of the world’s most demand energy source (hydrocarbon) and boost the economy of Nigeria, which relies solely on oil exportation.

Location and geology of the study area

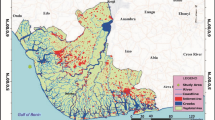
Bonna field is one of the hydrocarbon exploration fields situated in the coastal swamp depobelt of the prolific Niger Delta Basin (Fig. 1a). The base map of the study area (Fig. 1b) shows location of the wells and seismic line connecting three wells: Bonna-9, Bonna-6 and Bonna-8 in the field. The Niger Delta Basin is situated in the Southern part of Nigeria bordering the Atlantic Ocean between latitudes 30 N and 60 N and longitudes 40E and 80E (Ejedawe et al. 2007). Weber and Daukoru (1975) attributed the formation of the basin to the build-up of sediments associated with rift faulting during the Precambrain. Several exploration activities have been ongoing in the Niger Delta Basin since the discovery of commercial hydrocarbon in 1956. Alao et el. (2013) classified this sedimentary basin as one of the hydrocarbon productive basins in the world. Presently, the basin is Nigeria’s most explored sedimentary basin, which serves as a major source of income to the nation. The areal coverage of the Niger Delta Basin is estimated to be about 75,000 square kilometres. In the Eastern Nigeria, the basin extends from the Calabar Flank and the Abakaliki trough to the Benin flank in west and opens to the Atlantic Ocean in the south (kulke 1990; Doust and Omatsola 1990; Nwankwo et al. 2014). The overall sediment volume in the Niger Delta is estimated to be approximately 500,000 km3 with sedimentary thickness of about 10 km around the depocenters (Hospers 1965; Kaplan et al. 1994). According to Wu and Bally (2000), the Niger Delta Basin is regarded as a classical shale tectonic province due to the presence of overpressured shales and shale diapric structures associated with the area. One petroleum system has been identified in the Niger Delta Province which is referred to as the Tertiary Niger Delta (Akata–Agbada) petroleum system.

Fig. 1
figure 1

(a) Niger Delta depobelt map showing the location of Bonna field (Ejedawe et al. 2007) (b) Base map of Bonna field showing seismic Inline/Xline and locations of the wells

Full size image

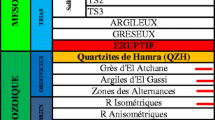
The Tertiary Niger Delta is divided into three major subsurface lithostratigraphic units—the Akata, Agbada and Benin Formations as shown in Fig. 2. The lithologies of these Formations comprise of sands, silts and shales alternations, which are arranged within 10–100 ft successions, and defined by progressive upward changes in grain size and bed thickness (Okeugo et al. 2018). The Akata Formation is deep marine shales with age ranging from Eocene to recent and serves as a source rock for hydrocarbon in the basin (Reijers 2011; Lawrence et al. 2002; Short and Stauble 1967). This formation is the oldest of the three formations in the Niger Delta Basin with thickness estimated to be about 7000 m (Doust and Omatsola 1990). The Agbada Formation overlies the Akata Formation and consists of sandstone–shale alternations with thickness of about 3700 m. The Agbada Formation forms the main reservoir and seal for hydrocarbon accumulation in the basin. Hydrocarbon in the Niger Delta is produced from the sandstones and consolidated sands predominantly in the Agbada Formation. The Benin Formation is the youngest and overlies the Agbada Formation with thickness described by Whiteman (1982) to be about 280 m and up to 2100 m in region with maximum subsidence. This Formation make up the top part of the Niger Delta clastic wedge, which forms the Benin–Onitsha area in the north and it is beyond the coastline (Short and Stauble 1967).

Fig. 2
figure 2

The Niger Delta lithostratigraphic succession showing the lithologic units of the formations (Lawrence et al. 2002)

Full size image

The conceptual framework

Poisson impedance is defined as the difference between the P-impedance (Ip) and a scaled version of the S-impedance (Is) where the term (c) is the scalar, which can be determined from the slope of the regression line between Ip and Is. Poisson’s impedance is represented mathematically as given in Eq. 1;

$${\text{PI}} = I_{P} - cI_{S}$$
(1)

where PI is the Poisson impedance, IP is the acoustic impedance, IS is the shear impedance and c is the rotation optimization.

The value of c is estimated from the regression line of the crossplot of IP versus IS logs for the wet trend. The c value is derived from the inverse of the slope of IP versus IS crossplot. Poisson impedance attribute is one of the rock physics parameters, which can be applied practically in the prediction of reservoir and detecting the presence of hydrocarbon (Presteyo et al. 2017). The Poisson’s impedance theory is illustrated by Quackenbush et al. (2006) as shown in the PI versus SI crossplot space shown in Fig. 3. This attribute incorporates both Poisson’s ratio and density information into a single attribute, which optimizes the discrimination of litho-fluid by choosing an axis of rotation in the PI versus SI crossplot (Fig. 3). The rotation is optimized by the constant term c as deciphered in Fig. 3, the data clouds are not discriminated along the PI or SI axes alone but with a rotation of the axis represented by the dotted line, the data clouds are perfectly discriminated.

Fig. 3
figure 3

Schematic representation of IP versus IS crossplot space showing oil sand, brine sand and shale sand distribution, (Quackenbush et al. 2006)

Full size image

Materials and method

The data set obtained for this study comprises a suites of well logs from seven exploratory wells and 3D pre-stack seismic volume in Bonna field. Although seven (7) wells are in the field, relevant well log data were available from two wells labelled Bonna-6 and Bonna-8 (Figs. 4 and 5). The log data include resistivity, caliper, density, gamma ray and P-wave. The well log data deciphered only a section of gamma ray and resistivity logs, which were used in delineating the reservoir sands from the well log labelled BN reservoir and the computed Poisson’s impedance (PI) curve superimposed with Poisson’s ratio curve signature as shown in track 3. The well log data were median filtered to correct for borehole irregularities using an operator length of six (6) which was observed to be suitable to preserve signals in the data. Shear wave velocity (S-wave) was estimated using Castagna and Greenberg (1993) relation given in Eq. 2 and Eq. 3 for sand and shale beds as there was no S-wave information for the two wells. The general workflow which illustrates the study methodology is shown in Fig. 6.

Fig. 4
figure 4

Bonna-6 well log showing gamma ray, resistivity, Poisson’s ratio and Poisson’s impedance

Full size image
Fig. 5
figure 5

Bonna-8 well log showing gamma ray, resistivity, Poisson’s impedance and Poisson’s ratio

Full size image
Fig. 6
figure 6

Summarized workflow illustrating the study methodology

Full size image
$$V_{S} = 0.80416V_{P} - 0.85588$$
(2)
$$V_{S} = 0.76969V_{P} - 0.86735$$
(3)

Acoustic impedance (AI) log, which is the product of compressional seismic wave velocity and formation bulk density was estimated for the two wells using Eq. 4. Shear wave velocity was substituted into Eq. 4 to obtain Eq. 5 which was employed in estimating shear impedance (SI) log required for the AI versus SI crossplot. The AI-SI crossplot space in which the value of ‘c’ term was estimated is shown in Figs. 7 and 8. The crossplot space shows clusters corresponding to the presence of different formation fluids inferred in the study area.

Fig. 7
figure 7

S-impedance versus P-impedance crossplot space colour coded with gamma ray log for Bonna-6

Full size image
Fig. 8
figure 8

S-impedance versus P-impedance crossplot space colour coded with gamma ray log for Bonna-8

Full size image
$$AI = \rho V_{P}$$
(4)
$$SI = \rho V_{S}$$
(5)

where ρ is the density and VP and VS are the seismic wave velocities for compressional and shear wave, respectively.

Simultaneous seismic inversion which relies on the background relationship between In(Zp), In(Zs) and In(Dn) was carried out using intervals around the well locations. The coefficients (k, kc, and mc) were estimated from the crossplot relation shown in Fig. 9. Deviations of these values from the background In(Zp), In(Zs) and In(Dn) were calculated from the inversion output. The calculated values were initialized to zero in the initial model, and the final inversion was determined by utilizing the estimated coefficients of (k, kc and mc). Again, from the crossplot of P-impedance versus S-impedances (Figs. 7 and 8), the wet trend regression was extrapolated.

Fig. 9
figure 9

Well log data clusters in coloured dots and the interpreted background relationships between In(Zp), In(Zs) and In(Dn) for the two wells

Full size image

The 3D seismic data were simultaneously inverted to obtain density, PI, Vp− Vs ratio, compressional and shear wave impedances. The inversion was initiated by first building an initial model using P-wave, S-wave and density logs around the well location. The initial model building involved the extraction of wavelet, which was extracted using the two wells and after the seismic to well-tie process, a final wavelet with updated low frequency was obtained as shown in Fig. 10c. The initial P-impedance model with the inserted P-impedance curve and the picked BN horizon which runs across the Bonna 3D seismic section is shown in Fig. 10a. The extracted wavelet with updated low frequency and the picked BN horizon were employed in the initial model building and subsequent inversion process. A low pass filter was applied to filter the model using a frequency of 10 Hz. This was done in accordance with (Hampson and Russell 2016) to remove the heterogeneity at the seismic frequencies arising from the well log data and preserve the low frequency component. The picked BN horizon structure, which was also employed in the inversion, is shown in Fig. 10b. The horizon structure reveals that the wells in Bonna field are located on a low seismic arrival time. This horizon structure map was used as a guide for interpolation between the wells employed in building the initial model. The seismic volume was inverted using an inversion time interval of 2000 ms to 2400 ms, 50 number iterations, while 1.40, −4.63, 0.39 and −3.25 were the constants chosen for the coefficients k, c, m, and mc, respectively.

Fig. 10
figure 10figure 10

(a) P-impedance model section showing two wells (b) event time structure (c) corrected wavelet phase and frequency response

Full size image

Results and discussion

The crossplot results of density versus Poisson’s ratio colour coded with Poisson’s impedance (PI) are shown in Figs. 11 and 12 for Bonna-6 and Bonna-8, respectively. The results depict clusters discriminating the fluid and lithology in the field. Three (3) distinct zones are mapped out which are circled in purple, red and black colours for Bonna-6. These zones are interpreted to correspond to gas sand unit, brine saturated sand and shale beds, respectively. In Bonna-8, the crossplot space deciphered clusters separated into two major zones which are circled in purple and black colours. The discrimination of fluid and lithology in this case reflect separation attributed to the presence of gas sand unit in green converging clusters and shale in clusters converging in cyan to purple colour which acts as a seal to the fluid saturated rock. These delineated lithologies are typical of the Niger Delta lithologic sequence where the study area is situated.

Fig. 11
figure 11

Crossplot of density (ρ) versus Poisson’s ratio colour coded with PI for Bonna-6

Full size image
Fig. 12
figure 12

Crossplot of density (ρ) versus Poisson’s ratio colour coded with PI for Bonna-8

Full size image

The cross section of the inverted PI from time window of 2000 ms to 2400 ms, is shown in Fig. 13. The result reveals a potential prospect beneath BN horizon at a time of 2234 ms which, cut across the section. It shows two inserted well logs of gamma ray (black curve) labelled Bonna-6 and Bonna-8, which were connected using the seismic line in the base map (Fig. 1b). Separation in colours are also deciphered in the section, which corresponds to the various lithologies in the study area. These colours (green, red, blue, cyan and purple) indicate the presence of sand, sand-shale and shale beds. The low PI in green to yellow with PI values ranging from \(5.0 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) to \(5.2 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) corresponds to sand lithology. The intermediate PI values in red to cyan colours are the sand-shale region with PI values ranging from \(5.2 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) to \(5.4 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). Shale beds are characterized with highest PI values ranging from \(5.4 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) to \(5.6 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) deciphered in blue to purple colours. The result further reveals the lateral spread of the low PI sand zones inferred to be potential prospect as deciphered in the section.

Fig. 13
figure 13

Inverted cross section of PI

Full size image

The pre-stack simultaneous inversion results obtained for P-impedance, S-impedance, density, VP− VS ratio and Poisson’s impedance are shown in Figs. 14, 15, 16, 17, 18, respectively. These attribute slices were generated using the picked BN horizon level averaged within a time window of 10 ms. The various results depict the strength of each attribute in delineating the probable reservoir zone in the study area. The P-impedance (Zp) amplitude slice shown in Fig. 14 depicts low impedance around the well locations. But, the delineated zones from this P-impedance attribute do not clearly separate the probable reservoir edges. The areas surrounding Bonna-9 and Bonna-10 depict low impedance in green to yellow colour with values ranging from \(1.8 \times 10^{4} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) to \(2.1 \times 10^{4} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). S-impedance attribute, which is a derived seismic attribute obtained from the product of shear wave velocity (VS) and density (ρ) is shown in Fig. 15. The S-impedance attribute reveals the probable reservoir sands around the well locations. The figure depicts a much lower impedance values when compared with the acoustic impedance cross section of Fig. 14. The S-impedance values around the well locations range from \(9.2 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\) to \(1.1 \times 10^{4} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). This zone with green–yellow colour corresponds to the hydrocarbon saturated sand reservoir deciphered in the acoustic impedance cross section of Fig. 14. The areas away from the suspected hydrocarbon saturated zone represent the shale-sand region in red colour code. Further, inspection of this attribute reveals that the inverted S-impedance amplitude slice has three major separations ranging from green, yellow and red colour codes.

Fig. 14
figure 14

Cross section of P-impedance amplitude attribute slice

Full size image
Fig. 15
figure 15

Cross section of S-impedance amplitude attribute slice

Full size image
Fig. 16
figure 16

Cross section of VP− VS ratio amplitude attribute slice

Full size image
Fig. 17
figure 17

Cross section of density amplitude attribute slice

Full size image
Fig. 18
figure 18

Cross section of Poisson’s impedance amplitude attribute slice

Full size image

The VP− VS ratio is the ratio of the compressional wave velocity (VP) to the shear wave velocity (VS). Dagogo et al. (2016) pointed out that this seismic attribute can be very diagnostic of fluid saturation because fluids do not shear and hence do not support shear wave transmission. The inverted amplitude slice of VP− VS ratio obtained in Bonna field is shown in Fig. 16. This result reveals zones surrounding the well locations as reservoir sand saturated with probable hydrocarbon fluid. The well locations depict low VP− VS ratio ranging from 1.65 to 1.72. The low VP− VS ratio values are observed around the well locations of Bonna-6, Bonna-7 and Bonna-8 with much lower value deciphered around Bonna-7. This is viewed to be indication of the presence of gas. These values are within the values which indicate the presence of hydrocarbon when compared with the standard variation in VP− VS ratio given by Veeken (2007) for hydrocarbon saturation in oil/gas field.

The bulk density of a formation gives a measure of formation density which includes the density of the fluid and the rock matrix. The bulk density attribute slice in Bonna field, which was also cut for comparison, is shown in Fig. 17. The result equally portrays the delineated zone as area with low density typical of a hydrocarbon accumulated zone, when compared to the surrounding rock. The density values ranged from 1.96 to 2.14 g/cc within the well locations indicating a high chance of accumulation with an appreciable volume of hydrocarbon. This range of density is in accordance with the standard density values for a reservoir capable of accommodating hydrocarbon fluids. Density estimation is very important in reservoir delineation activities because low density values are associated with many high quality reservoirs as gas and oil saturated rocks are characterized with low densities compared to brine saturated rocks (Quackenbush et al. 2006). The lowest density value is observed around the well locations of Bonna-7, Bonna-8 and Bonna-6.

Poisson’s impedance is a derived seismic attribute obtained from the combination of the values of P-impedance (AI) and S-impedance (SI). The Poisson’s impedance attribute result slice section is shown in Fig. 18. The PI attribute slice like other attributes (P-impedance, S-impedance, VP− VS ratio and density) generated for the Bonna field demarcates a probable reservoir zone around the well locations of Bonna-7, Bonna-8 and Bonna-6. A comparison of the PI result slice with other attributes (P-impedance, S-impedance, VP− VS ratio and density) sections derived from the pre-stack inversion reveals better delineation of the probable hydrocarbon saturated zone. As stated by Lantu et al. (2017), PI attribute is an important indicator for the identification of the existence of good hydrocarbon prospect. Much fluid saturation is observed around Bonna-6 well from the PI slice section when compared with the VP− VS ratio section (Fig. 16) indicating the sensitivity of the PI attribute over the VP− VS ratio in detecting the presence of fluid.

Further, inspection of the PI attribute slice reveals that there is a distinctive colour separation from the suspected hydrocarbon zone. These colour separation ranges moves from green to yellow and red to cyan. The green to yellow colour section is the wet zones saturated with hydrocarbon, while the red colour zone is the brine saturated area. Only the PI attribute gives a separation indicating the presence of brine sand (red colour), which is observed to appear immediately after the green to yellow zone. The shale zone in gold to cyan colour appears completely away from the zones inferred to harbour hydrocarbon and brine. This shale zone covers a major part of PI attribute slice with PI values ranging from \(5.2 \times 10^{3}\) to \(5.4 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). The PI attribute slice cross section clearly deciphers the hydrocarbon filled region in green to yellow colour with lower PI values ranging from \(4.9 \times 10^{3}\) to \(5.1 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). Also, the red colour zone interpreted to be brine filled sand region exhibits PI values ranging from \(5.2 \times 10^{3}\) to \(5.3 \times 10^{3} \;{\text{ft}}/{\text{s}}*{\text{g}}/{\text{cc}}\). The 3D view of the PI attribute is shown in Fig. 19. The figure depicts the areal spread of the delineated hydrocarbon and brine saturated zone within the shale region and location of the wells in Bonna field.

Fig. 19
figure 19

3D view of Poisson impedance attribute slice with inserted wells in Bonna field

Full size image

The root mean square (RMS) amplitude seismic attribute gives a measure of the energy in a loop or time. RMS attribute employed in seismic studies serves as a tool for the identification of prospective zones due to its sensitivity to direct hydrocarbon indication (DHI) and bright spot anomaly (Omoja and Obiekezie 2019). The RMS amplitude attribute slice obtained using a time window of 2234 ms is shown in Fig. 20. This attribute result is characterized with two major colours—red and blue. The red colour zones are the areas with high amplitude which corresponds to sand beds, while the low amplitude areas in blue colour are the shale bed zones. As stated by Hossain 2019, high amplitude troughs are an indicator of sands, while low amplitude represents shale beds. An inspection of the result reveals a high amplitude values of \(5.4 \times 10^{3}\) ms and \(3.7 \times 10^{3}\) ms around the well locations of Bonna-8 and Bonna-7, respectively. Also, an intermediate amplitude values of \(2.3 \times 10^{3}\) ms are observed around the well location of Bonna-6. The potential prospect area mapped using other attributes (P-impedance, S-impedance, density, VP− VS ratio and Poisson’s impedance) considered in this study corresponds to the zone with high amplitude in the RMS amplitude map results. This further ascertained that the mapped zone is hydrocarbon saturated region as increase high amplitude is synonymous to the presence of hydrocarbon. The RMS attribute has validated the various results presented in this study and reveals the significance of seismic inversion method of reservoir characterization.

Fig. 20
figure 20

Root mean square (RMS) amplitude seismic attribute

Full size image

Conclusion

The study has successfully delineated an area suspected to be hydrocarbon saturated sand reservoir in Bonna field. The delineated hydrocarbon zone appears low across the five (5) seismic attribute slices considered in this study. Although the delineated zone is deciphered to have values in attributes, which corresponds to hydrocarbon saturated reservoir, the PI attribute slice presents a good discrimination of the areal spread of the reservoir. PI attribute distinguishes the formation fluid into hydrocarbon filled sand, brine filled sand and shale zones. The PI attribute gives an improved delineation of the hydrocarbon reservoir over the other conventional seismic attributes (P-impedance, S-Impedance, VP− VS ratio and density) as it reveals better discrimination at the edges of the reservoir zone as given in the various results presented in the study area.