Stability and stable production limit of an oil production well

Abstract

Unstable well flow is detrimental to the technical and economic performances of an integrated production system. To mitigate this problem, it is imperative to understand the stability limits and predict the onset of unstable production of an oil well. Taking advantage of the phenomenon of slug flow and the onset of unstable equilibrium from inflow performance and vertical lift curves of a producing well, this paper presents a new method for evaluating the stability of an oil production well on the one hand and estimating its stable production limits in terms of wellhead flowing pressure and flow rate on the other hand. A novelty of this work is the introduction and quantitative characterization of three distinct stability phases in the performance of a production well. These phases are uniquely identified as stable, transition and unstable flows. Practical examples and field cases demonstrate the robustness of the new method. When compared against results from a commercial wellbore simulator for the same set of problems, the new method yields an average absolute deviation of 5.3%. Additional validation tests against a common, but more computationally demanding method of stability analysis yield satisfactory results. Several parametric tests conducted with the proposed model and method provide additional insights into some of the major factors that control well stability, highlighting scope for production optimization in practice. Overall, this work should find applications in the design and management of production wells.

Introduction

Recognizing the potential catastrophic impacts of compromised flow on the safety, environmental and economic performances of a project, flow assurance continues to generate interests in the upstream sector of the oil and gas industry (Alwazzan et al. 2019; Jamaluddin and Kabir 2012; Kaczmarski and Lorimer 2001). With respect to an integrated production system, the primary objective of flow assurance is to ensure the safe and economic delivery of produced hydrocarbons from the reservoir to the sales point. A key scope of a flow assurance study is a robust understanding of the potential vulnerability of the hydraulics of the production network (Alwazzan et al. 2019; Jamaluddin and Kabir 2012). In most cases, reservoirs and associated production wells are key components of a production network. Notwithstanding changes in the status and performances of the various subsystems in a network, ensuring optimum flow throughout the production lifetimes of a reservoir and its connected wells is one of the key deliverables of flow assurance in the exploration and production industry.

In terms of hydraulics, wells typically attract greater attention than reservoirs. This is partly because wells are more susceptible to the effects of declining pressure, especially as the asset ages. Typically, owing to its high hydrostatic head, most of the pressure losses experienced by a stream flowing from an oil reservoir to the sales point occur in the wellbore (Jamaluddin and Kabir 2012). In addition, being the link between subsurface and surface subsystems, the performance of a well remains crucial to guaranteeing the deliverability and optimum performance of the entire integrated system. Therefore, understanding the dynamics of a well and the stability limits of its flow is crucial to maximizing value from a production network.

To some extent, the hydraulic stability of a well is affected by pressure changes. These changes govern the prevailing flow regimes in a wellbore. For example, single-phase flow is achieved while the pressure exceeds the bubble point, while the bubble flow results with the distribution of small bubbles throughout the liquid phase when the prevailing pressure falls below the bubble point. While single phase, bubble and plug flow regimes are generally stable because of the associated high-pressure conditions, the onset of flow instability is typically represented by the slug flow regime, which emerges as a result of pressure decline beyond certain threshold (Douillet-Grellier et al. 2018; Jahanshahi et al. 2008; Sinegre et al. 2005, 2006; Blick et al. 1988). Further pressure decline may lead to annular and mist flow regimes, which aggravate the flow instability and consequent reduction in the liquid deliverability of an oil-producing well.

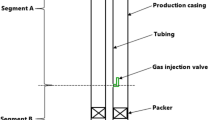
In principle, the stable production limit of an oil-producing well is defined by the wellhead flowing pressure (WHFP) at which the production becomes unstable (intermittent) due to the predominance of slug flow in the well. The slug flow regime is usually characterized by an intermittent two-phase flow pattern (Soedarmo et al. 2019; Douillet-Grellier et al. 2018), such that liquid slugs are separated by bullet-shaped gas pockets (Fig. 1). On a system performance plot (Fig. 2), unstable production is marked by a dual intersection of the inflow performance relationship (IPR) curve and the vertical lift performance (VLP) curve.

Fig. 1

Gas–liquid slug flow

Fig. 2

Performance plots of a well, illustrating the transition from stable production to dead state

With the VLP curves B or C shown in Fig. 2, the well is operating at unstable equilibrium. At a WHFP greater than or equal to the terminal WHFP (VLP curve D), the reservoir can no longer match the pressure required to assure flow through the tubing. At such conditions, the tubing behaves as a choke on the reservoir, leading to the cessation of flow in the well; hence, the well quits.

Unstable production is undesirable. In addition to causing formation damage and significant reduction in oil and gas production rates, a small perturbation in the system (e.g., fluctuations of separator pressure) may kill the well. Similarly, high momentum of the liquid slugs can damage pipe fittings such as elbows and tees, while slugs reduce the efficiency of separators. Furthermore, the resulting rate and pressure fluctuations degrade the performances of separators and other process vessels, in addition to causing the malfunctioning of sensors, transmitters and controllers. These effects increase the risks of emergency shutdown, as well as the attendant production deferments and value erosion (Lu et al. 2018; Mahdiani and Khamehchi 2015; Sinegre et al. 2005, 2006; Fairuzov et al. 2004; Perez and Kelkar 1990).

Despite its importance in defining the operating window of a well and its overall impact on the flow assurance of an integrated system, the determination of the onset of unstable equilibrium of an oil production well is not quite straightforward. The conventional method for predicting the stable production limit of an oil well is to use commercial wellbore modeling software to carry out sensitivity analysis on WHFP and identify the WHFP at which unstable flow (dual IPR–VLP intersection) begins. However, one shortcoming of this approach is its high computational costs, considering that several sensitivity tests are often required to establish the critical WHFP for flow instability. Another limitation of the current approach is that the transition between stable and unstable equilibrium conditions is not always well defined.

The commercial wellbore hydraulic simulators are not quite cheap, and their contributions to the operating expenses of a company are not always negligible. Hence, for executing this crucial task, there is a need for a method that is simple and accurate yet offering a reduced turnaround time. Furthermore, for improved asset management and value creation, we seek a better understanding, characterization and predictability of the transition between the stable and unstable flow states of a producing oil well.

Perhaps due to the popular applications of commercial wellbore hydraulic simulators to determine the onset of unstable production, the industry has developed only a handful of alternative methods. However, it is worthy of note that these alternative methods were developed primarily for the analysis of instability in gas-lifted wells (Jahanshahi et al. 2008; Sinegre et al. 2005, 2006; Blick et al. 1988). In gas-lifted wells, some researchers have attributed stability to the conditions that an increase in downhole tubing pressure results in a drop of mixture density and the casing pressure depletes faster than the tubing pressure (Asheim 1988).

Another definition of instability that is applicable to both naturally flowing and gas-lifted wells is attributed to heading (hydrodynamic instability), which is a flow regime characterized by regular and perhaps irregular cyclic changes in pressure at any point in a tubing (Sinegre et al. 2005; Fairuzov et al. 2004; Blick et al. 1988). In comparison with gas-lifted wells, it appears that the analysis and prediction of the stability of naturally flowing wells have attracted less attention. However, unlike wells that are under natural flow, the stability analysis of gas-lifted wells is quite complex and often requires transient multiphase flow simulations (Jahanshahi et al. 2008; Sinegre et al. 2005, 2006).

Although gas lifting generally improves well performance, it has been shown that gas lifting has a high tendency to cause flow instabilities, hence inducing production losses (Jahanshahi et al. 2008; Sinegre et al. 2005, 2006; Blick et al. 1988). Therefore, before considering activating gas lift, with its associated risks, as an option to improve well performance, it is imperative to fully understand the limits of stability under natural flow and maximize such knowledge for continuous value creation.

By accounting for the effects of pressure fluctuations on key well and reservoir parameters such as tubing inertance, tubing capacitance, wellbore storage and flow perturbation from the reservoir, Blick et al. (1988) derived a set of unsteady flow equations for naturally flowing and gas-lifted oil wells. By invoking the Laplace transform method and Cramer’s rule, they generated a characteristic equation from the unsteady flow equations. According to these authors, a well is stable when all the three coefficients of its characteristic equation are either positive or negative. Otherwise, the well is considered unstable. In practical terms, leveraging on the idea from control theory, Blick et al. (1988) argued that a well is stable when small flow transients from steady state decay with elapsed time, while instability is associated with an increase in small flow transients from steady state over time.

An obvious drawback of the method developed by Blick et al. (1988) is the complexity of the resulting characteristic equation and the attendant high computational costs of solving same. Although the Blick et al. (1988) model is suitable for both naturally flowing and gas-lifted oil wells, it was designed for only wells without production packer. However, from the standpoint of practical applications and proactive asset management, a major shortcoming of the method by Blick et al. (1988) is that, in contrast to the requirement of the IPR–VLP curve (Fig. 2), it does not provide the specific flow rate and WHFP at the onset of instability.

Jahanshahi et al. (2008) modified and combined the casing heading model (annulus model) and the density wave model (tubing model) proposed by Sinegre et al. (2005, 2006) to formulate a comprehensive description of instabilities due to gas lifting. However, their formulation is not without limitations. Its shortcomings include non-suitability for modeling naturally flowing oil wells, the complexity of its mathematical formulation that often requires expensive solution, and the non-provision for frictional losses in describing the hydraulics in the production tubing. As obtainable for Blick et al. (1988), another drawback of the technique by Jahanshahi et al. (2008) is its inability to provide the stable limits for a producing well in terms of specific flow rate and WHFP.

As an improvement over the conventional approaches that are time-consuming and characterized by high computational costs, this paper presents a simple and reliable method for evaluating the stability of naturally flowing oil production wells. More important, in line with the dictates of the IPR–VLP curves, the proposed method provides estimates of the stable production limits, which are the specific flow rate and WHFP at the onset of unstable equilibrium. This provision of the stability limits would facilitate better design and management of oil production wells for value creation and preservation. Considering some practical examples, sensitivity tests are conducted to demonstrate the applicability of the proposed method as well as to gain useful insights into the key controls of stability and stable production window of an oil well. As a further validation test, for the same set of problems, the performance of the proposed method is evaluated against that of Blick et al. (1988), which is a common method of stability analysis.

Model formulation

In principle, both stable and unstable conditions are manifestations of the performance of a production system. Therefore, to understand the stability limits of an oil production well, it is logical to build a reliable well performance model. To overcome the limitations of the established models, we are proposing a simple model which accounts for the relevant flow physics in the well/reservoir system, as illustrated in Fig. 3. For simplicity, it is assumed that the complex heterogeneous flow in the said system can be approximated as semi-homogenous with appropriate average fluid mixture properties.

Fig. 3

Pressures and temperatures at key nodes in a producing system

Taking the top of the drainage interval as the solution node (Fig. 3), the inflow performance of the pseudo-steady or steady system is described by the following expression:

$$P_{\text{wf}} = \overline{{P_{\text{r}} }} - \frac{{Q_{\text{L}} }}{{J_{\text{L}} }}.$$

(1)

The definitions and units of the quantities in Eq. 1 and other equations in this paper are presented in the list of symbols.

With the assumption that the acceleration pressure loss is negligible, the outflow performance is derived from the Bernoulli’s equation as follows:

$$P_{\text{wf}} = \frac{{32f_{\text{F}} \overline{{\rho_{\text{m}} }} LQ_{\text{m}}^{2} }}{{\pi^{2} D^{5} }} + \overline{{\rho_{\text{m}} }} gh + P_{\text{wh}} .$$

(2)

The first and second terms on the right-hand side of Eq. 2 represent the frictional and gravitational pressure losses, respectively. It can be shown that the flow in a typical well is turbulent. For example, a well with a tubing inner diameter of 3.958 in, production rate of 5000 STB/d, mixture viscosity of 0.4 cP and mixture density of 43.7 lb/f³ has a Reynolds number of about 2 × 10⁵, which is roughly one hundred times the threshold (2100) of turbulent flow. As a result, subsequent treatments in this study assume that fluid flow in a production tubing is always turbulent.

With the understanding that the flow in the tubing is often turbulent, we apply the following Blasius correlation for friction factor (Lampinen et al. 2001):

$$f_{\text{F}} = 0.071625\left( {\frac{{\mu_{\text{m}} D}}{{\overline{{\rho_{\text{m}} }} Q_{\text{m}} }}} \right)^{0.25} .$$

(3)

At the operating (equilibrium) point of the system, the inflow and outflow performances are equal. Thus, by combining Eqs. 1 and 2, while expressing the variables in field units, we obtain the following equation:

$$\left( {\frac{{3.4834 \times 10^{ - 16} LM^{\prime 2} }}{{\overline{{\rho_{\text{m}} }} D^{5} }}} \right)Q_{\text{LS}}^{2} + \frac{1}{{J_{\text{L}} }}Q_{\text{LS}} + \left( {P_{\text{wh}} + \frac{{\overline{{\rho_{\text{m}} }} h}}{144} - \overline{{P_{\text{r}} }} } \right) = 0,$$

(4)

where we define the mass of mixture associated with a unit volume of liquid as follows:

$$M^{\prime } = 350.5\left[ {\gamma_{\text{o}} (1 - f_{\text{w}} ) + \gamma_{\text{w}} f_{\text{w}} } \right] + R_{\text{p}} \rho_{\text{a}} \gamma_{\text{g}} (1 - f_{\text{w}} ).$$

(5)

The resulting equilibrium equation (Eq. 4) is a quadratic, with the solution presented in Eq. 6. In principle, the positive root of this quadratic equation yields the “stabilized” (or equilibrium) liquid production rate, Q_LS. The method and correlations used to estimate the average mixture density (ρ_m) are discussed in “Appendix A.”

$$Q_{\text{LS}} = \frac{{ - b + \sqrt {b^{2} - 4ac} }}{2a},$$

(6)

where

$$a = \left( {\frac{{3.4834 \times 10^{ - 16} LM^{\prime 2} }}{{\overline{{\rho_{\text{m}} }} D^{5} }}} \right),$$

(7)

$$b = \frac{1}{{J_{\text{L}} }},$$

(8)

$$c = \left( {P_{\text{wh}} + \frac{{\overline{{\rho_{\text{m}} }} h}}{144} - \overline{{P_{\text{r}} }} } \right).$$

(9)

Before applying the foregoing models to identify the onset of unstable production, it is necessary to validate its performance. We use PIPESIM, which is a commercial wellbore simulator developed by Schlumberger, for model validation in this case. Three different oil production wells are considered as test examples. Table 1 summarizes the set of well, reservoir and fluid data used for the example wells A, B and C in both PIPESIM and our equilibrium model (Eq. 6). The results (P_wh vs. Q_LS) obtained from both models are compared.

Table 1 Input datasets, for example wells

It should be noted that the PIPESIM models in these case examples incorporate the Hagedorn and Brown (1965) VLP correlation, which is a rigorous separated-flow correlation. Figures 4, 5 and 6 present the performance plots for the individual example wells. From these results, it is evident that there is good agreement (< 3% deviation) between PIPESIM and the new model, even though the latter ignores liquid holdup (separated flow) in its formulation.

Fig. 4

Comparison of models for well A

Fig. 5

Comparison of models for well B

Fig. 6

Comparison of models for well C

Stability and stable production limit

Following a close examination of Figs. 4, 5 and 6, one can deduce the following points:

• 1. Stabilized flow rate varies inversely with WHFP, but the dependency is nonlinear

• 2. As WHFP increases, stabilized production rate becomes more sensitive to WHFP. In other words, the absolute value of dQ_LS/dP_wh increases as P_wh increases.

As a result of the foregoing deductions (especially the second point), the following questions are pertinent.

• What can a plot of |dQ_LS/dP_wh| versus P_wh tell us about the behavior of a well?

• By analyzing this behavior, can we establish (uniquely) the stable production limit (i.e., onset of unstable equilibrium) of the well at prevailing conditions of the reservoir–well system?

To answer the preceding questions, well A is used as a case study and the following steps are applied.

• 1. Rewrite the new well performance model (Eq. 4) in the form, $P_{\text{wh}} = f\left( {Q_{\text{LS}} } \right) = \, AQ_{\text{LS}}^{2} + BQ_{\text{LS}} + \, C$ and derive ${\text{d}}P_{\text{wh}} /{\text{d}}Q_{\text{LS}} = \, 2AQ_{\text{LS}} + B$. In this expression, A = −a, B = −b and C = P_wh − c. The quantities a, b and c are the coefficients in Eq. 4.

• 2. Invert dP_wh/dQ_LS to obtain ${\text{d}}Q_{\text{LS}} /{\text{d}}P_{\text{wh}} = 1/(2AQ_{\text{LS}} + B)$. Refer to “Appendix B” for a proof of the validity of this simple inversion.

• 3. For a set of different P_wh, generate the corresponding set of Q_LS per Eqs. 6–9.

• 4. For the same set of P_wh versus Q_LS, construct the stability plot at prevailing reservoir and wellbore conditions as $\left| {{\text{d}}Q_{\text{LS}} /{\text{d}}P_{\text{wh}} } \right| \, = \, \left| {1/\left( {2AQ_{\text{LS}} + B} \right)} \right|$ versus P_wh. For production wells, because of the inverse relationship between Q_LS and P_wh, the quantity ${\text{d}}Q_{\text{LS}} /{\text{d}}P_{\text{wh}}$ is always negative. Thus, for visual convenience, the magnitude of this quantity is considered in this work.

• 5. Based on the above plot, identify the various production stability phases, as suggested by differences in curves and slopes (see the next section).

The foregoing steps outline how to generate the required performance dataset of P_wh versus Q_Ls from Eq. 4 and describe how to construct the stability plot from the same dataset. We refer to the full combination of these steps as the new model and new procedure.

However, we recognize the availability of other methods of generating the performance dataset of FWHP versus flow rate. Where such methods are used, we still need to implement a procedure to construct the stability plot from such dataset. In such a case, we offer the following steps. We refer to the full combination of these steps as the old model and new procedure.

• 1. Generate performance dataset (WHFP vs. rate) from a suitable source, such as PIPESIM (e.g., Fig. 4)

• 2. Fit a quadratic function to the WHFP versus rate dataset and obtain the empirical regression equation, $P_{\text{wh}} = f\left( {Q_{\text{LS}} } \right) = \, pQ_{\text{LS}}^{2} + qQ_{\text{LS}} + r$, and derive ${\text{d}}P_{\text{wh}} /{\text{d}}Q_{\text{LS}} = 2pQ_{\text{LS}} + q$. The quantities p, q and r are empirical constants

• 3. Invert dP_wh/dQ_LS to obtain ${\text{d}}Q_{\text{LS}} /{\text{d}}P_{\text{wh}} = 1/(2pQ_{\text{LS}} + q)$

• 4. For a set of different P_wh, generate the corresponding set of Q_LS per the function in step 2

• 5. Execute steps 4 and 5 as described earlier under new model and new procedure.

Stability phases

To make this process clearer, we demonstrate with an example. It is worth highlighting that the quantity |dQ_LS/dP_wh| describes the system’s response to fluctuating WHFP. Upon plotting |dQ_LS/dP_wh| versus P_wh for the example well A, Fig. 7 shows that three distinct phases can be identified. The following are the physical interpretations of these phases and the phenomena at play.

Fig. 7

Stability plot for well A based on the new model and new procedure

• Phase I In this phase, production is stable. Hence, the rate of change of stabilized production rate with respect to WHFP is minimal. That is, the system’s response to fluctuating WHFP is gentle (not necessarily constant) and virtually linear. Mathematically, slope of the |dQ_LS/dP_wh| versus P_wh curve is finite, but close to zero in this region (Fig. 7)

• Phase II This is the transition phase, in which production exhibits some increasing instability. Hence, the stabilized production rate is very sensitive to WHFP in this phase. Essentially, the system’s response to fluctuating WHFP becomes a pronounced curve. Mathematically, slope of the |dQ_LS/dP_wh| versus P_wh curve is nonzero, but a relatively small positive value in this region (Fig. 7)

• Phase III In this phase, the well is dying, thus the exponential change in production rate when the WHFP changes. Mathematically, slope of the |dQ_LS/dP_wh| versus P_wh curve returns a very large positive value in this region (Fig. 7).

Given the descriptions of the stability phases, the identifier for the stable production limit is the point of intersection between the stable (linear) and the transition (curved) regions.

In this example case illustrated in Fig. 7, a combination of the new model and new procedure predicts that unstable production begins at a WHFP of ~ 800 psia. As shown in Fig. 8, the well behavior plot based on the PIPESIM results and our new procedure also indicates that ~ 800 psia is the stable production limit for this well under the same conditions. Note that the reported ~ 800 psia attributed to PIPESIM was not generated directly by PIPESIM. But it was obtained by submitting PIPESIM-generated WHFP versus rate performance data (Fig. 4) to our new method of stability analysis and plot as described in earlier section and Fig. 7. Although PIPESIM did not report out its stable limit, it is interesting to note that our foregoing results agree with the ~ 750 psia that was observed (through visual inspection) in the PIPESIM output. The well behavior plots for the other wells are displayed in Figs. 9 and 10 for wells B and C, respectively. In all cases, results of the new model + new procedure and PIPESIM + new procedure are generally comparable.

Fig. 8

Stability plot for well A, after applying the new procedure to the performance data generated from the PIPESIM model

Fig. 9

Stability plots for well B

Fig. 10

Stability plots for well C

Table 2 summarizes the results for all the wells considered in this study. In all the cases investigated, there is excellent agreement (i.e., average absolute deviation of about 5%) between our new method and PIPESIM. Note that we deliberately evaluated the deviation of our new method (column 4 in Table 2) against the corresponding PIPESIM results (column 2). Ideally, the former should have been compared against column 3, which would have returned perfect agreements between our new method and “corrected” PIPESIM results.

Table 2 Stable production limits from different models and methods for the example wells

For clarity, we need to explain the column titled “PIPESIM results + new procedure” in Table 2. This refers to results obtained when we submitted the PIPESIM-generated (with separated-flow VLP correlation) dataset of WHFP versus flow rate to our new procedure of stability analysis. On the other hand, the column titled “new model results + new procedure” presents results obtained by strict applications of our new stability analysis to the P_wh versus Q_Ls dataset generated by our new performance model (without separated-flow VLP correlation) in Eqs. 4–9. The column titled “PIPESIM software” provides the results inferred strictly from PIPESIM without applying our stability procedure.

Following a close examination of the results in columns 2, 3 and 4 in Table 2, the following deductions are noteworthy:

• The method of estimating production stability limit in PIPESIM and our new proposal are different

• For the same set of input parameters, there is excellent agreement in the performance curves (P_wh vs. Q_Ls) generated by PIPESIM (with separated-flow VLP correlation) and our simple model (without separated-flow VLP correlation)

• On submitting PIPESIM-generated performance dataset to our new stability procedure, there is excellent agreement between PIPESIM and our new method of determining stability and stable production limits of oil production wells

• The strict application of our new method (models and procedures) to generate performance curves, conduct stability analysis and establish stability limits of an oil production well is robust and yields satisfactory results

Sensitivity tests

To further quality-check this new method, the new model was applied to the same well A, but in this case, with a water cut (fraction) of 0.30. In the previous analyses, the water cut (fraction) was 0.0. As shown in Fig. 11, when the water cut increases, the well still demonstrates the stable, transition and dying regions, i.e., phases I, II and III, respectively. However, as expected, the lifting potential of the well reduces as its water cut increases. Hence, when the water cut (fraction) increases from 0.0 to 0.30, the stable production WHFP limit decreases from ~ 800 psia (12,437 STB/d) to ~ 600 psia (14,859 STB/d).

Fig. 11

Stability plots for well A at different water cuts

It is instructive to note that, while the stable production WHFP limit is an upper bound, its corresponding flow rate is a lower bound. This is because flow rate varies inversely with WHFP. Essentially, a reduced stable production limit (lower WHFP) means a smaller stability window (higher flow rate), and vice versa. A smaller stability window implies that the well risks being unstable (i.e., slugging) at a higher flow rate. In other words, at the same flow rate, a well with a smaller stability window would exhibit greater instabilities than its counterpart with a larger stability window. Thus, from an offtake standpoint, these simulation results suggest that the 30% water cut reduces the stability window by about 19%. In both examples, the well remained on natural flow. These results explain the common field observation of increased instability as the water cut of a well rises.

For greater insights, we examine the impacts of gas lift (or gas-cap breakthrough) on production limit. For the same case of 30% water cut, the effect of active GOR on the performance of well A was examined with our new model. Figure 12 compares the results of low and high GOR scenarios. It is worthy of note that the low and high GOR cases are characterized by active wellbore GOR of 476 and 1428 SCF/STB, respectively. Figure 12 shows that, when the well transits from the low to high GOR state, its stable production limit increases from ~ 600 psia (14,859 STB/d) to ~ 1100 psia (11,393 STB/d). Thus, higher GOR gives the well more “freedom” to produce stably. This improvement is not unexpected, considering that gas enhances the production of oil wells by reducing the hydrostatic head through the lightening of the column of fluids in the wellbore. In other words, this example shows that the execution of gas lifting or the breakthrough of gas cap has the potential to help the well overcome a backpressure of as much as 1100 psia at the well head, as against just 600 psia while operating at low active GOR, thereby increasing the window of stable production (i.e., ability to produce at lower offtake rates without experiencing instability) by about 23%.

Fig. 12

Stability plots for well A at 30% water cut, but different active GOR

To understand the effects of reservoir depletion on the limits of stable production, Fig. 13 illustrates the stability performance curves for three different cases of reservoir pressure, P_r. As the reservoir pressure declines from 2817 to 2305 psia, the stable production limit decreases from ~ 800 psia (13,150 STB/d) to ~ 400 psia (14,276 STB/d). These results clearly demonstrate that an oil production well becomes increasingly more likely to die due to flow instability in the wellbore as the reservoir’s drive energy becomes weaker. These results provide additional insights into the typical underperformance of production wells in mature reservoirs, especially at late life.

Fig. 13

Stability plots for well A at 30% water cut, but different reservoir pressures

Furthermore, we interrogate the proposed method by sensitizing on the tubing inner diameter (ID). As shown in Fig. 14, as the tubing ID is reduced from 0.3298 to 0.2897 to 0.2292 ft, phase I gets flatter. Accordingly, the stable production limit increases from ~ 550 to ~ 600 to ~ 700 psia, respectively. In terms of flow rate, the attendant onset of unstable equilibrium reduces from ~ 14,859 to 10,105 to 4588 STB/d, respectively, suggesting increasing stability window as the tubing becomes smaller.

Fig. 14

Stability plots for well A at 30% water cut and P_r = 2561 psia, but different tubing sizes

Smaller tubing IDs favor vertical lift due to the capillary effect (pro-stability), in which capillary rise and particle-carrying capacity vary inversely with the tubing ID. On the other hand, smaller tubing IDs are more restrictive to flow due to the choking effect (anti-stability), whereby entry efficiency and frictional losses are proportional and indirectly proportional to tubing ID, respectively. Our results show that, from the standpoint of impacting flow stability, the capillary effect dominates the choking effect. Thus, the stable production limit varies inversely with tubing ID. These results are corroborated by field experience, since we know that wells with larger tubing IDs are more prone to unstable production than their smaller ID counterparts, under similar conditions. Furthermore, these results partly support the occasional field practice, especially in mature assets, of replacing a larger tubing with a smaller one to improve the stability and extend the active lifetime of a producing well (Blick et al. 1988). The relationship between conduit size and system stability deserves further study. As demonstrated by Inok et al. (2019), placing a venturi in the horizontal topside section also improves system stability substantially.

As additional robustness checks, we conduct further validation tests on the new method by applying a more demanding and computationally intensive method (Blick et al. 1988) to wells A, B and C. Table 3 presents relevant datasets (in addition to the ones in Table 1) required by the Blick et al. (1988) model as well as the results from our new method and the Blick et al. (1988) model.

Table 3 Other input datasets required to evaluate the stability of wells A, B and C by the method of Blick et al. (1988)

In Table 3, the P_wh and Q_LS pairs are datapoints on the appropriate P_wh versus Q_LS curves of the new model (Figs. 4, 5, 6), while the P_wh* and Q_LS* pairs are the stability limits determined by our new method. Clearly, our new method indicates that wells A, B and C are stable (i.e., P_wh < P_wh* and Q_LS > Q_LS*) at the indicated P_wh and Q_LS pairs.

Using the same dataset and the specified P_wh–Q_LS operating points, application of the stability method of Blick et al. (1988) returns positive values of the characteristic parameters K₁, K₂ and K₃ for the individual wells. According to Blick et al. (1988), a well is said to be stable at a given operating point if all these three characteristic parameters have the same sign. Therefore, in this case, it is conclusive that our method agrees with that of Blick et al. (1988) that the three wells are stable at the specified P_wh–Q_LS operating points.

Further validation of the proposed model and procedure

To confirm the efficacy of the proposed model and procedure, we consider the oil production well V2-B, completed in reservoir V2 in a field within the swamp area of the Niger Delta basin. V2 is an oil rim reservoir, characterized by an initial oil thickness of 25 ft and developed by six wells with production history. At the time the reservoir was placed off stream, it had achieved an oil recovery factor of 27% after 33 years of production. The first well quit on high GOR and water cut (WCT). Four wells, including V2-B, were closed-in due to high water cut (HWCT) and flow instability, while the sixth well was closed-in for high GOR.

V2-B is a vertical well with a 4-ft perforation interval in V2. The perforation top is 17 ft away from the original gas–oil contact, while the perforation base is 4 ft away from the original oil–water contact. V2-B came onstream in 1982 and produced dry until 1987—the same year its GOR began to rise. Sometime in 1992, both the GOR and WCT peaked. The well was then beaned back to mitigate the problems associated with gas and water production. While the GOR remained largely curtailed, the WCT was less impacted owing to the strong aquifer and its proximity to the perforation. Figures 15 and 16 display the performances of V2-B.

Fig. 15

Liquid and gas rates production history of well V2-B

Fig. 16

Production ratios history of well V2-B

With the data in Table 4, we calculate |dQ_LS/dP_wh| for a set of different P_wh and construct the stability plots for V2-B at two different times. These time vintages are (1) in 1991, when it was stable; and (2) in 2004, when it was unstable. As shown in Fig. 17, at the reference point in 1991, the stability limit was ~ 1200 psia. Therefore, as expected, with a WHFP of 1010 psia, the well was stable at the given conditions. At the reference point in 2004, the stable (linear) region is practically absent. Unsurprisingly, the well was inherently unstable under the reported conditions at that time. In addition to the outcome of the prior tests conducted with the field cases reported in Blick et al. (1988), this example from the Niger Delta further confirms the simplicity, robustness and applicability of the new method of evaluating the stability and stable production limits of oil production wells.

Table 4 Relevant data of well V2-B

Fig. 17

Stability plots for well V2-B, showing significant degradation of stability between 1991 and 2004

Conclusion

Taking advantage of the phenomenon of slug flow and the onset of unstable equilibrium from IPR and VLP curves, a new method for evaluating both the stability and stable production limit of an oil production well has been presented and validated. With an AAD of 5.3%, the validation tests demonstrate the robustness of the method. Practical examples, parametric tests and field case studies provide useful insights into some of the major factors that control well stability, and the scope for production optimization.

In addition to the other contributions of this study to the current body of knowledge on the modeling and management of well performance, one major novelty of this work is the introduction and quantitative characterization of three distinct stability phases in the evaluation of the performance of a production well. These phases are stable, transition and unstable flow regions. As an improvement in existing methods that only provide indication of the stability window, the new method quantifies the stability limits in terms of both WHFP and flow rate.

In addition to the introduction and definition of the above stability phases, this work has successfully developed and validated a quantitative and definitive technique to identify these phases with less ambiguity. Further tests with another stability model confirm the validity of the new method. This work is considered a useful addition to the existing set of tools for the design and management of oil and gas assets in general, but production wells particularly.

Notwithstanding the satisfactory performances and simplicity of the proposed method, there are areas of improvement. Future focus areas include the consideration of highly volatile oil reservoirs and production below bubble-point pressure, in which the productivity index may be very sensitive to pressure. Other focus area is the extension of this work to gas-lifted wells, especially their stability analysis under transient conditions.

Appendices

Appendix A: Estimating the average mixture density within wellbore

The average mixture density is calculated with the following formula:

$$\overline{{\rho_{\text{m}} }} = \frac{{M^{\prime } }}{{\overline{{V_{\text{m}}^{\prime } }} }}.$$

(10)

The average in situ mixture volume associated with 1 STB of liquid is given by

$$\begin{aligned} \overline{{V_{\text{m}}^{\prime } }} &= 5.615\left[ {\overline{{B_{\text{o}} }} (1 - f_{\text{w}} ) + \overline{{B_{\text{w}} }} f_{\text{w}} } \right]\\&\quad + \left[ {\left( {R_{\text{p}} - \overline{{R_{\text{s}} }} } \right)(1 - f_{\text{w}} )\left( {\frac{{0.02827(\overline{T} + 460)\overline{z} }}{{\overline{P} }}} \right)} \right]. \end{aligned}$$

(11)

As indicated in Eq. 11, simplicity warrants using the average temperature and pressure between the wellhead and bottomhole to calculate the relevant fluid properties such as average oil formation volume factor, average solution gas–oil ratio, average gas compressibility and, by extension, the average mixture density in the well. The average water formation volume factor is assumed to be 1 bbl/STB.

In the present work, estimates of B_o, R_s and z are obtained from the empirical correlations Standing (1952) and Lasater (1958) as well as Yarborough and Hall (1974), respectively.

Appendix B: Proof of dx/dy = 1/(dy/dx) for general functions

Although the proof presented here can, in principle, readily be extended to any function, we limit our current interest to quadratic functions. The choice of a quadratic function is in line with the form of our production stability equation (i.e., Eq. 4).

The general form of quadratic functions is

$$y = f(x) = Ax^{2} + Bx + C,$$

(12)

where the quantities A, B and C are constants.

Assuming f(x) is a continuous and differentiable function.

$$\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2Ax + B.$$

(13)

The inverse function, x = g(y) is derived as follows, after recasting Eq. 12.

$$Ax^{2} + Bx - (y - C) = 0.$$

(14)

Solving Eq. 14 for x, i.e., g(y), yields the following expression:

$$x = g(y) = \frac{{ - B \pm \sqrt {B^{2} + 4A(y - C)} }}{2A}.$$

(15)

Equation 15 is the inverse function of Eq. 12. For mathematical convenience, Eq. 15 can be rewritten as follows:

$$x = - \frac{B}{2A} + m,$$

(16)

in which

$$m = \pm \frac{{n^{1/2} }}{2A},$$

(17)

and

$$n = B^{2} + 4A(y - C).$$

(18)

dx/dy can be found by applying the chain rule of differentiation to Eqs. 16–18, i.e., Eq. 19, to yield Eq. 20.

$$\frac{{{\text{d}}x}}{{{\text{d}}y}} = \frac{{{\text{d}}x}}{{{\text{d}}m}} \times \frac{{{\text{d}}m}}{{{\text{d}}n}} \times \frac{{{\text{d}}n}}{{{\text{d}}y}} .$$

(19)

$${\therefore }\frac{{\text{d}x}}{{\text{d}y}} = {1 \times }\left( {{ \pm }\frac{\text{1}}{{\text{4}An^{{\text{1/2}}} }}} \right) \times \text{4}A{ = \pm }\frac{\text{1}}{{\sqrt {B^{\text{2}} + \text{4}A(y - C)} }}\text{.}$$

(20)

To break down B² + 4A(y − C), replace y with the right-hand side of Eq. 12 to obtain

$$B^{2} + 4A(y - C) = 4A^{2} x^{2} + 4ABx + B^{2} .$$

(21)

Through factorization, it can be shown that

$$B^{2} + 4A(y - C) = 4A^{2} x^{2} + 4ABx + B^{2} = (2Ax + B)^{2} .$$

(22)

Therefore, from Eq. 20, we have

$$\frac{{\text{d}x}}{{\text{d}y}}{ = \pm }\frac{\text{1}}{{\text{(2}Ax\text{ + }B\text{)}}}\text{.}$$

(23)

It is noteworthy that the absolute value of the right-hand side of Eq. 23 equals the absolute value of the reciprocal of the right-hand side of Eq. 13. As shown in Fig. 18, when the axes are flipped, the absolute value of the slope at a given point might change, but the sign (positive or negative) remains the same. In other words, dy/dx and dx/dy must have the same sign.

Fig. 18

Schematics of slopes at arbitrary points (x_o, y_o) and (y_o, x_o) on y = f(x) and x = g(y) curves, respectively

Therefore, for the general quadratic function examined, we have established that the following expression is valid.

$$\frac{{\text{d}x}}{{\text{d}y}} = \frac{\text{1}}{{\text{(d}y\text{/d}x\text{)}}} = \frac{\text{1}}{{\text{(2}Ax\text{ + }B\text{)}}}\text{.}$$

(24)

Considering that our production stability equation P_wh = f(Q_LS) is of quadratic form, and a subset of the general form of Eq. 12, we therefore confirm the validity of the following expression as used in our current work.

$$\frac{{{\text{d}}Q_{\text{LS}} }}{{{\text{d}}P_{\text{wh}} }} = \frac{1}{{({\text{d}}P_{\text{wh}} /{\text{d}}Q_{\text{LS}} )}}.$$

(25)