Introduction

The prediction of shale gas production rates and volumes is an important part of oilfield development (Elmabrouk et al. 2014). Whether the production of shale gas wells can be predicted effectively in the future, based on the historical data, is related to the real-time adjustment of the shale gas well working schedule, thus playing the role of an assistant during decision-making (Mohammadpoor and Torabi 2018).

There are three methods to predict production rate. First is the reservoir engineering method based on basic percolation theory, for example, production decline analysis (Bahadori 2012; Miao et al. 2020; Wang 2017). This method takes into account the effects of reservoir properties, well conditions, and production control parameters on shale gas production. It is a common mathematical statistics method for predicting and analysing reservoir production performance and is one of the typical representations used in shale gas field. However, the reservoir engineering criteria are obtained for an ideal percolation environment, which will not reflect fully the phenomena and laws of actual shale gas field percolation. Furthermore, during operation, shale gas production is constantly being interfered with by various stimulation technologies (Luo et al. 2019), such as fracturing and acidizing, and the production decline analysis has certain limitations.

The second prediction approach includes the numerical simulation methods (Ado et al. 2019). This approach has high reliability, but it needs a clear understanding of geological conditions and the reservoir condition. From model building, to historical fitting, to development prediction, the whole process is long and complex, and the procedure is difficult. A third option utilizes machine learning methods based on data mining, such as grey system theory (Hu et al. 2018; Hu 2020; Julong 1982; Qiao et al. 2019; Yang et al. 2015; Ye et al. 2020; Zhou et al. 2019b), and artificial neural networks (Khan et al. 2020; Seyyedattar et al. 2020; Xiong and Lee 2020; Yang et al. 2005). Compared with the traditional methods, machine learning has a lower reliance upon the hypothetical data. It mines the actual data deeply by setting training sets and verifies the generalization ability of the model through independent verification sets. Therefore, especially in the case of large amounts of data, machine learning often has excellent prediction performance (Goebel et al. 2020; Ma 2019).

As the physical parameters of a reservoir are uncertain and complex, and such geological and engineering parameters are difficult to obtain (Luo et al. 2020), it is very difficult to predict shale gas well production by the use of reservoir engineering methods and numerical simulation methods. However, machine learning methods, especially grey system theory, have played an important role in predicting shale gas production (Ma and Liu 2016). Although grey system theory has good performance in solving small sample problems, it still has some limitations in application; for example, the calculation of background values has errors. In order to solve these problems, some researchers have deduced the accurate background value of the GM(1, 1) model by using the solution for non-homogeneous forms (Truong and Ahn 2012a, b; Zhou et al. 2019a). Because of the validity of the background value transformation method, many scholars have begun to transform the background value of other grey system models, such as the grey power model, the grey Verhulst model (Rajesh 2019), the discrete non-homogeneous model (Cui et al. 2013), and the multivariable grey prediction model (Zhi et al. 2017). These models have developed forecasting theory to a certain extent, but there are still some problems. For example, the optimization of background values is unreasonable, and the data are not processed smoothly.

The present investigation focused upon the cause of error in the existing conventional GM(1, N) model, taking the production of shale gas wells as the research object and establishing an improved GM(1, N) model-based shale gas well productivity prediction model. To achieve this, firstly the original data were smoothed. Secondly, the improved GM(1, N) model was established, based on improving the background value of the existing conventional GM(1, N) model. Finally, the model established during the present study was compared and analysed through the example calculation.

Methodology

GM(1, N) is one of the main methods of grey system theory and is a first-order differential equation composed of multivariables. It mainly fits and predicts the dominant factors and related variables in some complex systems under the condition of “small sample and poor information”.

The principles of GM(1, N)

The feature series (or output series) is (Julong 1982):

$$X_{1}^{(0)} { = }\left\{ {x_{1}^{(0)} \left( 1 \right),x_{1}^{(0)} \left( 2 \right), \ldots x_{1}^{(0)} \left( n \right)} \right\}.$$
(1)

The sequence of related factors is (Tien 2011):

$$\begin{gathered} X_{2}^{(0)} { = }\left\{ {x_{2}^{(0)} \left( 1 \right),x_{2}^{(0)} \left( 2 \right), \ldots x_{2}^{(0)} \left( n \right)} \right\} \hfill \\ X_{3}^{(0)} { = }\left\{ {x_{3}^{(0)} \left( 1 \right),x_{3}^{(0)} \left( 2 \right), \ldots x_{3}^{(0)} \left( n \right)} \right\} \hfill \\ \cdot \cdot \cdot \hfill \\ X_{N}^{(0)} { = }\left\{ {x_{N}^{(0)} \left( 1 \right),x_{N}^{(0)} \left( 2 \right), \ldots x_{N}^{(0)} \left( n \right)} \right\}. \hfill \\ \end{gathered}$$
(2)

\(X_{i}^{\left( 1 \right)}\) is the 1-AGO sequence of \(X_{i}^{\left( 0 \right)}\), and

$$x_{i}^{(1)} \left( k \right) = \sum\limits_{j = 1}^{k} {x_{i}^{(0)} \left( j \right)} , \, k = 1,2, \ldots n.$$
(3)

The equal weight mean value sequence of \(X_{1}^{\left( 1 \right)}\), \(Z_{1}^{\left( 1 \right)}\), is:

$$Z_{1}^{(1)} { = }\left\{ {z_{1}^{(1)} \left( 1 \right),z_{1}^{(1)} \left( 2 \right), \ldots z_{1}^{(1)} \left( n \right)} \right\}$$
(4)

where,

$$z_{1}^{(1)} \left( k \right){ = }0.5x_{1}^{(1)} \left( k \right) + 0.5x_{1}^{(1)} \left( {k - 1} \right), \, k = 2,3, \ldots ,n.$$
(5)

The grey differential equation is:

$$x_{1}^{(0)} \left( k \right) + az_{1}^{(1)} \left( k \right) = \sum\limits_{i = 2}^{n} {b_{i} } x_{i}^{(1)} \left( k \right)$$
(6)

where \(x_{1}^{(0)} \left( k \right)\) is the grey derivative, \(z_{1}^{(1)} \left( k \right)\) is the background value, \(a\) is the developing coefficient, and \(b\) is the grey action quantity.

Then, the whitening differential equation of GM(1, N) is:

$$\frac{{{\text{d}}x_{1}^{(1)} \left( t \right)}}{{{\text{d}}t}} + ax_{1}^{(1)} \left( t \right) = \sum\limits_{i = 2}^{n} {b_{i} } x_{i}^{(1)} \left( t \right).$$
(7)

If the range of \(x_{i}^{(1)} \, \left( {i = 1,2, \ldots n} \right)\) is not too wide and \(\sum\limits_{i = 2}^{n} {b_{i} } x_{i}^{(1)} \left( k \right)\) is a grey constant, then:

$$\widehat{x}_{1}^{(1)} \left( {k + 1} \right) = \left[ {x_{1}^{(1)} \left( 0 \right) - \frac{1}{a}\sum\limits_{i = 2}^{n} {b_{i} } x_{i}^{(1)} \left( {k + 1} \right)} \right]e^{ - ak} { + }\frac{1}{a}\sum\limits_{i = 2}^{n} {b_{i} } x_{i}^{(1)} \left( {k + 1} \right).$$
(8)

Finally, the predicted value of the feature series is obtained by cumulative subtraction:

$$\widehat{x}_{1}^{(0)} \left( {k + 1} \right) = \widehat{x}_{1}^{(1)} \left( {k + 1} \right) - \widehat{x}_{1}^{(1)} \left( k \right).$$
(9)

The least-square estimation of the parameters of GM(1, N), \(\left[ {a,b_{2} , \cdot \cdot \cdot ,b_{n} } \right]^{T}\), satisfies:

$$\left[ {a,b_{2} , \ldots ,b_{n} } \right]^{T} { = }\left( {B^{T} B} \right)^{ - 1} B^{T} Y_{R}$$
(10)

where

$$B = \left[ \begin{gathered} - z^{(1)} \left( 2 \right) \, x_{2}^{(1)} \left( 2 \right) \, \cdot \cdot \cdot \, x_{n}^{(1)} \left( 2 \right) \hfill \\ - z^{(1)} \left( 3 \right) \, x_{2}^{(1)} \left( 3 \right) \, \cdot \cdot \cdot \, x_{n}^{(1)} \left( 3 \right) \hfill \\ \cdot \cdot \cdot \hfill \\ - z^{(1)} \left( n \right) \, x_{2}^{(1)} \left( n \right) \, \cdot \cdot \cdot \, x_{n}^{(1)} \left( n \right) \hfill \\ \end{gathered} \right],Y_{R} { = }\left[ \begin{gathered} x_{1}^{(0)} \left( 2 \right) \hfill \\ x_{1}^{(0)} \left( 3 \right) \hfill \\ \hfill \\ x_{1}^{(0)} \left( n \right) \hfill \\ \end{gathered} \right].$$
(11)

Parameter optimization

Data smoothness processing

As the production of shale gas wells is affected by stimulation treatment, interference from adjacent wells, equipment maintenance, and other factors, there must be some volatility. However, the traditional GM(1, N) method has some limitations in dealing with volatile data series. The reason is that the original data did not meet the smoothness requirements of the prediction model (Kung and Yu 2008). Therefore, in order to predict shale gas well production more accurately, the screened raw data are pre-processed to make the processed data satisfy the smoothness requirement of the prediction model.

If the original data sequence that has been smoothed is defined to be \(X_{i} ^{\prime}\left( 0 \right)\), then:

$$X_{i}^{\prime } \left( 0 \right) = \left[ \begin{gathered} x_{1}^{\prime (0)} \left( 1 \right),x_{1}^{\prime (0)} \left( 2 \right), \ldots x_{1}^{\prime (0)} \left( n \right) \hfill \\ x_{2}^{\prime (0)} \left( 1 \right),x_{2}^{\prime (0)} \left( 2 \right), \ldots x_{2}^{\prime (0)} \left( n \right) \hfill \\ \ldots \hfill \\ x_{N}^{\prime (0)} \left( 1 \right),x_{N}^{\prime (0)} \left( 2 \right), \ldots x_{N}^{\prime (0)} \left( n \right) \hfill \\ \end{gathered} \right]$$
(12)

where

$$x_{i}^{\prime (0)} (j) = In \, x_{i}^{(0)} (j)\quad i = 1,2, \ldots ,N;\,j = 1,2, \ldots ,n.$$
(13)

The processed data then are used as the original modelling data for prediction, and the prediction results are restored exponentially after the prediction is finished:

$$\widehat{x}_{i}^{(0)} \left( k \right){ = }e^{{\widehat{x}_{i}^{^{\prime}(0)} \left( k \right)}}.$$
(14)

Background value optimization

The accuracy of GM(1, N) is directly related to its time response function Eq. (8). The parameters that determine the time response function are the developing coefficient \(a\) and the grey action quantity \(b\). However, the values of \(a\) and \(b\) are related directly to the background value. Therefore, the key to improving the accuracy of GM(1, N) is to construct better formulae for calculating the background value. It can also be seen from Eq. (5) that the background value is the average value of \(x_{1}^{\left( 1 \right)} \left( k \right)\) and \(x_{1}^{\left( 1 \right)} \left( {k - 1} \right)\) in Fig. 1. Apparently, the use of the two-point average formula to calculate the integral value of the nonlinear function will bring about great errors. The accuracy of G(1, n) can be improved by using a more reasonable numerical integration method to calculate background value (Shen et al. 2012).

Fig. 1
figure 1

Schematic map of GM(1, N) error

Full size image

In the present study, the background value optimization is proposed to improve the accuracy of G(1, n).

For the interval [− 1,1], the Gauss–Legendre quadrature formula is (Sidi 2009):

$$\int\limits_{{{ - }1}}^{1} {f\left( x \right)} dx{ = }\sum\limits_{k = 0}^{n} {A_{k} f\left( {x_{k} } \right)}.$$
(15)

The expression of the Nth Legendre polynomial in [− 1,1] is:

$$\begin{aligned} P_{n} \left( x \right) & = \frac{1}{{2^{n} n!}} \cdot \frac{{{\text{d}}^{n} }}{{{\text{d}}x^{n} }}\left[ {(x^{2} - 1)^{n} } \right] \\ & = \frac{1}{{2^{n} n!}}\left( {2n} \right)\left( {2n - 1} \right) \cdot \cdot \cdot \left( {n + 1} \right)x^{n} + a_{n - 1} x^{n - 1} + \cdot \cdot \cdot + a_{0}. \\ \end{aligned}$$
(16)

Nth Legendre polynomial is an orthogonal polynomial with the interval [− 1,1]. Therefore, the zero point of the Legendre polynomial is the Gauss point of Eq. (15) and \(x_{k} \, \left( {0,1, \ldots ,n} \right)\) is the zero point of the \(N{ + }1\) Legendre polynomial.

Let \(x = \frac{b - a}{2}t + \frac{b + a}{2}\), and transform interval [a,b] to [− 1,1]:

$$\int\limits_{a}^{b} {f\left( x \right)} dx{ = }\frac{b - a}{2}\int_{ - 1}^{1} {f\left( {\frac{b - a}{2}t + \frac{b + a}{2}} \right)dt}.$$
(17)

The Gauss–Legendre formula for N = 5 is used, so the new background value calculation method is:

$$\begin{aligned} z_{1}^{(1)} \left( k \right) & { = }0.1185x_{1}^{(1)} \left( {k + 0.0469} \right){ + }0.2393x_{1}^{(1)} \left( {k + 0.2307} \right) \\ \;\;\;\;{ + }0.2844x_{1}^{(1)} \left( {k + 0.5} \right){ + }0.2393x_{1}^{(1)} \left( {k + 0.7692} \right){ + }0.1185x_{1}^{(1)} \left( {k + 0.9531} \right). \\ \end{aligned}$$
(18)

The background value can be calculated more accurately by using Eq. (18) instead of Eq. (5). \(x_{1}^{(1)} \left( k \right)\) is the discrete data in a discrete sequence. The values of \(x_{1}^{(1)} \left( {k + 0.0469} \right)\), \(x_{1}^{(1)} \left( {k + 0.2307} \right)\), \(x_{1}^{(1)} \left( {k + 0.5} \right)\), \(x_{1}^{(1)} \left( {k + 0.7692} \right)\), and \(x_{1}^{(1)} \left( {k + 0.9531} \right)\) cannot be obtained accurately. To solve this problem, the expression \(x_{1}^{(1)} \left( k \right)\) is given by exponential function (Jiang et al. 2014; Ma et al. 2014):

$$x_{1}^{(1)} \left( k \right) = Be^{Ak}$$
(19)

where

$$\begin{gathered} A = {\text{In}}\left( {x_{1}^{(1)} \left( {k + 1} \right)} \right) - {\text{In}}\left( {x_{1}^{(1)} \left( k \right)} \right) \hfill \\ B = \frac{{x_{1}^{(1)} \left( k \right)}}{{e^{{{\text{In}}\frac{{x_{1}^{(1)} \left( {k + 1} \right)}}{{x_{1}^{(1)} \left( k \right)}}k}} }}. \hfill \\ \end{gathered}$$
(20)

The values of \(x_{1}^{(1)} \left( {k + 0.0469} \right)\), \(x_{1}^{(1)} \left( {k + 0.2307} \right)\), \(x_{1}^{(1)} \left( {k + 0.5} \right)\), \(x_{1}^{(1)} \left( {k + 0.7692} \right)\), and \(x_{1}^{(1)} \left( {k + 0.9531} \right)\) can be obtained accurately from Eqs. (19) and (20).

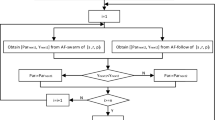
Solution process

For the present application, the solution process for the model can be summarized as follows:

  1. 1.

    Smooth the original data \(X_{i}^{(0)}\) logarithmically, and the processed data \(X_{i} ^{\prime}\left( 0 \right)\) are taken as the original modelling data sequence.

  2. 2.

    Accumulate the original modelling data sequence \(X_{i} ^{\prime}\left( 0 \right)\) once by Eq. (3) to generate the accumulated sequence \(X_{i}^{(1)}\).

  3. 3.

    Calculate the background value \(z_{1}^{(1)} \left( k \right)\) using Eq. (18), and the improved GM(1, N) model is established.

  4. 4.

    Obtain the value of \(B\) using the optimized background value \(z_{1}^{(1)} \left( k \right)\) according to the least-squares method Eq. (11), then the value of \(a\),\(b_{2}\),\(\ldots\),\(b_{n}\) is obtained from Eq. (10), and the value of \(\widehat{x}_{1}^{(1)} \left( {k + 1} \right)\) is obtained from Eq. (8).

  5. 5.

    Finally, the predicted value \(\widehat{x}_{1}^{(0)} \left( {k + 1} \right)\) of the feature series is obtained using Eqs. (9) and (14).

Results and discussion

The production data were obtained for Well W1 for 20 days (Table 1). Data from the first 16 days were used for model building, and data from the last 4 days were used to test the prediction results. In addition, the model was evaluated by comparison with results from the mean square error [MSE, Eq. (19)], mean relative percentage error [MRPE, Eq. (20)], relative mean squares [RMS, Eq. (21)], and the linear correlative coefficient [R, Eq. (22)].

$${\text{MSE } = \text{ }}\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {x_{i} - \widehat{{x_{i} }}} \right)}^{2}$$
(21)
$${\text{MRPE } = \text{ }}\frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{x_{i} - \widehat{{x_{i} }}}}{{x_{i} }}} \right|} \times 100\%$$
(22)
$${\text{RMS } = \text{ }}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {x_{i} - \widehat{{x_{i} }}} \right)}^{2} }$$
(23)
$$R{ = }\frac{{n\sum\limits_{i = 1}^{n} {\left( {x_{i} \widehat{{x_{i} }}} \right)} - \left( {\sum\limits_{i = 1}^{n} {x_{i} } } \right)\left( {\sum\limits_{i = 1}^{n} {\widehat{{x_{i} }}} } \right)}}{{\sqrt {\left[ {n\sum\limits_{i = 1}^{n} {\left( {x_{i} } \right)^{2} - \left( {\sum\limits_{i = 1}^{n} {x_{i} } } \right)^{2} } } \right]\left[ {n\sum\limits_{i = 1}^{n} {\left( {\widehat{{x_{i} }}} \right)^{2} - \left( {\sum\limits_{i = 1}^{n} {\widehat{{x_{i} }}} } \right)^{2} } } \right]} }}.$$
(24)
Table 1 Daily production rate of well W1
Full size table

The model established in the present study was compared with MEP (Ma and Liu 2016; Oltean and Dumitrescu 2002), conventional GM(1, N) (Ma et al. 2014), and traditional GM(1, 1) (Ikram et al. 2019; Julong 1982; Liu and Deng 1996). The production rate is simulated using the data shown in Table 1. Figure 2 shows the results as simulated by the different methods; Table 2 shows the evaluation indices results.

Fig. 2
figure 2

The simulated results with different models

Full size image
Table 2 Evaluation indices results
Full size table

As shown in Fig. 2, GM(1, 1) can be applied only to progressive or decreasing data prediction; it cannot be applied for the prediction of fluctuating series. Conventional GM(1, N), MEP, and the improved GM(1, N) model can be used to predict fluctuating production data, which can reflect the direction and amplitude of fluctuation in the production data and has a good prediction capability. As shown in Table 2, the evaluation results indicate that the model established in the present study had the smallest covariance and higher prediction accuracy. The linear correlation coefficient R shows that the calculated results of GM(1, 1) were almost fixed, leading to an R-value for its predicted results that was very close to zero, and the prediction effect was the worst. The trend for the MEP prediction results was contrary to the trend of the actual production data. However, the improved GM(1, N) model had a slight advantage over the conventional GM(1, N) on data relevance.

As the improved GM(1, N) model mimics the fluctuations of the original data by processing a series of data related to the simulated data, it reflects the trends of the original data under the influence of relevant factors and can more accurately predict the fluctuation amplitude and direction of the original data. Figure 3 shows the trend of the predicted results of the relevant parameters and the relative errors between the predicted values and the original values. The improved GM(1, N) model first predicts the casing pressure at well start-up through GM(1, 1). Then, based on the trend of casing pressure at well start-up, it predicts the tubing pressure at well start-up. Next, based on the casing pressure and the tubing pressure at well start-up, it predicts the tubing pressure at shut-in and so on and finally estimates the overall shale gas production rate with fluctuating characteristics. From the variation trend of Fig. 3a, e and the relative error shown in Fig. 3f, the prediction accuracy increases gradually and the relative error decreases gradually according to the sequence of casing pressure at well start-up, tubing pressure at well start-up, tubing pressure at shut-in, water production, and shale gas production. Therefore, such a step-by-step prediction method can effectively improve the accuracy of production rate/volume predictions and accurately reflects the fluctuation characteristics of shale gas production.

Fig. 3
figure 3

Original data, simulated data, and the relative error between the simulated data and the original data

Full size image

Conclusions

The present investigation focused upon identification of the causes of the error of the conventional GM(1, N) shale gas production estimation method. Taking the production of shale gas wells as the research object, an improved GM(1, N) model-based shale gas well productivity prediction model has been proposed. After verifying the accuracy of the improved model, the following conclusions were reached:

  1. 1.

    The improved G(1, n) model mimics the fluctuation of the original data by the processing of a series of data related to the predicted data. In consequence, it can better reflect the trends exhibited in the original data under the influence of relevant factors pertaining to the reservoir and more accurately predicts the fluctuation amplitude and direction from the original data.

  2. 2.

    For the data in the present example, the improved GM(1, N) method had a slight advantage over the conventional GM(1, N) method on data relevance and had significant advantages over the GM(1, 1) method and the MEP method. Additionally, the improved GM(1, N) method had the smallest covariance and exhibited greater predictive accuracy.

  3. 3.

    Prediction accuracy gradually increased, and the relative error gradually decreased from bottom data (e.g. casing pressure at well start-up, etc.) to top data (shale gas production volume/rate). A step-by-step prediction method such as this can improve prediction accuracy effectively and can reflect accurately the fluctuation characteristics of shale gas and shale gas production.