Thermal maturity and TOC prediction using machine learning techniques: case study from the Cretaceous–Paleocene source rock, Taranaki Basin, New Zealand

Abstract

Thermal maturity, organic richness and kerogen typing are very important parameters to be evaluated for source rock characterization. Due to the difficulties of high cost geochemical analyses and the unavailability of rock samples, it was necessary to examine and test many different method and techniques to help in the prediction of TOC values as well as other maturity indicators in case of missing or absence of geochemical data. Integrated study of machine learning techniques and well-log data has been applied on Cretaceous–Paleocene formations in the Taranaki Basin, New Zealand. A novel approach of maturity prediction using T_max and vitrinite reflectance (VR%) is the first and preliminary objective of this research. Moreover, the organic richness or the total organic carbon (TOC) content has been predicted as well. Geochemical and well-log data collected from the Cretaceous Rakopi and North Cape formations and Paleocene Mangahewa Formation have been processed and prepared to apply the machine learning techniques. Five machine learning techniques, namely Bayesian regularization for feed-forward neural networks (BRNNs), random forest (RF), support vector machine (SVM) for regression, linear regression (LR) and Gaussian process regression (GPR), were employed for prediction of TOC, T_max and VR, and their results have been compared. For TOC prediction, the best model achieved the coefficient of determination (R²) value of 0.964 using RF model. For T_max prediction, BRNN with one hidden layer achieved the R² value of 0.828. BRNN with two hidden layers produced the best model for VR prediction achieving R² = 0.636. A comparison of five ML techniques showed that all of these techniques performed exceedingly well for TOC prediction with a value of R² > 0.96. In contrast, BRNN with one hidden layer was the only ML technique able to achieve R² > 0.8 for T_max and BRNN with two hidden layers was the only ML technique able to achieve R² > 0.6 for VR prediction. Therefore, this research provides a strong empirical evidence that ML techniques can capture the nonlinear relationship between the well-log data and TOC as well as the maturity indicators which may not be fully understood by existing linear models.

Introduction

Conventional well-logging data have been used in the analyses of source rocks, particularly in case if geochemical data are missing or absent. Laboratory work and experts required to generate geochemical data are expensive and take time. Rock samples required for analyses are not easily available. Thus, it becomes necessary to examine and test many different method and techniques to help in the prediction of TOC values as well as other maturity indicators in case of missing or absence of geochemical data. Their application can be done in two ways: via 1) mathematical models and/or 2) data mining framework or machine learning intelligent systems. Both techniques have proven to provide accuracy and hence can become a reliable alternative solution in total organic carbon (TOC) content quantification (Liu et al. 2012; Jumat et al. 2017; Bolandi et al. 2015, 2017; Shi et al. 2016; Shalaby et al. 2019a). Mathematical models developed by Passey et al. (1990), Zhao et al. (2016) and many others have been used to not only evaluate the quantity of carbon, but also identify and discriminate producible source zones within a well-cored interval or formation. Jumat et al. (2017) utilized the use of conventional well-logging data via mathematical models, to evaluate the source rock potential of the major source rocks of the Taranaki Basin using eight selected wells distributed across the basin. Comparisons between their results and the measured core geochemical data have proven that the models can be applied with great confidence in the area if geochemical data are not available. Shalaby et al. (2019a) published the integrated study using well-log data in combination with machine learning techniques for the prediction of organic matter richness in Jurassic source rock in Shams Field NW Desert, Egypt. It has been concluded that both machine learning and well-log data can predict the TOC values with very high accuracy and have good correlation with the measured TOC values from the geochemistry dataset.

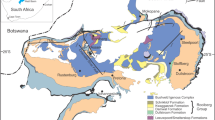
The study area of Taranaki Basin covers a total area of 100,000 km² and is located predominantly offshore on the west coast of the North Island between latitudes 38°00′ 41° 00′ S and longitudes 172°00′–175° 00′ E (Fig. 1). Ever since its maiden discovery in 1959, Taranaki Basin has remained as the overwhelmingly principal producer for petroleum in New Zealand, with over 1.8 billion barrels of BOE discovered (Webster et al. 2011). The basin contains all 20 of New Zealand’s presently producing fields, with over 400 wells drilled (New Zealand Ministry of Business 2014). Thus, studies pertaining to the basin, including its source rocks, are of great significance. In Taranaki Basin, the petroleum source originated from the deeply buried hydrogen-rich coals and terrigenous carbonaceous mudstones of the upper Cretaceous Pakawau Group and the Paleogene Kapuni Group (Johnston et al. 1989; King and Thrasher 1996). The Rakopi and North Cape formations from the Pakawau Group and the Mangahewa Formation from the Kapuni Group have been used to represent the source rocks in the study area. The great hydrocarbon potential of the source rocks from these three formations has been documented in more recent studies by Qadri et al. (2016) and Jumat et al. (2018). Many research works have been conducted in Taranaki Basin and Great South Basin in New Zealand, as well as some others all over the world to study the source rock characteristics, its thermal maturity and hydrocarbon generation modeling. Notable studies include Kalaitzidis et al. (2010), Kara-Gulbay et al. (2010), Shalaby et al. (2011, 2012a, b, c, 2019b), Hosseiny et al. (2016), Jumat et al. (2018) and Osli et al. (2018, 2019).

Fig. 1

Map of study area and selected wells (Compiled from Jumat et al. 2017)

The main objective of this research is to use the data mining framework or machine learning techniques to predict source rock characteristics in terms of TOC quantity and quality. Although mathematical models used by Jumat et al. (2017) have proven to be applicable in the study area, there is no similar guarantee that the machine learning method will produce the same favorable outcome. Additionally, while many machine learning techniques have been applied for TOC prediction in source rock characterization (Bolandi et al. 2015, 2017; Tan et al. 2015; Yu et al. 2017), only a few studies were found to have applied it for source rock maturity (Hussein and Abdula 2018). Therefore, this study aims to use the machine learning techniques to evaluate the accuracy in the prediction of source rock thermal maturity on the basis of maturity parameters T_max and %VR, in addition to predicting organic matter richness represented by TOC. Therefore, this study will, thus, prove to be beneficial in the current array of source rock studies not only limited to Taranaki Basin and can be used as a reference for other future studies.

Geological setting

The geological evolution of Taranaki Basin has been studied by numerous researchers, most notably by Thrasher (1992), King and Thrasher (1996), Palmer and Geoff (1988), Palmer (1985), and Pilaar and Wakefield (1978). The general consensus describes the formation of Taranaki Basin as being initiated when Australia and Zealandia split, following the breakup of the ancient supercontinent Gondwana. Taranaki Basin originated as one of the numerous extensional basins on the New Zealand subcontinent created alongside the subsequent formation of the Tasman Sea, aptly named the Taranaki Rift. This rift would later develop into the Taranaki Basin during the Late Cretaceous.

The Taranaki Basin was characterized by failed rift, subsidence and marine transgression in the Late Cretaceous, and intraplate to back-arc subsidence during the Neogene period (New Zealand Ministry of Business 2014). Due to its history and geographical extent, the basin has complex geological configurations, but the basin is generally classified into two structural blocks: (1) the Western Stable Platform and (2) the Eastern Mobile Belt (Fig. 1). The Western Stable Platform experienced extension during the late Cretaceous to Eocene but has remained relatively stable throughout the rest of the Tertiary (Pilaar and Wakefield 1978). The Eastern Mobile Belt, on the other hand, contains multiple extensional and compressional features that are still active to the present day.

Taranaki Basin is made up of terrigenous and marine sedimentary and volcanic rocks from the Cretaceous to Cenozoic age (Fig. 2). Its stratigraphy has been classified into four mega-sequences (King and Thrasher 1996):

Fig. 2

Simplified lithostratigraphic succession of the Taranaki Basin (Compiled from Jumat et al. 2017)

• a) Upper Cretaceous syn-rift sequence (Pakawau Group)

• b) Paleocene–Eocene late-rift and post-rift transgressive sequence (Kapuni and Moa groups)

• c) Oligocene–Miocene foredeep and distal sediment starved shelf and slope sequence (Ngatoro Group) and Miocene regressive sequence (Wai-iti Group)

• d) Plio-Pleistocene regressive sequence (Rotokare Group)

As previously mentioned, the source rocks of Taranaki Basin consist of hydrogen-rich coals and terrigenous carbonaceous mudstones of the upper Cretaceous Pakawau Group and the Paleogene Kapuni Group (Johnston et al. 1989; King and Thrasher 1996). The source rocks of the Pakawau Group are from the Rakopi and North Cape formations. Rakopi Formation comprises almost entirely of terrestrial coal measures, predominantly sandstone, cyclically interbedded with carbonaceous siltstone and mudstone, thin coal seams and rare conglomerate. The North Cape Formation is primarily distinguished from the Rakopi Formation by its marine depositional influence and consists of transgressive sandstones, with siltstone, mudstone and coal lithologies. The Kapuni Group source rocks studied in this paper are represented by the Mangahewa Formation which predominantly consists of sandstone, siltstone, mudstone and bituminous coal (Palmer 1985).

Materials and methods

Complete dataset and rock samples have been provided by the Ministry of Business, Innovation and Employment (MBIE) of New Zealand. Re-evaluation and publication of the dataset have been approved and authorized by the Ministry of Business, Innovation and Employment (MBIE) of New Zealand.

Eight wells scattered across the basin (Fig. 1) have been selected to examine the source rock characteristics: Tane-1 and Cape Farewell-1 wells for Rakopi Formation, Fresne-1, North Tasman-1 and Tane-1 wells for North Cape Formation, and Cardiff-1, Inglewood-1, Maui-3 and Maui-4 wells for Mangahewa Formation. Well names, formation thickness and drilled depths in all studied wells are presented in Table 1. The locations of these wells are mapped in Fig. 1.

Table 1 Well-log data information in this study

To ensure the applicability of the intelligent systems in the prediction of source rock characteristics, the results from this study are compared to the core geochemical data. The core data include the total organic carbon (TOC) content, Rock–Eval pyrolysis yields (S₁, S₂ and T_max), vitrinite reflectance VR% and well-logging data from the aforementioned selected wells. Machine learning utilizes these data to produce a holistic source rock characterization, which is not limited to the organic matter quantity but also its maturity.

Relationships between TOC content and responses of well-logging tools have been studied by several notable scholars, such as Carpentier et al. (1989), Fertle (1988), Fertle and Rieke (1980), Herron (1988), Meyer and Nederlof (1984), Passey et al. (1990) and Schmocker (1979, 1981), Schmocker and Hester (1983) and Zhao et al. (2016). Well-logging data, accordingly, have been taken as the input parameters for evaluating TOC content values for the rock samples selected in this study. The well-log data used include the conventional well-log tools of Gamma ray (GR), sonic (DTC), neutron (NPHI), density (RHOB) and true resistivity (RT). The typical well-log responses to the presence of source rocks can be described as follows:

• 1. Gamma ray log: It measures the radioactivity of a formation (Serra 1984). Organic matter is associated with Uranium content, and hence, its presence leads to an increase in GR readings.

• 2. True resistivity log: It measures the conductivity of a fluid within a formation. In mature source rocks, the resistivity increases due to the presence of generated hydrocarbons (Passey et al. 1990). The RT readings in mature source rocks increase significantly by a factor of 10 or more (Meyer and Nederlof 1984).

• 3. Sonic log: It measures the travel time of an elastic wave through a formation and inversely can be used to derive its velocity through the same formation. Immature source rocks travel faster than mature source rocks.

• 4. Density log: It measures the bulk density of a formation, which is influenced by fluids and matrix constituent mineral density (Asquith 1982; Schlumberger 1989). As organic matter has a low density (~ 1 g/cm³), the bulk density of source rocks is typically low.

• 5. Neutron log: It measures the response of hydrogen atoms concentration in a formation (Serra 1984). The hydrogen atoms and porosity within a formation have a direct relationship with the organic matter content. This means that the values for neutron porosity increase where there are high H Index, organic-rich intervals.

In terms of source rock maturity, the Rock–Eval pyrolysis yield T_max and vitrinite reflectance (%VR) are the two indicators used in this research to assess whether the source rocks studied have attained enough maturity. T_max is the temperature at which the maximum rate of hydrocarbon generation occurs in a kerogen sample during pyrolysis analysis. %VR is a technique is used in organic petrography, and it measures the amount of light reflected by vitrinite present in the rock’s organic component. Following classification made by Peters and Cassa (1994), the onset of maturity or “oil window” for the studied sock rocks is at 430 °C T_max and 0.5%VR.

Jumat et al. (2017) applied three renowned mathematical models namely Schmocker and Hester (1983), Passey et al. (1990) and Zhao et al. (2016) for organic richness evaluation on the same eight wells from Taranaki Basin as studied in this paper. The models are applied on the source rock intervals, and the results were calibrated with geochemical TOC values. An exemplary figure is included in Fig. 3 to show that good correlation was observed between the TOC values from the models and geochemical set. Therefore, and for better accuracy, this paper will pay more intention to focus on the prediction of maturity indicators T_max and % VR to explore how much guarantee that ML techniques can be used in the absence of geochemical dataset.

Fig. 3

Correlation of TOC results between well-log models and geochemical dataset for the source interval in selected well (Taken from Jumat et al. 2017)

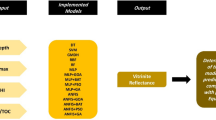
Figure 4 shows the work flow of the data analysis performed in this study, while all steps will be explained as follows:

Fig. 4

Steps for performing the predictive data analysis using machine learning techniques

Pre-processing of datasets

The collected data were divided into four data sets. For TOC prediction, the studied dataset consisted of 68 samples: 15 from Mangahewa, 12 from North Cape and 38 from Rakopi formations. Conventional well-log data (GR, RHOB, DTC, and RT) as well as lithology have been used to perform the TOC prediction. Parameter NPHI was, however, excluded due to high unavailability of complete data. For T_max prediction, two datasets were experimented: one containing instances with coal lithology (86 samples) and one without coal lithology (52 samples). The well-logging and geochemical parameters (depth, GR, RHOB, DTC and RT) were used for the prediction of T_max. For the prediction of vitrinite reflectance %VR, same input parameters were used. However, actual VR values are not available for samples with coal lithology, and thus, only samples with mudstone and shaly coal lithology are used (52 samples). Samples of well-log attributes with the same depth to the nearest meter were averaged, and then the averaged well-log data were matched with the corresponding geochemical data of the same depth.

For the predictive modeling of each parameter TOC, T_max and VR, the attributes selected for training were based on common domain knowledge that these are highly relevant attributes associated with parameters of interest to be predicted.

Table 2 shows no correlation between well-log parameters GR, RHOB, DTC, RT and geochemical parameter TOC. Table 3 shows there is weak correlation (less than 0.7) between T_max and other well-log parameters. Weak correlation is also found between VR and other well-log parameters in Table 4. As the correlations found are weak, we can proceed to apply machine learning to solve our research problem.

Table 2 Correlation between well-log parameters and TOC

Table 3 Correlation between well-log parameters and T_max

Table 4 Correlation between well-log parameters and VR

Preparation of data sets for training/testing

The well-logging data, together with relevant parameters from geochemical analysis, were scaled and centered. All data were numeric except for lithology parameter which had nominal values. To perform regression or numeric prediction with nominal data, the lithology values were represented using dummy variables (one hot encoding). The data sets were split into train and test subgroups, containing 75% and 25% of the samples, respectively. Repeated tenfold cross-validation was used during training, and the best model (with the lowest root-mean-squared error) was chosen (after performing parameter tuning) to be evaluated on the testing set. The experiment was repeated 50 times to study the stability of the algorithms’ average performance, based on the coefficient of determination (R²).

TOC, T_max and %VR prediction using machine learning techniques

Initially, various machine learning techniques were applied on all data sets. After preliminary experimentation, five best machine learning algorithms from various categories/classes were chosen, applied and compared to predict the TOC, T_max and %VR values for the selected formations in the Taranaki Basin. A complete set of well-log data collected from Mangahewa, North Cape and Rakopi formations in the Taranaki basin, New Zealand, was used for this purpose. The algorithms Bayesian regularization for feed-forward neural networks (BRNN) and random forest (RF) were explored, and the results were compared with other algorithms such as support vector machine (SVM) for regression with linear kernel, linear regression (LR) and Gaussian process with radial basis function kernel (GPR). The BRNN and RF algorithms which generated the best results are explained in greater detail, while the others are briefly described below. They are all implemented using MATLAB 2018. Out of these five algorithms, the results with the best performing models are presented in full detail.

Bayesian regularization for feed-forward neural networks (BRNN)

Artificial neural network is widely used in TOC prediction (Bolandi et al. 2015). To avoid the overfitting problem with artificial neural networks (Schittenkopfab et al. 1997) and simplifying the parameter setting, we explored a different type of neural networks, Bayesian regularized neural networks (BRNN), which has never been used before for this purpose.

Pérez-Rodríguez et al. (2013) introduced a single hidden layer feed-forward neural network model for approximating nonlinear function. The model focused on both additive and dominance effects using empirical Bayes approach to calculate all parameter estimates and penalizes network parameters which are nonzero. The neural network is made up of network connections of nodes for learning the mapping between input patterns and output nodes. It contains three layers: the input layer, hidden layer and output layer. The mapping is learned via optimizing the weights of connections by adjusting them at each iteration. The algorithm proposed by Pérez-Rodríguez et al. (2013) is briefly described as follows:

To fit a NN model that includes additive and dominance effects jointly described below, the algorithm below is followed:

$$y_{i} = \mu + \mathop \sum \limits_{k = 1}^{{S_{a} }} w_{k}^{a} g \left( {b_{k}^{a} + \mathop \sum \limits_{j = 1}^{p} x_{ij} \beta_{j}^{a\left[ k \right]} } \right) + \mathop \sum \limits_{k = 1}^{{S_{d} }} w_{k}^{d} g \left( {b_{k}^{d} + \mathop \sum \limits_{j = 1}^{p} \beta_{j}^{d\left[ k \right]} } \right) + \varepsilon_{i }$$

(1)

where $(w_{1} , \ldots ,w_{s} )$ are network weights; $(b_{1} , \ldots ,b_{s} )$ are biases; $(\beta_{1}^{\left[ 1 \right]} , \ldots ,\beta_{p}^{\left[ 1 \right]} ; \ldots ; \beta_{1}^{\left[ s \right]} , \ldots , \beta_{p}^{\left[ s \right]} )^{{\prime }}$ are connection strengths where $\beta_{j}^{\left[ k \right]}$ denotes a parameter for input j in neuron $k = 1, \ldots ,s,$ and $g_{k} ( \cdot )$ is the activation function, which maps inputs to bounded (−1, 1). $s_{a}$ and $s_{d}$ are numbers of neurons for the additive and dominance components, respectively, in the hidden layers. Parameter $\mu$ is eliminated by centering observations for simplicity.

Step 1: Initialize $\beta ,\alpha ,\delta$ and the weights using the Nguyen and Widrow (1990) algorithm.

Step 2: Take one step of the Levenberg–Marquardt algorithm to minimize the objective

$$Q\left( \varphi \right) = \beta \mathop \sum \limits_{i = 1}^{n} e_{i}^{2} + \alpha \theta_{a}^{'} \theta_{a} - \delta \theta_{d}^{'} \theta_{d}$$

(2)

function $Q\left( \varphi \right)$ given in (2).

Where $\varphi$ denotes a vector of dimension $t \times 1$ including all connection strengths and coefficients for additive and dominance effects, including weights and biases, n is the number of observations, e_i is the prediction error, $\theta_{a}$ denotes the vector of dimension $m \times 1$ with strengths for additive effects and $\theta_{d}$ denotes the vector of dimension $q \times 1$ with strengths for dominance effects. Note $m + q \cdot \beta = \frac{1}{{2\sigma_{e}^{2} }}$, $\alpha = \frac{1}{{2\sigma_{a}^{2} }}$ and $\delta = \frac{1}{{2\sigma_{d}^{2} }}$ where $\sigma_{e}^{2}$ is the residual variance, $\sigma_{a}^{2}$ and $\sigma_{d}^{2}$ are variances of connection strengths and weights for additive and dominance effects, respectively.

Step 3: Update $\beta ,\alpha ,\delta$ by maximizing (3) using the Nelder and Mead (1965) algorithm.

$$\begin{aligned} & G\left( {\beta , \alpha , \delta , \varPsi = \varPsi^{\text{map}} } \right) = \log p \left( {y|\varPsi , \sigma_{e}^{2} } \right) \\ & \quad \approx c + \frac{n}{2}\log \beta + \frac{m}{2}\log \alpha + \frac{q}{2}\log \delta - \frac{1}{2}\log |\varSigma |_{{\varphi = \varphi^{\text{map}} }} - Q\left( \varphi \right)|_{{\varphi = \varphi^{\text{map}} }} \\ \end{aligned}$$

(3)

where c is a constant, ${\varvec{\Psi}} = \left( {\sigma_{a}^{2} , \sigma_{d}^{2} } \right)'$, $\varSigma = \nabla^{2} Q\left( \varphi \right) = \beta \nabla^{2} \mathop \sum \nolimits_{i = 1}^{n} e_{i}^{2} + \alpha \nabla^{2} \theta_{a}^{{\prime }} \theta_{a} - \delta \nabla^{2} \theta_{d}^{{\prime }} \theta_{d}$ and $\varSigma$ is the Hessian matrix.

Step 4: Iterate Steps 2 and 3 until convergence.

The full derivation for BRNN can be found in Pérez-Rodríguez et al. (2013).

Random forest (RF)

Random forest (Breiman 2001) is an ensemble technique based on building many decision trees to determine the classes or make prediction of each of the trees, for regression, classification and other learning tasks. Random trees with different attributes at the splits are built using randomly generated training sets (bagging) and their learning performance evaluated to find the best performing tree. Using bagging helps alleviate problems of overfitting and reduce variance. This makes it a suitable algorithm for this study, seeing overfitting as occurred in most of the neural network-based approaches.

When building a decision tree, the selection of attributes at each step to best split observations can be based on a chosen metric such as the Gini impurity. The Gini impurity measures the likelihood of a wrong classification of a new observation of a feature, if the observation was classified randomly based on class labels distribution from the dataset. It is calculated as follows:

$$G = \mathop \sum \limits_{i = 1}^{C} p\left( i \right)*\left( {1 - p\left( i \right)} \right)$$

(4)

where C is the number of classes and p(i) is the probability of randomly picking an observation of class i.

The Gini impurity before and after the split is calculated, and the best split is chosen by the maximum Gini gain, obtained from a weighted subtraction from the impurity before splitting.

To the best of our knowledge, random forests have so far not been applied on well-logging data for TOC prediction. Motivated by its good performance (Breiman 2001) and application in existing studies such as for soil organic carbon (Zhang et al. 2017; Were et al. 2015), this algorithm has been explored.

Support vector machine for regression (SVM)

Tan et al. (2015) has applied SVM, experimenting with Epsilon-SVM, Nu-SVM and SVM with Sequential Minimal Optimization (SMOSVM) as novel approaches for TOC prediction. The motivation for applying SVM was its ability to solve nonlinear problems in small sample with high dimensions. One main challenge of SVR is the setting of parameters: penalty coefficient, the Gaussian spread or gamma and insensitive loss factor (ε), all of which greatly affect prediction performance.

Linear regression (LR)

Linear regression is the simplest technique for performing numeric prediction, such as to predict TOC, VR or T_max values by finding the relationship between a dependent variable and one or more independent variables. The exploration using LR was motivated by a study using linear regression techniques where it was found to perform well in predicting soil organic carbon (Zhang et al. 2017). Hussein and Abdula 2018 had applied multiple linear regression for %VR estimation using well logs.

Gaussian process with radial basis function kernel (GPR)

Gaussian process is a nonparametric regression technique which uses a Bayesian approach to capture different relations between inputs and outputs (Schulz et al. 2018). Yu et al. (2017) successfully applied Gaussian process regression for TOC estimation using well logs in shale gas reservoirs.

Performance evaluation metrics

The following three performance evaluation metrics were computed for each model and the results were compared.

• I. Root-mean-square error (RMSE): It is the root of average squared difference between actual outputs (Y_i) and the predicted output $(\hat{Y}_{i} )$. The model with lower value of RMSE is considered better as compared to a model having higher value of it.

• II. Coefficient of Determination (R²): It is the proportion of variability in output variable explained by the machine learning model. The value of R² is reported between 0 and 1, and a model with higher value of coefficient of determination is considered more accurate.

• III. Mean absolute error (MAE): It is the average of the absolute difference between actual outputs (Y_i) and the predicted output $(\hat{Y}_{i} )$. This metric avoids the unnecessary effect of outliers which may be present in the first two evaluation measures.

Predictor importance estimation

• Predictor importance estimation has been performed using the input perturbation-based neural network sensitivity analysis. The sensitivity analysis finds that varying certain input parameters from their minimum to their maximum will have a greater/less effect on the resulting network (Montaño and Palmer 2003; Gedeon 1997). Using this approach, the relative degree of influence of the input parameters toward the prediction of the TOC, T_max and VR parameters was determined based on the best trained model.

Results and discussion

Different machine learning techniques have been applied to predict source rock quantity represented by TOC. Moreover, the maturity parameters represented by the maximum pyrolysis temperature T_max and vitrinite reflectance have also been examined. The best models found for TOC, T_max and %VR prediction are presented in Table 5.

Table 5 Best models and performance metrics values

TOC prediction

Comparison of ML techniques performance

The training and testing results of selected ML techniques for TOC prediction are shown in Fig. 5a, b, respectively. In Fig. 5a, RF is observed to produce the best results in terms of accuracy (R² value), with the highest testing accuracy of 0.964. Its MAE value of 3.33 is lower than SVM and GPR. Performing competitively is BRNN which produced testing accuracy of 0.963 and MAE values of 3.25. SVM, GPR and linear regression (LR) demonstrated good performance with testing accuracy of near 0.950 and above and MAE values between 3.31 and 3.35. In general, the five ML techniques performed exceedingly well with near or above 0.950 testing accuracy (R²) for TOC prediction. No overfitting is observed in the prediction as shown in both graphs (Fig. 5a, b) of testing and testing accuracies.

Fig. 5

Results for TOC prediction a testing, b Training

The plots of actual and predicted TOC using the selected ML as found as follows: RF in Fig. 6a, BRNN in Fig. 6b, LR in Fig. 6c, SVM (Linear) in Fig. 6d and GPR in Fig. 6e. Most of the predicted results generated from these techniques were found to be close to the actual results except for a few TOC values predicted by BRNN, LR, SVM and GPR. Interestingly, most TOC predicted values tend to plateau in the LR, SVM and GPR models.

Fig. 6

Plot of actual TOC versus predicted TOC using a RF, b BRNN, c LR, d SVM and e GPR

The inclusion of lithology in our modeling has separated the TOC into three intervals, each of which represent samples from the respective lithology, thus contributed greatly to TOC prediction, as shown in the testing results of RF’s predicted TOC plotted with actual TOC in Fig. 6a. This trend is reflected in the testing results of BRNN, LR, SVM (linear) and GPR in Fig. 6b–e, respectively.

Random forest in TOC prediction

The best results of TOC prediction are found using the random forest algorithm. Figure 7a shows that the results start to converge when the number of trees used are more than 25. The fluctuations in R² across the number of trees are below 0.005, which can be considered negligible, thus demonstrating the stability of the results across the number of trees.

Fig. 7

a RF performance in terms of accuracy and RMSE versus no. of trees, b objective function model for RF

The optimized hyperparameters are minLS = 1 and numPTS = 7, where the estimated objective function values over various combinations of minLS and numPTS are displayed in Fig. 7b. numPTS denotes the number of predictors to consider at each node when growing the trees, while minLS denotes the depth of the tree.

Figure 8a shows the minimum objective value against the number of function evaluations where the algorithm is able to find good models using as little as 11 function evaluations, demonstrating the computational requirements of RF for TOC prediction. The minimum value of the objective function was found around 0.0064 as shown in Fig. 8a.

Fig. 8

a Min objective versus number of function evaluations of RF in TOC prediction, b predictors' importance estimates using RF in TOC prediction

Generally, from the lithological point of view, the organic matter tends to be concentrated in sediments with specific sedimentological and depositional history. Coal and coaly sediments are characterized by higher TOC content which may reach to more than 70% in many cases. On the other hand, clastic sediments like shale, shaly materials and mudstones normally have lower TOC content if compared with coaly sediments (up to 30–40%).

Therefore, it has been observed that for RF, the lithology types have the greatest importance in TOC prediction due to the impacts of lithology in the total organic matter content (TOC). Increasing of TOC values particularly in coal with the highest TOC values above 70% has showed the higher degree of predictors' importance (Fig. 8b). The next highest predictor estimates have been followed by other lithology materials like mudstones and shaly coal with lower TOC values between 15 to 45%. The prediction of the TOC content has been affected by other well-log data such as Gamma Ray and resistivity logs (Fig. 8b). This is consistent with Fig. 6a where coal has highest TOC interval values followed by shaly coal and mudstones. RF regarded DTC to have least importance with a negative predictor importance score for TOC prediction.

BRNN in TOC prediction

The performance of BRNN was quite similar to the random forest algorithm in predicting the TOC values. The BRNN algorithm starts to converge during training at 5 neurons (Fig. 9). Note that while the fluctuations look drastic on the plot, these fluctuations are in fact small with highest difference values of about 0.005, demonstrating the stability of BRNN results.

Fig. 9

BRNN performance in terms of accuracy and RMSE versus no. of neurons in TOC prediction

This study shows that RF-based ML model is quite suitable for the prediction of TOC as compared to previous studies where mostly SVM and ANN regression models have been applied for prediction of TOC (Ge et al. 2015; Mahmoud et al. 2017; Negara et al. 2016; Bolandi et al. 2017; Elkatatny 2018). The results of RF-based model are well comparable with the previous studies having high R² values and low values of training and testing MAE values (Ge et al. 2015; Mahmoud et al. 2017; Negara et al. 2016; Bolandi et al. 2017). Moreover, the reported importance of different predictors for developing the model also provides an insight about nature of data and dependency of TOC on different factors for this data set.

T_max prediction

Comparison of ML techniques performance

The performance of selected ML algorithms was found to be poor for predicting the values of T_max except for BRNN with one hidden layer, producing 0.834 and 0.828 R² values for training and testing, respectively (Table 5). Figure 10a and b shows that the best testing and training results, respectively, in terms of accuracies (R²) and MAE, are produced by BRNN with two hidden layer, achieving values of above 0.8 accuracy and less than 1.5 MAE. Apart from one-hidden-layer BRNN, all other ML techniques achieved R² values of less than 0.7. The training results presented in Fig. 10b showed no evidence of over fitting for BRNN.

Fig. 10

Results for T_max prediction a testing, b training

BRNN in T_max prediction

Using one hidden layer in BRNN, coefficients of determination (R²) of above 0.8 can be achieved in T_max prediction with 19 neurons in the one hidden layer, as shown in Fig. 11a. Those with first and second layers with less than 3 and 14 neurons, respectively, were found to have 0.6 or less testing accuracy. These results were not found to be overfitting as training accuracy was also found to achieve above 0.8 with 19 neurons. The best testing results were found with 5 and 19 neurons for first and second hidden layers, respectively. Figure 11b shows how close BRNN predicted T_max values are to the actual values, demonstrating good performance from BRNN. The importance of depth in the maturity of source rock is well known due to increasing of temperature and pressure. Therefore, it has been noticed that the depth factor is the top most important predictor for T_max prediction (Fig. 11c). Moreover, resistivity and density logs are other important well-log parameters to be involved in the T_max prediction (Fig. 11c). This is because the maturity of source rock and the expulsion of hydrocarbon have great impact on the resistivity and other logs measured in the borehole.

Fig. 11

a BRNN performance in terms of accuracy and RMSE versus no. of neurons in T_max prediction, b plot of actual T_max versus BRNN predicted T_max, c Predictors’ importance estimates using BRNN in T_max prediction

%VR prediction

Comparison of ML techniques performance

BRNN with two hidden layers produced the best result as compared to the other five ML techniques (Fig. 12a). Achieving testing accuracy (R²) and MAE values of 0.636 and 0.033, respectively, has been observed (Table 5), with no evidence of overfitting in the training accuracy (Table 5, Fig. 12b). The other ML techniques produced results with less than 0.5 R² values.

Fig. 12

Testing results for VR prediction a testing, b training

BRNN in VR prediction

BRNN with 2 to 5 neurons in the first hidden layer and with 5 or 15 to 20 neurons in the second hidden layer can achieve a testing accuracy of above 0.6 (Fig. 13a). It has been observed that slightly better accuracy during training in the region of low neurons – 2 to 5 neurons in both layers (Fig. 13b), which demonstrates the prediction is not overfitting in the chosen model. The best testing results were found with 4 and 20 neurons for first and second hidden layers, respectively. The comparison between the actual VR and predicted VR observations is found to be close to actual ones (Fig. 14a). These results demonstrate that a two-layer BRNN produced a good predictive model for VR prediction. The vitrinite reflectance, VR, as maturity indicator has a good relationship with depth increment. For great depth zones, normally VR values reflect more mature and then the measured resistivity logs are also increased. Figure 14b is in good agreement that depth and resistivity are the most important predictors for VR prediction, which are followed by RHOB and GR.

Fig. 13

BRNN performance in terms of coefficient of determination (R²) versus no. of neurons in each hidden layer in VR prediction a testing, b training

Fig. 14

a Plot of actual VR versus BRNN predicted VR, b predictors’ importance estimates using BRNN in VR prediction

The source rock maturity prediction using machine learning techniques has not been much explored previously (Hussein and Abdula 2018). The use of BRNN has shown very promising results for prediction of T_max and %VR as maturity indicators (Table 5). However, it can be noticed that the other ML techniques including BRNN with one hidden layer were unable to capture the relationship between the predictors and the T_max/%VR values. This suggests that the relationship between well-log data and rock maturity indicators is more complex which requires a high level of nonlinear modeling of the data that has been performed with multiple hidden layers of BRNN with different number of neurons in each layer.

The deep neural networks take longer time for training due to large number of parameters to be learnt. Hence, we experimented with a maximum of three hidden layers with various number of neurons in each hidden layer. The best results were found with two hidden layers and increasing the hidden layer did not help in improving the performance.

Currently, three different models were developed to predict TOC, T_max and VR separately. Unlike RF, BRNN is capable of predicting more than one target simultaneously. But it did not perform as well as RF in TOC prediction. Furthermore, the three predictions require different set of attributes. For instance, TOC required lithology information and not depth while VR does not require lithology information but requires depth. As it is common knowledge that depth is not a predictor of TOC prediction, it would create an unnatural model when depth is used in developing model for TOC prediction, even if it achieves high accuracy. It is important to choose good and relevant features that reflect the real world, for training the models.

Conclusion

This research has been conducted to demonstrate that ML techniques can be used for predicting TOC, T_max and %VR values in the absence or missing of geochemical data. Geochemical and well-log data have been collected from three different formations from the Cretaceous–Paleocene source rocks, Taranaki Basin, New Zealand. For TOC prediction, the best model achieved testing R² of 0.964 using RF with 40 trees. For T_max prediction, one-layer BRNN with 19 neurons in the hidden layers, respectively, achieved testing R² of 0.8283. A 2-layer BRNN with 3 and 5 neurons in the first and second hidden layers, respectively, achieved a testing R² of 0.6357 for VR prediction. No evidence of overfitting was found in all the best models used. Moreover, all five techniques performed exceedingly well for TOC prediction with R² above 0.96, BRNN with one hidden layer was the only ML technique able to achieve R² above 0.8 for T_max and BRNN with two hidden layers was the only ML technique able to achieve R² above 0.6 for %VR prediction.

Therefore, this research has provided very good empirical evidence that ML techniques such as RF and BRNN can produce good models for predicting with high accuracy not only organic matter richness TOC but also the maturity indicators T_max and %VR.

Geochemical data are few in availability due to the cost involved in conducting the necessary laboratory work as compared to the abundant well-log data. The challenge with using ML is the adequate availability of geochemical data to build a good model that can achieve prediction with high accuracy and confidence. When a good model has been obtained for prediction, it is possible to perform real-time TOC, T_max and VR prediction with high accuracy, directly from the same wells used for model training without deriving these values from geochemical laboratory work.