Introduction

Most of the condensate gas reservoirs are discovered in deep and tight formations with low permeability (Mohammadi et al. 2013). Complex physical and chemical phenomena in low-permeability condensate gas reservoir result in the change in gas well productivity (Zhang et al. 2014). When reservoir pressure is lower than dew point pressure, generation of condensate oil will decrease the gas relative permeability and well productivity (Li and Firoozabadi 2000; Rahimzadeh et al. 2016). In low-permeability reservoir, the absolute permeability is often sensitive to the stress and pore pressure (Sun et al. 2009; Shar et al. 2017). As effective stress increases, the absolute permeability will obviously decrease (Moghadam and Chalaturnyk 2016). Because of the influence of slippage effect, the apparent permeability of low-permeability reservoir will increase (Li et al. 2014; Wang et al. 2018). Furthermore, many experiments found that threshold pressure gradient existed in low-permeability reservoir (Guo and Wu 2007; Gao et al. 2008; Dou et al. 2014). Condensate blockage and relative permeability are research focuses in condensate gas reservoir (Farhoodi et al. 2019; Gholampour and Mahdiyar 2019). Slippage effect, stress sensitivity and threshold pressure gradient are usually considered in low-permeability and tight gas reservoir. However, all these phenomena including retrograde condensation, slippage effect, stress sensitivity and threshold pressure gradient which can influence gas well productivity are rarely considered simultaneously in low-permeability condensate gas reservoir.

Productivity analysis of condensate gas well is mainly based on the method of conventional dry gas well, including binomial and exponential productivity equation as well as empirical modified productivity equation based on them (Yan et al. 2006, 2007; Yuan et al. 2009; Xue et al. 2014). In recent years, productivity equation considering multiphase seepage has been paid more and more attention by scholars (Mokhtari et al. 2013; Huang et al. 2018; Li et al. 2018). With the further study of seepage mechanism of condensate gas reservoir, productivity analysis of condensate gas wells began to take into account the effects of many factors, such as phase change based on experiment and flash calculation, and adsorption effect of porous media (Shi et al. 2006, 2015; Qi et al. 2011; Lu et al. 2014; Jia et al. 2017). Seepage mechanism of low-permeability condensate gas reservoir is complicated because of its characteristics of low porosity, low permeability and phase change. Productivity analysis of low-permeability condensate gas well is not only different from conventional dry gas reservoirs but also different from conventional condensate gas reservoirs.

Combining the phase change characteristics of condensate gas reservoirs with the results of productivity studies of conventional dry gas reservoirs (Wu et al. 2008; Liao et al. 2012), according to steady seepage theory of condensate gas reservoir, the productivity equation of gas well in low-permeability condensate gas reservoir is established, which considers threshold pressure, stress sensitivity, slippage effect, high-speed non-Darcy effect and retrograde condensate effect. Because of nonlinear characteristics of the productivity equation, pseudo-pressure m(p), turbulence coefficient B and pseudo-threshold pressure coefficient C are calculated with numerical method to resolve the productivity equation. There are many factors influencing productivity of gas well in low-permeability condensate gas reservoir. Various factors have different influence degrees on gas well productivity. Orthogonal experiment design method is used to analyze the sensitivity, and the order of productivity influencing factors in low-permeability condensate gas well under different bottom hole pressures is known; thus, the corresponding measures can be taken to improve the productivity of gas well.

Establishment of productivity equation of low-permeability condensate gas well considering the influence of multiple factors

In the process of depletion development of condensate gas reservoir, once formation pressure is lower than dew point pressure of condensate gas, the change in phase behavior will happen and condensate oil will appear, which will result in the change in seepage rule in formation. Based on steady seepage theory of condensate gas, the following assumptions are made. ① Seepage of gas and condensate oil in formation abides by non-Darcy rule. For the gas, high-velocity turbulence effect near the well, threshold pressure gradient effect, stress sensitivity and slippage effect are considered. For the condensate oil, threshold pressure gradient and stress sensitivity are considered. ② The stress-sensitive relationship between reservoir permeability and effective stress is exponential. ③ The threshold pressure gradient of gas phase and condensate oil phase is the same. ④ The influence of capillary pressure is ignored. ⑤ Formation temperature is constant in the process of seepage. According to these assumptions, productivity equation of low-permeability condensate gas well considering the influence of multiple factors is established.

Considering the influence of high-speed non-Darcy and threshold pressure gradient, the equation of steady seepage of gas is as follows (Wang et al. 2012; He et al. 2013):

$$\frac{{{\text{d}}p_{\text{g}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{g}} }}{{k_{\text{g}} }}\upsilon_{\text{g}} + \beta_{\text{g}} \rho_{\text{g}} \upsilon_{\text{g}}^{2}$$
(1)

where pg is gas pressure, MPa; r is formation radius, m; λ is threshold pressure gradient, MPa/m; kg is gas permeability at pressure pg, μm2; μg is gas viscosity, mpa∙s; vg is gas velocity, m/s; ρg is gas density, kg/m3; βg is gas inertial resistance coefficient describing the effect of turbulence in porous media, 1/m.

Considering the influence of threshold pressure gradient, the equation of steady seepage of condensate oil is as follows:

$$\frac{{{\text{d}}p_{\text{o}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{o}} }}{{k_{\text{o}} }}\upsilon_{\text{o}}$$
(2)

where po is oil pressure, MPa; ko is oil permeability at pressure po, μm2; μo is oil viscosity, mpa s; vo is oil velocity, m/s.

Considering stress-sensitive effect, the relationship between permeability of low-permeability gas reservoir and effective stress is exponential, which is

$$k_{\infty } = k_{i} e^{{ - \alpha \left( {p_{i} - p} \right)}}$$
(3)

where k∞ is equivalent liquid permeability or absolute permeability at pressure p, μm2; ki is permeability at pressure pi, μm2; α is stress sensitivity coefficient, 1/MPa.

Considering slippage effect of gas seepage in porous medium, the relation between permeability k and absolute permeability k∞ is as follows

$$k = k_{\infty } \left( {1 + \frac{b}{{\bar{p}}}} \right)$$
(4)

where b is slippage factor, MPa; \(\bar{p}\) is average pressure

$$\bar{p} = \frac{{p_{i} + p_{\text{g}} }}{2}$$
(5)

According to 151 groups of experiment results of Luo et al. 2007, the relationship between slippage factor b and permeability is

$$b = 0.0315\left( {1000 \times k_{\infty } } \right)^{ - 0.6192}$$
(6)

Comprehensively considering multiple factors including threshold pressure, stress sensitivity, slippage effect and high-speed non-Darcy effect, gas seepage equation in low-permeability condensate gas reservoir is

$$\frac{{{\text{d}}p_{\text{g}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{g}} }}{{k_{i} k_{\text{rg}} e^{{ - \alpha \left( {p_{i} - p_{\text{g}} } \right)}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}\upsilon_{\text{g}} + \beta_{\text{g}} \rho_{\text{g}} \upsilon_{\text{g}}^{2}$$
(7)

where krg is gas relative permeability, fraction, dimensionless.

Considering the effect of threshold pressure and stress sensitivity, seepage equation of condensate oil in low-permeability condensate gas reservoir is

$$\frac{{{\text{d}}p_{\text{o}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{o}} }}{{k_{i} k_{\text{ro}} e^{{ - \alpha \left( {p_{i} - p_{\text{o}} } \right)}} }}\upsilon_{\text{o}}$$
(8)

where kro is oil relative permeability, fraction, dimensionless.

Substitute mass flow rate of gas phase Qg and oil phase Qo into Eqs. (7) and (8), the following equation is obtained

$$\frac{{{\text{d}}p_{\text{g}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{g}} }}{{k_{i} k_{\text{rg}} e^{{ - \alpha \left( {p_{i} - p_{\text{g}} } \right)}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}\frac{{Q_{\text{g}} }}{{2\pi rh\rho_{\text{g}} }} + \beta_{\text{g}} \rho_{\text{g}} \left( {\frac{{Q_{\text{g}} }}{{2\pi rh\rho_{\text{g}} }}} \right)^{2}$$
(9)
$$\frac{{{\text{d}}p_{\text{o}} }}{{{\text{d}}r}} - \lambda = \frac{{1000\mu_{\text{o}} }}{{k_{i} k_{\text{ro}} e^{{ - \alpha \left( {p_{i} - p_{\text{o}} } \right)}} }}\frac{{Q_{\text{o}} }}{{2\pi rh\rho_{\text{o}} }}$$
(10)

where βg can be calculated as follows (Shi et al. 2006):

$$\beta_{\text{g}} = \frac{0.003168}{{\left( {k_{i} k_{\text{rg}} e^{{ - \alpha \left( {p_{i} - p_{\text{g}} } \right)}} \left( {1 + \frac{b}{{\bar{p}}}} \right)} \right)^{1.25} \emptyset^{0.75} }}$$
(11)

where Qo, Qg are mass flow rate of oil and gas, kg/s; h is reservoir thickness, m.

Because the influence of capillary pressure is ignored,

$$p_{\text{g}} = p_{\text{o}} = p$$
(12)

Total mass flow rate is the sum of oil and gas mass flow rate

$$Q_{\text{t}} = Q_{\text{g}} + Q_{\text{o}}$$
(13)

Substitute Eq. (8), (9) and (12) into (13), then

$$\begin{aligned} Q_{\text{t}} &= 2\pi rhk_{i} e^{{ - \alpha \left( {p_{i} - p} \right)}} \left[ {\left( {\frac{{k_{\text{rg}} \rho_{\text{g}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{1000\mu_{\text{g}} }} + \frac{{k_{\text{ro}} \rho_{\text{o}} }}{{1000\mu_{\text{o}} }}} \right)}\right.\\&\quad\times\left.{\frac{{{\text{d}}\left( {p - \lambda r} \right)}}{{{\text{d}}r}} - \frac{{\beta_{\text{g}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{1000\mu_{\text{g}} }}\left( {\frac{{Q_{\text{g}} }}{2\pi rh}} \right)^{2} } \right] \end{aligned}$$
(14)

Through deformation, the following equation can be converted into

$$\begin{aligned} \frac{{Q_{\text{t}} }}{{2\pi rhk_{i} }}{\text{d}}r &= e^{{ - \alpha \left( {p_{i} - p} \right)}} \left( {\frac{{k_{\text{rg}} \rho_{\text{g}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{1000\mu_{\text{g}} }} + \frac{{k_{\text{ro}} \rho_{\text{o}} }}{{1000\mu_{\text{o}} }}} \right){\text{d}}\left( {p - \lambda r} \right)\\&\quad - \frac{{\beta_{\text{g}} e^{{ - \alpha \left( {p_{i} - p} \right)}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{1000\mu_{\text{g}} }}\left( {\frac{{Q_{\text{g}} }}{2\pi rh}} \right)^{2} {\text{d}}r \end{aligned}$$
(15)

Because fluid viscosity, density and relative permeability are functions of pressure p, in order to resolve the equation, the function f(p) is introduced, whose expressions can be written as

$$f\left( p \right) = e^{{ - \alpha \left( {p_{i} - p} \right)}} \left( {\frac{{k_{\text{rg}} \rho_{\text{g}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{\mu_{\text{g}} }} + \frac{{k_{\text{ro}} \rho_{\text{o}} }}{{\mu_{\text{o}} }}} \right)$$
(16)

Using Eq. (16), the integral of Eq. (15) is

$$\begin{aligned} \int\limits_{{p_{wf} }}^{{p_{e} }} f \left( p \right){\text{d}}p &= \int\limits_{{r_{w} }}^{{r_{e} }} {\frac{{1000Q_{\text{t}} }}{{2\pi rhk_{i} }}} {\text{d}}r + \int\limits_{{r_{w} }}^{{r_{e} }} {\frac{{\beta_{\text{g}} e^{{ - \alpha \left( {p_{i} - p} \right)}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{\mu_{\text{g}} }}}\\&\times \left( {\frac{{Q_{\text{g}} }}{2\pi rh}} \right)^{2} {\text{d}}r + \lambda \int\limits_{{r_{w} }}^{{r_{e} }} f \left( p \right){\text{d}}r \end{aligned}$$
(17)

The pseudo-pressure expression of gas–liquid two phases is defined as

$$m\left( p \right) = \mathop \int \limits_{0}^{p} f\left( p \right){\text{d}}p$$
(18)

Suppose the ratio of gas mass flow rate to total mass flow rate in formation is \(M = Q_{\text{g}} /Q_{\text{t}}\), and convert total mass flow rate into volume flow under standard condition through relationship \(Q_{\text{t}} = Q_{\text{sc}} \rho_{\text{sc}}\), then Eq. (17) is written as

$$\begin{aligned} m\left( {p_{e} } \right) &- m\left( {p_{wf} } \right) - \lambda \mathop \int \limits_{{r_{w} }}^{{r_{e} }} f\left( p \right){\text{d}}r = \frac{{\rho_{\text{sc}} }}{{1.728 \times 10^{2} \pi hk_{i} }}\\& \quad \ln \frac{{r_{e} }}{{r_{w} }}Q_{\text{sc}} + \frac{{\rho_{\text{sc}}^{2} \mathop \int \nolimits_{{r_{w} }}^{{r_{e} }} \frac{{\beta_{\text{g}} e^{{ - \alpha \left( {p_{i} - p} \right)}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{\mu_{\text{g}} }}\left( {\frac{M}{r}} \right)^{2} {\text{d}}r}}{{2.986 \times 10^{10} \left( {\pi h} \right)^{2} }}Q_{\text{sc}}^{2} \end{aligned}$$
(19)

where ρsc is density of condensate gas under standard conditions, kg/m3; Qsc is total production rate of condensate gas well under standard conditions, m3/day.

Equation (19) is the productivity equation of low-permeability condensate gas well considering the influence of multiple factors including retrograde condensation effect, threshold pressure, slippage effect and stress sensitivity. It can also be abbreviated to

$$m\left( {p_{e} } \right) - m\left( {p_{wf} } \right) - C = AQ_{\text{sc}} + BQ_{\text{sc}}^{2}$$
(20)

Solution of productivity equation of low-permeability condensate gas well considering the influence of multiple factors

To calculate gas well productivity by Eq. (19), the key is to solve three integral terms including pseudo-pressure m(p), turbulence coefficient B and pseudo-threshold pressure coefficient C.

Solution of pseudo-pressure m(p)

On the basis of fluid flash calculation results of condensate gas reservoir, the method of numerical integration is used to calculate the pseudo-pressure

$$m\left( p \right) = \mathop \sum \limits_{j = 1}^{n - 1} \frac{1}{2}\left( {f\left( {p_{j} } \right) + f\left( {p_{j + 1} } \right)} \right)\left( {p_{j} - p_{j + 1} } \right)$$
(21)

Solution of coefficients B and C in the productivity equation

The coefficients B and C in the productivity equation are integrals of radius, and the variation of function value with radius in integral term is caused by the change in formation pressure. Therefore, the exact relation between pressure p and radius r must be obtained first, and then, the integral can be calculated. According to steady seepage theory, the relationship between reservoir pressure and radius under different bottom hole pressures can be obtained.

$$r = r_{w}^{\prime } \left( {\frac{{r_{e} }}{{r_{w} }}} \right)^{{\frac{{m\left( p \right) - m\left( {p_{wf} } \right)}}{{m\left( {p_{e} } \right) - m\left( {p_{wf} } \right)}}}}$$
(22)

According to Eq. (22), the pseudo-pressure at any radius under different bottom hole pressures is obtained firstly, and then, the method of numerical integration shown in Eq. (21) is used to calculate B and C. Because the influences of pseudo-threshold pressure and turbulence term on fluid seepage are small, coefficients B and C can also be solved by using the approximate method of definite integral, which are shown as follows

$$\begin{aligned} B &= \left( {\frac{{\rho_{\text{sc}} }}{2\pi h}} \right)^{2} \times \frac{1}{2}\left( {\left( {\frac{{\beta_{\text{g}} e^{{ - \alpha \left( {p_{i} - p} \right)}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{\mu_{\text{g}} }}\left( {\frac{M}{r}} \right)^{2} } \right)|_{{r = r_{e} }} }\right.\\&\left.\quad {-\, \left( {\frac{{\beta_{\text{g}} e^{{ - \alpha \left( {p_{i} - p} \right)}} k_{\text{rg}} \left( {1 + \frac{b}{{\bar{p}}}} \right)}}{{\mu_{\text{g}} }}\left( {\frac{M}{r}} \right)^{2} } \right)|_{{r = r_{w} }} } \right)\left( {r_{e} - r_{w} } \right) \end{aligned}$$
(23)
$$C = \lambda \mathop \int \limits_{{r_{w} }}^{{r_{e} }} f\left( p \right){\text{d}}r = \lambda \frac{1}{2}\left( {f\left( p \right)|_{{r = r_{e} }} - f\left( p \right)|_{{r = r_{w} }} } \right)\left( {r_{e} - r_{w} } \right)$$
(24)

Therefore, Qsc is calculated to be

$$Q_{\text{sc}} = \frac{{ - A + \sqrt {A^{2} + 4B\left[ {m\left( {p_{e} } \right) - m\left( {p_{wf} } \right) - C} \right]} }}{2B}$$
(25)

Example calculation

Analysis of single factor impact

Tested components and compositions of condensate gas are shown in Table 1. Condensate oil content of a condensate gas reservoir is 303 g/cm3. The data are from flash experiment test result of condensate gas system samples in formation. It is seen that the contents of intermediate and heavy hydrocarbon are low, which is a condensate gas system with low medium content of condensate oil and high gas–oil ratio. Thickness of gas pay h is 36.20 m, drainage radius re is 500 m, temperature of gas reservoir Ti is 165.3 °C, original formation pressure pi is 38.64 MPa, dew point pressure pd is 35.92 MPa, absolute permeability ki is 1.23 × 10−3μm2, porosity ϕ is 0.09, stress sensitivity coefficient α is 0.059/MPa, irreducible water saturation Swc is 0.302, and threshold pressure gradient λ is 0.004 MPa/m. The density and viscosity of gas and liquid phase of the condensate gas system under different pressures in Table 2 are from phase equilibrium calculation based on fitting of PVT experiments including flash separation experiment, equal composition expansion experiment and constant volume depletion experiment through PVTi software of Eclipse.

Table 1 Tested components and compositions of condensate gas
Full size table
Table 2 Statistical table of gas–liquid parameters under different pressures of fluid in a condensate gas reservoir
Full size table

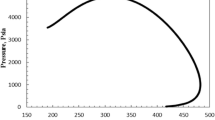
Relative permeability curve of gas and condensate oil is shown in Fig. 1. In low-permeability condensate gas reservoir, the interface phenomenon between fluid and porous medium is very obvious because of fine rock particles and small pores. Because the capillary force is usually the resistance of condensate gas, the flow of gas phase will be difficult after two phases of condensate oil and gas appear in formation. Moreover, pore medium has a strong adsorption effect on condensate oil and gas. After condensate oil generates, free oil phase, gas phase and adsorbed condensate oil coexist in formation, but only the free oil and gas phase can flow in porous medium. As a whole, the maximum relative permeability of condensate oil and gas at end point saturation is low. Relative permeability curves in Fig. 1 means that gas saturation at the equal-permeability point is on the right side of the two-phase flow zone, which indicates that the flow resistance of gas is large because of retrograde condensation. Gas relative permeability and gas well productivity is obviously influenced by condensate oil saturation.

Fig. 1
figure 1

Oil and gas relative permeability curve of a condensate gas reservoir

Full size image

According to the above principles and data, the two-phase pseudo-pressure function curve considering different factors is calculated with Eq. (21), which is shown in Fig. 2. It is indicated that slippage effect increases apparent permeability; thus, the pseudo-pressure increases. The apparent permeability decreases with the increase in effective stress, so pseudo-pressure decreases. The stress sensitivity has greater influence on pseudo-pressure calculation results under the combined action of the two factors.

Fig. 2
figure 2

Two-phase pseudo-pressure function curve considering different influence factors

Full size image

According to calculation results of pseudo-pressure function, the productivity of a condensate gas well considering different influence factors calculated with Eq. (20)–(25) is shown in Fig. 3 and Table 3. The results show that with the decrease in bottom hole pressure, the increase in condensate gas well production rate is near linear first, and then, the increase is getting slower and slower. Various factors have different influence degrees on productivity of low-permeability condensate gas well. Based on the production rate considering phase change, the calculated average production rate will increase by 4.16% when considering phase change and slippage effect simultaneously. If phase change and stress sensitivity effect are considered simultaneously, the calculated average production rate will decrease by 14.82%. If phase change, tress sensitivity and slippage effect are considered simultaneously, the calculated average production rate will decrease by 11.30%. If phase change, tress sensitivity, slippage and threshold pressure effect are considered simultaneously, the calculated average production rate will decrease by 26.81%. Therefore, if only the effect of phase change is considered, the calculation of condensate gas well productivity will generate great error, and more factors should be taken into account in actual application.

Fig. 3
figure 3

Comparison diagram of productivity calculation results of a condensate gas well considering different factors

Full size image
Table 3 Comparison table of productivity calculation results of a condensate gas well considering different factors
Full size table

Multifactor sensitivity analysis based on orthogonal design

According to the above research results, the factors influencing productivity equation of condensate gas well are analyzed from the aspects of phase change, slippage effect, stress sensitivity effect and threshold pressure gradient effect. In order to analyze sensitivity of various factors, an orthogonal test with equal level 4 factors is designed, which is shown in Table 4. There are nine cases according to orthogonal design table L9(34). Based on the productivity equation of low-permeability condensate gas well under the influence of multiple factors, the productivity of each case is calculated. The results are shown in Tables 5 and 6.

Table 4 Level table of influencing factors for productivity of a low-permeability condensate gas well
Full size table
Table 5 Orthogonal experiment result table L9(34) with 4 factors influencing productivity of a low-permeability condensate gas well (Pwf = 12 MPa)
Full size table
Table 6 Orthogonal experiment result table L9(34) with 4 factors influencing productivity of a low-permeability condensate gas well (Pwf = 20 MPa)
Full size table

In Tables 5 and 6, k1, k2, k3 are average values of production rate at the same level for each factor. R is the difference between the maximum and the minimum of k1–k3. The bigger the R is, the more obvious the influence of this factor is. Results indicate that in the range of threshold pressure gradient λ = 0–0.004 MPa/m, stress sensitivity coefficient α = 0–0.06/MPa, slippage factor b = 0–0.6 MPa, condensate oil saturation So = 0–6%, when bottom hole pressure is 10–17.5 MPa, the order of productivity influencing factors in low-permeability condensate gas wells is stress sensitivity > retrograde condensate phase change > threshold pressure gradient > slippage effect. When bottom hole pressure is 17.6–24.7 MPa, the order of productivity influencing factors in low-permeability condensate gas wells is stress sensitivity > threshold pressure gradient > retrograde condensate phase change > slippage effect. When bottom hole pressure is 24.8–33.8 MPa MPa, the order of productivity influencing factors in low-permeability condensate gas wells is threshold pressure gradient > stress sensitivity > retrograde condensate phase change > slippage effect. Within different ranges of bottom hole pressure, corresponding measures can be taken to improve the productivity of gas well according to the key sensitive factors affecting the productivity of low-permeability condensate gas well.

Conclusions

  1. 1.

    In low-permeability condensate gas reservoir, because of condensate banking or blockages near the well bore area, two-phase flow of gas and condensate oil arises in the reservoir. The relative permeability and mobility of each fluid are different, and they compete for flow toward the well. Compared to conventional dry gas reservoir, seepage mechanism is more complicated in low-permeability condensate gas reservoir, where two-phase flow with various non-Darcy effects of gas and condensate oil should be considered simultaneously.

  2. 2.

    The binomial productivity equation with the form of pseudo-pressure in low-permeability condensate gas well is established considering the comprehensive effect of multiple factors including threshold pressure gradient, stress sensitivity, slippage effect, retrograde condensate effect, high-speed non-Darcy effect. The integrals of pseudo-pressure, turbulence factor and pseudo-threshold pressure are calculated with numerical method to resolve the productivity equation.

  3. 3.

    The productivity of an example well is calculated by considering different factors. Results indicate that slippage effect increases apparent permeability; thus, the pseudo-pressure and gas well production rate increase. Retrograde condensate effect decreases gas relative permeability and gas well production. The apparent permeability decreases with the increase in effective stress, so pseudo-pressure and gas well production rate decreases. Threshold pressure gradient reduces the production pressure difference; therefore, the productivity of gas well decreases.

  4. 4.

    Based on orthogonal experiment design, the sensitivity factors affecting productivity of low-permeability condensate gas well are analyzed in different ranges of bottom hole pressure. The research lays a theoretical foundation for taking measures to improve gas well productivity in the gas field.