Introduction and literature review

At present, in order for unconventional reservoirs in North America to be commercially productive, hydraulic fracturing is required. One of the standard procedures to produce these reservoirs is through multistage hydraulically fractured horizontal well (Wang 2015). A stimulated rock volume (SRV) is created after a tight gas reservoir is hydraulically fractured. The hydraulic fracture–natural fractures interaction (both open and reopened) within the SRV contributes to its high permeability and large drainage area (Guo et al. 2014). The SRV’s dimensions and permeability are the important parameters that dictate the reservoir’s recovery. Microseismic monitoring can provide insights into the SRV. Previous studies have linked the SRV to the microseismic cloud (Mayerhofer et al. 2010); however, there is an evidence that a simple correlation of the calibration of the seismically stimulated volume inferred from the microseismic cloud requires additional analysis (Cipolla and Wallace 2014). Moreover, the interactions of hydraulic and natural fractures require further understanding.

The permeability of a reservoir containing natural fracture was estimated by Oda (1986) through the SRV dimension and the cubic law. Rahman et al. (2002) suggest that the permeability of SRV was effected by fracture density, stimulation pressure and stresses within the reservoir. The authors created a model that considers shear slippage and the natural fractures propagation. An iterative method to obtain SRV permeability through the matching of computed SRV size with SRV determined from microseismic data was developed by Ge and Ghassemi (2011). The authors then used this permeability in determining pore pressure, stress distribution and the SRV. A semi-analytical equation was proposed by Bahrami et al. (2012). The equation models the fracture permeability taking into account the fracture spacing, fracture aperture and well-test permeability. Johri and Zoback (2013) proves that the slip of the natural fractures during hydraulic fracturing enhances the permeability of fracture. A coupled reservoir-geomechanics model was developed by Nassir (2013) to determine SRV permeability. The author found that at high injection rates, the maximum permeability enhancement occurs.

Some of the latest studies in hydraulic fracturing by using finite element analysis were conducted by Chen et al. (2017) where they created finite element model to investigate the interaction between hydraulic fracture and preexisting natural fracture. However, as the crack utilizes cohesive elements, the crack path needs to be predetermined. The fracture will only grow along and within predefined path. Gao and Ghassemi (2018) utilized finite element modeling to analyze hydraulic fracture propagation in layered rock. Similarly, they used cohesive element to define the crack which requires the pathway of the hydraulic fracture to be predetermined.

Despite considerable previous research undertaken to determine relationships among SRV permeability and dimensions, original rock permeability, natural fracture characteristics and the relationships in the context of geomechanical properties remain unclear. In this study, fluid injection and the changing of pressure is modeled by a three-dimensional (3D) finite element analysis (FEA) geomechanic single-phase flow within the SRV. The SRV is assumed to be a linear elastic medium with increased permeability and is isotropic. The semi-analytical method uses effective permeability to determine the distance between fractures, fracture aperture and total stress changes.

Since the 1980s, numerical and experimental studies to investigate the hydraulic fractures–natural fractures interactions have been conducted. Blanton (1982) reveals the tendency of hydraulic fracture crossing of preexisting fractures occurs only under high angle of approach and high stress difference. Warpinski and Teufel (1987) show that interaction between hydraulic fractures–preexisting fractures is influenced among other by reservoir stresses difference, distance between preexisting fractures, the pressure during the hydraulic fracturing and permeability. Shimizu et al. (2014) show that high approach angle and low permeability of the preexisting fractures result in limited hydraulic fracture–natural fractures interaction. Universal Distinct Element Code method has been employed by Pirayehgar and Dusseault (2014) to reveal that the branching occurs when the stress ratio is small. Kim and Schechter (2007) use a fracture network model, outcrop maps, computer tomography imaging, image logs and fracture data of cores to determine the fracture aperture. Yu and Aguilera (2012) solves a three-dimensional pressure diffusion equation in order to determine the lowering of pressure inside the SRV and to determine an effective hydraulic diffusivity coefficient for flow within the SRV by using an analytical model developed. Izadi and Elsworth (2014) utilizes the cubic law in determining the pressure drop within the SRV. There are analytical models to estimate aperture and extent of hydraulic fractures using the Young’s modulus (Khristianovitch and Zheltov 1955; Geertsma and de Klerk 1969; Perkins and Kern 1961) and Poisson’s ratio (Valko and Economides 2001). Bratton (2011) shows that the fracture complexity is affected by the anisotropy of the in situ stresses where less reservoir stress anisotropy results in a less distinct preference of direction of the hydraulic fracture network.

Several authors presented their work to determine the fracture aperture estimation during drilling. Sanfillippo et al. (1997) estimate the fracture aperture using the mud losses and the Poiseuille Law. Their methods can only accommodate the lowest mud losses volume equal to 20 L and only considers the natural fractures not the induced fractures. Lietard et al. (1996) determine the fracture aperture during drilling from the mud losses in fractures. Geertsma and de Klerk (1969) identify the hydraulic fracture width to be dependent on fracture length and height, shear modulus, injection rate and fluid viscosity. This method is limited as the fracture permeability is not considered in calculating the fracture aperture.

Based on the previous methods limitations, this work is integrating the finite element analysis results on the stimulated reservoir volume permeability, the injected volume, the Darcy law and the cubic law to identify the natural fracture and hydraulic fracture aperture, numbers and spacing.

Hoadley field properties

This study focuses on a tight gas reservoir located in the glauconitic formation. The formation of interest in the Hoadley Field Rimbey, Alberta, Canada, has thickness of about 43 m at a total vertical depth (TVD) of 1892 m (Rafiq et al. 2016). As the maximum stress is the maximum horizontal stress, the intermediate stress is the vertical stress and the minimum stress is the minimum horizontal stress; the fault regime of this field is strike slip. The maximum horizontal stress orientation is 48°NE. The Medicine River coal formation with 5 m thickness and the Mannville formation with 80 m thickness overlie the glauconitic formation. The Ostracod Formation with 87 m thickness underlies the glauconitic formation. The average permeability of the glauconitic formation is determined to be approximately 0.07 mD from the study well’s pressure buildup test and the nearby well’s core test (Core Laboratories – Canada Ltd. 1985. Microseismic data (Eaton et al. 2014) documentation and inference of Mohr–Coulomb failure criterion predicted that the natural fracture has 30° inclined angle relative to the maximum horizontal stress. Table 1 listed the properties.

Table 1 Initial formation properties
Full size table

The dynamic modulus properties are anticipated to have higher values than the static modulus presented by Jizba et al. (1990) as they are calculated from sonic logs. Microseismic monitoring data from Maulianda et al. (2014) are used to estimate the SRV dimensions and are listed in Table 2.

Table 2 Stimulated rock volume (SRV) dimensions
Full size table

Finite element model

The software used to simulate the finite element model is called Abaqus, which is a software for finite element analysis. The modeling started by the creation of model geometry, in which the different formations are created without their properties by partitioning. Following that, the properties of each formation are created separately and it is assigned to the created geometry according to their respective sections. The initial and boundary conditions, which include the stresses, pore pressure and pumping step definition, are then applied onto the model. The model is then meshed following which the simulation can be run. The following sections describe in more details on the model created.

Model geometry

The model, displayed in Fig. 1, has the dimensions of: 240 m length (x-axis) and 240 m width (y-axis). It consists of four layers block. The total thickness of the model is 215 m. This includes the 87 m Ostracod formation, the 43 m target glauconitic formation, the 5 m Medicine River coal layer and the 80 m Manville formation. The domain’s bottom surface is located at 2000 m depth. From the microseismic data, it was identified that the SRV half-length is 87 m (x-axis), while the width is 30 m (y-axis). The total height of the SRV is 60 m (z-axis). To take the stress field into consideration, the model size is made to be three times of the stimulated reservoir volume length.

Fig. 1
figure 1

Meshing of the finite elements for hydraulic fracturing (SRV) simulation

Full size image

To take into account SRV and non-SRV sections, the model is partitioned into seven sections. These seven sections are the Medicine River—non-SRV and SRV, Glauconitic—non-SRV and SRV, the Mannville—non-SRV and SRV, and the Ostracod—non-SRV. Dimensions of the SRV are determined from microseismic data as described in Maulianda et al. (2014). The model assumes that during the fluid injection, the SRV has a relatively high permeability. Each formation in the model has its own Poisson’s ratio, permeability, Young’s modulus, density, void ratio and host fluid specific weight, as listed in Table 1. The dynamic Young’s modulus and dynamic Poisson’s ratio are derived from sonic log data.

As the model is symmetrical across the x = 0 plane and y = 0 plane, quarter of the geometry is created with remaining three quarters represented by symmetrical planes. The model is discretized into a total of 9676 tetrahedral finite elements during the meshing. The meshing is made into two distinct sections. Firstly, the coarser section which make the formations, with mesh size equivalent to 16 m. Secondly, the finer section which covers the SRV, which have a mesh size equivalent to 5 m.

Initial conditions and boundary conditions

Parameters as follows are defined to specify the initial conditions: (a) the effective stresses, (b) the void ratio and (c) the pore pressure. Initial static equilibrium was achieved by applying the following loads on the domain: (a) The overburden stress of 43 MPa which is applied on the top surface and was considered to be equal across the model top surface and (b) gravitational acceleration load of 9.8 m/s2 applied on the whole in the negative z-direction.

In step two, a hydraulic fracture pumping stage is simulated. The injection with a total duration of 2250 s is divided into three steps. The durations of step one is 1 s, step two is 10 s and step three is 2239 s. Steps one and two are divided into ten equivalent steps. For step three, each time step is equivalent to 5 s. Smaller time increments are applied in the earlier stage to study the consolidation when the loads are applied. In step two, injection velocity equivalent to flow rate of 5 m3/min is introduced to the surface representing the injection port. Boundary conditions representing the initial pore pressure are also introduced. By using a machine with specification of 2.2 GHz, 4-core and 16 GB of memory, an average of 1.5 h wall-clock time is required for the simulation.

Results and discussion

Determination of the SRV effective permeability

An iterative search was done by changing the SRV effective permeability until the simulated injected bottom-hole pressure matches the field average fracture propagation pressure. The average fracture propagation pressure from the field to be matched is equivalent to 27.6 MPa. The model only attempts to match the fracture propagation pressure which is taken at the final injection time as deformation and fracture initiation pressure are not taken into account. From the iterative search, the effective permeability of 23.4 mD is found to give the best match to the bottom-hole pressure from the field data (permeability assumed to be isotropic) to match the SRV dimensions. The matched case is referred to as Case 1.

In determining the SRV dimensions effect on the effective permeability (arising from uncertainties of the microseismic data), a simulation was done in which each SRV dimension was reduced by 10% leading to an overall SRV volume reduction in 27%. This case is referred to as Case 2. The effective permeability for Case 2 required to match the field data is equal to 45.8 mD. Figure 2 also shows that in comparison with Case 1’s bottom-hole injection pressure gradient of 4.9 kPa/s, Case 2 has a higher gradient at 6.6 kPa/s at the early times (0 s) and late times (2002 s). However, the bottom-hole injection pressure gradient at the late time is similar for both Case 1 and Case 2.

Fig. 2
figure 2

Field bottom-hole injection pressure and FEA predicted results

Full size image

A grid sensitivity was conducted: Case 3 is identical to Case 1 except the dimensions of the grid were reduced by 63%. As shown in Fig. 2, the pore pressure profile changes by 0.17%, whereas the deformation changes by a maximum value of 0.7% and the maximum change of the stress is less than 0.1%. This demonstrates that the dimensions of the original mesh are sufficiently resolved.

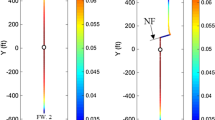
The distribution of pore pressure within and around the SRV at various injection times for Case 1 are shown in Fig. 3. The pre-calculation distribution of pore pressure (initial condition) shown in Fig. 3a, b shows the initial distribution of pore pressure after applying the reservoir stresses. The distribution of pore pressure after 1 s, 551 s and 1101 s of fluid injection is displayed in Fig. 3c–e, respectively. After fluid injection for 1101 s, the targeted bottom-hole pressure is almost reached. Lastly, Fig. 3f shows the maximum pore pressure at the injection port after 2250 s; the pore pressure is 27.6 MPa, whereas at the SRV boundary, it is equal to 20.1 MPa.

Fig. 3
figure 3

Case 1 (k = 23.4 mD): a pore pressure (Pa) following initial condition application, b pore pressure (Pa) following reservoir stresses and boundary conditions application on the domain, ct = 1 s, dt = 551 s, et = 1101 s and f end of injection at t = 2250 s

Full size image

The SRV’s targeted bottom-hole pressure is obtained earlier in Case 2 as shown in Fig. 3f, 4f. Similar to Case 1, in Case 2, as the fluid is injected, the pressure rises within the SRV, but the pressure is more uniform.

Fig. 4
figure 4

Case 2 (k = 45.9 mD): a pore pressure (Pa) following initial condition application, b pore pressure (Pa) following reservoir stresses and boundary conditions application on the domain, ct = 1 s, dt = 551 s, et = 1101 s and f end of injection at t = 2250 s

Full size image

Effect of SRV Young’s modulus on its effective permeability

To investigate the effect of SRV Young’s modulus on effective permeability, parametric studies were conducted. The SRV Young’s modulus was decreased to 90, 80 and 70% of the original Young’s modulus values. The sensitivity study for Case 1 shows that when reduction in 90, 80 and 70% of the SRV Young’s modulus is made, the final bottom-hole pressures are 27.0, 26.4 and 25.8 MPa, respectively. For Case 2, decreasing the SRV Young’s modulus to 90, 80 and 70%, the final bottom-hole pressures are 26.8, 26.0 and 25.1 MPa, respectively.

Additional parametric studies were also conducted to find the effective permeability which matches the final bottom-hole pressure for the decreased Young’s modulus values that give an injection pressure of 27.6 MPa. In Case 1, 70, 80 and 90% of the base Young’s modulus resulted in matched effective permeability values of 18.4, 20.0 and 21.5 mD, respectively. For Case 2, 70, 80 and 90% of the base Young’s modulus resulted in matched permeability values of 27.0, 35.8 and 39.8 mD, respectively.

The parametric studies show that with a given injection rate and volume, the injection pressure decreases with increasing compressibility or decreasing Young’s modulus. To maintain the same injection pressure, the SRV effective permeability has to be reduced. The reduction in effective permeability of the SRV could imply reduction in fracture aperture or spacing. Reduction in the SRV size leads to the effective permeability increase to maintain the same injectivity.

Changes in Total Stresses in SRV due to Injection for Porous Medium

The distributions of the effective maximum horizontal stresses, effective minimum horizontal stress and effective vertical stress in the SRV length, width and height are plotted in Figs. 5, 6 and 7 for Case 1 of the base Young’s modulus. The pore pressure and effective stresses are generated by Abaqus throughout the model. Terzaghi (1925) effective stresses equation is used to calculate the total stresses. The results reveal that there is reduction in pore pressure from the injection port to a distance of about 10 m along the SRV, and the pressure drop is relatively small from that point on to the SRV boundary (Figs. 8a, 9a, 10a). The increases in the total maximum horizontal stress, the total minimum horizontal stress and the total vertical stress occur over the first 10 m from the injection port (Figs. 8b, 9b, 10b). These total stress increases are caused by the poro-elastic effect and fluid injection. Vermylen (2011) explained the poro-elastic effect and fluid injection by stating that the total stress changes in reservoir due to hydraulic fracturing are attributed to three general causes: (a) tensile hydraulic fracture creation, (b) increased pore pressure in the reservoir due to the effects of poro-elastic when there are fluid leakage from the hydraulic fracture and (c) propagation of the hydraulic fracture. From the injection port to a distance of 10 m from it, there are changes of the total stresses, and the changes are relatively small from that point to the SRV boundary as shown in Fig. 8b. The total maximum horizontal stress increased to 49 MPa and 61 MPa after the hydraulic fracture near the injection port. Over 1 s time period, no changes observed between 10 m from the injection port to the boundary of the SRV. However, at late injection time of 551, 1101 and 2250 s, there are small increases in the total maximum horizontal stress between 10 m from the injection port to the boundary of the SRV, between 50 MPa and 56.5 MPa (Fig. 8b). In Abaqus, the convention is to use negative (−ve) number to describe compression stress, while positive (−ve) number is used for tensile stress.

Fig. 5
figure 5

Case 1 (k = 23.4 mD): Effective maximum horizontal stress versus distance along the SRV length from the injection port at different injection times

Full size image
Fig. 6
figure 6

Case 1 (k = 23.4 mD):  Effective minimum horizontal stress versus distance along SRV width from the injection port at different injection times

Full size image
Fig. 7
figure 7

Case 1 (k = 23.4 mD): Effective vertical stress versus distance along SRV height from the injection port at different injection time

Full size image
Fig. 8
figure 8

Case 1 (k = 23.4 mD):  a Pore pressure versus distance and b total maximum horizontal stress versus distance along SRV length from the injection port at various injection times

Full size image
Fig. 9
figure 9

Case 1 (k = 23.4 mD): a Pore pressure versus distance and b total minimum horizontal stress versus distance along SRV length from the injection port at various injection times

Full size image
Fig. 10
figure 10

Case 1 (k = 23.4 mD): a Pore pressure versus distance and b total vertical stress versus distance along SRV height above injection ports at various injection times

Full size image

The ratio of increase in total stress to increase in pore pressure is about 0.6. Similar trends in pore pressure and total stresses responses due to injection are observed in other two perpendicular directions (Figs. 9, 10). In this study, the changes in the total stresses might be overestimated because of the assumption that the Biot’s constant is equivalent to 1. The total in situ stress changes due to pore pressure will be reduced for the glauconitic formation as the Biot’s constant should be less than unity.

Profiles of the effective stresses for Case 2 are shown in Figs. 11, 12 and 13. The results are similar to those of Case 1. The main difference between Cases 1 and 2 is that the pressure drops between the injection point and SRV boundary are 7.52 and 3.84 MPa, respectively. This is due to the elevated permeability used in Case 2. The horizontal stresses at the SRV boundaries at 2250 s are higher for Case 2 than for Case 1. The vertical stress is smaller for Case 2 by 0.8 MPa. This suggests that smaller SRV dimensions result in a higher stress increase (with all other properties are held constant).

Fig. 11
figure 11

Case 2 (k = 45.9 mD): Effective maximum horizontal stress versus distance along SRV length from the injection port at different injection times

Full size image
Fig. 12
figure 12

Case 2 (k = 45.9 mD): Effective minimum horizontal stress versus distance along SRV width from the injection port at different injection times

Full size image
Fig. 13
figure 13

Case 2 (k = 45.9 mD): Effective vertical stress versus distance along SRV height from the injection port at different injection times

Full size image

Determination of fracture aperture using Cubic Law

The cubic equation is used to analytically calculate the pore pressure gradient along a planar fracture as shown in Eq. (1) (Brown 1987).

$$QL \, = \, - \frac{{d^{3} }}{12\mu }\frac{{{\text{d}}P}}{{{\text{d}}x}}$$
(1)

where \(L\) is the fracture width normal to fluid flow direction, \(Q\) the flow rate, P the fluid pressure, d is the fracture aperture, µ the fluid viscosity and x the distance.

Figure 14a shows the SRV changed fracture aperture and half-length for Case 1 and Fig. 14b for Case 2. The aperture is changed from 1.43 to 7 mm for Case 1 with maximum SRV half-length of 87 m. The simulated pore pressure matched 20.1 MPa at the SRV boundary when the fracture aperture is 1.43 mm. Figure 14b also shows that fracture aperture is changed for Case 2 from 1.78 to 7 mm with the maximum SRV half-length of 78 m. The simulated pore pressure matched 23.8 MPa at the SRV boundary when the fracture aperture is 1.78 mm. The differences between the results of cubic law model and pore pressure of the finite element are that steady state flow is assumed for the cubic law model, whereas transient flow is assumed for the finite element modeling. In addition, geomechanics effect is not considered in the cubic equation.

Fig. 14
figure 14

Pore pressure versus distance using the cubic law equation for a Case 1 and b Case 2. d = fracture aperture in mm

Full size image

Fracture characteristics determination using semi-analytical approach

Fracture characteristics are calculated from a developed semi-analytical approach in this section. Leak-off is neglected by the semi-analytical. Major and minor fracture sets are assumed to create the fracture network within the SRV. The natural fractures are represented by the minor fracture. The hydraulic fractures (major fractures) are assumed to propagate through the SRV length, while the natural fractures (minor fractures) are inclined 30° with respect to the maximum horizontal stress as shown in Fig. 15. Since the major fractures are assumed to connect the SRV boundaries, they contribute to both the SRV enhanced permeability and injected volume. On the other hand, as it is assumed that the minor fractures do not connect to the SRV boundaries and is a dead end, they assumed to contribute to the injected volume only. The approach assumes that major fractures (perpendicular to Sh) are created by the intersection of hydraulic fractures and natural fractures. Therefore, it is assumed that the hydraulic fractures and natural fractures are connected and the volume of the injected fracture fluid is contributed by it.

Fig. 15
figure 15

Top view showing minor and major fractures

Full size image

Calculating the major fracture number, minor fracture number, fracture spacing and fracture aperture requires two criteria. The two criteria used are the mass conservation criteria and equivalent flow characteristics criteria:

$$\overline{k}_{\text{SRV}} A_{\text{SRV}} = \sum \overline{k}_{\text{fracture}} A_{\text{fracture}} .$$
(2)
$${\text{Injected}}\;{\text{volume}} = {\text{Fracture}}\;{\text{volume}} .$$
(3)

In Eq. (2), \(\overline{k}_{\text{SRV}}\) is effective permeability obtained from FEA, while ASRV is area of flow of the SRV, respectively. \(\overline{k}_{\text{fracture}}\) is the cubic law-derived permeability, and Afracture is the flow area of each major fracture. An assumption of accumulation of all of the injected volume in both the major and minor fractures is used in Eq. (3) as shown in Fig. 15. The procedure used for the calculation of the fracture aperture, numbers and spacing is shown in Fig. 16.

Fig. 16
figure 16

Procedure to compute fracture aperture, number and spacing

Full size image

The increase in fracture aperture for Case 1 from 1 to 2.1 mm results in a decrease in the major fractures numbers and loss of pressure along the SRV length (Fig. 17a). However, increasing fracture aperture from 1 to 1.43 mm results in the increase in the number of minor fracture; a further increase in fracture aperture induces a decrease in the number. This is due to the need of the total injected volume to match the total fracture volume of both the major and minor fractures. The increase in fracture aperture for Case 2 from 1.1 to 2.25 mm results in the decrease in the major fractures numbers and pressure drop along the SRV length while increasing the number of minor fractures until the fracture aperture is 2.1 mm, and then, it decreases (Fig. 17b). Table 3 lists results for cases where the effective permeability of the SRV is reduced.

Fig. 17
figure 17

Relationship among fractures number, fracture aperture and fracture pressure gradient for a Case 1 and b Case 2. The apertures for the minor and major fractures are assumed to be equal

Full size image
Table 3 Young’s modulus and SRV effect on the major and minor fractures numbers
Full size table

For a constant fracture aperture, smaller effective permeability results in lower number of the major fractures and greater the number of minor fractures. The response obtained for Case 2 is similar to those in Case 1. The fracture characteristics for Case 1 are as follows: 5 major fractures with spacing of 12 m, and 12 minor fractures with spacing of 14.5 m and fracture aperture of 1.43 mm. The fracture characteristics for Case 2 are as follows: 4 major fractures with spacing of 13.5 m, 12 minor fractures with a spacing of 13 m and fracture aperture of 1.78 mm.

Conclusions

The workflow developed in this study through the use of FEA and semi-analytical method in characterizing fractures within the stimulated rock volume (SRV) is novel. FEA provides the characterization of fracture in terms of pressure drop, enhanced permeability and in situ stress change which are caused by hydraulic fracturing. The major and minor fractures aperture, numbers and spacing in between are computed through the use of semi-analytical method using inputs of the simulated enhanced permeability and the injected fracture fluid volume. Young’s modulus reduction leads to the increase the number of minor fractures for constant fracture apertures while decreases the effective permeability and the major fractures numbers. Decreasing the SRV dimensions by 10% of the original size resulted in the increase in the SRV effective permeability and decreases the pressure loss across the SRV. The hydraulic fractures effect the total in situ stress by increasing its values. Decreasing the size of the SRV dimensions leads to the increase in fracture apertures and the major fractures numbers while decreasing the minor fractures numbers to maintain the same decrease in pressure along the SRV length. For the case where the size of the SRV is calibrated to microseismic data from the field (Case 1), the analysis found the matching effective permeability to be 23.4 mD, fracture aperture to be 1.43 mm, major fracture number to be 5 with spacing of 13.1 m and the minor fracture number to be 12 with spacing of 14.9 m. For the case in which the SRV dimensions are reduced by 10% in each direction (Case 2), the matching effective permeability is 45.89 mD, the fracture aperture is 1.78 mm, the major fracture number is 4 with the spacing of 13.1 m and the minor fracture number is 12 with the spacing of 12.9 m. The variables tested in this study are applicable to improve the design of hydraulic fracturing in the Hoadley field or other formations and fields with similar geomechanical properties.