Introduction

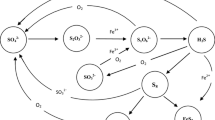
The injection of sulfate-containing seawater into an oil reservoir, for either maintaining the reservoir pressure or as an enhanced oil recovery (EOR) method, promotes the activity of sulfate-reducing bacteria and archaea near the injection wells, leading to the formation of hydrogen sulfide (H2S). The formation of hydrogen sulfide in originally sweet reservoirs is known as reservoir souring. The amount of hydrogen sulfide in the gas phase under test separator conditions is an indicator of the extent of souring. However, intermediate sulfur species with different valence states, between that of sulfate (+ 6) and sulfide (− 2), such as polythionates and polysulfides, have been detected in several produced water samples, due to oil production methods and subsequent chemical and microbial reactions, and phase partitioning (Putra and Hakiki 2019; Veshareh and Ayatollahi 2019; Miranda-Trevino 2013; Yu et al. 2006; Antonio et al. 2000; Witter and Jones 1998; Boulegue et al. 1981).

The level and types of sulfur species (i.e., sulfur speciation) are a function of temperature, pressure, pH, and composition. The intermediate sulfur species participate in various oxidation–reduction (redox) reactions. As conditions change within flowlines and unit operations, these species could degrade to corrosion causing and health and safety problematic compounds (Xu and Schoonen 1995; Xu et al. 2000; Druschel et al. 2003). The presence of reduced forms of sulfur impacts the bioavailability of toxic metals as complexation and precipitation of transition metals occur (Lewis 2010; Gramp et al. 2010; Witter and Jones 1998). The distribution of sulfur compounds is important to evaluate the effectiveness of souring mitigation options in either preventing the formation of sulfide or lowering the amount of sulfide already presents.

Microbial activity, thermochemical sulfate reduction, thermolysis of organosulfur compounds, and oxidative and reductive dissolution of metal sulfides impact sulfur production and speciation in the reservoir fluid. Previous studies of sulfur speciation have focused on sulfur chemistry in crude oils and asphaltenes (Pomerantz et al. 2013; Garcia et al. 2002). Sulfur is present in these organic phases in aliphatic chains, thiophenes, and sulfoxides. However, there is little study of sulfur speciation and chemical reactivity of inorganic sulfur compounds in reservoir fluids. The role of intermediate sulfur species in biological activity is well documented (e.g., Tang et al. 2009; Steudel 1996). However, there is a gap in knowledge in chemical reactivity of these inorganic sulfur species in seawater-flooded reservoirs. Therefore, identifying the reactivity and the partitioning behavior of these compounds is a critical step in developing souring control strategies.

The focus of this work is to investigate sulfur speciation as the reservoir fluid flows from injection to production in reservoirs undergoing seawater injection. As temperature and pressure change during production, sulfur species with different valence states are produced which impacts the pH of the environment, hydrogen sulfide concentration and distribution, and finally the extent of reservoir souring. A reactive model which includes both equilibrium and kinetic chemical reactions of sulfur species is developed to identify possible sulfur species of concern and predict relative sulfur speciation trend with changing temperature, pressure, and pH.

Methodology

Analysis of sulfur species reactivity

The chemical composition of a multi-component reacting system is controlled by the type of the chemical interactions between substances. The equilibrium and kinetically controlled reactions are combined to give a complete picture of the reaction pathways. The kinetic reactions are modeled based on the principle of conservation of mass. This results in a system of partial differential equations (PDEs). The equilibrium reactions are modeled based on equilibrium expression governed by mass action equilibrium equations resulting in a system of nonlinear algebraic equations (AEs) (Yeh and Tripathy 1989; Yeh et al. 2001; Steefel et al. 2005; Berk et al. 2015).

The plug flow reactor model is used for studying the chemical reactivity of sulfur species in a sample reservoir fluid under steady-state conditions. Assuming that the fluid is perfectly mixed in the radial direction and the composition of the reacting system is controlled by convection, the mole balance for each component in a plug flow reactor model, considering constant velocity of the fluid, is given by the following differential equation (Froment et al. 2009):

$$ u\frac{{{\text{d}}\left( {C_{i} } \right)}}{{{\text{d}}z}} = r_{i} $$
(1)

where u is the fluid velocity and ri is the rate of chemical reaction of species i.

Assuming that the sulfur reactions occur only in the aqueous phase, this equation leads to a system of ordinary differential equations for each species and can be solved numerically. The distance between injection and production is represented as a series of elements and within each element the temperature and pressure are varied. Concentration of each component is first calculated by solving the system of differential equations in the first element. However, not all reactions that could occur have published reaction rate equations; therefore, where there are reaction rate data gaps, it is assumed the reaction is governed by equilibrium. This enables one to include the desired compounds, present in the fluid, in the model. After the reaction rate equations are solved, the system of nonlinear algebraic equations obtained for equilibrium governed reactions is solved to get the final concentrations exiting the first element. The Gibbs reaction minimization method, summarized in the following section, is used for simulating the equilibrium reactions (Smith et al. 2005). The composition of the reacting system in the element is used as the input to the next element. The equilibrium and kinetic reactions are selected based on a comprehensive literature review followed by a screening study based on equilibrium analysis (Tables 1, 2).

Table 1 Equilibrium reactions of sulfur-containing compounds considered in this study (Moses et al. 1987; Machel 1987; Zhang and Millero 1991, 1993; Heinen and Lauwers 1996; Wilkin and Barnes 1996; Lin et al. 2004; Zhao et al. 2007; TengShui et al. 2009; Zhang and Jeffrey 2010; Miranda-Trevino et al. 2013)
Full size table
Table 2 Kinetic reactions of sulfur-containing compounds considered in this study at 25 °C (Machel 1987; Moses et al. 1987; Wilkin and Barnes 1996; Zhang and Millero 1991, 1993; Heinen and Lauwers 1996; Lin et al. 2004; Zhao et al. 2007; TengShui et al. 2009; Miranda-Trevino et al. 2013)
Full size table

Equilibrium analysis using Gibbs reaction minimization

When two or more independent reactions proceed simultaneously, the equilibrium mole fractions of (xi) of the species present are related to the reaction coordinate (ε) by (Smith et al. 2005):

$$ x_{i} = \frac{{n_{i0} + \sum\nolimits_{j} {\nu_{i,j} \varepsilon_{j} } }}{{n_{0} + \sum\nolimits_{j} {\nu_{j} \varepsilon_{j} } }} $$
(2)

where εj applies to each reaction and \( \nu_{i,j} \) designates the stoichiometric number of species i in reaction j. Summation over all species yields: \( \nu_{j} = \sum\nolimits_{i} {\nu_{i,j} } \). ni0 is the initial concentration of species i and n0 is the initial concentration of the reacting system.

The uniformity of temperature, pressure and chemical potential of each component throughout all the coexisting phases at equilibrium leads to:

$$ \sum\limits_{i} {\nu_{i} \mu_{i} } = 0 $$
(3)

According to the definition of the fugacity of a species in solution:

$$ \mu_{i} = \varGamma_{i} (T) + RT\ln \hat{f}_{i} $$
(4)

For pure species i in its standard state at the same temperature, this equation reduces to:

$$ G_{i}^{ \circ } = \varGamma_{i} (T) + RT\ln f_{i}^{ \circ } $$
(5)

The difference between these two equations gives:

$$ \mu_{i} - G_{i}^{ \circ } = RT\ln \frac{{\hat{f}_{i} }}{{f_{i}^{ \circ } }} $$
(6)

The equilibrium constant for a reaction can be evaluated as follows:

$$ \Delta G_{r}^{^\circ } = - \, RT\ln K $$
(7)

where the standard molal Gibbs free energy of the reaction (\( \Delta G_{r}^{^\circ } \)) is defined by Eq. (8):

$$ \Delta G_{r}^{^\circ } = \mathop \sum \limits_{i} \nu_{i,r} \Delta G_{i}^{^\circ } $$
(8)

where Pc is the stoichiometric coefficient and \( \Delta G_{i}^{^\circ } \) is the Gibbs free energy of formation for species i. Combining Eq. (3) with Eq. (4) and using the definition of equilibrium constant (Eq. 7) result in:

$$ \prod\limits_{i} {(\hat{f}_{i} /f_{i}^{ \circ } )^{{\nu_{i} }} } = K $$
(9)

For a reaction occurring in the liquid phase, the fugacity of a species in solution is related to its fugacity (fi) in the pure state at the temperature and pressure of the equilibrium mixture as follows:

$$ \hat{f}_{i} = \gamma_{i} x_{i} f_{i} $$
(10)

The activity coefficient (γi) is determined from Pitzer activity model (Sun et al. 2008). The fugacity ratio in Eq. (9) can now be expressed as:

$$ \frac{{\hat{f}_{i} }}{{f_{i}^{ \circ } }} = \frac{{\gamma_{i} x_{i} f_{i} }}{{f_{i}^{ \circ } }} = \gamma_{i} x_{i} \left( {\frac{{f_{i} }}{{f_{i}^{ \circ } }}} \right) $$
(11)

where this ratio is approximated as:

$$ \ln \frac{{f_{i} }}{{f_{i}^{ \circ } }} = \frac{{V_{i} (P - P^{ \circ } )}}{RT} $$
(12)

Finally, combining Eqs. (11) and (12) with Eq. (9) yields:

$$ \prod\limits_{i} {(x_{i} \gamma_{i} )^{{\nu_{i} }} } = K\exp \left[ {\frac{{(P^{ \circ } - P)}}{RT}\sum\limits_{i} {(\nu_{i} V_{i} )} } \right] $$
(13)

When there are two or more independent chemical reactions in a system, the equilibrium composition can be found by extension of the methods developed for single reactions. In this case, a separate equilibrium constant is evaluated for each reaction j:

$$ \prod\limits_{i} {(\hat{f}_{i} /f_{i}^{ \circ } )^{{\nu_{i,j} }} } = K_{j} $$
(14)

Heat capacity and critical data required for the calculation of equilibrium constants of each reaction are obtained from HSC Chemistry 9.0 database (Roine and Anttila 2006). Equilibrium constants are calculated based on the method suggested by Smith et al. (2005). In Eqs. (13) and (14), the mole fractions may be eliminated in favor of the equilibrium value of the reaction coordinate according to Eq. (2). This results in a system of nonlinear algebraic equations where the number of equations needed to be solved is equal to the number of reactions considered in the system.

It should be noted that the purpose of this study is not to mimic reservoir conditions as a function of distance, but rather to observe the effects of composition (and pH), temperature, and pressure, on the speciation of the products. The chemistry of sulfur species is studied for a sample seawater-flooded reservoir where hydrogen sulfide is generated microbially in a region close to the injection well. In order to reduce corrosion, oxygen scavengers, such as sulfite and bisulfite, are used in injection waters to react with dissolved oxygen and form sulfate (Eden et al. 1993). However, due to poor deaeration and inadequate scavenger injection, the presence of dissolved oxygen can occur (Maxwell 2006). At high-pressure conditions of downhole reservoirs, the solubility of oxygen in water is nearly proportional to its partial pressure. With the solubility of 3 mg oxygen/L seawater at atmospheric pressure, the solubility should be around 1400–1500 mg O2/L seawater at 30 MPa (Sunde et al. 1992). This provides the required amount of oxidant for the redox reactions to occur. The maximum amount of dissolved iron is directly related to iron sulfide solubility, and based on the approach followed by Verri and Sorbie (2017), it is approximately 0.1 mg/L for the current case study. Table 3 summarizes the initial conditions used in the model.

Table 3 Initial and reservoir conditions for studying H2S partitioning behavior (Stemler 2012)
Full size table

Results and discussion

Sulfur species reactivity and partitioning

The K-values for H2S partitioning between oil, water, and gas phases are first evaluated through equilibrium study and are then included in the reactivity analysis of sulfur species (Burger et al. 2013). The possibility of the formation of a separate solid phase of elemental sulfur is also considered where the amount of elemental sulfur formed in the reacting system is obtained from the reactive model and then based on the solubility of sulfur as a function of temperature and pressure, the amount of sulfur precipitated in the system is calculated (Smith et al. 2005).

In order to study sulfur speciation in the sample seawater-flooded oil reservoir, the initial pH of the solution at the injection point was varied: Case 1: initial pH = 5 (acidic), Case 2: initial pH = 7 (neutral), and Case 3: initial pH = 9 (basic). The pH of the solution, as the temperature and pressure change, was also tracked to examine the reactivity/speciation effect on the pH.

Figure 1 shows the results of sulfur speciation analysis as a function of temperature and pressure for initial pH of 5. It should be noted that in these figures, sulfur species is the summation of the concentration of sulfide, thiosalts, polysulfide ions, sulfate, and sulfite in the aqueous phase. Decreasing temperature and increasing pressure increase the solubility of sulfur in the aqueous phase. In theory, as the reservoir fluid transfers from reservoir to surface, the temperature and pressure drop and a fraction of total sulfur is converted to elemental sulfur. The solubility of the formed sulfur in the aqueous phase under reservoir conditions is low, and therefore, most of the sulfur forms as a separate solid phase and precipitates. An increase in temperature and a decrease in pressure increase the potential for elemental sulfur formation and, therefore, sulfur deposition. Sulfur solubility in the aqueous phase also decreases with a decrease in temperature. The combination of deposition of sulfur within the reservoir and increased sulfur solubility as the reservoir fluid flows toward topsides, meaning that the amount of elemental sulfur deposited from reservoir to wellhead decreases.

Fig. 1
figure 1

The effects of temperature and pressure on sulfur speciation, solid-phase formation, and H2S partitioning, aqueous-phase reactions, initial pH: 5, aT: 25 °C, bP: 1 MPa, cT: 75 °C, dP: 25 MPa (sulfur species is the total concentration of sulfate, sulfite, polysulfide ions, and thiosalts)

Full size image

The bubble point pressure of the reservoir fluid was calculated to be approximately 15 MPa. Above this pressure, no separate gas phase is evolved and the H2S partitions between oil and water (Fig. 1c, d). H2S solubility in the hydrocarbon-rich phase is higher than in the aqueous phase, and therefore, above the bubble point pressure, H2S is concentrated in the oil phase. When pressure is decreased and temperature is increased, a gas phase forms and H2S partial pressure increases in the gas phase (Fig. 1a, b). The amount of H2S in the gas phase from the model at test separator conditions is 487 ppm, while the H2S content of oil is 134 ppm and that of water phase is 4 ppm. Other sulfur species including thiosalts, polysulfide ions, sulfate, and sulfite constitute 90 ppm of the total sulfur in the aqueous phase. Elemental sulfur in the form of a separate solid phase is also formed at 965 mg/L. The pH of the solution varied slightly as the chemical reactions occurred. The initial pH increased from 5 to 5.2 as the pressure and temperature decreased from 35 MPa and 85 °C to 1 MPa and 15 °C.

Without considering the formation of other sulfur species (i.e., assuming that all the initial sulfate in the injected seawater is converted to H2S and partitions between phases), under test separator conditions, the gas phase would contain 1080 ppm, the oil phase contains 235 ppm, and water phase contains 7 ppm H2S. This large difference in the composition of produced fluid highlights the importance of studying sulfur speciation when investigating reservoir souring.

The impacts of temperature and pressure on sulfur speciation for Cases 2 and 3 are summarized in Figs. 2 and 3, respectively. Due to the dissociation of H2S to bisulfide at pH values near neutral, the amount of molecular H2S in the aqueous phase and, therefore, the amount in oil and gas phases in equilibrium decreases.

Fig. 2
figure 2

The effects of temperature and pressure on sulfur speciation, solid-phase formation, and H2S partitioning, aqueous-phase reactions, initial pH: 7, aT: 25 °C, bP: 1 MPa, cT: 75 °C, dP 25 MPa (sulfur species is the total concentration of sulfate, sulfite, polysulfide ions, and thiosalts)

Full size image
Fig. 3
figure 3

The effects of temperature and pressure on sulfur speciation, solid-phase formation, and H2S partitioning, aqueous-phase reactions, initial pH: 9, aT: 25 °C, bP: 1 MPa, cT: 75 °C, dP: 25 MPa (sulfur species is the total concentration of sulfate, sulfite, polysulfide ions, and thiosalts)

Full size image

As the reservoir fluid flows from reservoir to the surface, and the temperature and pressure decrease, elemental sulfur forms. As discussed before, the solubility of the elemental sulfur in the aqueous phase decreases with a decrease in temperature and an increase in pressure and therefore, forms as a separate solid phase and precipitates. However, sulfur of oxidation state zero (S°) has low chemical stability at high pH values and therefore, less elemental sulfur is formed compared to acidic conditions.

At high pH values, the amount of H2S in the aqueous phase decreases as it dissociates to sulfide and bisulfide resulting in an overall decrease in the H2S content of oil and gas phases. The presence of sulfur species with different valence states influences the amount of molecular H2S in the aqueous phase and, consequently, the amount formed in other phases in equilibrium. At pH values above 7, H2S dissociates to sulfide which could be oxidized to thiosulfate (Chen and Morris 1972) initiating the formation of tetrathionate, polysulfide ions, and elemental sulfur. At these conditions, thiosulfate is converted to sulfide and sulfate (Lin et al. 2004). The pH of the reacting system decreases from 9 to 8.7 as the pressure and temperature change from 35 MPa and 85 °C to 1 MPa and 15 °C.

The amount of H2S in the gas phase from the model at test separator conditions is 7 ppm, while the H2S content of oil is 2 ppm and that of water phase is 0.06 ppm. Other sulfur species including thiosalts, polysulfide ions, sulfate, and sulfite make up 65 ppm of the total sulfur aqueous phase. Elemental sulfur in the form of a separate solid phase is also formed (845 mg/L).

When the initial pH of the solution is above neutral conditions (case 3), less polysulfide ions form in the solution, while the amount of sulfate and thiosalts, especially thiosulfate and pentathionate, increase with the pH. H2S dissociates to sulfide and bisulfide, and therefore, the amount of molecular H2S in the aqueous phase and that in the oil and gas phases decreases. Again, in this case, one might estimate 0.5 ppm H2S in the aqueous phase, 22.5 ppm H2S in the gas phase, and 13.4 ppm H2S in the oil phase with ignoring sulfur speciation which leads to over prediction of H2S in the reservoir fluid.

Figure 4 illustrates sulfur speciation as a function of pH of the environment. Sulfur speciation is significantly influenced by the pH of the solution. Increasing the pH from acidic to basic is accompanied with the formation of polysulfides. At low pH values, H2S exists in the molecular form and partitions between oil, water, and gas phases below bubble point pressure. As pH increases, H2S dissociates to sulfide and bisulfide resulting in the decrease in the H2S content of all phases at equilibrium.

Fig. 4
figure 4

The effect of pH on sulfur speciation, solid-phase formation, and H2S partitioning, aqueous-phase reactions, aT: 25 °C, P: 1 MPa, bT: 75 °C, P: 25 MPa (sulfur species is the total concentration of sulfate, sulfite, polysulfide ions, and thiosalts)

Full size image

Table 4 summarizes the results of sulfur speciation for the three cases. These results are compared to the base case study where no sulfur speciation is considered and all the sulfur is in the form of H2S.

Table 4 Comparison of the results of sulfur speciation for three cases at T: 15 °C, P: 1 MPa
Full size table

Model evaluation

The results of the sulfur speciation obtained in this study were compared with experimental data for a sample produced water generated in offshore oil production (Witter and Jones 1998). Sulfide, polysulfide ions, thiosulfate, sulfite, and sulfate were measured in the produced water sample. Elemental sulfur and polythionates were not considered. However, it was indicated that elemental sulfur is present in the produced water sample in low concentrations (Witter and Jones 1998). More than 39% of the measured inorganic sulfur compounds were sulfide (HS− and S2−) making it the second most abundant species after sulfate (56% of the total inorganic sulfur compounds). Polysulfide ions and thiosulfate formed 3% and 2% of the measured sulfur species, respectively. Sulfite accounted for less than 1% of sulfur in the produced water.

According to the proposed model, at atmospheric temperature and pressure and under basic conditions (similar to the conditions in the study of Witter and Jones 1998), sulfate and thiosalts constitute 58% and 23% of the total sulfur, respectively. Pentathionate accounted for 17% of the total thiosalts. Thiosulfate, trithionate, and tetrathionate constitute 1.8%, 1.5%, and 2.7% of the total sulfur, respectively. Approximately, 4% of the total sulfur was polysulfide ions (S22−, S32−, S42−, and S52−). At high pH values, hydrogen sulfide dissociates to sulfide and bisulfide making up approximately 12% of the total sulfur in the reacting system. Elemental sulfur deposition was 880 mg/L or less than 3% of the total sulfur in the aqueous phase.

Table 5 summarizes the results of reactivity analysis in this study compared to the experimental data by Witter and Jones for a sample produced water. There is a good agreement between the model predictions and the experimental data. However, no experimental data on intermediate sulfur species such as polythionates were reported. This could partially explain the difference in the concentration of sulfide and polysulfides in the proposed model and the experimental data. Furthermore, the values of first and second dissociation constants of H2S in water were obtained from various references (Sun et al. 2008). There is no consistent data for these values in the literature and this could result in some error in the calculation of the final composition of the produced fluid.

Table 5 Sulfur speciation at 25 °C and 101 kPa, pH = 9
Full size table

This study contributes toward predicting sulfur chemistry in soured reservoirs as it examined the reactivity, partitioning behavior and therefore, relative impact of different sulfur species on H2S partitioning behavior and finally, on reservoir souring, and therefore, enables one estimating the quality of the produced fluid as a result of seawater injection for enhancing oil recovery.

Conclusions

A new approach was followed in this study for studying sulfur chemistry in reservoirs undergoing seawater injection in an attempt to fill the gap in addressing reservoir souring-related issues in offshore operations. Most souring models and management plans do not include sulfur speciation and consider only microbially conversion of the initial sulfate in the injected seawater to H2S. This results in the potential for over prediction of H2S in the reservoir fluids. For instance in this study, the gas phase under test separator conditions on the surface would contain 1080 ppm H2S, the oil phase contains 235 ppm H2S, and water phase contains 7 ppm H2S without including sulfur chemistry. At low pH values, sulfate, polysulfide ions, and hydrogen sulfide are dominant in the solution. Less than 10% of the total sulfur is formed as thiosalts, predominantly as thiosulfate and pentathionate. Part of the total sulfur is present as elemental sulfur. The solubility of the formed sulfur in the aqueous phase, in the range of temperature and pressure considered in this study, is not high, and therefore, it precipitates as the fluid moves to top surface such that approximately 960 mg/L solid sulfur is deposited at the producer (15 MPa, 65 °C). Using the developed reactive model for predicting the partitioning behavior of sulfur species, under test separator conditions, a gas phase containing 487 ppm H2S forms, while the H2S content of oil and water phases in equilibrium is 134 ppm and 4 ppm, respectively. When the pH of the solution is above neutral, most of the total sulfur is found as sulfate and thiosalts. Hydrogen sulfide dissociates to sulfide and bisulfide and less than 10% polysulfide ions forms. The amount of sulfur deposited as elemental sulfur is slightly decreased from 965 mg/L at low pH values to less than 844 mg/L at higher pH values. In addition, at high pH values, the amount of molecular H2S which partitions between phases is decreased significantly. The sulfur reactivity results in the formation of 7 ppm H2S in the gas phase, 2 ppm in the oil phase, and 0.06 ppm in the water phase.

If sulfur speciation is not considered in determining the extent of reservoir souring, souring mitigation methods could lead to over-treating a reservoir. It also impacts the effectiveness of the produced water treatment systems. Considering the limited space for equipment to treat or mitigate souring on offshore platforms, these issues represent a cost and logistical problem. Current reservoir models oversimplify the complex sulfur chemistry, and developing effective souring control method requires the complete picture. Therefore, the major contribution of this study is identifying the key chemical compounds, reaction schemes, and developing a methodology to incorporate into a more comprehensive reservoir simulator, to model transport and transformation in reservoirs soured via seawater injection.