Introduction

Since the successful application in the USA in 1947, hydraulic fracturing has already become the most effective means of increasing production and transformation in low-permeability oil and gas reservoirs (Haddad and Sepehrnoori 2016; Kumar et al. 2017), which occupies an increasingly important position in oil and gas reservoir transformation(Wang et al. 2017a, b; Luo et al. 2019). According to statistics, currently 60% of global oil and gas wells need hydraulic fracturing (Luo et al. 2018). However, the existing common fracturing technology is generally of shortcomings such as residue damage, sand plugging and equipment wearing (Liu et al. 2014, 2016; Hu et al. 2019). To solve these problems, a new type of fracturing technology, the self-propping fracturing technology (called SPFT for short) is currently under development (Yixin 2017). This technology injects a self-propping fracturing liquid system composed of a self-propping fracturing liquid (called SPFL for short) and a channel fracturing fluid (called CFL for short) into the formation. Under the formation temperature, the SPFL undergoes a phase transition from liquid phase to self-propping solid phase (called SPSP for short), replacing common proppants such as ceramic particles and quartz sand to prop hydraulic fractures.

During the construction of SPFT, to achieve a higher conductivity and form an effective support, the key is to form a good distribution pattern of the self-propping fracturing liquid, and the distribution of the self-propping fracturing liquid determines the distribution of the SPSP formed by the phase transition. The flow distribution of the SPFL system is included in the follow-up study of liquid–liquid two-phase flow interface. To study the influence of leak-off rate, surface tension and injection velocity on the two-phase flow pattern, effective distance and filling ratio of the SPFL system is of great significance to improve the hydraulic fracture conductivity and increase the effective length of the propped fracture.

At present, most two-phase flow researches focus on the two-phase velocity measurement and two-phase distribution (Chinaud et al. 2017). The two-phase distribution is greatly affected by the flow velocity and physical parameters of the fluid, while physical experiments can show the two-phase flow phenomenon more intuitively, and are therefore favored by most researchers. Under the control of two-phase surface tension and viscous force, the formation mechanism of discrete phases in two-phase flow can be divided into three modes: squeezing, dripping and jetting (Yeom and Lee 2011). Using water as the continuous phase and oil as the discrete phase, Zhao et al. (2006) observed the oil–water two-phase flow pattern in a planar fracture with a diameter of 400 μm. They found that there were six basic flow patterns of the oil–water two-phase flow in the fracture, namely slug flow, droplet flow, continuous droplet flow, parallel flow, undulatory parallel flow and tumbling flow. Grabenstein et al. (2017) established the functional relationship between flow pattern and pressure drop by conducting two-phase flow experiments in corrugated plates. The experiments show that regular flow pattern is formed between the two corrugated plates, and each specific flow pattern has a strong correlation with pressure drop. In terms of two-phase flow in hydraulic fractures, Arshadi et al. (2017) used oil and brine as experimental fluids, split a natural rock into two halves, and filled in the section with proppants of different thicknesses representing hydraulic fractures propped by proppants. Subsequently, oil and brine were injected to observe the saturation distribution of the two-phase fluid within the fractures. In Maziar Arshadi’s experiment, due to the small size of the physical model, it is difficult to observe the impact of fluid leak-off on oil and brine two-phase flow.

Using experimental methods to observe the flow pattern of fluids needs advanced experimental instruments and equipment that require a great amount of time and economic costs. However, using mathematical methods to perform numerical simulations can, to some extent, reduce research time, equipment and personnel inputs. Therefore, a numerical simulation method is widely used in research on fluid flow, mixing and flow patterns. The common numerical simulation methods include level set (Coquerelle and Glockner 2016; Rodríguez 2017; Anumolu and Trujillo 2018), VOF (volume of fluid) (Cerroni et al. 2017; Pozzetti and Peters 2018) and LBM (lattice Boltzmann method) (Gong et al. 2016; Hassine et al. 2017; Amirshaghaghi et al. 2018), each of which has advantages and disadvantages, as well as corresponding specific conditions to use (Prajapati 2014). Among them, the VOF method only needs to introduce a new scalar function to track the fluid interface when calculating the two-phase flow. The two-phase fluids share a momentum equation, the calculation speed is faster and fewer computational resources are consumed, and it is, therefore, suitable for large-scale engineering calculations (Nguyen and Park 2017). After decades of development since the birth of the VOF method, scholars have been committed to improving it, and today a large number of VOF-based phase interface tracking methods have been developed (Owkes and Desjardins 2014; Sharma et al. 2017; Wang et al. 2017a, b, 2018).

Based on the Navier–Stokes equations, a two-phase flow model for the SPFL system considering fracturing fluid leak-off was established. The VOF method was used to track the interface, and the numerical simulation results were compared with the physical experiments’ results to verify the mathematical model’s accuracy. The flow pattern, effective distance and filling ratio of the SPFL system under different leak-off rates, surface tensions and injection velocities were simulated.

Model and methods

Physical model

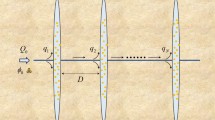
As shown in the physical model in Fig. 1, inject the self-propping fracturing liquid and the CFL, both of which are immiscible, from the inlet, and set the boundary condition at the inlet as velocity inlet and the outlet as pressure outlet. Formation rock is a kind of porous medium. A part of the SPFL and CFL in the hydraulic fracture will leak off into the formation along the direction perpendicular to the wall of hydraulic fracture, resulting in that the total volume of SPFL system in hydraulic fractures is less than the volume injected. In fact, in the fracturing construction, the hydraulic fracture width is a few millimeters, while the hydraulic fracture height and length can reach tens of meters or even hundreds of meters. Therefore, the fluid velocity, pressure and volume fraction will not change significantly along the direction perpendicular to the wall of hydraulic fracture. In order to mitigate the workload of computers and improve the computational efficiency, a two-dimensional model was used for calculation, and the variation of field variables along the direction perpendicular to the wall of hydraulic fracture is negligible.

Fig. 1
figure 1

Physical model

Full size image

Governing equations

The physical flow process of the SPFL system is a representative of the liquid–liquid two-phase flow. In order to track the two-phase flow interface between the self-propping fracturing liquid and the CFL, the VOF method was used to establish a mathematical model for liquid–liquid two-phase flow interface distribution considering the fluid leak-off of the fracturing fluid along the wall of hydraulic fracture based on the Navier–Stokes equations. The mathematical model consists of a continuity equation and a momentum equation.

Neglecting the compressibility of the SPFL system, the fluid volume change rate is zero, and the volume change rate of continuous medium can be characterized by the velocity divergence. Considering the fluid leak-off along the wall of hydraulic fracture, the continuity equation is:

$$\nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} + \frac{{2v_{l} }}{w} = 0$$
(1)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}\) is the fluid particle velocity in the flow field; v1 is the fluid leak-off rate along the wall of hydraulic fracture; and w is the width of the fracture.

In the entire computational domain, two-phase fluids share one momentum equation, expressed as:

$$\rho \left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{V} }}{\partial t} + \nabla \cdot \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} } \right)} \right) = \rho g + f_{it} + \nabla \cdot \sigma$$
(2)

where ρ is the fluid density; g is the gravitational acceleration; fit is the pressure gradient produced by the surface tension; and σ is the full stress of the flow field.

fit may be calculated using the continuous surface tension model (Brackbill et al. 1992), which successfully applies the influence of surface tension on the two-phase flow numerical simulation, and treats the surface tension as a source item of the momentum equation. In the continuous surface tension model, the mean curvature of the fluid interface κ is calculated using the normal direction vector \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}\) at the fluid interface:

$$\kappa { = }\nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}$$
(3)

The normal direction vector \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}\) of the fluid interface is calculated by the gradient of the fluid volume fraction F at the fluid interface:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} = \frac{\nabla F}{{\left| {\nabla F} \right|}}$$
(4)

In the continuous interface tension model, there is a pressure gradient at the fluid interface due to surface tension. This pressure gradient can be added as a volume force item to the source interface of the momentum equation as follows:

$$f_{it} = - \delta \kappa \nabla F$$
(5)

where δ is the surface tension coefficient.

For incompressible flows, the full stress of the flow field σ can be expressed as:

$$\sigma = \tau - P$$
(6)

where τ is the viscous force and P is the pressure.

The linear constitutive relation between the viscous force τ and the strain rate tensor D:

$$\tau = 2\mu D = \mu \left[ {\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} + \left( {\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} } \right)^{T} } \right]$$
(7)

where μ is the viscosity.

The VOF method is used for interface tracking. VOF describes the change of phase interface by tracking the volume fraction of grid cells occupied by a certain phase fluid. It assumes a fluid volume fraction function F in each divided grid to calculate and solve the control equations so as to achieve the purpose of tracking the phase interface in the flow process (Brackbill et al. 1992; Gao et al. 2003). When the scalar function F is 0, it means that the grid contains only one phase. When F is 1, it means that the grid contains only the other phase. When F is between 0 and 1, it means that there are two kinds of fluids inside the grid, that is, phase interface exists (Meier et al. 2002). The VOF expression is:

$$\frac{\partial F}{\partial t} + \nabla \cdot \left( {F\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} } \right) = 0$$
(8)

The viscosity μ and density ρ in Eqs. (2) and (7) are determined by the volume fraction F in each control volume. In the two-phase flow system, the viscosity μ and density ρ are calculated as follows:

$$\begin{aligned} \rho & = F\rho_{0} + \left( {1 - F} \right)\rho_{1} \\ \mu & = F\mu_{0} + \left( {1 - F} \right)\mu_{1} \\ \end{aligned}$$
(9)

where ρ0, ρ1, μ0 and μ1 are the density and viscosity of the two-phase fluids, respectively.

Boundary and initial condition

When using the SPFT, a common high-viscosity fracturing fluid is injected first, and the formation is forced open to form an artificial hydraulic fracture. Afterward, the SPFL system is injected with the inflow boundary as the velocity boundary and the outflow boundary as the pressure boundary. Given the volume fraction of the self-propping fracturing liquid at the inlet is F0, the boundary condition is:

$$\left\{ {\begin{array}{*{20}l} {\left. P \right|_{x = L} = P_{0} } \hfill & {} \hfill \\ {\left. u \right|_{x = 0} = u_{0} } \hfill & {\left. v \right|_{x = 0} = v_{0} } \hfill \\ {\left. F \right|_{T = 0} = 0} \hfill & {\left. F \right|_{x = 0} = F_{0} } \hfill \\ \end{array} } \right.$$
(10)

where T = 0 is to the moment of starting to inject the SPFL system; x = L is the coordinates of the outlet; P0 is the pressure at the outlet, and \(v_{0}\) are the velocities in x and y directions at the inlet; F0 is the volume fraction of the self-propping fracturing liquid at the inlet.

Solution method

The finite element method is used to discretize the equation. The numerical expression of the continuity equation is as follows:

$$\left[ {\iint\limits_{{\varOmega^{e} }} {\varPhi \frac{{\partial \varPhi^{T} }}{\partial x}{\text{d}}x{\text{d}}y}} \right]u_{I}^{e} + \left[ {\iint\limits_{{\varOmega^{e} }} {\varPhi \frac{{\partial \varPhi^{T} }}{\partial y}{\text{d}}x{\text{d}}y}} \right]v_{I}^{e} + \left[ {\iint\limits_{{\varOmega^{e} }} {2\varPhi v_{lm} }} \right] = 0$$
(11)

where Φ is the interpolation function and \(\varOmega^{e}\) is the element integral region.

The numerical expression of the momentum equation in X and Y directions is similar. The numerical expression of the momentum equation is as follows:

$$\begin{aligned} & \left[ {2\mu \iint\limits_{{\varOmega^{e} }} {\frac{\partial \varPhi }{\partial x}\frac{{\partial \varPhi^{T} }}{\partial x}{\text{d}}x{\text{d}}y + \mu \iint\limits_{{\varOmega^{e} }} {\frac{\partial \varPhi }{\partial y}\frac{{\partial \varPhi^{T} }}{\partial y}{\text{d}}x{\text{d}}y}}} \right]u_{I}^{e}\\&\quad + \left[ {\mu \iint\limits_{{\varOmega^{e} }} {\frac{\partial \varPhi }{\partial x}\frac{{\partial \varPhi^{T} }}{\partial x}{\text{d}}x{\text{d}}y}} \right]v_{I}^{e} - \left[ {\iint\limits_{{\varOmega^{e} }} {\frac{\partial \varPhi }{\partial x}\varPhi^{T} }{\text{d}}x{\text{d}}y} \right]\;p_{I}^{e}\\&\quad + \iint\limits_{{\varOmega^{e} }} {\rho f}{\text{d}}x{\text{d}}y = - \int\limits_{{\varGamma^{e} }} {\varPhi \varPhi^{T} p_{I}^{e} \cos \theta_{x} d\varGamma } \\ \end{aligned}$$
(12)

The numerical expression of the VOF equation is as follows:

$$\iint\limits_{{\varOmega^{e} }} {\varPhi \varPhi }^{T} \frac{{\partial \alpha_{I}^{e} }}{\partial t}{\text{d}}x{\text{d}}y + \iint\limits_{{\varOmega^{e} }} {\varPhi \left[ {u,v} \right]}\left[ {\frac{\partial \varPhi }{\partial x},\frac{\partial \varPhi }{\partial y}} \right]^{T} \alpha_{I}^{e} {\text{d}}x{\text{d}}y = 0$$
(13)

Results and discussion

Model verification

In order to verify the reliability of the mathematical model, a physical simulation experiment was performed using a physical simulation device for the flow of the SPFL system (see Fig. 2). The device uses nitrogen gas to displace the self-propping fracturing liquid and CFL to enter the visualized planar fracture. A camera is used to film the experimental phenomena. The visualized planar fracture’s size is 1 m × 2 m. There is an injection pipe on the left side of the visualized planar fracture to simulate the borehole. For the SPFL system on the right side of the visualized planar fracture, the injection flow can be calculated by measuring the outflow fluid volume.

Fig. 2
figure 2

Physical simulation device for the flow of the SPFL system

Full size image

The experimental parameters are shown in Table 1.

Table 1 Simulation parameters
Full size table

Physical simulation experiments are performed using the experimental device shown in Fig. 2, and the parameters are shown in Table 1. The results are shown in Fig. 3. According to the data shown in Table 1, the mathematical model established herein was used for numerical simulation experiments. The simulation results are shown in Fig. 4.

Fig. 3
figure 3

Results of physical simulation experiments

Full size image
Fig. 4
figure 4

Results of numerical simulation experiments

Full size image

As shown in Figs. 3 and 4, under the control of surface tension and two-phase viscosity, the SPFL is distributed in the hydraulic fracture in the form of circular and strip-like discontinuous phase, while the CFL is a continuous phase. The similarity between the numerical simulation results and the physical experiments indicates that the mathematical model can reflect the flow pattern of the SPFL system to some extent.

Numerical examples

Leak-off

The physical model shown in Fig. 2 is far smaller than the hydraulic fracture in the process of actual fracturing, so it is a simplified version of the actual one based on the similarity criterion, and it cannot thoroughly reflect the process of fracturing. For example, as the physical model is relatively small, it will not able be to completely reflect the influence of leak-off and in the process of actual fracturing, due to the leak-off, the self-propping fracturing liquid might have leaked off in the formation before reaching the front edge of the fracture. As a result, on the basis of simulated parameters given in Table 1, the size of the model is designed as 100 m × 40 m, the fluid leak-off rate is changed to 0 m/s, 0.005 m/s, 0.01 m/s and 0.02 m/s, respectively, and other parameters will remain unchanged, in order to study the influence of fluid leak-off rate on interface distribution of the self-propping fracturing liquid. Calculation results are shown in Fig. 5.

Fig. 5
figure 5

Volume fractions of the self-propping fracturing liquid at different fluid leak-off rates

Full size image

Equation (2) considered the effects of gravity, so the self-propping fracturing fluid with larger density is apt to gather toward the bottom of the fracture.

When the fluid leak-off rate is high, the self-propping fracturing liquid cannot flow to the front edge of the fracture, and with the gradual increase in the rate, the volume of self-propping fracturing liquid leaking off to the formation along the direction perpendicular to the wall of hydraulic fracture may become larger, while the volume of self-propping fracturing liquid in the fracture may be smaller, thus lowering the movement distance thereof. When the fluid leak-off rate is 0 m/s, the self-propping fracturing liquid may institute in the entire fracture. When the rate rises to 0.005 m/s, the front edge of the fluid can flow to the farthest end in the fracture and due to the effect of gravity, the velocity of movement of the self-propping fracturing liquid at the bottom of the fracture may be faster and can be easier to reach the far end, but no self-propping fracturing liquid exists at the top right corner of the fracture.

Effective distance and filling ratios are introduced for the representation of the movement distance and distribution characteristics of the self-propping fracturing liquid. Specifically, the effective distance refers to the farthest distance that the front edge of the self-propping fracturing liquid can reach and the filling ratio refers to the percentage of the self-propping fracturing liquid’s filling area to the total area of fracture, as shown in Figs. 6 and 7.

Fig. 6
figure 6

Effective distances at different fluid leak-off rates

Full size image
Fig. 7
figure 7

Filling ratios at different fluid leak-off rates

Full size image

The fluid leak-off rate has a great impact on both effective distance and filling ratio. When the fluid leak-off rate increases from 0 to 0.015 m/s, the effective distance will drop from 100 to 50 m and the filling ratio will decrease from 78 to 30%. In the process of fracturing, it is vital to provide sufficient effective length of the propped fracture and enough fracture conductivity, and measures to reduce fluid leak-off rates shall be taken, such as adding the filtrate reducer and increasing the injection volume, which enables to increase the effective distance and the filling ratio to some extent.

Surface tension

Surface tension can be interpreted as the shrinkage force imposed on liquid interface per unit length. Microscopically, molecules on the interface bear different forces from those in the phase. Specifically, molecules in the phase bear symmetrical and balanced force, with the resultant force equaling to zero; on the contrary, molecules on the surface or interface bear different attraction forces from upper and lower layers, as a result of which, the resultant force is not zero, but in general points to the inside of the fluid vertically. Due to the existence of surface tension, discrete phases are apt to shrink as clusters. Therefore, the surface tension exerts a great influence on the interface distribution of the SPFL system. As shown in Table 1, the size of the physical model is designed as 100 m × 40 m, and surface tension is changed to 3 mN/m, 5 mN/m, 7 mN/m and 9 mN/m, respectively, in order to study the influence of surface tension on interface distribution. The calculation results are shown in Fig. 8.

Fig. 8
figure 8

Volume fractions of the self-propping fracturing liquid at different surface tensions

Full size image

Surface tension determines the intensity of shrinkage of the SPFL as discrete phases, that is, the larger the surface tension is, the easier the SPFL shrinks. According to the simulation results in Fig. 8, the larger the surface tension is, the larger the area of a single droplet formed by the SPFL, and the clearer the interface between the SPFL and the CFL is; on the contrary, the smaller the surface tension is, the blurrier the interface between them is.

The effect of the surface tension on the effective distance or the filling ratio is subtle, and the effective distance is up to 100 m, while the filling ratio is within 63%–68% (see Figs. 9 and 10). However, as for the tendency of change, with the increase in the surface tension, the filling ratio becomes smaller.

Fig. 9
figure 9

Effective distances at different surface tensions

Full size image
Fig. 10
figure 10

Filling ratios at different surface tensions

Full size image

Injection velocity

The injection velocity, to some extent, affects the total leak-off volume. When the total injection volumes are the same, the faster the injection velocity is, the less the total leak-off volume is, and vice versa. Therefore, the injection velocity is significantly influential to the effective distance and the filling ratio. The parameters shown in Table 1 indicate that the size of the physical model is designed as 100 m × 40 m, injection velocity is changed to 0.1 m/s, 0.15 m/s, 0.2 m/s and 0.25 m/s, respectively, and other parameters will remain unchanged, in order to study the influence of injection velocities on the interface distribution of the SPFL. Calculation results are shown in Fig. 11.

Fig. 11
figure 11

Volume fractions of the SPFL at different injection velocities

Full size image

When the total injection volumes are the same, the larger the injection velocity is, the shorter the time required for injection is and the less the total leak-off volume is. Therefore, the larger the volume of SPFL in the fracture is, the farther the movement distance is. When the injection velocity is 0.1 m/s, the time required for injection is the longest, and the effect of gravity on the SPFL is relatively obvious. Besides, the X-direction velocity of movement of the SPFL at the fracture bottom is far higher than that at the top, and non-uniform advancement velocities appear at the front edge thereof. With the increase in the injection velocity, the total leak-off volume is less, the effect of gravity becomes less obvious, and the front edge of SPFL is apt to advance uniformly.

As the effective distance refers to the distance reached by the foremost end of the SPFL and under the effect of gravity, when the injection velocity is relatively small, the SPFL is apt to gather at the fracture bottom, making the X-direction velocity of the fluid at the bottom larger. As a result, when the injection velocity is 0.1 m/s or 0.15 m/s, the difference of effective distances is subtle. At both injection velocities, the most significant difference is the X-direction velocity of movement of the SPFL at the top of the fracture, and the velocity of movement of the fluid at the top in Fig. 11b is obviously larger than that in Fig. 11a. Therefore, the filling ratios are different. In general, the larger the injection velocity is, the larger the effective distance and the filling ratio are (see Figs. 12 and 13).

Fig. 12
figure 12

Effective distances at different injection velocities

Full size image
Fig. 13
figure 13

Filling ratios at different injection velocities

Full size image

Conclusion

The flow of the SPFL system is a kind of liquid–liquid two-phase flow. However, different from common liquid–liquid two-phase flow, it is necessary to consider the leak-off from the wall of hydraulic fracture to the formation in the process of self-propping fracturing.

The mathematical model for the flow of SPFL system established in this paper has considered the influence from surface tension, gravity and leak-off, to some extent, reflected the actual physical process of two-phase flow of self-propping fracturing.

The numerical simulation results and physical experiment results are highly similar, and the mathematical model established in this paper can mirror the flow pattern of the self-propping fracturing system. Flow patterns, effective distances and filling ratios at different fluid leak-off rates, surface tensions and injection velocities have been calculated, and according to simulation results, leak-off, surface tension and injection velocity have a great impact on the flow pattern, effective distance and filling ratio of the SPFL system.