Introduction

The first stage in the petroleum industry to access a hydrocarbon reservoir is the drilling operation. During drilling operation, drilling fluid is the most crucial and important components, which is usually called drilling mud. Among all types of drilling fluid (water-based, oil-based, and synthetic-based), water-based drilling fluids are the most widely used fluids in the drilling industry in comparison with the other types that is due to their higher cost, environmental issues, disposal problems, and health and safety issues (Mahmoud et al. 2016). Drilling fluids are responsible to carry out many different functions during the drilling process as controlling the formation hydrostatic pressure, preventing collapse of wellbore surface, transferring cuttings to the surface, suspending cuttings and additives, preventing formation damage by forming good mudcake on the wellbore surface, lubricating and cooling the bit and drilling string, and so on. Therefore, these fluids should be designed and manufactured well in such a specific characterization in order to handle the above functions. To modify or enhance a specific function or property, some additives are also added to the drilling fluid. The success of a drilling operation is closely related to the design and performance of the drilling fluid (Mahmoud et al. 2016). In order to minimize the encountered problems and to have low-cost drilling, the functions of drilling fluid must be optimized by improving the drilling fluid properties (Salih and Bilgesu 2017). Most of the problems encountered during the drilling operation such as stuck pipe, high torque and drag, surge and swab pressures, bit balling, shale swelling, and loss circulation are because of improper drilling fluid design (Bourgoyne et al. 1986) that are directly or indirectly related to hydraulic, rheological, and filtration properties of the drilling fluid (Salih and Bilgesu 2017). Therefore, one of the integral and essential tasks is to monitor and control the drilling fluid properties (Vryzas et al. 2018) that should be scheduled in the predefined drilling program. The effect of additives and also human must be added to the usual problems that are encountered during the drilling process that affect the drilling fluid properties.

Among the mentioned problems, one of the most crucial one is drilling fluid loss into the formation. Mitigating and controlling the fluid loss is essential to reduce both the formation damage and the cost of drilling fluid. So many fluid loss agents are added to the drilling fluid as fluid loss additives (Vryzas et al. 2016). The function of these additives is to make a filter cake on the wellbore surface in order to mitigate or prevent fluid loss into the formation, which is usually called mudcake (Barry et al. 2015). For this purpose, fluid loss agents must be optimized to have a homogeneous, thin, and low permeable mudcake. Whether the mudcake is thick or highly permeable, it would increase the probability of pipe sticking or the filtration volume of the drilling fluid, respectively.

By the arrival of nanotechnology, the special characteristics of nanoparticles have made them a potential additives in several fields of the sciences in order to mitigate, minimize, or solve the encountered problems, and moreover to improve the characteristic of a material or a process. Over the time, nanoparticles have also got involved in various fields of oil and gas industry. Recently, various nanoparticles are utilized by many researchers to improve the filtration properties of the water-based drilling fluids while maintaining the other drilling fluid properties optimal or to improve them.

The effect of silica (SiO2) (Mahmoud et al. 2016, 2018; Salih and Bilgesu 2017; Parizad et al. 2018; Smith et al. 2018; Salih et al. 2016; Vryzas et al. 2015; Yusof and Hanafi 2015), ferric oxide (Fe2O3) (Mahmoud et al. 2016, 2017, 2018; Vryzas et al. 2015; Jung et al. 2011; Shakib et al. 2016), aluminum oxide (Al2O3) (Salih and Bilgesu 2017; Smith et al. 2018; Shakib et al. 2016), titanium oxide (TiO2) (Salih and Bilgesu 2017; Shakib et al. 2016), copper oxide (CuO) (Shakib et al. 2016), stannic oxide (SnO2) (Parizad and Shahbazi 2016), ferrosoferric oxide (Fe3O4) (Vryzas et al. 2016, 2018), and clay minerals (Shakib et al. 2016; Needaa et al. 2016) nanoparticles on filtration properties of water-based drilling fluid is investigated. The other types of nanoparticles as multi-walled carbon nanotube (MWCNT) (Ismail et al. 2014, 2016), iron oxide/clay hybrid (ICH) (Barry et al. 2015), aluminosilicate/clay hybrid (ASCH) (Barry et al. 2015), titanium oxide/polyacrylamide nanocomposite (Sadeghalvaad and Sabbaghi 2015), clay/silica nanocomposite (Cheraghian et al. 2018), nano-sized layered magnesium aluminum silicate (MAS) (Wang et al. 2018) are also utilized for this purpose. Also, the effects of nanoparticles along with the polymers, surfactants, and polymer–surfactant are dealt with in some other works (Fakoya and Shah 2018; Srivatsa and Ziaja 2011; Ahmad et al. 2017). The above investigations have showed that the addition of nanoparticles could improve the filtration properties of drilling fluid (Mahmoud et al. 2016, 2017, 2018; Salih and Bilgesu 2017; Vryzas et al. 2015, 2016, 2018; Barry et al. 2015; Parizad et al. 2018; Smith et al. 2018; Salih et al. 2016; Yusof and Hanafi 2015; Jung et al. 2011; Shakib et al. 2016; Parizad and Shahbazi 2016) and consequently could mitigate the formation damage.

In recent years, by the development of technology, artificial intelligence tools have widely applied in order to model nonlinear problems in various fields of science. Artificial neural network (ANN) is one of the most common tools that are utilized. Predicting the filtration properties of drilling fluids is also investigated in some recent researches in the absence of nanoparticles (Jeirani and Mohebbi 2006); however, no model is presented to see the effect of nanoparticles on filtration properties of drilling fluids yet.

In this study, the influence of various nanoparticles on filtration volume is considered by applying an ANN model as a novel method. For this purpose, a total of 1003 data points are gathered from the most recent researches found in the literature. Then, the ANN model is developed for accurate prediction of filtration volume of water-based drilling fluid as a function of effective parameters such as nanoparticle type, nanoparticle concentration, KCl salt concentration, temperature, pressure, round per minute (RPM), and time. The assessment of the proposed model is evaluated by statistical analyses. Finally, a sensitivity analysis is performed to determine the most sensitive parameters on the filtration volume.

Preview of artificial neural network

Artificial neural network (ANN) is known as a processing system that is used to obtain a nonlinear regression model between variables benchmarked from human brain. ANN constructs a nonlinear mapping between inputs and outputs and converts these complex relationships to a series of training patterns which could be useful for wherever the mathematical modeling may be too complicated (Liang and Bose 1996). A network usually consists of at least three layers: input layer, one hidden layer, and output layer. Each layer consists of some neurons in order to connect to each other. A neuron is an individual processing unit which includes in the modeling process. Neurons are connected to each other through a transfer function which consists of the weights and bias. Input parameters are multiplied by their associated weights and then summed with their associated bias. The performance of an ANN model depends on both the weights and the transfer function (Masoudi et al. 2018). The general mathematical expression of each neuron is given in the following:

$$O_{i} = \sigma \left( {Y_{i} } \right) = \sigma \left( {\mathop \sum \limits_{j = 1}^{N} w_{ji} P_{j} + b_{i} } \right)$$
(1)

where Oi is the output of ith neuron, Yi is the ith input to the function, σ is transfer function, N is the number of neurons in each layer, wji is the weights that connects the ith neuron to the other neurons of the next layer for jth input parameter, Pj is the jth input parameters, and bi is the bias of the ith neuron.

The initial weights are set as random numbers and are corrected during the training process of the network. Three steps are performed in order to develop an ANN model: building the model; model training; and testing procedure (Kassem et al. 2018). The most common training algorithm utilized in the training process is back-propagation (BP). This training process consists of two phases: feed-forward phase, in which the knowledge is processed from the input layer to the output layer, and back-propagation phase, in which the difference between network output values obtained in the first phase and desired output value is compared with previously determined difference tolerance and the error is propagated backward to update the links in the input layer (Kassem et al. 2018). The weights and biases are adjusted through the training process to minimize the error in each step. The adjustment of weights is also done through the training algorithm that the best one is Levenberg–Marquardt training algorithm (TRAINLM). The weight difference for a given neuron is calculated by gradient descent with momentum weight and bias learning function (LEARNGDM) as:

$$dw_{{ji{\text{new}}}} = \left( {MC} \right) \times dw_{{ji{\text{prev}}}} + \left( {1 - MC} \right) \times LR \times gw_{ji}$$
(2)

where \(dw_{{ji{\text{new}}}}\) is the new weight change for ith neuron and jth input parameter, MC is the momentum constant, \(dw_{{ij{\text{prev}}}}\) is the previous weight change for ith neuron and jth input parameter, LR is the learning rate, and gwji is the weight gradient descent.

Among the various types of transfer functions, tangent sigmoid (TANSIG) and pure linear (PURELIN) functions are usually used for the inner and outer, respectively. The mathematical description for tangent sigmoid and pure linear functions is given in Eqs. 3 and 4, respectively:

$$\sigma = \frac{2}{{1 + \exp \left( { - 2Y_{i} } \right)}} - 1$$
(3)
$$\sigma = Y_{i}$$
(4)

All parameters of Eqs. 1 to 4 are dimensionless. The general architecture of an ANN model and a neuron structure is presented in Fig. 1.

Fig. 1
figure 1

a General architecture of an ANN model and b a neuron structure

Full size image

Methodology

Data collection

In this study, a data collection is used from the literature that relates the filtration volume of water-based drilling fluid to the effective input parameters. As said before, various nanoparticles are used by researchers in order to improve the drilling fluid properties. The data bank is gathered from those researches that the effect of nanoparticles on the filtration volume of water-based drilling fluid has been investigated. Some of the previous studies have also presented the effect of nanoparticles simultaneously with various polymers and surfactants. Such studies have not contributed in this research in order to model and investigate the effect of nanoparticles solely. Moreover, it is necessary to use dependable experimental results to construct a reliable network.

The utilized nanoparticles and their respective studies that are contributed in the data bank are SiO2 (Parizad et al. 2018), Fe2O3 (Vryzas et al. 2015; Mahmoud et al. 2017), CuO (Shakib et al. 2016), Al2O3 (Shakib et al. 2016), SnO2 (Parizad and Shahbazi 2016), and Clay (Shakib et al. 2016). The experimental data in these studies have included the impact of nanoparticle type, nanoparticle concentration (wt%), KCl salt concentration (wt%), temperature (°F), pressure (psi), RPM (round/min), and time (s) on filtration volume (ml) of water-based drilling fluid. The input parameter named nanoparticle type is considered as one of the input parameters to see the effect of different nanoparticles. A total number of 1003 data points are used for predicting model, which is described later in this paper. These data points are randomly divided into two categories that are named training data and testing data. In order to check the performance of the model in predicting the target, these two categories must be apart from each other and do not have any points in common. For this purpose, the training data consist of about 80% of the main data points that are 803 data points, and the remaining 20% of the main data points are used as testing data that are 200 data points. The statistical description of the data bank used in this study is given in Table 1.

Table 1 Statistical description of the data bank used in this study
Full size table

Model construction

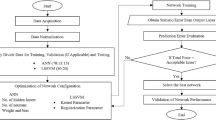
In order to predict the target, a feed-forward back-propagation algorithm is used. As said before, an ANN consists of some layers that are containing some neurons. An optimal network is a network with the optimum amount of layers and neurons, which must be obtained through the training process. TRAINLM and LEARNGDM are set as the training and adaption learning functions, respectively. The transfer functions that are used to connect the neurons are set TANSIG, TANSIG, and PURELIN in first, second, and third layer, respectively. The criterion that specifies the best network among the generated networks is set as MSE. A network has higher accuracy in predicting the target that has lower MSE and higher R2. Trial and error process is done for several times to find the optimal network. The best network is found with 3 layers (2 hidden layers and output layer) that the number of neurons is 21, 9, and 1 in first, second, and third layer, respectively. The workflow of model construction, model training, and sensitivity analysis (which is described later) is represented in Fig. 2. Training parameters of the proposed model are given in Table 2.

Fig. 2
figure 2

Workflow of model construction, model training, and sensitivity analysis

Full size image
Table 2 Training parameters of the proposed model
Full size table

Error assessment

After a model has been developed, the robustness of the model in predicting the target must be evaluated to see whether the model has the desired performance and accuracy. Measuring the data fitness of the model in predicting the target is determined by correlation coefficient (R2). As the criterion that is used in finding the optimal network, mean-squared error (MSE) is calculated as one of the most commonly used parameters. Also some other statistical parameters are calculated including root-mean-squared error (RMSE) that is the root of MSE; average relative error (ARE) that is the average value of RE; average absolute relative error (AARE) that is the absolute value of ARE; relative deviation (RE) that is the relative difference between actual and predicted values; and standard deviation (SD) between the actual and predicted data. Equations 5 to 11 express the definitions of the above parameters:

  1. 1.

    Correlation coefficient (R2):

    $$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {Y_{i}^{pr} - Y_{i}^{ac} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\overline{{Y^{ac} }} - Y_{i}^{ac} } \right)^{2} }}$$
    (5)
  2. 2.

    Mean-squared error (MSE):

    $$MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{i}^{pr} - Y_{i}^{ac} } \right)^{2}$$
    (6)
  3. 3.

    Root-mean-squared error (RMSE):

    $$RMSE = \left[ {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{i}^{pr} - Y_{i}^{ac} } \right)^{2} } \right]^{0.5}$$
    (7)
  4. 4.

    Average relative error (ARE):

    $$ARE\left( \% \right) = \left( {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{Y_{i}^{pr} - Y_{i}^{ac} }}{{Y_{i}^{ac} }}} \right) \times 100$$
    (8)
  5. 5.

    Average absolute relative error (AARE):

    $$AARE\left( \% \right) = \left( {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\frac{{Y_{i}^{pr} - Y_{i}^{ac} }}{{Y_{i}^{ac} }}} \right|} \right) \times 100$$
    (9)
  6. 6.

    Relative deviation (RD):

    $$RD\left( \% \right) = \frac{{Y_{i}^{pr} - Y_{i}^{ac} }}{{Y_{i}^{ac} }} \times 100$$
    (10)
  7. 7.

    Standard deviation (SD):

    $$SD = \left[ {\frac{1}{N - 1}\mathop \sum \limits_{i = 1}^{N} \left( {\frac{{Y_{i}^{pr} - Y_{i}^{ac} }}{{Y_{i}^{ac} }}} \right)^{2} } \right]^{0.5}$$
    (11)

In the above equations, N is the number of data; \(Y_{i}^{ac}\) is the actual data; \(Y_{i}^{pr}\) is the predicted data; and \(\overline{{Y^{ac} }}\) is the average of the actual data.

Sensitivity analysis

The concepts of sensitivity and uncertainty analysis are one of the essential parts of modeling and statistical studies. Sensitivity analysis determines the contribution of each input parameter to the output parameters of a model or a data series. In other words, sensitivity analysis quantifies how the input parameters would influence the output parameters. Also, it is defined as the contribution of each input parameter to the uncertainty in model predictions (Hammonds et al. 1994).Uncertainty analysis determines the uncertainty in each input parameter in model predictions (Hammonds et al. 1994).

Sensitivity analysis methods could be categorized as two points of view. Based on the concept, sensitivity analysis methods are categorized as deterministic and statistic (Zhou 2014). Statistical methods dealt with sensitivity analysis after the uncertainty analysis stage, while deterministic methods dealt with sensitivity analysis first and then go through the uncertainty analysis (Cacuci et al. 2005). Based on the factor space of interest, sensitivity analysis methods are categorized as local and global (Yang 2011). Local methods investigate the model behavior by varying each input parameter at a time (Zhou 2014). Global methods investigate the model behavior by varying all parameters over their ranges simultaneously (Zhou 2014).

Among the various approaches for sensitivity analysis, Monte Carlo method is one of the most utilized methods in several fields of engineering. In this method, random samples of the input parameters are generated by various distribution sampling types over the ranges of parameters. Then, it repeatedly simulates the model several times that each time a different set of generated parameters of the distribution is utilized. The output of the model is the probability of output results (Bonate 2001). Monte Carlo method provides an effective approach to assess the influence of several interacting parameters that could exhibit a wide range of uncertainties (Santoso et al. 2019). The generated runs by this method may not be representative of the full-physics models, and it requires an excessive number of runs (Santoso et al. 2019). In order to reduce the number of runs and develop an efficient model, design of experiment (DoE) is developed (Santoso et al. 2019).

In this study, the sensitivity analysis is performed by relevancy factor (RF). Each of the input parameters that have the higher (or lower) relevancy factor has a higher (or lower) impact on the filtration volume, respectively. The relevancy factor definition is given in the following expression:

$$RF\left( {P_{i} ,Y^{pr} } \right) = \frac{{\mathop \sum \nolimits_{j = 1}^{N} \left( {P_{i,j} - \overline{{P_{i} }} } \right)\left( {Y_{j}^{pr} - \overline{{Y^{pr} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{N} \left( {P_{i,j} - \overline{{P_{i} }} } \right)^{2} \mathop \sum \nolimits_{j = 1}^{N} \left( {Y_{j}^{pr} - \overline{{Y^{pr} }} } \right)^{2} } }}$$
(12)

where Pi is the ith input parameter, Pi,j is the jth value of the ith input parameter, \(\overline{{P_{i} }}\) is the average of ith input, \(Y_{j}^{pr}\) is the jth predicted filtration volume, N is the number of overall data, and \(\overline{{Y^{pr} }}\) is the average of the predicted filtration volume.

The results of the sensitivity analysis are given in the Results and Discussion section.

Results and discussion

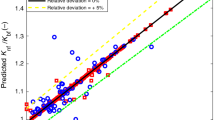
In order to evaluate the proposed model, the predefined statistical parameters are calculated. Also the predicted and actual data are plotted versus each other. Figure 3 represents the crossplot of the model predicted filtration volume versus the actual filtration volume for training, testing, and overall data. The y = x line is plotted in this figure to evaluate the precision of the proposed model. The precision of the model is determined via the tight accumulation of data points around the y = x line. The amount of this precision is usually measured by correlation coefficient. The correlation coefficient is calculated by fitting the best line that passes through the data, which has the lowest amount of this coefficient between all the other lines that could pass from the data.

Fig. 3
figure 3

Predicted versus actual filtration volume for a training data, b testing data, and c overall data

Full size image

To obtain a precise comparison between the proposed model output and the actual output, the obtained data from the model and the actual data are simultaneously plotted versus the index of data points in Fig. 4 for training, testing, and overall data. It could be seen that the predicted values of filtration volume closely fit the actual values.

Fig. 4
figure 4

Simultaneous representations of model data and actual data of filtration volume for a training data, b testing data, and c overall data

Full size image

The values of R2 for training, testing, and overall data in this figure are 0.9938, 0.9904, and 0.9928, respectively. These values exhibit the efficiency of the employed ANN model to predict the filtration volume. The other statistical parameters are represented in Table 3. The table shows that the values of MSE, AARE, and SD for overall data are 0.4797, 2.6636, and 0.0585, respectively. It is clear from the table that the proposed model has the high performance and could estimate and predict the filtration volume precisely.

Table 3 Statistical parameters of the proposed ANN model
Full size table

In order to better understanding and comparing the values of each statistical parameter with each other between each dataset, it is better to declare another representation of these parameters. Figure 5 depicts a graphical representation of measured statistical parameters for training, testing, and overall data.

Fig. 5
figure 5

Graphical representation of aR2, b MSE, c RMSE, d ARE, e AARE, and f SD for training, testing, and overall data

Full size image

Figure 6 represents a basecase from the databank (Parizad et al. 2018) in order to compare the filtration volume before and after adding nanoparticles and also to observe the physics happening to drilling fluid system. In this figure, the dashed and the continuous lines belong to base (without nanoparticles) drilling fluid case and the case with nanoparticles, respectively. First of all, this figure depicts that the presented model could fit the actual data and also could predict the trend of actual data. As shown in the figure, in the base drilling fluid (without nanoparticles) and also in the case with nanoparticles, filtration volume increases by increasing temperature. By comparing the curves before and after adding nanoparticles, it could be seen that the filtration volume decreases by increasing nanoparticles. There is also a range that nanoparticles could do their best in lowering the filtration volume that is stated in the literature (Mahmoud et al. 2017).

Fig. 6
figure 6

Simultaneous actual and model filtration volume at various temperatures: before adding nanoparticles (base drilling fluid) and after adding nanoparticles

Full size image

The relative deviation that measures the difference between predicted and actual data gives an illustrative view about the adjacency of actual and model target. The range of relative deviation values for training, testing, and overall data is [− 3.9797, 7.1553], [− 2.8577, 3.4762], and [− 3.9797, 7.1553], respectively. Such a low value of relative deviation illustrates the consistency between the actual and predicted filtration volume as presented in Fig. 7 for training, testing, and overall data. The statistical values of relative deviation are given in Table 4.

Fig. 7
figure 7

Relative deviation versus actual filtration volume for a training data, b testing data, and c overall data

Full size image
Table 4 Statistical values of RD (%)
Full size table

The distribution plots explore the distribution of a specific parameter across the whole data points that are considered in the study. Distribution of relative deviation is shown in Fig. 8 for training, testing, and overall data. The curve that is plotted on the overall data bars is the normal distribution curve. As it can be seen from the figure, the distribution of the relative deviation is located in the vicinity of zero that represents the uniform consistency between the actual and predicted data across the whole data points.

Fig. 8
figure 8

Distribution of relative deviation for a training data, b testing data, and c overall data

Full size image

A specific parameter that is measured in all parts of the science is affected by some other independent parameters that must be considered during the measurement. It is obvious that all the effective parameters do not have the same effect on that specific parameter. Some of these parameters impact the specific parameter more and some less. As said before, sensitivity analysis is a method for the assessment of the effect of independent parameters on a specific parameter. Then, to specify the effect of each effective parameter on the filtration volume, a sensitivity analysis is done. Various methods are available to present the sensitivity analysis. In this work, relevancy factor is used (which is discussed in the Sensitivity Analysis section). Figure 9 represents the results of the sensitivity analysis of all input parameters on the filtration volume. It is obvious from this figure that in modeling the filtration volume, the most sensitive parameter is nanoparticle concentration and the least sensitive parameter is RPM. This result should be considered by the researchers for further researches.

Fig. 9
figure 9

Sensitivity analysis of filtration volume

Full size image

Conclusions

In this study, an ANN model is developed to predict the effect of nanoparticles on filtration volume of water-based drilling fluids. For this purpose, 1003 data points are gathered from the most recent researches. Influencing parameters including in this data bank are nanoparticle type, nanoparticle concentration, KCl salt concentration, temperature, pressure, RPM, and time. Nanoparticles that are engaged are SiO2, Fe2O3, CuO, Al2O3, SnO2, and clay. The superiority of the model confirms by evaluating the statistical analyses with AARE, R2, and MSE values of 2.6636%, 0.9928, and 0.4797, respectively, for total data. Moreover, sensitivity analysis showed filtration volume is more sensitive to nanoparticle concentration and this parameter should be considered by researchers during process optimization. The proposed ANN model is capable and efficient and comprehensive in predicting the influence of various nanoparticles on filtration volume of water-based drilling fluids.