Advertisement

A new approach to reduce uncertainty in reservoir characterization using saturation height modeling, Mesaverde tight gas sandstones, western US basins

  • Amirhossein Abdollahian
  • Mehdi Tadayoni
  • Radzuan Bin Junin
Open Access
Original Paper - Exploration Geology
First Online:
  • 186 Downloads

Abstract

Tight gas sandstone (TGS) reservoirs are one of the most integral parts of the unconventional reservoirs pyramid. Uncertainty in petrophysical properties of a TGS reservoir will cause great challenges in reservoir characterization and also 3D properties modeling. The main goal of this study is to implement a new workflow based on saturation height modeling (SHM) to reduce this uncertainty in a TGS reservoir by acquiring a global in situ water saturation function and also calculating more accurate permeability values. Capillary pressure curves and well logs from ten different wells in four different giant basins of western US TGS reservoirs are the input data in this study. After grouping the capillary pressure curves based on the corresponding cores sorting, size, and texture, and also applying some initial corrections, five different SHM methods have been applied to each group. Using regression methods, the function of each model has been rewritten based on the cores’ petrophysical properties. By entering the porosity and permeability logs of each well in the rewritten functions and by implementing the height above free water level (HAFWL), a water saturation profile has been calculated for each well. Using standard error of estimate analysis between the calculated water saturation profile and the log-based water saturation profile as the base one, the most reliable SHM method has been recognized. Using water saturation and porosity logs and also HAFWL value in each well, accurate permeability values have been calculated based on the saturation height function of the best model. Finally, the regression method between the calculated permeability and the accurate cores permeability values approves the reliability of the results.

Keywords

SHM MICP Permeability In situ water saturation 

List of symbols

\((P_{\mathrm{c}})_{\mathrm{stress}\text{-}{\mathrm{corr}}}\)

Stress-corrected capillary pressure (psi)

\((P_{\mathrm{c}})_{\mathrm{lab}}\)

Laboratory capillary pressure (psi)

\(\phi _{\mathrm{res}}\)

Core porosity at reservoir conditions, fraction

\(\phi _{\mathrm{lab}}\)

Core porosity at laboratory conditions, fraction

\(\sigma\)

Interfacial tension (dyne/cm)

\(\theta\)

Contact angle \((^{\circ })\)

\(S_{\mathrm{w}}\)

Water saturation, fraction

\(S_{\mathrm{wirr}}\)

Irreducible water saturation, fraction

K

Permeability (mD)

Introduction

Although the conventional hydrocarbon reservoirs are playing the most important role in meeting the energy demand of the today’s world, this role will be degraded in a few next decades because of dramatic development of unconventional reservoirs. Unconventional reservoirs include: coal bed methane (CBM), oil shale, tight gas sandstone (TGS), organic-rich shale, and also hydrates. TGS reservoirs are one of the most integral parts of the unconventional reservoirs pyramid. According to the United States government gas policy in the 1970s, a tight gas reservoir is one with gas flow permeability less than 0.1 mD. This definition is only based on a governmental tax decision. “The best definition of tight gas reservoir is a reservoir that cannot be produced at economic flow rates nor recover economic volumes of natural gas unless the well is stimulated by a large hydraulic fracture treatment or produced by use of a horizontal wellbore or multilateral wellbores” (Holditch 2006).

Permeability and in situ water saturation values are essential data for reservoir characterization and also 3D properties modeling. Using saturation height modeling (SHM), it is possible to calculate permeability more precisely and predict in situ water saturation based on petrophysical properties. In this study, different saturation height models have been applied on Mesaverde TGS reservoirs which are one of the most important parts of unconventional gas reservoirs in western US basins. The input data include some parts of core analysis and well logs from ten different wells in four different basins including: Washakie, Uinta, Piceance, and Upper Greater Green River (Byrnes et al. 2008). The main goal of this study is to implement a new workflow based on SHM to reduce the uncertainty in reservoir characterization of such a vast area with four giant basins by acquiring a global in situ water saturation function and also computing the permeability values in a more accurate way. Uncertainty reduction in 3D properties modeling could be another advantage of this workflow.

Method and theory

To attain the goals of this study by means of SHM, a workflow including five subsequent steps is introduced here (Fig. 1).
Open image in new windowFig. 1
Fig. 1

The workflow of this study

Capillary pressure data classification

There are three main methods for measuring the capillary pressure curve of a core: Porous Plate, Centrifugal, and Mercury Injection Capillary Pressure (MICP) method. In comparison to the other methods, the MICP method is more common in petroleum industry because of its rapidness and low measurement costs (Dandekar 2013). Capillary pressure curves in this study are based on air-mercury MICP measurements in which the air is the wetting phase and the mercury is the nonwetting phase, respectively (Byrnes et al. 2008). According to the laboratory analysis, the corresponding cores of the MICP data in this study could be classified into four groups based on their size, sorting, and texture:

Group 1: Moderately shaly sandstones with 10–40% clay and silt (12 cores)

Group 2: Very fine sandstones (6 cores)

Group 3: Fine sandstones (11 cores)

Group 4: Medium sandstones (17 cores)

Grouping the MICP curves using this classification could increase the SHM accuracy.

Capillary pressure data correction

It is obvious that only a corrected input data can lead us to the desirable goals from SHM. Therefore, four corrections have been applied to the MICP curves subsequently.

Out of trend data elimination

There might be some out of trend curves in the capillary pressure data because of poor core condition or laboratory measurement errors. It is crucial to detect and eliminate these kinds of curves by graphical evaluation of total capillary pressure data in each group. After this correction, 5 out of 46 capillary pressure curves have been removed. Figure 2 illustrates one of the out of trend curves before the elimination.
Open image in new windowFig. 2
Fig. 2

One of the out of trend capillary pressure curves in the group 4 which is marked by red color

Closure correction

In the first few steps of capillary pressure measurements, the nonwetting phase (e.g., mercury in the MICP experiment) will occupy the core surface asperities which are not the members of the actual pore system. “The pressure at which mercury commences to occupy the actual pore system of the sample being tested is called the initial pore entry pressure or closure pressure. All intrusion data recorded up to this initial entry pressure are subtracted from the MICP raw data output as the closure correction” (Shafer and Neasham 2000). Figure 3 shows the effect of closure correction on one of the curves.
Open image in new windowFig. 3
Fig. 3

Effect of closure correction on one of the capillary pressure curves

Stress correction

In comparison to the reservoir conditions, stress is much lower in the laboratory measurements. This stress relief consequences in porosity and permeability increase, pore entry pressure reduction, and also capillary pressure curve changes (McPhee et al. 2015). The stress correction which is applied to the laboratory measurements is derived by Juhasz from Shell in the 1979 (Juhasz et al. 1979):
$$\begin{aligned} (P_{\mathrm{c}})_{\mathrm{stress}\text{-}{\mathrm{corr}}} = (P_{\mathrm{c}})_{\mathrm{lab}} \left( \frac{(\phi )_{\mathrm{res}}}{(\phi )_{\mathrm{lab}}} \right) ^{-0.5}. \end{aligned}$$
(1)
The effect of stress correction on one of the capillary pressure curves is illustrated in Fig. 4.
Open image in new windowFig. 4
Fig. 4

Black capillary pressure curve has been changed to the red one after applying the stress correction

Conversion to reservoir fluid conditions

In laboratory measurements, the contact angle and also the interfacial tension will vary from reservoir condition because of different nonwetting and also wetting phase fluids. It is possible to eliminate the effect of this variation on capillary pressure curves using Eq. 2 (Purcell 1949):
$$\begin{aligned} (P_{\mathrm{c}})_{\mathrm{res}} = \frac{(\sigma \cos \theta )_{\mathrm{res}}}{(\sigma \cos \theta )_{\mathrm{lab}}}(P_{\mathrm{c}})_{\mathrm{lab}}. \end{aligned}$$
(2)
According to the input data (Byrnes et al. 2008), all laboratory measurements assume \(\sigma = 484\,\text{dyne}/\text{cm}\) and \(\theta = 140\,\text{deg}\). These data also represent the reservoir in situ gas–brine condition by \((\sigma \cos \theta )_{\mathrm{res}} = 40\,\text{dyne}/\text{cm}\).

Applying different saturation height models

“A saturation height model is an equation that represents the water saturation profile in a reservoir interval as a function of the fluid/rock properties and the distance above the Free Water Level (FWL) and is constructed from capillary pressure data” (Valentini et al. 2017). There are many Saturation Height Models with specific fitting parameters which are in use in petroleum industry. To predict the in situ water saturation in an un-cored depth of a reservoir, it is crucial to generalize these models. This generalization is possible using regression methods between fitting parameters of a model and cores’ petrophysical properties (like porosity, permeability, and also square root of permeability/porosity). In this study, we applied five important Saturation Height Models on each of the groups.

Brooks–Corey (Brooks and Corey 1964)

This model is one of the most conventional Saturation Height Models in petroleum industry. Based on the Brooks–Corey model, each capillary pressure curve could be approximated by a unique curve with three fitting parameters: \(S_{\mathrm{wirr}}\), \({P_{\mathrm{ce}}}\), and also N:
$$\begin{aligned} S_{\mathrm{w}} = S_{\mathrm{wirr}}+(1- S_{\mathrm{wirr}})\left( \frac{P_{\mathrm{ce}}}{P_{\mathrm{c}}}\right) ^{\frac{1}{N}}. \end{aligned}$$
(3)
Using the regression methods between the fitting parameters of the model and cores’ petrophysical properties, it is possible to rewrite the fitting parameters in Eq. 3 based on cores’ petrophysical properties. As an example, in part (a) of Fig. 5, each capillary pressure curve in the group 1 (in gray color) has been approximated by the Brooks–Corey model (in red color). In part (b), the relations between the fitting parameters of the model and the cores petrophysical properties (\(\phi\), K, and also \(\sqrt{\frac{K}{\phi }}\)) have been investigated using regression methods. The \(S_{\mathrm{wirr}}\) has been set to zero as a numerical artifact. Finally, and in part (c), rewriting Eq. 3 based on regression results, it is possible to calculate the capillary pressure curves using the petrophysical properties (red color curves).
Open image in new windowFig. 5
Fig. 5

Steps to acquire global Brooks–Corey function in the group 1 of the data

Leverett-J (Leverett et al. 1941)

According to this model, if capillary pressure curves of a bundle of cores with relatively similar pore sizes re-plotted based on \(J_{(\mathrm{SW})}\) versus \(S_{\mathrm{w}}\) (in which \(J_{(\mathrm{SW})}\) is called “J-function” and has been elucidated in Eq. 4), it is possible to express each capillary pressure curve by a global function (Eq. 5):
$$\begin{aligned}J_{(\mathrm{SW})} = \frac{P_{\mathrm{c}}}{\sigma \cos \theta }\sqrt{\frac{K}{\phi }} \end{aligned}$$
(4)
$$\begin{aligned}J = a (S_{\mathrm{w}})^{b}, \end{aligned}$$
(5)
where a and b are the fitting parameters of the model. Figure 6 represents the capillary pressure curves of the group 3 (in gray color) and also their approximation after applying the Leverett-J model.
Open image in new windowFig. 6
Fig. 6

Capillary pressure curves of the group 3 (in gray color) have been changed to the red curves after applying the Leverett-J model

Skelt–Harrison (Skelt et al. 1995)

This model correlates the water saturation to the height above free water level (HAFWL):
$$\begin{aligned} S_{\mathrm{w}}=1-A {\mathrm{e}}^{\left( -\left( \frac{B}{h+D}\right) ^{C}\right) }, \end{aligned}$$
(6)
where A, B, C,  and D are the parameters of the model, and h is HAFWL in meter.
The capillary pressure curves of the group 4 (in gray color) have been changed to the red curves after applying the Skelt–Harrison model (Fig. 7).
Open image in new windowFig. 7
Fig. 7

Capillary pressure curves of the group 4 (in gray color) and also their approximation (in red color) after applying the Skelt–Harrison model

Lambda (Wiltgen et al. 2003)

Using Eqs. 7 and 8, this model can relate the water saturation to the HAFWL:
$$\begin{aligned}S_{\mathrm{w}}=A h^{-\lambda }+B \end{aligned}$$
(7)
$$\begin{aligned}\lambda ={\mathrm{e}}^{(A+B \ln (\phi \frac{e}{100}))}, \end{aligned}$$
(8)
where A, B, and \(\lambda\) are the parameters of the model, and h is HAFWL in meter.
As an example, Fig. 8 illustrates the capillary pressure curves of the group 4 before and after applying the Lambda model.
Open image in new windowFig. 8
Fig. 8

After applying the Lambda model, the capillary pressure curves of the group 4 (in gray color) have been changed to the red curves

Thomeer (Thomeer et al. 1960)

According to this model, the pore geometric factor (G) could affect the shape and location of capillary pressure curves dramatically. The original equation is based on bulk mercury saturation which is the product of porosity and mercury saturation. It could be rewritten in the form of Eq. 9:
$$\begin{aligned} S_{\mathrm{w}} = S_{\mathrm{wirr}}+(1- S_{\mathrm{wirr}})\left( 1-{\mathrm{e}}^{\frac{G}{\ln (\frac{p_{\mathrm{ce}}}{p_{\mathrm{c}}})}}\right) . \end{aligned}$$
(9)
Figure 9 illustrates the group 3 curves (in gray color) and the subsequent red curves after applying the Thomeer model.
Open image in new windowFig. 9
Fig. 9

Group 3 curves (in gray color) and the subsequent red curves after applying the Thomeer model

By plotting each of the constants of a specific SHM equation versus porosity, permeability, and square root of permeability/porosity and also using regression methods, it is possible to rewrite the equation as a function of the mentioned petrophysical properties.

Acquiring a global in situ water saturation function

Using porosity and permeability logs of each well as the inputs of the generalized models and also using Eq. 10 to change the HAFWL into capillary pressure, the water saturation values in all depths of each well have been calculated:
$$\begin{aligned} \text{HAFWL}=\frac{ (P_{\mathrm{c}})_{\mathrm{res}}}{(\rho _{\mathrm{wat}}-\rho _{\mathrm{gas}})_{\mathrm{reservoir}} (g)}, \end{aligned}$$
(10)
where \(\rho _{\mathrm{wat}}\) and \(\rho _{\mathrm{gas}}\) are the water and the gas density, respectively, and g is the gravitational constant.
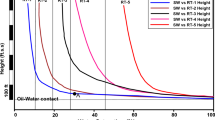
Comparing the calculated water saturations from each model with the water saturation curve obtained from the well logs as the base one, it is possible to determine the most accurate model. Figure 10 illustrates the calculated water saturation curves from the Lambda model of the group 4 and also water saturation curves from well logs in medium sandstone intervals of all three wells in Piceance basin simultaneously. By eye balling, it can be concluded that the accuracy of this model is low, medium, and high from the left to the right, respectively.
Open image in new windowFig. 10
Fig. 10

Illustration of the water saturation curves from well logs and the Lambda model (group 4) in all three wells of the Piceance basin (medium sandstone intervals)

Although curve illustrations can give us a bird’s eye view in selecting the best saturation height model, but it is necessary to use statistical analysis like standard error of estimate (SEE) or regression methods (Sohrabi et al. 2007). To select the best SHM method, we used the SEE analysis for all of the wells in this study (Eq. 11):
$$\begin{aligned} \text{SEE}=\sqrt{\frac{\sum _{1}^{n}(\text{SW}_{\mathrm{model}}-\text{SW}_{\mathrm{log}})^{2}}{n-1}}. \end{aligned}$$
(11)
As an example, Table 1 represents the SEE values for one of the wells in the Washakie basin considering medium sandstone intervals (all values have been calculated from the group 4 models). According to the total analysis of the SEE values in all of the wells, the Brooks–Corey model is the most accurate method, while the Leverett-J model is the less accurate one (this could be a consequence of oversimplified assumptions of this method which are based on a bundle of straight and perfect capillary tubes).
Table 1

Water saturation SEE values of medium sandstone intervals of a well in the Washakie basin (based on the group 4 models)

Model

SEE

Brooks–Corey

0.196

Lambda

0.213

Skelt–Harrison

0.208

Leverett-J

0.349

Thomeer

0.205

Calculating accurate permeability values using SHM

Reducing uncertainty in permeability values and increasing their accuracy are extremely important in reservoir characterization and also 3D properties modeling. As water saturation log, HAFWL value, and porosity log are available for different intervals of wells, the permeability profiles have been calculated based on the most reliable model (Brooks–Corey) saturation height function in each group (Fig. 11).
Open image in new windowFig. 11
Fig. 11

Calculating permeability using saturation height function

High regression coefficient of determination \((R^{2})\) between the calculated and core permeability values approves the result (Fig. 12). Here, the \(R^{2}\) is equal to 0.652 and the regression formula is:
$$\begin{aligned} \log (K_{\mathrm{core}})=1.745528 ({\mathrm{e}}^{\log (K_{\mathrm{model}})})-1.708569. \end{aligned}$$
(12)
Open image in new windowFig. 12
Fig. 12

Using regression method between the calculated and the cores permeability values to approve the accuracy of the calculated permeability values

Conclusions

Uncertain petrophysical properties can cause fundamental problems in unconventional reservoir characterization and also 3D properties modeling. Reducing this uncertainty by implementing a new workflow based on saturation height modeling is the main goal of this study. Capillary pressure curves and well logs from ten different wells in four different giant basins of western US tight gas sandstone reservoirs are the input data in this study. The capillary pressure curves have been classified based on cores sorting, size, and texture. After correcting the curves in four subsequent steps, five different saturation height models have been applied on each class: Brooks–Corey, Lambda, Skelt–Harrison, Leverett-J, and Thomeer. Using regression methods, the function of each model has been rewritten based on the cores petrophysical properties. A water saturation profile has been calculated for each well by entering its porosity and permeability logs in the rewritten functions and also using HAFWL values. After employing the SEE analysis to compare the log-based with the calculated water saturation profiles, the Brooks–Corey has been recognized as the most accurate model. Finally, precise permeability values have been calculated for each well by entering its porosity and water saturation logs and also HAFWL values in the Brooks–Corey saturation height function of each group. The accuracy of the results has been approved by high coefficient of determination \((R^{2})\) between the calculated and the cores’ permeability values.

Notes

Acknowledgements

The authors would like to thank Universiti Teknologi Malaysia (UTM) for its financial supports.

References

  1. Brooks R, Corey A (1964) Hydraulic properties of porous media. Hydrology papers, vol 3. Colorado State University, Fort Collins, pp 22–27Google Scholar
  2. Byrnes A, Cluff R, Webb J, Victorine J, Stalder K, Osburn D, Knoderer A, Metheny O, Hommertzheim T, Byrnes J et al (2008) Analysis of critical permeabilty, capillary pressure and electrical properties for Mesaverde tight gas sandstones from western us basins. Technical report, University of Kansas Center for Research IncorporatedGoogle Scholar
  3. Dandekar AY (2013) Petroleum reservoir rock and fluid properties. CRC Press, Boca RatonGoogle Scholar
  4. Holditch SA (2006) Tight gas sands. J Pet Technol 58(6):86–93CrossRefGoogle Scholar
  5. Juhasz I et al (1979) The central role of Qv and formation-water salinity in the evaluation of shaly formations. In: SPWLA 20th Annual Logging Symposium, p 26Google Scholar
  6. Leverett M et al (1941) Capillary behavior in porous solids. Trans AIME 142(01):152–169CrossRefGoogle Scholar
  7. McPhee C, Reed J, Zubizarreta I (2015) Core analysis: a best practice guide, vol 64. Elsevier, AmsterdamGoogle Scholar
  8. Purcell W (1949) Capillary pressures-their measurement using mercury and the calculation of permeability therefrom. J Pet Technol 1(2):39–48CrossRefGoogle Scholar
  9. Shafer J, Neasham J (2000) Mercury porosimetry protocol for rapid determination of petrophysical and reservoir quality properties. In: International symposium of the society of core analysts, SCA, vol 2021, p 12Google Scholar
  10. Skelt C, Harrison B et al (1995) An integrated approach to saturation height analysis. In: SPWLA 36th annual logging symposium, Society of Petrophysicists and Well-Log AnalystsGoogle Scholar
  11. Sohrabi M, Jamiolahmady M, Tafat M et al (2007) Estimation of saturation height function using capillary pressure by different approaches. In: EUROPEC/EAGE conference and exhibition, Society of Petroleum EngineersGoogle Scholar
  12. Thomeer J et al (1960) Introduction of a pore geometrical factor defined by the capillary pressure curve. J Pet Technol 12(03):73–77CrossRefGoogle Scholar
  13. Valentini S, Bernorio D, Grandis M, Mazzacca A, Serrao A, Visconti L et al (2017) Saturation height modelling: an integrated methodology to define a consistent saturation profile. In: Offshore Mediterranean conference and exhibitionGoogle Scholar
  14. Wiltgen NA, Le Calvez J, Owen K et al (2003) Methods of saturation modeling using capillary pressure averaging and pseudos. In: SPWLA 44th annual logging symposium, Society of Petrophysicists and Well-Log AnalystsGoogle Scholar

Copyright information

© The Author(s) 2018

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.University of TehranTehranIslamic Republic of Iran
  2. 2.Faculty of Petroleum and Renewable Energy EngineeringUniversiti Teknologi Malaysia (UTM)Johor BahruMalaysia

Personalised recommendations