Introduction

Chokes are key equipment installed at the wellhead of almost all producing oil, gas, and gas condensate wells. Wellhead chokes control and stabilize production flow rates of single or multiple phases, which is essential to prevent reservoir damage by creating a back pressure on the reservoir. Wellhead chokes also maintain the integrity and safety of surface production equipment (downstream of the wellhead), prevent water or gas coning within the reservoir, limit sand production from the reservoir in the flow stream, and provide flexible adjustments that can be used to adjust production rates and ultimate resource-recovery rates for a wide range of reservoir conditions (Guo 2007; Nasriani and Kalantariasl 2011; Mirzaei-Paiaman and Nourani 2012; Mirzaei-Paiaman and Salavati 2013).

Flow through a wellhead choke can be critical or sub-critical (Zarenezhad and Aminian 2011). From the perspective of controlling solid and fines production in a well production flow stream, the critical flow rate represents a production threshold rate above which the production of solids contained within the produced flow stream is uniform. Maintaining sub-critical flow conditions can be important in reservoirs prone to sand or fines production. When the flow rate exceeds this threshold (i.e., becomes critical), the production of sand and fines increases significantly.

Critical flow typically occurs when the pressure upstream of the wellhead is at least 70% higher than the pressure downstream of the wellhead, or when the ratio of downstream pressure to upstream pressure is 0.588 or less. If the ratio of downstream pressure to upstream pressure is greater than 0.588, sub-critical flow conditions prevail (Beiranvand et al. 2012). When critical flow conditions prevail, the flow rate is primarily a function of upstream pressure, gas oil ratio (GOR), and the choke aperture diameter. In critical flow conditions pressure changes in the flow lines downstream of the wellhead do not affect the flow rate therein. Since the liquid production rate through wellhead chokes is affected by changes in their aperture diameter (i.e., choke size), modeling and simulating the rate of flow through chokes of various aperture diameters for specific oil/gas field conditions enables production engineers to better understand and control production flow conditions.

Studies on wellhead chokes and their impacts on production flow rates began with Tangren et al. (1949) and their analysis of flow rate through restrictions. That analysis focused only on critical flow conditions and revealed that when gas bubbles are added to incompressible fluids, they prevent the upstream pressure from being transferred downstream of the restriction. Gilbert (1954) conducted pioneering work on production well-test data and analyzed 260 test datasets for choke sizes from 6/64 to 18/64 in. to derive an experimental relationship for critical flow (Eq. 1)

$${P_{{\text{wh}}}}=\frac{{C{R^m}Q}}{{{S^n}}}$$
(1)

where C, m, and n are experimental coefficients, which can be calculated when there is sufficient data (Al-Ajmi et al. 2015). Pwh is wellhead pressure (psig). R is gas to liquid ratio (SCF/STB). Q is flow rate (STB/day). S is choke size (1/64 in.).

Gilbert’s equation became the basis for many subsequent studies and adaptions beginning with Baxendell (1958), and with Ros (1960) addressing sub-critical as well as critical flow regimes. Achong (1961) claimed an improved relationship based upon a dataset of 104 well tests through chokes with 1/2 to 4 in. Poettmann and Beck (1963) adapted Ros’s model for field application, proposing a relationship for critical flow conditions that depends on upstream and downstream pressures.

Two relationships for critical and sub-critical flows were derived by Fortunati (1972), applying the Guzov and Medivedive log for sub-critical flow. Ashford (1974) proposed a model addressing two-phase critical flow through wellhead chokes further developing the model of Ros (1960). Abdul-Majeed (1988), based on data from 155 well tests from eastern Baghdad oilfields developed an experimental model, based on the Gilbert equation, demonstrating an absolute error of about 6%.

Using 97 well-test datasets and with choke diameters ranging from 24/64 to 128/64 in., Al-Attar (2008) developed an equation that predicts choke performance for sub-critical conditions. Beiranvand et al. (2012) proposed two formulas for estimating the liquid critical flow rate, based on 748 experimental data records including measured data for the input parameters of wellhead pressure, gas–liquid ratio, surface wellhead choke size, and the percentage of water, sediment, and emulsion. Mirzaei-Paiaman and Salavati (2013) investigated the effect of gas-specific gravity and oil-specific gravity on liquid flow rate. According to a statistical analysis of their results, they concluded that neither gas-specific gravity nor oil-specific gravity had a significant effect on flow rate. 704 test datasets from 31 wells in field A were used by Al-Ajmi et al. (2015) to develop a model for flow rate through chokes applying an artificial neural network (ANN) algorithm. Their model resulted in a calculated absolute error for that dataset of 13.92%. Choubineh et al. (2017a, b) improved predictions of wellhead choke liquid critical flow rates, applying a model based on a neural network hybridized with a training-learning-based optimization algorithm, to 113 data points from 12 oil wells in south Iran, achieving an average relative error of 2.09%. Ghorbani et al. (2017) optimized gas flow predictions for 92 datasets from the Pazanan gas condensate field (Iran) applying a firefly algorithm to successfully minimize the mean square error between measured and predicted gas flow rates from a wellhead test dataset.

Our objective here is to provide a new model for estimating oil flow through wellhead chokes improving upon the Gilbert’s equation and derivatives of it. Based on this formula, the liquid flow rate is as a function of three parameters such as wellhead pressure, choke size, and gas–liquid ratio. Since almost all models available in the literature used these three variables to predict the flow rate, we decided to include a new parameter named basic sediment and water (BS&W) to develop a model with new parameters and better performance. Also, it is necessary to say that the temperature did not have any significant impact on the flow rate based on relevancy factor formula; not including it in the new model (Discussion section). Another novelty is that it uses a mean square error (MSE) function test as the single-objective function for the GA and Solver algorithms, and then applies the optimized formula to a testing data subset, that is evaluated in terms of a set of statistical accuracy and correlation measures. A dataset of 182 wellhead choke measurements from wells drilled in the Reshadat oil field, located offshore southwest of Iran, is used to evaluate models to predict liquid flow rates through wellhead chokes (see Appendices 1, 2 and 3 for details of the reservoir and individual data record values).

Flow-rate prediction model incorporating optimization with a genetic algorithm

Our objective is to build optimization models that can estimate the liquid flow rate through wellhead chokes as accurately as possible. To achieve this objective, suitable mathematical tools are required. In recent decades, numerous optimization algorithms have been published and refined to find the best solution for optimization problems. We have selected a genetic optimization algorithm (GA) and standard Excel Solver non-linear and evolutionary optimization algorithms because of their simplicity, transparency, and general availability. The procedures for setting up and applying these algorithms are explained here.

A standard genetic algorithm (GA) is applied in this study as an optimization tool to assist in rapidly establishing the most accurate flow-rate prediction models in a novel easy to apply, transparent methodology that can be easily adapted to datasets (populations) of various sizes from other oil fields.

Genetic algorithms (GA) are robust stochastic evolutionary algorithms widely applied for solving optimization challenges in many scientific and industrial fields. The GA concept was initially proposed and exploited in the 1960s and 1970s (Holland 1975), and further developed with improved computation power in the 1980s and 1990s (Goldberg 1989; Jefferys 1993; Mitchell 1996). GA methodologies have continued to be refined in the past decade (e.g., Gen and Cheng 2008; Sivanandam and Deepa 2008) and are now frequently applied to provide multi-objective optimization solutions for various oil and gas engineering (Mansouri et al. 2015) and portfolio (Wood 2016) challenges.

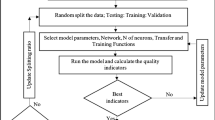
The GA, therefore, offers a well-established, evolutionary optimization method suitable for application to many non-linear optimization problems. Genetic algorithms are easy to apply in a consistent and transparent manner (Fig. 1), involving relatively few control parameters.

Fig. 1
figure 1

Flow diagram for the sequence involved in a generic genetic algorithm for optimization analysis

Full size image

The methodology adopted here for predicting liquid flow rate involves a sequence of 12 steps, described in detail in a flow diagram (Fig. 2). It incorporates a customized genetic optimization algorithm, which optimizes a fitness function defined by Eqs. 2 and 3

Fig. 2
figure 2

Flow diagram for the customized methodology to optimize wellhead choke oil flow-rate prediction incorporating a genetic algorithm

Full size image
$${\text{Fitness}}(f)=\mathop \sum \limits_{{i=1}}^{n} {{{{\left( {{y_i} - {{\hat {y}}_i}} \right)}^2}} \mathord{\left/ {\vphantom {{{{\left( {{y_i} - {{\hat {y}}_i}} \right)}^2}} {(n)}}} \right. \kern-0pt} {(n)}}$$
(2)

where

$${\hat {y}_i}=\frac{{{P_{{\text{wh}}}}{{\left( {{D_{64}}} \right)}^C}{{\left( {1 - {\text{BS}}\& \text{W}\% } \right)}^D}}}{{A{{\left( {{\text{GLR}}} \right)}^B}}}$$
(3)

\({y_i}\) = measured liquid flow rate QL(measured). \({\hat {y}_i}\) = predicted liquid flow rate QL(predicted). n number of data records sampled. A proportionality constant. B gas liquid ratio exponent. C = choke size exponent. D BS&W exponent.

The coefficients A, B, C, and D in Eq. (3) are the independent variables evaluated by the GA with Eq. (2) as its objective function.

A key control parameter for the GA (applied in step 8, Fig. 2) is a shrink factor applied (Eq. 4) as part of Gaussian mutation. This factor causes the standard deviation a Gaussian distribution supplying random numbers to progressively shrink as GA generations (iterations) advance

$${\sigma _{t+1}}={\sigma _t}\left( {1 - \frac{t}{m}} \right)$$
(4)

where \(\sigma\) is the standard deviation of the gaussian distribution applied for the mutation operator in that generation. t is a specific generation. t + 1 is the next generation. m is the total number of generations (iterations) specified for the GA. The impact of the shrink factor is to reduce the scale of change induced by mutation as generations progress toward convergence.

The control and behavioral parameters for the genetic algorithm are given in Table 1.

Table 1 Genetic algorithm control and behavioral parameters applied
Full size table

Excel’s Solver provides standard evolutionary and non-linear optimization

The Solver optimizer is a standard function in Microsoft’s Excel software and readily applied with options to select linear (simplex), non-linear (generalized reduced gradient, GRG) or evolutionary algorithms to apply. We compare the customized genetic algorithm developed for this study with the Solver options applying GRG and evolutionary algorithms to the same field dataset.

The Solver optimizer is easily set up for the flow prediction model by: (1) specifying a range of cells in a spreadsheet specifying the input data variable range; (2) specifying a range of cells in the spreadsheet specifying the constraints to place on the formula coefficient ranges to be tested; (3) specifying a single cell in the spreadsheet as the statistical precision variable to be minimized by Solver (i.e., the target cell and objective function), and (4) selecting which solver algorithm to apply (e.g. GRG or evolutionary in the context of the current model).

Restrictions on optimization applying Excel’s Solver are:

  1. 1.

    Only one objective function variable can be specified for each run of Excel’s Solver making it a single-dimensional optimizer. This is the way that Microsoft have configured the Solver algorithm in Excel so it cannot be used directly for multi-objective optimization This is not an issue for the flow-rate prediction model considered here because it is does have just one objective function (i.e., liquid flow rate).

  2. 2.

    These specified input variable range must be linked via formula(s) in the spreadsheet to the single-specified objective function.

  3. 3.

    It is important before running the optimizer to test, by some running deterministic cases, that the mathematical relationship between the specified input variables and the objective function is working appropriately. This involves defining cell formula(s) to define the flow-rate predictions for each data record (involving the unknown coefficient values applied to the formula) and the single statistical precision measure to be minimized as the objective function. It also involves testing the constraint ranges applied to the coefficients in the formula. If this is not done, there is a risk that the optimizer will not function as expected.

  4. 4.

    Excel’s Solver optimizer only provides a single (optimum) result, if it finds one. In some optimization problems, it is useful to retain and evaluate several high-performing solutions rather than just one. A customized evolutionary algorithm, such as the genetic algorithm applied in this study, can provide multiple high-ranking solutions, if required.

Analysis of Reshadat oil field data

In this study, 182 datasets were collected from 7 wells penetrating 3 distinct reservoir zones (#1, #2, and #3) that are located adjacent to one another in the Reshadat oil field. The Reshadat oil field is located 110 km south–west of Lavan Island. It was discovered in 1965 and first brought onstream in 1968. It has undergone a significant renovation and extended development since 2008 with five new platforms installed and many new wells drilled in recent years to increase oil production rates. Fluid properties of the three reservoir zones are shown in “Appendix 2” (training subset) and “Appendix 3” (testing subset).

All the collected data are divided randomly into two groups: 70% (127 datasets) were used for training; and, 30% for (55 datasets) for testing. The data include wellhead pressure, gas–liquid ratio, percentage of BS&W [base sediment and water, which incorporates produced water (free water), water in produced sediment/solids, and some water derived from emulsions with oil], choke size, and oil production rate. The ranges and mean values associated with each of these variables in the Reshadat field dataset are listed in Table 2; a full data listing is provided in “Appendix 2”.

Table 2 Distribution of variable values for the Reshadat oil field dataset
Full size table

Developing a new model for predicting liquid flow rates through wellhead chokes

Oil flow rate through a wellhead choke is a function of: (a) choke size; (b) wellhead pressure; (c) percentage of water produced (expressed as BS&W); and (d) gas–liquid ratio (Beiranvand et al. 2012), which are shown in the following equations:

$${Q_{{\text{L}}({\text{predicted}})}}={\text{ }}f{\text{ }}\left( {{P_{{\text{wh}}}},{\text{ }}{D_{64}},{\text{ BS}}\& \text{W},{\text{ GLR}}} \right)$$
(5)
$$X=\frac{{{P_{\text{wh}}} \times \left( {D_{64}} \right) \times \left( {1 - {\text{BS}}\& \text{W}\% } \right)}}{{\left( {\text{GLR}} \right)}}$$
(6)

where the units of these variables are: liquid production rate (QL) is measured in stock tank barrels (STB/D). Wellhead pressure (Pwh) is measured in pounds per square inch gauge (Psig). Choke size (D64) is measured in 1/64 in. Base sediment and water (BS&W) is measured as a percentage of liquid production. Gas–liquid ratio (GLR) is measured in Scf/STB.

To analyze the X function and find the best relationship between parameters, BS&W, D64, GLR, and Pwh to predict QL(predicted) accurately, QL(measured) is evaluated versus the calculated value of X (Eq. 6) for each dataset record (Fig. 3). The QL versus X cross plot for the Reshadat field dataset (Fig. 3) reveals a correlation coefficient of 0.8901 between these parameters, indicating a good positive correlation with the equation for the best-fit straight line through the data shown in the equation below:

Fig. 3
figure 3

Liquid production rate QL(measured) versus parameter X calculated with Eq. (6) displaying the best-fit straight line (Eq. 7) and correlation coefficient

Full size image
$$X{\text{ }}={\text{ }}0.0184{\text{ }}{Q_{{\text{L}}({\text{measured}})}} - {\text{ }}8.027$$
(7)

The accuracy of the prediction of liquid flow rate [QL(predicted)] can be improved by adding coefficients A, B, C, and D to Eq. (6) to form the expression forming part of the GA fitness test. This relationship (repeated as Eq. 8) enables various values of A, B, C, and D to be applied to it to test the accuracy of the predicted versus measured values of QL for each record in the dataset

$${Q_{{\text{L}}({\text{predicted}})}}=\frac{{{P_{\text{wh}}}{{\left( {D_{64}} \right)}^C}{{\left( {1 - {\text{BS}}\& \text{W}\% } \right)}^D}}}{{A{{\left( {{\text{GLR}}} \right)}^B}}}$$
(8)

The GA applied uses Eq. (8) as part of its objective function to minimize the fitness function to rapidly find optimum values for coefficients A, B, C, and D that minimize the error between QL(predicted) and measured QL(measured) for the entire dataset. The GA objective function is essentially a mean-square-error (MSE) function and can be expressed in expanded form as the following equations:

$${\text{Fitness}}(f)={\text{MSE}}=\frac{1}{n}\mathop \sum \limits_{{i=1}}^{n} {\left( {{{({Q_{\text{L}}})}_{{\text{Measured}}}}_{i} - {{({Q_{\text{L}}})}_{{\text{Predicted}}}}_{i}} \right)^2}$$
(9)
$${\text{Fitness}}\left( f \right)=\frac{1}{n}\mathop \sum \limits_{{i=1}}^{n} {\left( {{{({Q_{\text{L}}})}_{{\text{Measured}}}}_{i} - {{\left( {\frac{{{P_{{\text{wh}}}}{{\left( {{D_{64}}} \right)}^C}{{\left( {1 - {\text{BS}}\& \text{W}\% } \right)}^D}}}{{A{{\left( {{\text{GLR}}} \right)}^B}}}} \right)}_i}} \right)^2}$$
(10)

where QL(predicted) = predicted liquid production rate. QL(measured) = measured liquid production rate. n = number of data records sampled.

To establish appropriate control and behavioral parameters for the GA that speed its convergence toward acceptable and repeatable minima for the fitness function f (Eq. 10), it is necessary to run a series of trials applying different values to these parameters. Each problem and dataset have their own particular characteristics, which mean that GA control parameter values and methods that work well for one dataset may be sub-optimal for another. For the Reshadat field dataset, trials led to the selection of the GA control and behavioral parameters and the GA selection, crossover, and mutation methods as listed in Table 1. Applying those values to the GA, it was then used to determine the optimum values for the A, B, C, and D coefficients to use in Eq. (8), by minimizing fitness function f for the 70% of the dataset records allocated for training. Exactly, the same approach was used when applying Excel’s Solver optimizers (GRG and evolutionary) to the Reshadat field dataset.

Statistical measures used to measure the accuracy of optimum solutions

Once the GA, by minimizing the fitness function, has selected optimum values for coefficients A, B, C, and D to apply in Eq. (8), it is necessary to establish the accuracy with which Eq. (8) can match QL(predicted) values with QL(measured) values for each record the test section of the dataset (i.e., the 30% of the entire Reshadat field data records selected randomly to form the test subset).

The following six statistical error measures for accuracy, precision, and correlation (expressed as Eqs. 11 to 17) were calculated for the optimum solution values for coefficients A, B, C, and D (Eq. 8) applied to the test subset with results shown in Table 3.

Table 3 Optimum values for coefficients A, B, C, and D applied to Eqs. 6 and 8 and other published liquid flow prediction (Eq. 19) for wellhead choke relationships
Full size table

Percent deviation for dataset record i (PDi):

$${\text{P}}{{\text{D}}_i}=\frac{{{Q_{{\text{L(Measured)}}}} - {Q_{{\text{L(Predicted)}}}}}}{{{Q_{{\text{L(Measured)}}}}}} \times ~100$$
(11)

Average percent deviation (APD):

$${\text{APD}}=\frac{{\mathop \sum \nolimits_{{i=1}}^{n} {\text{P}}{{\text{D}}_i}}}{n}$$
(12)

Absolute average percent deviation (AAPD):

$${\text{AAPD}}=\frac{{\mathop \sum \nolimits_{{i=1}}^{n} \left| {{\text{P}}{{\text{D}}_i}} \right|}}{n}$$
(13)

Standard deviation (SD):

$${\text{SD}}=\sqrt {\frac{{\mathop \sum \nolimits_{{i=1}}^{n} {{({D_i} - {\text{Dimean}})}^2}}}{{n - 1}}}$$
(14)

where Di is QLi(measured) – QLi(predicted) for each dataset record i. Dimean is the mean of the Di values

$${\text{Dimean}}=\frac{1}{n}\mathop \sum \limits_{{i=1}}^{n} \left( {{{({Q_{\text{L}}})}_{{\text{Measured}}}}_{i} - {{({Q_{\text{L}}})}_{{\text{Predicted}}}}_{i}} \right)$$

Mean square error (MSE):

$${\text{MSE}}=\frac{1}{n}\mathop \sum \limits_{{i=1}}^{n} {\left( {{{({Q_{\text{L}}})}_{{\text{Measured}}}}_{i} - {{({Q_{\text{L}}})}_{{\text{Predicted}}}}_{i}} \right)^2}$$
(15)

Also used for the GA fitness function f (Eqs. 7 and 8).

Root-mean-square error (RMSE):

$${\text{RMSE}}=\sqrt {{\text{MSE}}}$$
(16)

Coefficient of determination (R2):

$${R^2}=1 - \frac{{\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{Q_{{\text{L(Predicted)}}}} - {Q_{{\text{L(Measured)}}}}} \right)}^2}}}{{\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{Q_{{\text{L}}\left( {{\text{Predicted}}} \right)}} - \frac{{\mathop \sum \nolimits_{{I=1}}^{n} {Q_{{\text{L}}\left( {{\text{Measured}}} \right)}}}}{n}} \right)}^2}}}$$
(17)

The statistical measures (Eqs. 11–17) are also reported in Table 3 for our GA evaluations, using the same method described for our proposed Eq. (8), of the liquid flow-rate prediction equations proposed and historically published by Gilbert (1954), Baxendell (1958), Ros (1960), and Achong (1961) (shown here as Eq. 19 with different values for coefficients A, B, and C) applied to the Reshadat field dataset.

Re-arranging Gilbert’s formula (Eq. 1) to predict liquid flow rate, and renaming the coefficients as A, B, and C to match those coefficients expressed in Eq. (8) provides the equation below:

$$Q=\frac{{{P_{{\text{wh}}}}{S^B}}}{{{\text{A}}{{\text{R}}^C}}}$$
(18)

Using the same symbols for the variables as Eq. (5), Gilbert’s formula for predicting flow (Eq. 18) can be expressed as Eq. (19). This omits the BS&W term (not considered by Gilbert) from Eq. (8) [which is the same as applying a value of zero to exponent D in (Eq. 8)]. The correlations derived by Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) involve different values for the coefficients A, B, and C applied to the following equation (Table 3):

$${Q_{{\text{L(predicted)}}}}=\frac{{{P_{{\text{wh}}}}{{\left( {{D_{64}}} \right)}^C}}}{{A{{\left( {{\text{GLR}}} \right)}^B}}}$$
(19)

where Gilbert (1954) derived values of coefficients A = 10; B = 0.546; C = 1.84; Baxendell (1958) correlation involves values of coefficients A = 9.56; B = 0.546; C = 1.93; Ros (1960) correlation involves values of coefficients A = 17.4; B = 0.5; C = 2.00; Achong (1961) correlation involves values of coefficients A = 3.82; B = 0.65; C = 1.88; Mirzaei-Paiaman and Salavati (2013) correlation involves values of coefficients A = 11.41; B = 0.553; C = 1.92; BS&W coefficient D = 0 in all five of the above cases.

Beiranvand et al. (2012) correlation involves values of coefficients A = 26.17; B = 0.5154; C = 2.151; D = 0.5297.

Table 3 reveals the significant superiority of our proposed Eq. (8), in terms of accuracy, compared to the other liquid flow-rate prediction formulas evaluated. APD, AAPD, SD, MSE, and RMSE values are all much lower for optimization of the Reshadat oil field dataset than for the other published formulas applying Eq. (19). All formulas evaluated show high correlation coefficients (≫ 0.9 or 90%), which is hardly surprising as Eq. (6) (with A, B, C, and D coefficients all equal to 1) achieves a correlation coefficient of 0.89 (89%). However, the high correlation coefficients reveal little about accuracy of the predictions [i.e., QL(predicted) versus QL(measured)]. As can be seen from Fig. 3 and Table 3, the values of X calculated by Eq. (6) include orders of magnitude of error in relation to QL(measured). Although the Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) formulas also significantly outperform Eq. (6) in terms of accuracy, their levels of accuracy (i.e., APD, AAPD, SD, MSE, and RMSE values) they are much inferior in accuracy to those achieved by our proposed Eq. (8) and the Solver (GRG and evolutionary) solutions (Table 3).

Figures 4 and 5 show a comparison of QL(predicted) versus QL(measured) for each data point training subset (127 randomly selected data records) and testing subset (55 randomly selected data records), respectively, of the Reshadat oil field dataset (total of 182 wellhead test data records).

Figures 4 and 5 show excellent agreement between QL(predicted) versus QL(measured) for both training and testing datasets using Eq. (8), which is confirmed by Fig. 6.

Fig. 4
figure 4

Liquid flow-rate (QL) prediction reliability and accuracy for the Reshadat oil field training data subset applying the GA optimized Eq. (8)

Full size image
Fig. 5
figure 5

Liquid flow-rate (QL) prediction reliability and accuracy for the Reshadat oil field testing data subset applying the GA optimized Eq. (8)

Full size image
Fig. 6
figure 6

Liquid flow rate QL(predicted) versus QL(measured) reveals a strong correlation and high reliability and accuracy for the Reshadat oil field applying the GA optimized Eq. (8) to the test data subset (55 data records)

Full size image

Figure 7 demonstrates the ability of the GA optimization method to transform the highly inaccurate functional relationship expressed as Eq. (6) into the highly accurate prediction formula expressed as Eq. (8).

Fig. 7
figure 7

Liquid flow rate QL(predicted) versus QL(measured) reveals a strong correlation for the Reshadat oil field applying Eq. (6) and the GA optimized Eq. (6) to the test data subset (55 data records). However, Eq. (6) provides highly unreliable and inaccurate predictions in comparison to Eq. (8)

Full size image

Performance comparisons with published correlations

Figure 8 compares the relative performance for the Reshadat oil field dataset of applying Eq. (19) with the A, B, C, and D (where appropriate) coefficient values of Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), Mirzaei-Paiaman and Salavati (2013) and Excel Solver (GRG and evolutionary). All show good correlations (coefficient of determination ≥ 0.93) between measured and predicted liquid flow rates, but not very impressive accuracy (Table 3). However, the performance of all of published correlations are substantially inferior in terms of accuracy to Eq. (8) (GA solution) and the two Solver solutions, as measured by a range of statistical metrics (Table 3).

Fig. 8
figure 8

Liquid flow rate QL(predicted) versus QL(measured) achieved by applying the two Excel Solver optimization algorithms (non-linear and evolutionary) and the published liquid flow-rate prediction formulas of Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) to the Reshadat oil field applying Eq. (19) with appropriate coefficients to the test data subset (55 data records)

Full size image

Figures 9 and 10 show the percent deviation (PDi) for each data record in the test data subset applying the GA optimization algorithm to Eqs. (6) and (8) (Fig. 9) and with various coefficient values from published studies and Solver algorithms applied to Eq. (19) (Fig. 10) for predicting liquid flow rate. The PDi measure is useful in revealing where in the production rate range significant errors occur. In the case of Eq. (6), high errors occur across the entire production rate range of the dataset. In the case of Eq. (8), significant errors (beyond the plus or minus 20% range) only occur in the prediction of flow rates in four data records with flow rates below 3000 STB/D (see Figs. 5, 9). This is not surprising as higher percentage errors are much more likely to be calculated using Eq. (11) for low rate tests. What is encouraging for Eq. (8) is that so few data records suffer from such high PDi errors, even among the data records with low measured flow rates.

Fig. 9
figure 9

Percent deviation (PDi) calculated by Eq. (11) for the Reshadat oil field applying Eq. (6) and the GA optimized Eq. (8) to the test data subset (55 data records). Equation (6) displays very high PDi values (reflecting high prediction errors), whereas Eq. (8) displays very low PDi values (reflecting low prediction errors)

Full size image
Fig. 10
figure 10

Percent deviation (PDi) calculated by Eq. (11) for the Reshadat oil field applying various coefficients to Eq. (19) for the published liquid flow-rate prediction formulas of Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) to the test data subset (55 data records). The Achong (1961) formula displays lower PDi values than the other published formulas (reflecting lower prediction errors), but these are higher than for our Eq. (8) (Fig. 9)

Full size image

In contrast to Fig. 9, the PDi result comparisons for the published Eq. (19) applying A, B, C, and D (where appropriate) coefficient values of Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) plotted in Fig. 10. These reveal, for these published correlations, predictions of multiple records with flow rates less than 3000 STB/D display PDi values of less than minus 50%. This suggests that these formulas are systematically over-estimating liquid flow-rate predictions for the lower flow-rate data records. On the other hand, Gilbert, Baxendell, and Ros formulas are all under-estimating liquid flow-rate predictions for the higher flow-rate data records (> 5000 STB/D). The Gilbert formula performs the worst for this dataset by under-estimating liquid flow-rate predictions for flow rates > 3000 STB/D to a progressively higher degree from about 25% at 5000 STB/D to > 50% at 30,000 STB/D. Figure 10 reveals that for flow rates above 3000 STB/D, the Achong formula performs the best of these published formulas with low (negative) PDi errors but performs the worst at flow rates < 3000 STB/D, particularly when compared to the Excel Solver (GRG and evolutionary) solutions.

Figures 11, 12, and 13 confirm the superior performance in terms of statistical accuracy of Eq. (8) optimized with evolutionary and/or non-linear algorithms compared to the other formula published for predicting liquid flow rate from wellhead test data records for the Reshadat oil field dataset.

Fig. 11
figure 11

A comparison between root-mean-square error (RMSE) and absolute average percent deviation (AAPD%) for the Reshadat oil field applying GA and Solver optimization to Eqs. (6), (8), and (19) for the published liquid flow-rate prediction formulas proposed by this study and by Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), Beiranvand et al. (2012), and Mirzaei-Paiaman and Salavati (2013) to the test data subset (55 data records)

Full size image
Fig. 12
figure 12

A comparison between root-mean-square error (RMSE, Eq. 16) and absolute average percent deviation (AAPD%, Eq. 13) for the Reshadat oil field for the various flow-rate prediction methods identified in Fig. 11

Full size image
Fig. 13
figure 13

A comparison between mean square error (MSE, Eq. 15) and coefficient of determination (R2, Eq. 17) for the Reshadat oil field for the various flow-rate prediction methods identified in Fig. 11

Full size image

Discussion

The analysis presented for flow-rate prediction for the Reshadat field dataset indicate that both evolutionary and non-linear optimization algorithms can provide highly accurate results by applying the proposed methodology. Although there is almost negligible difference between the level of accuracy achieved by the customized genetic algorithm (GA) and Excel Solver’s GRG and evolutionary optimizers methods is the same approximately, the Solver optimizers display slightly higher levels of accuracy. The preciseness of the GA is shown to be fit for purpose acceptable but is slightly outperformed by the Solver solutions.

We consider the main reason for this slight difference between GA and the Solver solutions is due to the several behavioral and control setting parameters associated with the GA (Table 1). The developed GA requires that values have to be selected for the behavioral and control setting, including: initial population, crossover percent, the number of elites, migrated population, selection method, and crossover method. The values for these metrics are usually determined by trial and error or tuned to a specific dataset. This can be time consuming and mean that when applied to a slightly different set of data, slightly higher errors are incurred in the prediction (e.g., tuning the control metrics for the training data subset and then applying them to the testing data subset). One advantage of the Solver optimizers is that they can be setup and applied rapidly avoiding the need to tune any behavioral or control metrics.

The methodology has the potential to add additional relevant variables, if required. We have not considered additional variables, such as fluid temperature, because other studies have suggested that additional variables to those considered have very small impacts on liquid flow rates from oil reservoir production or well tests. For instance, Choubineh et al. (2017a, b) concluded that the effects of temperature on liquid flow rate is not remarkable. Furthermore, sensitivity analysis performed on the Reshadat field dataset suggests that it is best not to include fluid temperature in the liquid flow-rate performance model. Relevancy factor (r) as defined by Choubineh et al. (2017a, b) was calculated using Eq. (20) to investigate the dependence of the liquid flow rate on fluid temperature. The r value calculated is 0.11 that shows it does not have any significant effect on liquid flow rate

$$r=\frac{{\mathop \sum \nolimits_{{i=1}}^{N} \left( {{T_i} - {T_{{\text{ave}}}}} \right)\left( {{Q_i} - {Q_{{\text{ave}}}}} \right)}}{{\sqrt {\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{T_i} - {T_{{\text{ave}}}}} \right)}^2}\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{Q_i} - {Q_{{\text{ave}}}}} \right)}^2}} ~~}}$$
(20)

where \({T_i}\) is the ith fluid temperature input value; \({T_{{\text{ave}}}}\) is the average fluid temperature of all data records; \({Q_i}\) is the ith value of liquid flow rate; \({Q_{{\text{ave}}}}\) is the average value of liquid flow rate; and, N is the number of all data records in the dataset.

The QA and Solver algorithms presented are configured as single-objective optimization calculations. It is possible to expand these algorithms as multi-objective algorithms by using a function test based on assigning a score to each of the statistical measures of accuracy identified in “Statistical measures used to measure the accuracy of optimum solutions”. The multi-objective optimization algorithms are then configured to maximize the combined function test score. This approach is deemed unnecessary for the Reshadat field dataset, because the GA and Solver algorithms achieve acceptable levels of accuracy configured to minimize MSE. However, in datasets where a single-objective statistical measure does not achieve sufficient levels of accuracy between predicted and measured liquid flow rates, applying a multi-objective algorithm configured as described is likely to improve that accuracy.

Conclusions

A new liquid flow-rate prediction model based on 182 collected data records of well tests through production chokes from seven wells drilled in the Reshadat oil field, offshore Southwest Iran, is developed and evaluated. The novel liquid flow-rate-prediction formula employed (Eq. 8) involves four independent variables and when optimized with either a customized genetic algorithm or Excel’s Solver optimizers demonstrates high accuracy in predicting flow rate for the Reshadat oil field data. For the genetic algorithm it achieves the following values for statistical accuracy measures: average percent deviation = − 2.89%; absolute average percent deviation = 7.33%; standard deviation = 563.85; mean squared error = 316,429; root-mean-square error = 562.52; and coefficient of determination = 0.9970.

The optimization methodology applied divided the dataset into training and testing subsets and minimizes as the objective function the mean square error between measured and predicted flow rates. This approach is easy and flexible to setup train and test and is readily adaptable for application to other well-test datasets.

The two Solver algorithms achieved lower MSE values than the GA algorithm, with the Solver evolutionary algorithm achieving the lowest MSE value of 91,871. This confirms that both non-linear and evolutionary optimization algorithms are almost equally effective when applied with the proposed methodology to the Reshadat field dataset. Applying Eq. (8) with optimized values for its coefficients derived from non-linear and evolutionary algorithms, fine-tuned for specific field data, should enable production engineers to significantly improve their flow-rate predictions for this field compared to other methods.