Introduction

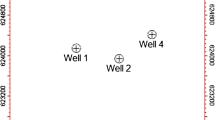
The Chanda oil field in Khyber Pakhtunkhwa, Pakistan, marks the first advent of an era of hydrocarbon exploration in the province since its discovery in 1998–1999. Located in the Shakardara area of the Kohat District, the field is known to provide 34.57 million U.S. barrels of original recoverable oil reserves by 0.6888 trillion cubic feet, and original recoverable reserves of associated gas (June 2012 estimated figures, Pakistan Energy Yearbook (2012). The study area lies between 33°–34°N and 71°–72°E. The Chanda oil field includes Chanda-1, Chanda-2, Chanda-3, and Chanda Deep-1, all of which are producing based on extractions from the Datta and Kingriali Formations. The main producing reservoir in the Chanda oil field is the Datta Formation, which is encountered in several other wells in the Kohat–Potwar region, including Manzalai, Makori East, Sumari Deep-1, Marwat-1, Pezu-1, Toot-1, and Dhulian. Figure 1 shows the location of the wells used in the present study.

Fig. 1
figure 1

a Structural map of the Kohat Plateau, northern Pakistan (modified after Khan et al. 1986; Gee 1989). The inset shows the location of the study area. b Basemap showing location of wells used in the study and the correlation of two wells marking the presence of the Datta sands

Full size image

Various researchers have described the stratigraphy, structural styles, tectonics, and geophysical physiognomies of the Kohat region in northwest Pakistan (Fatmi 1973; Wells 1984; Khan et al. 1986; McDougall 1988; McDougall and Hussain 1991; Pivnik and Sercombe 1993; Sercombe et al. 1998; Wandrey et al. 2004). In this study, an approach of integrating petrophysics with the Gassmann fluid substitution was applied on the Datta sands of the Chanda oil field, northwest Pakistan, for field development and reservoir characterization. The overall objective of this work was to apply several rock physics diagnostic methods to examine porosity, saturation, shale volume (net-to-gross), cementation, and pore fluid discrimination of Jurassic reservoir rocks in the Chanda oil field discovery, with special emphasis given to the Datta Formation, the main reservoir in the area. In addition, the effects of water saturation on the seismic properties of the rocks were examined to provide information for mitigating the risk of development well failure in the area. Integrating petrophysics with rock physics provides the information required to understand and connect various geophysical datasets delineating the intrinsic properties of rocks, such as mineralogy, porosity, pore shapes, and pore fluids. This integrated approach increases the quality and makes it easy to recapitulate as much as needed to achieve the best match with all the data. The results derived from the integration of data lessen risk, improve method efficiency, boost overall production, and increase the return rate of economic assets.

Tectonic setting of the area

The Northwest Himalayan Fold and Thrust Belt comprised the mountain ranges of Nanga Parbat, Hazara, southern Kohistan, Swat, Margalla, Kala Chitta, Kohat, Sufaid Koh, the Salt Range, and its western extension (Kazmi and Jan 1997). Pivnik and Wells (1996) indicated that the Panjal–Khairabad Thrust Fault is a division between the northwest Himalayan zone (Foreland) and deformed and metamorphosed northern zone (Hinterland). The hinterland is the Himalayan crystalline nappe and thrust belt, while the foreland comprises the Hazara Kashmir Syntaxis, Salt Range, Kohat–Potwar Fold Belt, and the Kurram–Cherat–Margalla Thrust Belt (Fig. 1B).

The northern region of the Kohat plateau is marked by tight, often overturned folds, out-of-syncline faults, and several thrust faults. Some of the low-angle thrust faults have been folded and form klippe. These constitute a distinct thrust belt referred to as the Mir Khwali Sar Trust Belt (MKSTB) which, according to Pivnik and Sercombe (1993), is a compression-related, relict, thin-skinned thrust belt. Few faults exist outside MKSTB because the Eocene Panoba Shales serve as a detachment horizon in which faults flatten near the surface and are not exposed. East–west folds, and north and south dipping reverse faults are common in the southern part of the Kohat plateau. Bahadurkhel Salt is exposed in the anticlinal cores, while Jatta Gypsum is commonly imbricated and folded with slivers of Panoba Shale. Pivnik and Sercombe (1993) indicated that lower Eocene rocks were thrust over Miocene molasses at several places. The structures have an east–west orientation north of Shakardara; however, near Shakardara, the structures change orientation abruptly from east–west to north–south. A large thrust fault called Hukni Fault traverses the area. This fault is located above a north–south lateral ramp, in the basement, and the swing in a strike near Shakardara records a progressive fading away of the lateral and frontal ramp complex at depth (Abbasi and McElroy 1991).

The Surghar, Marwat, Khisor, Pezu and Manzai ranges in the southern Kohat plateau, collectively referred to as the Trans Indus Ranges, surround the Bannu depression. The Surghar and Khisor ranges are asymmetrical, over-folded anticlines with Permian strata exposed in the core and overlain by Mesozoic and Paleogene rocks (Kazmi and Jan 1997). In contrast, the Marwat range is an anticlinal feature covered largely by Siwaliks. Similarly, Bhittani and Manzalai are also anticlinal features with Siwalik cover. The north dipping Surghar Thrust is located along the western margin of the Surghar Range. According to Gee (1989), this is most likely a western extension of the Salt Range Thrust, and thus continues along the southeastern margin of the Trans-Indus Ranges. Figure 2 shows the detailed stratigraphy of Kohat Basin.

Fig. 2
figure 2

Generalized stratigraphy of Kohat Basin

Full size image

Dataset and methodology

This study was carried out using well data from Chanda-1, and Chanda Deep-1. The well logs were used to calculate petrophysical parameters, including shale volume, porosity, permeability, and water saturation. Cross plots were produced to provide a quick view of the lithological information (sand-shale content) of the reservoir. The log data available for both wells included gamma ray (GR), spontaneous potential (SP), density (RHOB), neutron porosity (NPHI), resistivity (MSFL, LLS, LLD) and NGS logs (URAN, THOR, POTA). The evaluated petrophysical properties, shown in Table 1, include gross thickness (GROSS), net thickness (NET), net-gross ratio (NGR), porosity (PHA), permeability (K), and water saturation (SW). The net reservoir thickness was calculated from the following equation:

Table 1 Petrophysical parameters (gross thickness, net thickness, net-gross ratio and average porosity, water saturation and mean permeability) calculated for the Datta sands using log data from two wells
Full size table
$$\frac{{{\text{Net}}}}{{{\text{Gross}}}}=\frac{h}{H},$$
(1)

where H is the gross thickness of the formation and h is the shale intervals within the formation.

Shaley sands in reservoirs can be estimated by calculating the volume of shale in the sand (Asquith 1982). A shale volume estimation (VSh) was performed using the values from the GR log with the following equation:

$${V_{{\text{Sh}}}}=\frac{{{\text{G}}{{\text{R}}_{{\text{log}}}} - {\text{G}}{{\text{R}}_{{\text{min}}}}}}{{{\text{G}}{{\text{R}}_{{\text{max}}}} - {\text{G}}{{\text{R}}_{{\text{min}}}}}},$$
(2)

where GRlog is the chosen log value, and GRmin and GRmax are the values chosen for the sand and shale baselines. The following equations were used for porosity determination:

$${\text{PHID}}=\frac{{{\text{Rhoma}} - {\text{Rhob}}}}{{{\text{Rhoma}} - {\text{Rhof}}}},$$
(3)
$${\text{PHIT}}=\frac{{{\text{PHID}}+{\text{NPHI}}}}{{2.0}}~~,$$
(4)

where Rhof (ρf) is 1.0, and Rhoma (ρmatrix) is 2.65 for sandstones. Rhob is the bulk density log, PHIT is the total porosity, PHID is the density porosity, and NPHI is the neutron porosity. The Archie equation (Archie 1942)  was used to estimate the saturation of the reservoir (Jackson et al. 2007), expressed as:

$$~~~~{S_{\text{w}}}=\left[ {\frac{{a \times {R_{\text{w}}}}}{{{R_{\text{t}}} \times }}{\phi ^m}} \right]1/n,$$
(5)

where SW is the water saturation, a is the tortuosity factor (varies from 0.5 to 1.5 in different reservoirs), Rw is the formation water resistivity, m is the cementation exponent 1.8–2.0 (varies in clastic rocks), φ is the porosity, and n is the saturation exponent (with a value of 2). The Winsauer equation is generally used for evaluation of sandstone using resistivity logs. The unmodified Archie formula (Archie 1942) with a = 1.0 and m = 2.0 is often used for carbonates. The Winsauer equation was developed in a study by Winsauer et al. (1952) of the formation factor, versus the porosity relationship of many different types of sandstone. Based on the studied rocks, they produced the following expression:

$$~F=\frac{a}{{{{\left( {{\text{PHIE}}} \right)}^m}}},$$
(6)
$${R_{\text{o}}}=F \times {R_{\text{w}}}.$$
(7)

The resistivity of formation water (Rw) can be obtained by the analysis of water samples from a drill stem test (DST), in a water-producing well, using a catalog of water resistivity values calculated from the SP log using the Schlumberger chart book (Schlumberger 1989). Rw from a resistivity–porosity log is found by the calculation of the Rwa log as follows:

$${R_{{\text{wa}}}}=\frac{{{R_{\text{t}}}}}{F},$$
(8)

where Rt is from the deep investigation resistivity log, and F is from the porosity log reading. The Gassmann fluid substitution analysis was used to model the seismic velocities of the rock, and the effects of fluid on the rock. The Gassmann equation (Gassmann 1951) determines the effects of pore fluids on wave propagation speed. This analysis substitutes fluids with known properties, such as gas, oil, or water, for the original pore contents, replacing the wave speeds in the formation with those of the substituted fluids. The results indicated that the P-wave velocity and P-impedance decreased with an increase in hydrocarbon saturation. This behavior was confirmed by the petrophysical analysis of the log data. Pore fluids have the ability to change several rock properties (Vp, Vs, and density) and seismic properties. Shear sonic measurements were not available for the wells used in this study, therefore, the shear wave velocities for the two wells were calculated using the Greenberg and Castagna (1992) relationship. The resulting sonic shear (DTs) output curve was calculated by computing the equivalent velocities for all the pre-defined minerals. The fluid substitution segment of the analysis restores the log responses to those resulting from the original reservoir fluids at their original saturations. The fluid density, bulk modulus, and velocity can be calculated using the method of Batzle and Wang (1992). Similarly, the mineral properties, including the quartz and clay parameters were taken from Mavko et al. (2009). Parameters such as the bulk modulus (K), shear modulus (G), and bulk density \(({\rho _{\text{b}}})\) were derived using the following equations:

$$K={\rho _{\text{b}}}\left( {{V_{\text{p}}}^2 - \frac{4}{3}{V_{\text{s}}}^{2}} \right),$$
(9)
$$G={\rho _{\text{b}}}{V_{\text{s}}}^{2}~,$$
(10)
$${\rho _{\text{b}}}={\rho _{\text{o}}}\left( {1 - \phi } \right)+{\rho _{{f_{1~}}}}\phi ~,$$
(11)

where ρo is the matrix density = 2. 65, ρf is 1.0, and \(\phi ~\) is 7% or 0.07. The rock bulk modulus was calculated using the following expression:

$${K_{{\text{sat}}}}=\frac{{{K^*}~\left( {1 - \frac{{{K^*}}}{{{K_{\text{o}}}}}} \right)2}}{{\frac{\phi }{{{K_{{\text{fl}}}}}}+\frac{1}{{{K_{\text{o}}}}} - \frac{{\phi - K*}}{{{K_{\text{o}}}^{2}}}}}.$$
(12)

To define the frame rock properties or the dry rock bulk modulus (K*), the following expression was used:

$${K^*}=\frac{{{K_{{\text{sat}}}}\frac{{\left( {\phi {K_{\text{o}}}+1 - \phi } \right)}}{{{K_{{\text{fl}}}}}} - {K_{\text{o}}}}}{{\frac{{\phi {K_{\text{o}}}}}{{{K_{{\text{fl}}}}}}+\frac{{{K_{{\text{sat}}}}~1 - \phi }}{{{K_{\text{o}}}}}}}.$$
(13)

The shear modulus, matrix bulk modulus, and porosity remain constant. After obtaining the value of K*, it is possible to calculate the saturated rock bulk modulus (Ksat), using the above equation, for any water saturation values, recalculating Kfl, ρfl and ρb each time (Smith et al. 2003). The shear modulus being insensitive to fluid changes will remain constant during the substitution (Smith et al. 2003). The bulk density will change depending on the fluid saturation during the substitution. Gassmann relationships generally reflect the changes in P-wave and S-wave velocities due to saturation changes with simple inputs. The initial inputs for this study were the density and P-wave velocity logs, and the constant parameters during substitution were the matrix bulk modulus (Ko), frame or dry rock bulk modulus (K*), porosity (φ) and rock shear modulus (G; Smith et al. 2003). Three saturation models (brine, oil, and gas) were calculated and used to understand the sensitivity of the saturation of different sandstones.

Results and discussion

A discussion of the results is presented in three distinct sections including well log analysis, log interpretation of clastic reservoirs, and Gassmann fluid substitution.

Well log analysis and cross-plots

The gross thickness of the Chanda-1, and Chanda Deep-1 wells was determined using the tops and bases of the reservoir sands across the wells (Table 1). The net thickness is the thickness of the reservoir, which was determined by defining the non-reservoir and reservoir intervals of sands, based on the baseline. For this purpose, a shale baseline and a sand baseline were drawn using an appropriate cut-off. The thickness of shale within the reservoir sands was obtained, and that value was subtracted from the gross thickness. The reservoir zone 1 of Chanda-01 well shows the following petrophysical characteristics: gross: 21, net: 21, NGR: 1.00, PHA: 0.07, and SW: 0.29 (Fig. 3). The calculated petrophysical parameters for each reservoir zone of Chanda Deep-01 are: zone 1 (gross: 10, net: 9.50, NGR: 0.95, PHA: 0.06, SW: 0.79), zone 2 (gross:3, net: 2.50, NGR: 0.83, PHA: 0.05, SW: 0.61), zone 3 (gross:13, net:7.88, NGR: 0.61, PHA: 0.05, SW: 0.63) and zone 4 (gross: 5, net: 4.50, NGR: 0.90, PHA: 0.05, SW: 0.67) (Fig. 4). We observe a variation in NGS values and argillaceous content between two wells. Such variation in facies, reservoir quality and sand body architecture is likely possible as noted from previous investigators stating that variability is high in deltaic systems with highest variability occurring in fluvial-dominated deltas (Cleveland and Molina 1990).

Fig. 3
figure 3

Wireline logs of Chanda-1 showing various log characteristics in the Datta sands. Shale volume (VSh), density porosity (PHID), total porosity (PHIT) and water saturation (SW) are shown calculated in software. NGS logs showing the concentration of thorium, potassium and uranium in the Datta sands of Chanda-1 well. Badhole corrections were applied to logs using Schlumberger corrections (2000)

Full size image
Fig. 4
figure 4

Wireline logs of Chanda Deep-1 showing various log characteristics in the Datta sands. Shale volume (VSh), density porosity (PHID), total porosity (PHIT) and water saturation (SW) are shown. NGS logs show the concentration of thorium, potassium, and uranium in the Datta sands of Chanda Deep-1 well

Full size image

Pore fluid saturation in the sandstone reservoir is highly impacted by the heterogeneity and microstructure of sandstone. The net-to-gross (NGR) is one useful parameter for quantification of the heterogeneity of a sandstone reservoir. A reservoir zone could have a high NGR in a well log scale, and a low NGR on a seismic scale. A decrease in the NGR, results in an increase in the Vp/Vs, regardless of porosity. The NGR is higher in the Chanda Deep-1 in the east than it is in the Chanda-1 well in the west, indicating variations in the fractions of shale in the sandstone reservoir.

Cross-plots provide lithologic information for the Datta Formation (sand–shale content; Fig. 5). These cross-plots (GR vs. NPHI, NPHI vs. RHOB, GR vs. RHOB) provide a quick, qualitative view of the rock lithology contents. The hydrocarbon indication on the cross-plots is shown as either gas or light hydrocarbons that causes the porosity from the density log to increase (bulk density decreases) and the porosity from the neutron log to decrease (Schlumberger 1989). The GR vs. NPHI cross-plot (Fig. 5a, b) depicts variations in the lithology of the Chanda-1, and Chanda Deep-1 wells; the points with lower GR and NPHI values indicate sandstone, and the points with higher GR and NPHI values are indicative of shale. The GR vs. RHOB and NPHI vs. RHOB cross-plots (Fig. 5a–d) show the primary sandstone lithology.

Fig. 5
figure 5

Lithological identification cross-plots of the Datta clastics in Chanda-1 and Chanda Deep-1. a, b Cross-plot of GR vs. NPHI two wells. c, d Cross-plot of GR vs. RHOB. e, f Cross-plot of NPHI vs. RHOB

Full size image

Log interpretation of clastic reservoirs

The assessment of depositional environments is based on available GR wireline log data; however, core or sedimentological data is necessary for the accurate interpretation of a depositional environment because the defined gamma log trends are not indicative of a specific environment (Cant 1992; Siddiqui et al. 2013). The sandstone package in Chanda-1 represents a boxcar trend (Fig. 3). Fining upward signatures of the GR is evident in Chanda Deep-1, showing the irregular/ serrated signature of GR (Fig. 4). The left boxcar trend with less sharp edges occurs at intervals of 4710–4720, and 4790–4794 m in Chanda Deep-1. Based on petrophysical analyses, one hydrocarbon-bearing zone is identified in Chanda-1, while four such zones are identified in Chanda Deep-1 (Figs. 3, 4).

Gamma ray (GR) Log

The GR profile shows different shapes, including a block left boxcar and irregular trends (Figs. 3, 4). Boxcar log trends are typical of some types of fluvial channel sands, turbidites and, aeolian sands (Emery and Myers 1996). Irregular trends have no systematic change in either base line, and they lack the clean character of the boxcar trend; this represents an aggradation of a shaley or silty lithology, which may be typical of shelfal or deep water settings, and some lacustrine succession or muddy alluvial overbank facies (Cant 1992).

The Datta Formation trend in the GR logs is similar for the eastern and western wells, reflecting the same kind of paleo-depositional environment. Moreover, the gradual increase in the GR log’s response from the western part of the well to the eastern part seems to follow proximal to the distal paleo-environment settings. In the proximal zone (western well), due to the high energy environment, the deposited sediments are coarser than the sediments in the distal zone, where low energy prevails and causes inclusion of fine-grained sediments.

The natural gamma ray spectrometry (NGS) logs (Figs. 4, 5) represent the concentration of uranium (U), thorium (Th), and potassium (K) in a formation, where U and Th are expressed in parts per million (ppm) and K is expressed as a percentage (%). The concentration of these elements in the Chanda-1 and Chanda Deep-1 sands is shown in Fig. 6. The K content varies in the two wells; the level of K the sands in Chanda Deep-1 is high in comparison to Chanda-1. The Th content increases as the shale content in both wells vary, whereas the U content remains relatively constant.

Fig. 6
figure 6

Cross-plot of Th vs. K in Chanda-1 and Chanda Deep-1, indicating the concentration of thorium and potassium in clastics of the Datta Formation. The cross-plot shows concentrations of clay minerals montmorillonite, chlorite, and kaolinite

Full size image

Standard gamma ray (SGR) is the derived total GR log, which is the sum of all the radiation contributions, whereas computed gamma ray (CGR) is the computed GR log, which is the sum of the K and Th responses, excluding the U contribution. The NGS log is utilized to detect, identify, and evaluate radioactive minerals, thereby providing insight into the source depositional environment, diagenetic history and petrophysical characteristics of the rock, such as the surface area, and pore structure (Schlumberger 1989).

These logs are effectively used to differentiate among clay-bearing sandstone, arkose sandstone (high K content, low Th content), micaceous sandstone (low K composition, high Th composition), greywackes (equal amounts of Th and K), greensands (glauconite-rich), and heavy mineral bearing sandstones. The level of radioactive minerals in sandstone determines the content of the heavy minerals and clay, whereas K is usually contained in feldspars and micas. The high U concentration in shales suggests that shale is a source rock. High U with greater solubility and mobility is associated with fault planes, fractures, and formations where the flow has occurred. Since Th has a very low solubility and limited mobility, it is likely to accumulate with heavy minerals (Schlumberger 1989). High Th content is evident in Chanda Deep-1, coupled with GR at a depth of 4660–4680 m. High K content, coupled with a high GR response in a zone indicates that the rock could be micaceous sandstone. As shown in Fig. 6, the Th–K cross-plot indicates the separation of the Th and K in the Chanda-1 well; the high Th values and lower K values in the Chanda-1 well indicate micaceous sandstone, while in the Chanda Deep-1 well high K values indicate arkosic–feldspathic sandstone. We investigated the NGS log plots as an alternative to understand the depositional environments of sandstone types due to non-availability of drill well cuttings from studied wells.

Primmer et al. (1997) identified five diagenetic styles in sandstones including (1) quartz, with the presence of clays (e.g., kaolinite and/or illite), (2) clay minerals (illite or kaolinite), and (3) early diagenetic grain-coating clay mineral cements such as chlorite, which may inhibit quartz cementation during later burial. The quartz diagenetic style is most likely to occur in mineralogically mature sandstones (Primmer et al. 1997). Murray and Adams (1958) studied radioactivity of clastics and sandstone models of the changes in Th and U ratios and observed that the changes may suggest moving from a beach through shallow water and further to deep-water sediments.

The clay minerals (kaolinite, smectite, illite, chlorite, montmorillonite) analysis acts as a tool for environmental determination, stratigraphic correlation, and hydrocarbon generation zone (Weaver 1960). The cross-plots show the presence of clay minerals montmorillonite, chlorite and kaolinite in both wells with varying proportions. The high concentration of clay minerals is also related to high argillaceous content in Chanda Deep-1 well in comparison to Chanda-1. Weaver (1958) reported that even though no single clay mineral represents a particular environment, however, it may suggest a broad relationship of illite and montmorillonite to ancient marine rocks and kaolinite to continental rocks. Hampson et al. (2005) used the Th/K ratio to identify kaolinitic zones in a fluvial sequence of the Bookcliffs in Utah.

Arkosic sandstones generally suggest deposition in climatic regions which do not support weathering because they are either too dry or too cold. Another possibility of formation of arkose is where there is a crystalline source material rich in feldspar (such as granite or gneiss) and a high relief with consequent rapid erosion which gives no time to break up feldspar (Pettijohn et al. 1973). Arkosic sandstone occurs in association with alluvial fans and granitic mountain fronts in arid or semi-arid environments. Since feldspars are susceptible to chemical weathering in warmer and moist environments, clay minerals such as kaolinite are produced. The presence of arkosic type indicates deposition in a cooler, arid or semi-arid environment. This suggests a variability in fluvial-dominated deltaic depositional environment of Jurassic sandstone reservoirs from east to west in the area. Fluvial–deltaic sandstone deposits are proven to be good reservoirs in many other basins of the world (Olsen et al. 2017) as well as Jurassic deposits of fluvial–deltaic sedimentation (Shun-Li et al. 2014).

The Datta Formation is of early Jurassic age, and it is well developed in the Trans-Indus Ranges and the Salt Range (Dalnichik 1961; Dalnichik and Shah 1967). The formation consists of variegated sandstone, with shale, siltstone, and mudstone (Shah 1977). It extends as a tongue into Kala Chitta, Hazara and part of the Kohat area (Shah 1977). The Datta Formation has disconformable lower contact with the Kingriali Formation, and the upper contact with the Shinawri Formation is gradational. In the Kohat area, the formation is reported to be composed of quartzose, dolomitic, and oolitic limestone, suggesting a shallow marine shoreline with the development of a supratidal flat (Fatmi et al. 1990). The age is of Datta Formation is reported as early Jurassic (pre-Toarcian) (Shah 2009). The Jurassic system in Pakistan characterizes mainly limestones, shale, and sandstone. The lower part of the early Jurassic (Datta Formation) is composed of arenaceous and argillaceous sediments dominantly continental origin, grading upward in a sequence of marine calcareous/argillaceous rocks of Shinawri formation. The marine transgression in the Kohat–Potwar depositional basin is suggested to have occurred during late early Jurassic (Shah 2009). The siliciclastic sequence of Datta represents autocyclic sedimentation sequence caused due to environmental and depositional system fluctuations such as river avulsion, delta-lobe switching, and tidal channel migration.

Information on the depositional environment may be provided by the occurrence of certain common minerals. Detrital mica can be helpful in the diagnosis of depositional environments. Flakes of mica tend to be winnowed out of high energy environments due to turbulence and strong currents and carried away to be deposited in lower energy environments. Micaceous sands therefore tend to be absent from well-winnowed environments such as barrier islands, shallow shelf bars, and aeolian dunes. Settings in which micaceous sands characteristically occur include outer delta slopes, outer shelf, and submarine channels and fans.

Our findings from wireline logs interpretation confirm the previous findings, suggesting good reservoir potential of fluvio-deltaic succession/delta front facies. The presence of micaceous sandstone as inferred from the NGS logs also support the deltaic environment of Datta in the study area, as mica-rich sandstones are known to have been found in deltaic environments. Petrographic analysis by previous researchers has also reported the presence of kaolinite in Datta sandstones (Zaidi et al. 2013) which is in agreement with the results presented in this work. During the early Jurassic, the western margin of the Indian Plate was influenced by fluvial–deltaic settings along the regions characterizing Salt and Tran-Indus Ranges, showing a marked transformation to marine facies in the Hazara and Kohat areas (Meissner et al. 1975; Fatmi 1977).

During late Triassic–early Jurassic time, Mesozoic sediments were deposited along Tethyan platform characterizing the western margin of the Indian plate. The sea regression in the area resulted in the deposition of fluvio-deltaic sediments (Kazmi and Abbasi 2008) which includes the siliciclastic sequence of Datta Formation. The Early Jurassic was marked by the initial break-up of Gondwana and a subsequent marine transgression prevailed over the Horn of Africa depositing siliciclastics, carbonates, shale, marls, and evaporites (Coltorti et al. 2007; Abbate Ernesto et al. 2015). During early to middle Jurassic, the Indian Plate was part of Gondwana remnant characterizing warm temperate climatic conditions (Scotese 2001). Facies variation in Datta Formation in different parts of Upper Indus Basin such as Kohat–Potwar, Kalachitta, and Hazara regions have been reported by previous researchers (Kazmi and Abbasi 2008). The NGS minerals variation in Chanda-1 and Chanda Deep-1 may likely be attributed to changes in argillaceous influx during the fluvio-deltaic deposition of Datta Formation in this particular depositional basin.

The cross-plots of Chanda-01 And Chanda Deep-01 wells indicate the presence of chlorite along with montmorillonite (swelling clay) and kaolinite (non-swelling clay) (Fig. 6). The occurrence of chlorite likely suggests the supply of abundant Fe- and Mg-rich materials during deltaic depositional setting of sandstone reservoirs. The presence of chlorite is reported to play a role in preserving intergranular porosity and creating better pore–throat structures of sandstones (Aagaard et al. 2000; Chen et al. 2011).

Spontaneous potential (SP) log

The magnitude of SP deflection is the result of the difference in resistivity between mud filtrate (Rmf) and formation water (Rw) (Assaad et al. 2004). If the salinities of the mud filtrate and formation water are similar, there is no SP potential or current flow, and no deflection in SP is observed (Schlumberger 1989). This is the case in the Chanda-1 well. The SP log in the Chanda Deep-1 well at a depth of 4660–4672 m shows deflection to the right. In the Chanda Deep-1 well, SP deflection is generally towards the right, indicating an Rmf < Rw condition (Figs. 3, 4).

Resistivity logs

Maher (1964) provided a complete interpretation of electric logs. According to Maher (1964), sandstone with oil and gas is indicated by the separation of the microresistivity curves, the large deflection of all resistivity curves to the right and the large deflection of the self-potential curve to the left. In Chanda-1, sandstone containing oil or gas and salt water is indicated by the separation of the microresistivity curves (Fig. 3), the large deflection of the short (SN or LLS) and long normal (LN or LLD) curves at the top, and their gradual recession toward the bottom of the left deflection of the lateral curve in the lower part of the log. In the Chanda Deep-1, sandstone-containing salt water is indicated by the separation of the microresistivity curves (Fig. 4), the moderate deflection of the short normal curve to the right, the slight deflection of the log normal curve, the left deflection of the lateral curve and the large deflection of the SP curve to the left. In the Chanda-1, the interval between 4751 m, and 4770 m shows a significant separation between LLS and LLD with LLD > LLS > MSFL profile. In the Chanda Deep-1, a slight separation between LLS and LLD occurs at a depth of 4650–4660, and 4788–4809 m.

NPHI-RHOB logs

At 4751–4771 m, RHOB plots left of NPHI in the Chanda-1; this crossover indicates a hydrocarbon zone. RHOB plots right of NPHI at an interval of 4772–4780 m, indicating shaley intervals. In the Chanda Deep-1, the NPHI-RHOB overlay at an interval of 4650–4660 m indicates the presence of clean, wet sands. RHOB plots right of NPHI at 4662–4674, and 4710–4735 m, indicating shaley intervals.

Gassmann fluid substitution

The significance of fluid substitution in seismic rock physics lies in the fact that it provides a tool for identification and quantification of fluid in a reservoir, which is commonly performed using Gassmann’s equation (Gassmann 1951). Generally, Gassmann relations reflect the variations in P-wave and S-wave velocities due to changes in saturation with simple inputs. The initial inputs are density and P-wave velocity logs, while the matrix bulk modulus (Ko), the frame or dry rock bulk modulus (K*), the porosity (φ), and the rock shear modulus (G) are the constant parameters during substitution (Smith et al. 2003).

Pore fluids have the ability to change the rock properties (Vp, Vs, and density), as well as seismic properties. The calculated shear wave velocities for two wells, using the Greenberg and Castagna (1992) relation, are shown in Fig. 7a, b. The Gassmann fluid substitution was performed on the Datta sands at depth intervals of 4750–4804 m (Chanda-1) and 4650–4810 m (Chanda Deep-1) to model the seismic velocity and density at different water saturation levels (Figs. 8, 9). The input data (Vp, Vs, density, SW, and Vclay) for the application of the Gassmann fluid substitution were obtained from the petrophysical analyses of Chanda-1, and Chanda Deep-1 (Figs. 3, 4). Three saturation models (brine, oil, and gas) were calculated for pure sandstones and were used to measure the sensitivity of the saturation of different sandstones. The models’ quality was checked with respect to one another. The results of the saturation models are listed in Table 2.

Fig. 7
figure 7

a, b Shear velocity QC cross-plots for two wells showing the relationship of Vp and Vs calculated using the Greenberg and Castagna (1992) relationship

Full size image
Fig. 8
figure 8

Elastic impedance logs for Chanda-1 well, showing the calculated parameters (Vp, Vs, AI, Poisson ratio) at different saturation levels (100% water saturation and oil) in reservoir interval

Full size image
Fig. 9
figure 9

Elastic impedance logs for Chanda Deep-1 well, showing the calculated parameters (Vp, Vs, AI, Poisson ratio) at different saturation levels (100% water saturation and oil) reservoir interval

Full size image
Table 2 Gassmann fluid substitution results
Full size table

The fluid substitution cross-plots (Fig. 10a, b) enable to visualize the relationship among the velocities, density, acoustic impedance (AI) and Poisson’s ratio results. The DT curve was calculated using the Greenberg and Castagna (1992) empirical relationships for different minerals. Velocity–density cross-plots, being good discriminators for mechanical to chemical compaction zones, have been plotted in Fig. 11a, b for two wells. The plots show that single clusters can be seen based on the Vp-density cross-plots representing the compaction trend.

Fig. 10
figure 10

a, b Fluid substitution cross-plots of Chanda-1 and Chanda Deep-1, for two wells, showing change (increase) in Vp for the reservoir intervals in two wells

Full size image
Fig. 11
figure 11

a, b Vp-bulk density cross-plots for two wells showing different clusters of all the data points where the blue data points represent the data from two wells at reservoir interval

Full size image

The GR log interpretation results in the identification of sand-bearing zones, based on the boxcar/coarsening upward trend of GR at the Datta sands level. Moreover, on the basis of petrophysical interpretation of GR, DT, RHOB, and PHA logs, these zones were identified as hydrocarbon-bearing (Figs. 8, 9). The important characteristics of the identified zones, including PHA, DT, VSh, and RHOB have been given in Table 1. The trend of the Datta Formation in the GR log shows a boxcar trend. The GR profile for a tide-dominated environment shows different shapes: block left-boxcar, bell-shaped, funnel shaped, and an irregular trend (Cant 1992). In a wave, and storm-dominated environments, wave ripples are thin parallel laminations with mud drapes, large planer cross-bedding, trough cross-bedding, highly bioturbated (skolithos) sandstone, and hummocky cross-stratification. In storm-dominated environment, it shows left-boxcar with no sharp edges on top and bottom (Cant 1992). A saturation effect with different mineralogical composition depends on porosity. The porosity of 100% clean sandstone is higher than the porosity of quartz-clay, which affects the density. With increasing hydrocarbon saturation, there would be a greater difference in density in these two mineralogical settings.

Gassmann fluid substitution was applied to the well data of Chanda-1 and Chanda Deep-1 for the Datta sands intervals (4750–4804 and 4650–4811 m). The purpose was to generate seismic responses at different saturation levels and compare them with the seismic response at the initial saturation condition of the well. The initial water saturation levels obtained from petrophysical analysis of wells Chanda-1, and Chanda Deep-1 fell in the range of 31–36% within the depth ranges of 4750–4804 and 4650–4811 m, respectively. There was a significant change in Vp when the initial water saturation level was substituted with the hydrocarbon saturation level. The value of density decreased quite significantly in both the wells when the brine saturation level was substituted with oil saturation.

The rock properties are effected significantly due to fluid substitution. A rock’s physical properties (Vp, Vs, and density) change with variations in levels and types of pore fluid saturation (Figs. 9, 10). The average Gassmann results for the two wells are listed in Table 2. The Poisson ratio in both wells was 0.16, as indicated from Figs. 9 and 10 and Table 2. The dry rock properties (bulk modulus, shear modulus, Poisson ratio, and modulus) for the two wells show similar values, indicating no difference in the compaction level of clastic rocks in the area. The Vp in Chanda Deep-1 was more variable. The Vs in Chanda-1 and Chanda Deep-1 remained unaffected (Figs. 9, 10), and showed no sharp contrast. The acoustic impedance log in both wells shows a slight decrease from 100% brine saturation to oil saturation. The change exhibited by Vp and density shows the variation in AI contrast (product of Vp, and density) at the reservoir level. This variation in the AI can be used to generate synthetic seismograms at the reservoir interval for comparison with the newly acquired seismic data of the area under investigation.

Figure 11a, b shows the fluid substitution plots for Chanda-1 and Chanda Deep-1. The Vp curve in Chanda-1 shows a drastic change displaying a steep slope while the curve in Chanda Deep-1 is more gentle. The Vp in Chanda-1 is lower at 60% water saturation (SW), while it increases with the increase in water saturation from 80 to 100%. Likewise, in Chanda Deep-1, the Vp is consistent up to 60% water saturation with a gentle increase at 80%. There is a gradual increase in Vp response from 60% onwards.

Reservoir characterization enables us to describe numerous reservoir properties using the available data set to generate reliable models for precise prediction of reservoir performance. In this study, petrophysics, rock physics cross-plots, and Gassmann fluid substitution analysis were applied to characterize the reservoir in the Chanda oil field, northwest Pakistan. The results of this study have led us to conclude that there is a slight increase in Vp and a decrease in density, indicating hydrocarbon saturation. The petrophysical analysis, combined with fluid substitution, also confirms the type of fluid present within the reservoir. Although the fluid has no influence on Vs, saturation changes caused by fluids lighter than brine may change the Vs due to the density effect. Rock properties can be different for the same rock with brine when compared to saturation. There is a decrease in the density curve as observed in Fig. 11, but the shear wave velocity remained unaffected. The Vp is constant at 100% water saturation, with a slight change due to hydrocarbon saturation. The Vp shows a profound increase at above 60%, as indicated by the cross-plot (Fig. 11a). Both of the rock’s physical properties (Vp, and Vs) increase with the decrease in effective density. When the percentage of hydrocarbon saturation was increased, there was an observed decrease in the density because oil is less denser than water.

The main implication of the present work lies in the fact that subject to the availability of good-quality seismic data, synthetic seismograms may be generated from velocity and density models for different saturation levels. These synthetic seismograms could then be used to determine future optimum well locations once they are compared with the newly acquired data at the reservoir level. Hence, this study is of benefit in the development phase to map the saturation distribution of the reservoir at the desired levels. The elastic properties derived from rock physics are important considerations for the comprehensive understanding and use of the seismic data, as well as for future production and reservoir engineering activities.

Seismic anisotropy defines the directional dependence of the velocity of seismic waves in a rock and is used in petroleum exploration and production. The reservoir quality of clastic rocks has been studied using seismic anisotropy (Kendall et al. 2007). Wang (2002) measured velocity and anisotropy of many shale and reservoir rocks from oil and gas fields around the world and concluded that clays and fine layers in sedimentary rocks are the main causes of seismic anisotropy, whereas little intrinsic anisotropy exists in unfractured reservoir rocks such as sands, sandstones, and carbonates under reservoir conditions. Pore fluids have a large effect on seismic signatures. This study combines Gassmann’s fluid substitution recipe, with petrophysics, to predict velocities in saturated rocks. The results demonstrated in this work are useful to work out the relationship of seismic velocities and fluid saturation in a scenario with inadequate or sparse well dataset. The results could be used by future researchers having a good hold of seismic and additional well dataset to understand the field development assessment of an oil–gas field and interpret ideal well locations in any development field.

Conclusions

Petrophysics typically transforms measurements of GR, resistivity, and porosity into reservoir properties. Rock physics transmutes petrophysical results into Vp and Vs, and RHOB. Fluid substitution based on the Gassmann model is a tool used to map the variation of density at different saturation levels, inferring changes in seismic response. In this study, we presented an integrated analysis of petrophysics and fluid substitution of the Datta sands at the Chanda Oil Field, in northwest Pakistan. Based on the petrophysical interpretation of two wells, reservoir sand packages at the Datta sand level were identified. The crossover formed by density and neutron log, with corresponding sonic values, confirms the hydrocarbon presence in the sand packages. The modeled seismic response (velocities and density) for different saturation levels at the Datta sands predicts a significant increase in Vp as compared to Vs, which remain unaffected, and a decrease in density. This identified variation can be demonstrated using synthetic seismograms, which can be tied to the seismic data to map the saturation level of the subsurface. Such comparisons may be helpful during the development phase of a hydrocarbon field in minimizing the risk of well failure due to increased water saturation in the subsurface. The main conclusions derived from this study are:

  1. 1.

    The log analysis shows that the Datta sands of the Chanda Field reflect excellent reservoir characteristics. On the basis of petrophysical analyses, one hydrocarbon-bearing zone was identified in Chanda-1, while four such zones were identified in Chanda Deep-1. The reservoir interval has an average net sand thickness of 19–176 m and an average porosity of 7–13%, whereas the water saturation (SW) ranges from 31 to 36%.

  2. 2.

    Left boxcar trend and irregular trend are common in the GR log signature of both wells, typical of a braided, fluvial environment.

  3. 3.

    Significant separation exists between the LLS and LLD logs at intervals of 4751–4770 m in Chanda-1, and 4650–4660 and 4788–4809 m in Chanda Deep-1, indicating good permeable reservoir sands.

  4. 4.

    Cross-plots show clean sandstone in Chanda-1, whereas in Chanda Deep-1 shale content is relatively high, indicating a shale-free lithology in the west, and shale-rich lithology in the east of the area. Mineralogically, sandstone appears micaceous in Chanda-1, while arkosic in Chanda Deep-1 well.

  5. 5.

    Gassmann fluid substitution performed at the Datta clastics level indicates a variation in acoustic properties (velocity and density) of the reservoir for different fluid saturation levels (100% water saturation, and oil saturation). Three saturation models (brine, oil, and gas) have been calculated for pure sandstones, and utilized to see the sensitivity of saturation in different sandstones, and have been correlated with respect to each other.

  6. 6.

    Fluid substitution and lithology substitution modeling produce logs that reflect former or future conditions of a project and can be used to envisage log characteristics in various undrilled parts of the field.