Abstract
This study presents an approach to determine the dimensions of three-phase separators. First, we designed different vessel configurations based on the fluid properties of an Iranian gas condensate field. We then used a comprehensive computational fluid dynamic (CFD) method for analyzing the three-phase separation phenomena. For simulation purposes, the combined volume of fluid–discrete particle method (DPM) approach was used. The discrete random walk (DRW) model was used to include the effect of arbitrary particle movement due to variations caused by turbulence. In addition, the comparison of experimental and simulated results was generated using different turbulence models, i.e., standard k–ε, standard k–ω, and Reynolds stress model. The results of numerical calculations in terms of fluid profiles, separation performance and DPM particle behavior were used to choose the optimum vessel configuration. No difference between the dimensions of the optimum vessel and the existing separator was found. Also, simulation data were compared with experimental data pertaining to a similar existing separator. A reasonable agreement between the results of numerical calculation and experimental data was observed. These results showed that the used CFD model is well capable of investigating the performance of a three-phase separator.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
On production units, a multiphase separator is the first surface equipment which is used to separate the produced wellhead fluid into the liquid and gas fractions. Inappropriate design of three-phase separators is a major obstacle to stable hydrocarbon processing and leads to reduce the efficiency of the entire surface equipment such as: heaters, exchangers and pressure maintenance equipment. When sizing a horizontal separator, it is necessary to choose a seam to seam vessel length and a diameter (Stewart and Arnold 2008). In the semiempirical method, the separator length and diameter are chosen, in order to allow different phases to separate from each other and reach an equilibrium. Much work has been conducted to investigate the aspects of designing three-phase separators (GPSA 1998; Smith 1987; Gerunda 1981 and Watkins 1967). Bothamley (2013a, b, c) conducted a complete study for quantifying the separation performance. The effects of different types of momentum breaker and mist extractor device, feed pipe velocity, particle-size distribution and the main vessel dimensions were discussed in their work.
Although useful guidelines are provided by the semiempirical approach, the essential data that affect the separator performance are not always considered (Kharoua et al. 2013). The semiempirical method does not, for example, consider the effects of liquid re-entrainment and recirculation within the liquid layers (Viles 1993; Shaban 1995). In addition, this method uses a single representative particle size for oil and water phases. This is not always the case since previous studies stressed the importance of the secondary-phase distribution in predicting the performance of three-phase separators (Monnery and Svrcek 1994; Kharoua et al. 2013). It should also be emphasized that the semiempirical method could not forecast the separation efficiency since it is based on 100% separation (Stewart and Arnold 2008). These fundamental limitations of a semiempirical method illustrate the need for a more detailed method to investigate the three-phase separation phenomena. CFD simulations will be able to investigate the three-phase separation phenomena and provide some useful guidelines for optimization of dimensions.
There are two methods for dealing with multiphase flow, the Eulerian–Lagrangian approach and the Eulerian–Eulerian approach. The Eulerian–Lagrangian method deals with the continuous fluid phase as a continuum by solving the Navier–Stokes equation, while the secondary-phase particles are tracked in their movements through space and time. The Eulerian–Lagrangian approach is preferred over the Eulerian–Eulerian approach when information about particle locations is needed. The other advantage of the Eulerian–Lagrangian approach is physically concrete modeling of fluid–particle interaction. Nevertheless, the computing time of Eulerian–Lagrangian method significantly increases by increasing the number of tracked particles. Therefore, the main detraction of using the Eulerian–Lagrangian approach is the computational expense (Chrigui 2005; Mpagazehe 2013). Conversely, the Eulerian–Eulerian method mathematically focuses on the fluid motion in a specific location in space. The VOF model, the mixture model and the Eulerian model belong to the Eulerian–Eulerian approach. The VOF model is used when the position of the interface between fluids is important. The mixture model is used to model homogeneous multiphase flows where the phases move at almost same velocities. The Eulerian multiphase model is used to model separate but yet interacting phases. It should be noted that in the Eulerian multiphase model a single pressure is shared by all phases (Mahmud et al. 2018; Zakerian et al. 2018; Fluent Theory Guide 2016; Sun et al. 2014).
Previously, numerical studies of three-phase separators mostly used the Eulerian–Eulerian method. Vilagines and Akhras (2010) used the CFD model to evaluate the effect of new internals on the efficiency of a three-phase separator. They used the shear stress transport turbulence model and three-phase Eulerian model to simulate the multiphase flow. In that study, the results of the CFD simulation and the experimental data were not compared. Kharoua et al. (2012) used a CFD model to modify a production separator. The well-known k–ε turbulence model and the Eulerian–Eulerian multiphase approach were used to study the three-phase separation phenomena. Again, in that study, the numerical calculation results were not compared with the experimental data.
Kharoua et al. (2013) used the CFD model to analyze the performance and internal multiphase flow behavior in a three-phase separator. To deal with complex phenomena such as size distribution, coalescence and breakup of secondary phases, the population balance model (PBM) was used. Three different liquid particle distributions were used to determine the effect of size distribution of the secondary phase on the performance of the separator. The simulation results stressed the importance of the secondary-phase distribution in predicting the performance of the internal flow behavior. However, the PBM model was applied to one liquid phase and the other liquid phase was represented by a mono-dispersed distribution. In that study, the results of numerical calculation were compared with industrial data. A very poor agreement between the outcomes of the CFD simulation and the experimental data was observed. In addition, the details of the sampling procedures and experimental methods were not presented in their study.
There are also a few publications that made use of the Eulerian–Lagrangian method. Laleh et al. (2011) applied numerical calculations to study the fluid flow behavior in two-phase separators. In their paper, two simulation approaches, the DPM model and a combination of VOF and DPM model, were used to simulate the multiphase flow. In addition, the k–ε turbulence model was used because of its simplicity and achieved accuracy. Their simulation results demonstrated that the combination of VOF and DPM models was more reliable than the DPM model with respect to predicted separation efficiency. Laleh et al. (2012a, b, 2013) used DPM, VOF and k–ε turbulence models to develop a realistic CFD simulation in order to debottleneck a three-phase separator. In that study, the flow-distributing baffles and the mist extractor were modeled as porous media. However, the results of the CFD simulation and the experimental data were not compared in their work.
This study presents an approach to determine the dimensions of three-phase separators. First, based on the Arnold and Stewart semiempirical procedure, we developed a computer code to design several configurations with varying slenderness ratios for one of the Iranian south gas condensate reservoirs. We then devised a comprehensive CFD model to investigate the three-phase separation phenomena.
In this study, the commercial CFD code ANSYS Fluent version 16.2 was utilized. For simulation purposes, two multiphase models, VOF and DPM, were combined with the k–ε turbulence model, while the DRW model was implemented to include the effect of arbitrary particle movement due to velocity variations caused by turbulence. The results of numerical calculations in terms of fluid profiles, separation performance and DPM particle behavior were used to choose the optimum vessel configuration. To evaluate the proposed method, the optimized length and diameter of the separator were compared with those of one currently used by National Iranian Oil Company (NIOC). No difference between the dimensions of the optimum vessel and the existing separator was found. Also, simulation data were compared with experimental data pertaining to a similar existing separator. A reasonable agreement between the experimental data and the simulation results was observed.
Before presenting the simulation methodology, it is important to highlight the most important modifications of this study. These modifications are listed as follows:
-
The quality of computational grid systems was not validated in previous studies. In addition, many previous studies used the general mesh qualities such as the maximum aspect ratio to validate the computational grid systems. However, the results of this study will show that the general mesh qualities are not sufficient to investigate the computational mesh. Therefore, the mesh independence test is an important aspect of simulating the three-phase separators.
-
Comparison of numerical simulation results and experimental data is an important aspect of the CFD study. However, most of the CFD studies on three-phase separators did not validate the CFD simulations with the experimental or field test data. This is presumably because of the high cost required for conducting such tests. In the present study, simulation results are compared with industrial data pertaining to a similar existing separator. In addition, this study presents the details of the sampling procedures used to collect fluids and the experimental methods used to evaluate the efficiency of three-phase separators.
-
The effect of arbitrary particle movement due to variations caused by the turbulence was ignored in previous studies. However, the results of this study underline the importance of this factor in predicting the performance of three-phase separators.
-
The present study is meant for establishing a suitable methodology, including turbulence model selection for simulating the three-phase separation phenomena. As a result, the comparison of experimental and simulated results was generated using different turbulence models, i.e., standard k–ε, standard k–ω and RSM.
-
One important parameter that has received inadequate attention thus far in designing separators is the change in input water and gas flow rates. This negligence can eventuate in problems such as rising of the water level in separator, difficulties in operational three-phase separation, increasing volumetric water fraction in natural condensate and gas outlets and finally reducing efficiency of separators. In this work, the effect of input gas and water flow rates on the three-phase separation performance is investigated.
-
Previous studies have defined different ranges of slenderness. These guidelines for the slenderness ratio are mainly determined by economic analysis without thorough investigation of the three-phase separation phenomena (Laleh et al. 2012a, b). In this study, the effect of the slenderness ratio on the three-phase separation phenomena and behavior of secondary-phase particles are investigated. In addition, the slenderness ratio of the optimum vessel is compared with the slenderness ranges proposed in the literature.
-
Finally, most of the CFD studies on three-phase separators only provided the overall steps of CFD modeling. However, this study presents the details of the used CFD model.
Implemented semiempirical approach
In the semiempirical method, the separator length and diameter are chosen, in order to allow the water and condensate droplets to separate from the continuous gas phase and reach an equilibrium. Several semiempirical methods for sizing two- and three-phase separators have been presented before (Arnold and Stewart 1998; Stewart and Arnold 2008; Monnery and Svrcek 1994; Dokianos 2015; Hernandez-Martinez and Martinez Ortiz 2014). Of all the previous methods, the Arnold and Stewart procedure is the most suitable for designing a three-phase separator, due to its robustness and simplicity (Olotu and Osisanya 2013; Ghaffarkhah et al. 2017).
The software developed in our study was based on the Arnold and Stewart procedure for calculating the dimensions of three-phase separators. This software eliminates the risk of mistakes and increases the reliability of the semiempirical procedure. The most important equations of this software are summarized below.
Gas capacity formula
The gas capacity constraints are provided by the following equation (Stewart and Arnold 2008):
where \( \alpha_{\text{l}} \) is the ratio of liquid area to the total area of the separator, \( \beta_{\text{l}} \) is the ratio of liquid height to total height of the separator, \( L_{\text{eff}} \) is the effective length of the vessel in m, \( T \) is the operating temperature in K, \( Q_{\text{g }} \) is the gas flow rate in scm/h, \( P \) is the operation pressure in kPa, \( Z \) is the gas compressibility, \( d_{\text{p}} \) is the liquid droplet diameter in μm, and \( C_{\text{D}} \) is the drag coefficient.
Liquid capacity formula
The liquid capacity constraint, based on retention time, is defined by the following formula (Stewart and Arnold 2008):
Here, \( Q_{\text{w}} \) is the water flow rate in m3/s, \( t_{\text{rw}} \) is the water retention time in min, \( Q_{\text{o}} \) is the oil flow rate in m3/s, and \( t_{\text{ro}} \) is the oil retention time in min.
Seam to seam length formula
The seam to seam length of the separator is given by the following equations (Stewart and Arnold 2008).
For gas capacity constraint:
For liquid capacity constraint:
Here, \( L_{\text{ss}} \) is the seam to seam length of the separator in m and D is the separator diameter in m.
Eventually, several separator configurations with different slenderness ratios \( \left( {\frac{{L_{\text{ss}} }}{D}} \right) \) were computed by our software. Note that in this study, the design of the vessel is based on the gas capacity constraint. It should also be emphasized that the separator seam to seam dimensions were reported in multiples of 100 mm, while the vessel diameters were in multiples of 50 mm.
The optimum dimensions of three-phase separators are the smallest dimensions that allow different phases effectively separate from each other. Routinely, the optimum dimensions of vessels are estimated based on the guidelines for slenderness ratio. Previous studies have defined different ranges of slenderness (Table 1). These guidelines for the slenderness ratio are mainly determined by economic analysis without thorough investigation of the three-phase separation phenomena (Laleh et al. 2012a, b). As a result, there is a need for a thorough and detailed method to determine the effect of the slenderness ratio on the separation performance and eventually choose the optimum dimensions of horizontal three-phase separators. CFD simulations will be able to examine the efficiency of vessels for different slenderness ratios and provide some useful guidelines for optimization of dimensions. In the present study, the results of numerical calculations in terms of fluid profiles, separation performance and DPM particle behavior are used to choose the optimum vessel configuration. In addition, the slenderness ratio of the optimum vessel is compared with the slenderness ranges proposed in the literature.
Computational methodology
A 3D, transient mathematical model is developed to simulate the three-phase separation phenomena. The VOF model was used to create the background of the computational domain, while the DPM model was used to describe the properties of fluid droplets that were injected at the separator inlet. In addition, the DRW model was used to include the effect of arbitrary particle movement due to variations caused by turbulence. Note that in the DRW model, the interaction of a particle with a series of fluid-phase turbulent eddies is simulated (Fluent Theory Guide 2016; Gosman and Loannides 1983).
Mathematical formulation
The VOF multiphase model belongs to the Eulerian–Eulerian approach. In this model, a single set of momentum equations is solved and the resulting velocity field is shared among the phases. In this study, the gas and liquid phases are treated as incompressible. In addition, the gas phase is defined as the primary phase, while the condensate and water phases are defined as the secondary phases.
The continuity equation (the volume fraction equation) for one of the phases (phase m) is given as follows (Le and Zhou 2008; Irani et al. 2010)
where \( \vec{U}_{\text{m}} \) is the velocity of phase m in m/s, \( \alpha_{\text{m}} \) is the volume fraction of phase m, which has a value in the closed interval from zero to one, and \( S_{\text{m}} \) is the mass source term in kg/s m3. In this study, the mass source term on the right-hand side of Eq. 5 is zero.
The above-mentioned equation is solved for n − 1 phases, whereas the primary-phase volume fraction is determined based on the following equation:
The momentum equation for the VOF model is defined as (De Schepper et al. 2008):
where \( \overrightarrow {U } \) is the average fluid-phase velocity in m/s. It should be noted that when the discrete and continuous phases are coupled, the momentum gained or lost by the particle stream can be incorporated in the subsequent continuous-phase calculations (Fluent Theory Guide 2016; Kishan and Dash 2009). In Eq. 7, \( F_{\text{s}} \) is the momentum transfer term exerted by discrete particles in N/m3.
On the other hand, the DPM model was used to track the secondary-phase particles. In this model, the continuous phase is simulated by solving the Navier–Stokes equations, and the secondary-phase particles are tracked based on integrating the following equation (Shukla et al. 2011):
Here \( u \) is the fluid-phase velocity in m/s, \( u_{\text{p}} \) is the particle velocity in m/s, \( \rho_{\text{p}} \) is the density of particles in kg/m3, and \( \rho \) is the fluid-phase density in kg/m3. \( \vec{F} \) is the additional acceleration due to other forces (force/unit particle mass) in m/s2, which mainly includes the thermophoretic force, Brownian force, Saffman’s lift force and virtual mass force. In order for the Brownian and thermophoretic forces to take effect, the energy equation must be enabled. The Saffman’s lift force is only recommended for submicron particles. Therefore, these three forces were not taken into the consideration in this study. However, the virtual mass force is modeled based on the following equation (Xu et al. 2013):
\( F_{\text{D}} \) is the drag function, which is defined as (Ounis et al. 1991):
where \( d_{\text{p}} \) is the particle diameter in μm, \( \mu \) is the molecular viscosity of the background phase in Pa s, and \( \text{Re} \) is the Reynolds number, which is modeled as:
Here, \( C_{\text{D}} \) is the drag coefficient, which is obtained by:
while \( a_{1} \), \( a_{2} \) and \( a_{3} \) are constants that are defined by Morsi and Alexander (1972) for several ranges of Re.
In the present study, the DPM model with four-way coupling calculation was used to investigate the statistics of particle trajectories. In this model, the momentum transfer from the continuous phase to the discrete phase is calculated through interchange terms such as drag force. In addition, the momentum gained or lost by the particle stream (condensate and water droplets) is incorporated into the subsequent continuous-phase calculations. Coalescence of particles and their breakup are also modeled by using the DPM model with four-way coupling. When the particle trajectory is calculated, a proper model within the spray model theory (Taylor analogy breakup (TAB) model or wave model) is used to compute the droplet breakup based on the particle Weber number. In addition, the outcomes of the collision model are used for modeling droplet coalescence (Laleh et al. 2012a, b).
Three different turbulence models, i.e., standard k–ε, standard k–ω and RSM, were used in this study. The RSM turbulence model has greater potential to give accurate predictions for complex numerical simulations. However, the modeling of the pressure–strain and dissipation rate terms can significantly compromise the accuracy of the RSM turbulence model (Fluent Theory Guide 2016; Bhaskar et al. 2007). The standard k–ω model solves two transport equations to calculate the turbulent kinetic energy, k in m2/s2, and specific dissipation rate \( \omega \) in 1/s (Fluent Theory Guide 2016; Wilcox 1993). On the other hand, k–ε turbulence model solves two transport equations to calculate the turbulent kinetic energy, k in m2/s2, and turbulent dissipation rate, ε in m2/s2, for the multiphase flow (Shukla et al. 2011; Moraveji et al. 2017). These transport equations are:
where \( \beta \) is the production term of turbulence kinetic energy due to velocity gradients in kg/m s3 and \( \mu_{\text{t}} \) is the turbulent viscosity in Pa s which is defined as:
Here, the model constants are equal to:
The dispersion of the secondary-phase particles, due to the velocity fluctuation of the turbulent background phase, is computed by using the DRW model. When the particle tracking model is combined with the DRW model, the fluid-phase velocity, u, in the DPM tracking model is divided into two parts (Zhao et al. 2008):
where \( \overline{u} \) is the mean velocity in \( m/s \) and \( u^{' } \) is the velocity fluctuation of continuous phase in m/s. When the k–ε turbulence model is used along with DRW model, the value of \( u^{\prime} \) is defined by (Zhang and Chen, 2009):
Here, \( G \) is the unit variance normally distributed random number. The value of \( G \) remains constant until eddies reach the end of their life or the particles cross over to eddies. The eddy lifetime (\( t_{\text{e}} \)) is calculated as follows (Raoufi et al. 2008):
Here, \( t_{\text{L}} \) is the particle Lagrangian integral time in s, which is given as:
where S is the time spent in turbulent motion along the particle path in s.
Furthermore, the following equation is used for calculating eddy crossing time of the particles:
where \( r \) is the particle relaxation time in s and \( L_{\text{e}} \) is the eddy length scale in m.
Material definition
The flow rates and physical properties of fluids are taken from one of the Iranian gas condensate fields as shown in Table 2. The surface tensions of condensate/gas, water/gas and condensate/water were set at 0.02054, 0.06475 and 0.04123 N/m, respectively. Heat transfer has been neglected. This is mainly because the working temperature of the vessel is almost constant. Therefore, all material properties were calculated in this temperature and used in CFD simulations. It should be mentioned that the condensate and water phases were considered as Newtonian fluids.
In order to investigate the size distribution of the secondary-phase particles in the fluid domain, the logarithmic Rosin–Rammler (1933) equation was used.
where \( Y_{\left( d \right)} \) is the mass fraction function, \( \varpi \) is the Rosin–Rammler exponent which describes the material uniformity, \( \overline{d} \) is the Rosin–Rammler diameter in μm, and \( d \) the particle diameter in μm.
Hallanger et al. (1996) utilized a secondary water particle distribution with an average diameter of 250 μm and a Rosin–Rammler exponent of 3 for seven different particle classes. Based on the maximum stable droplet size, Laleh et al. (2012a, b, 2013) generated the particle distribution with a Rosin–Rammler exponent of 2.6 and a maximum diameter of about 2270 and 4000 μm for oil and water phases, respectively. Note that the above-mentioned studies were combined with the actual fluid data provided by NIOC, based on the focus beam reflectance measurement (FBRM), to choose the proper particle distribution model. The maximum, minimum and average diameters for the water phase were set at 2000, 150 and 500 μm. For condensate phase, the maximum, minimum and average diameters of 560, 140 and 50 μm were selected. The Rosin–Rammler exponent, \( \varpi \), at 2.6 was used for both the condensate and water phases.
In the present study, the diameter ranges of the condensate and water droplets are divided into 35 subintervals. Each of these discrete intervals is represented by a mean diameter for which trajectory calculations are performed (Zhang 2009). It should be mentioned that Eq. 21 is used to calculate the mass fraction of each of these subintervals based on its mean diameter. Eventually, the number of injected particles for each of these subintervals is calculated.
Computational domain
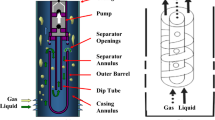
As mentioned in the introduction, a computer program was developed to design different vessel configurations by using the Arnold and Stewart procedure. In order to investigate the three-phase separation phenomena, five different configurations with varying slenderness ratios were chosen among the designed separators. The vessel dimensions and location of internals for each case are presented in Table 3. In the upper part of each vessel next to the protruding inlet nozzle, a spherical inlet diverter was used to rapidly break the momentum and change the direction of fluids. Moreover, the height and location of the weir were accurately calculated to improve the condensate–water separation (Stewart and Arnold 2008; API spec 12J). The overall arrangement of these vessels is shown in Fig. 1a.
As can be seen in Table 3, Cases 3, 6 and 7 have the same seam to seam length and diameter. However, these vessels are equipped with different internals. A spherical inlet diverter is used for Case 3, while Case 6 is equipped with a vane-type inlet diverter. In addition, Case 7 is equipped with a vane-type inlet diverter, perforated plates and a high-efficiency mist extractor device. The comparison between these cases could highlight the effect of different internals on the three-phase separation performance. It should also be emphasized that Case 7 has the dimensions and internals quite similar to those of an industrial separator currently in use for one of the Iranian oil fields. The results obtained from this vessel were reviewed in a CFD evaluation. The overall arrangement of this separator (Case 7) is shown in Fig. 1b. Note that the mist extractor device and perforated plates were modeled as the porous zone, while the curved plates were used for modeling of the vane-type inlet diverter.
Porous zones are modeled by adding a momentum source term to the right-hand side of the VOF momentum equation (Eq. 7). When a cell zone is defined as the porous zone, this momentum source term is determined based on the following equation:
where \( \left| {\vec{U}} \right| \) is the velocity magnitude in m/s, \( 1/\alpha \) is the viscous resistance coefficient in m−2, and \( C_{\text{F}} \) is the inertial resistance coefficient in m−1 (Wang et al. 2014).
The original mist extractor is a type E wire mesh demister. In this study, based on Helsør and Svendsen (2007) work, the porosity, viscosity resistance coefficient and the inertial resistance coefficient of the mist extractor were set at 97.7%, 3.84e6 m−2 and 126 m−1, respectively. Moreover, the flow distribution baffle was modeled as a perforated plate with a free area of 40% and an inertial resistance factor of 1822.1 m−1. Note that the properties of internals were taken from the configuration of the existing NIOC separator for validation purposes.
Boundary conditions
General descriptions of boundary conditions are shown in Table 4. A velocity inlet boundary type and volume fraction of the secondary phases were defined for the fluid inlet, while a pressure outlet boundary type and pure gas condition were used for the gas outlet (Laleh et al. 2012a, b, 2013). In addition, a velocity outlet boundary condition and volume fraction as a pure secondary phase were used for the condensate and water outlets. It should be noted that the velocity at the condensate and water outlets were chosen to maintain the gas–condensate and condensate–water interfaces and to ensure an overall phase mass balance. For the DPM model, the inlet and outlet boundaries were set as an escape zone, while the walls of condensate and water zones were assumed a trap area. Using the particle tracking process, the droplets reaching the separator’s walls (other than the walls of condensate and water zones) reflected and lost their momentum.
Mesh generation and grid independency
The mesh was generated by a tetrahedral/hybrid scheme. Each vessel was divided into different zones, to obtain a more uniform mesh and reduce the total number of computational cells. The generated meshes for Cases 3 and 7 are presented in Fig. 2. This study included for a mesh independence test by increasing the grid count until the same results were obtained for each vessel (Moraveji and Hejazian 2014). Different variables such as the mass distribution of the secondary-phase particles in the fluid domain, velocity, pressure, density and turbulent kinetic energy were compared to find the optimum number of grids. As an example, the results of the grid independency test in terms of the mass distribution of condensate and water droplets in the gas-rich zone of Case 3 are shown in Fig. 3. A grid system with a total number of 1,392,721 cells was used for this case. For a better understanding of mesh modality, the total number of cells, the skew factor and the maximum aspect ratio and squish factor were investigated for each case to determine the overall mesh quality. As an example, the above-mentioned parameters for the different meshing systems of Case 3 are shown in Table 5. Nearly the same overall quality was computed for different meshing systems. However, there is a difference between the grid systems as mentioned before. This showed that calculating the overall mesh quality is not sufficient to investigate the computational mesh. Therefore, the mesh independence test is an important aspect of the CFD study.
Discretization and numerical solution
In this study, the multiphase partial differential equations were discretized using the finite volume method, while the SIMPLE algorithm was used as the pressure–velocity coupling scheme (Patankar and Spalding 1972). Moreover, the first-order upwind approximation was chosen for the discretization of the turbulent kinetic energy, turbulent dissipation rate and momentum equations, while the PRESTO discretization scheme was employed to interpolate the pressure values at the faces of computational cells (Patankar 1980; Peyret 1996). The Geo-Reconstruct interpolation scheme was used for the discretization of the volume fraction. It should be noted that the Geo-Reconstruct interpolation scheme is used whenever the time-accurate transient behavior of the interface between phases is important (Fluent Theory Guide 2016).
Three different time step sizes, i.e., 0.005, 0.001 and 0.0005 s, were tested. The time step 0.005 s is proven to be too large for all cases since it caused several simulation instabilities. Comparison between the other two time steps showed little difference. As a result, the time step size at 0.001 s was used for both the DPM and VOF models. It should be noted that the time step 0.001 s fulfills the Courant–Friedrichs–Lewy (CFL) criterion (CFL < 1). As a result, this time step size does not affect convergence negatively (Fluent Theory Guide 2016). Since the dimensions and the total number of cells were different for Cases 1 to 7, the PC run time was also different for them. For Case 7, a PC run time of 47 h was required to simulate the continuous and discrete phases on two 4.2 GHz CPUs running the 64-bit version of ANSYS Fluent. It should be emphasized that solving multiphase problems is a time-consuming process, which can be hindered by many factors such as the large number of grids and complex computational domains. For this reason, the proper under-relaxation factors for pressure, density, body forces, momentum, turbulent group and discrete-phase sources were accurately chosen at 0.3, 0.9, 1, 0.005, 0.8 and 0.5, respectively, to improve the stability of the solutions. Finally, in this study, the convergence criteria for different equations were set to 10e−4.
Experimental
Fluid sampling
Sampling of the production separator fluids was done with 700-ml liquid sample bottles and 20,000-ml high-pressure gas sample cylinders (Fig. 4). The samplers were connected to the sample source valves on the separator from which the desired sample could be collected. When the cylinders were filled, the sealing valves were set and the samplers were prepared for transfer. In this study, the above-mentioned sampling steps were performed in accordance with ASTM D4177, to avoid sampling errors.
Apparatus setup and measurement method
Determining the amount of water in condensate and gas outlets
The Coulometric Karl Fischer titration method is widely used for moisture analysis in the petroleum industry (Margolis and Hagwood 2003; Ivanova and Aneva 2006 and Kestens et al. 2008). In this method, water reacts with iodine molecules in the presence of sulfur dioxide. The current required to electrolytically generate iodine at the anode is measured and stoichiometrically related to the amount of moisture introduced (Mabrouk and Castriotta 2001). To determine the amount of water in the gas and condensate outlets, the Coulometric Karl Fischer instrument (model AT-710B of KEM, Japan) was used (Fig. 5).
In the present study, the gas sample was directed through the Coulometric Karl Fischer vessel to determine the amount of water in the gas outlet. As can be seen from Fig. 5a, a flow meter and a control valve were placed between the titration cell and the high-pressure gas cylinder to control the flow rate of the injected gas. The gas flow rate was kept at a constant value of 50 ml/min for 3 min. The control valve was then closed and titration continued until all amounts of water consumed.
On the other hand, to determine the amount of water in the condensate outlet, the water evaporator accessory was installed upstream of the titration vessel. In accordance with ASTM D6304, 5 g of the condensate sample was accurately weighed and added to a volumetric flask. The volume was then made up to 10 ml with dry hexane. After this, 1 ml of the dissolved sample was injected into an oven (APD-513 of KEM, Japan). The vaporized sample was then transferred into the titration cell by using dry nitrogen gas with a flow rate of 300 ml/min. Eventually, the titration process continued until all amounts of water consumed. It should be noted that only a small amount of water in the injected nitrogen gas will cause an enormous error in the results. As a result, a high-efficiency gas drying system (Fig. 5b) was used to eliminate the moisture of the injected nitrogen gas.
Determining the amount of condensate in water outlet
The amount of hydrocarbons in the produced water in the surface facilities is routinely determined by gas chromatography with flame ionization detection (GC-FID). The main goal of that method is to identify the total amount of hydrocarbons (ISO 9377-2). Experiments were performed on a Varian CP3800 GC system equipped with FID and DB-1 column (25 m long * 0.32 mm ID *0.25 μm film). The schematic of the GC-FID instrument is shown in Fig. 6. In this study, a particular program was used to control the vaporizing oven (40 °C (0.5 min)–340 °C (0.5 min) @ 15 °C/min).
In this method, an oily water sample is acidified and extracted with hexane. The extracted sample is then purified by passing over a drying agent and injected into the FID injection port of chromatograph. Eventually, different groups of hydrocarbons will leave the column and be detected by the FID section (Yang 2011). For further investigation, the results are continuously transferred to a desktop computer.
Result and discussion
Data validation and experimental outputs
As mentioned before, Case 7 has the dimensions and internals quite similar to those of an industrial separator currently in use for one of the Iranian oil fields. Note that the properties of internals were taken from the configuration of existing NIOC separator. In this section, the results of the used CFD model are compared with the experimental data.
Experimental results
As discussed before, the Coulometric Karl Fischer titration method was used to determine the amount of water in the condensate outlet. The titration curve of condensate is shown in Fig. 7. The titration process continued until all amounts of water consumed. The microgram of consumed water was then determined. Based on this, the volume percentage of water at the condensate outlet was determined (equal to 1994 ppm). It should be mentioned that the total moisture detected curve determines the cumulative titration volume, while the moisture detected within the last plotting interval shows the titration curve when 100 percent of water is titrated.
The amount of water in the gas outlet was determined also with the Coulometric Karl Fischer method. The titration diagram of gas is shown in Fig. 8. In this experiment, the gas sample was directed through the titration cell for 3 min and the titration process continued until all amounts of water consumed. Note that the flow rate of the injected gas was measured by using a gas flow meter. Based on the total volume of the injected gas and the microgram of consumed water, the volume percentage of water at the gas outlet was determined (equal to 51 ppm).
The GC-FID system was used to determine the amount of condensate in the water outlet. In this method, the determination of different types of hydrocarbons gives a preliminary qualitative identification, while the recorded peak heights or areas are used for quantitative analysis. In this experiment, an oily water sample was taken from the water outlet of the existing NIOC separator. The chromatograph response for this sample is shown in Fig. 9. On the x-axis, the time is recorded, whereas the y-axis shows the chromatograph response (Micro DPID response). The amount of hydrocarbons in the produced water was then determined by integrating peak areas of the chromatograph response. The results of this investigation showed that the volume percentage of hydrocarbon at the water outlet was equal to 1980 ppm.
Comparison between CFD results and experimental data
The results of the CFD simulation and the experimental data are compared in Table 6. As can be seen, the standard k–ω could not effectively predict the three-phase separation performance. In addition, although the RSM turbulence model could effectively predict the amount of water in the gas outlet, it is not at all appropriate in predicting the amount of water in the condensate outlet and the amount of condensate in the water outlet. In addition, the computing time of the RSM turbulence model is much higher than the k–ε turbulence model (Zhang et al. 2007). As a result, among the above-mentioned turbulence model, the simulation results, adopting k–ε model is found to have better predictions with experimental results. Note that the results of the CFD simulation with k–ε turbulence and DRW models are more accurate than the results obtained by the CFD simulation with k–ε turbulence model and without DRW model. Based on this, it can be concluded that the combination of VOF, DPM, DRW and k–ε turbulence models can be efficiently used to determine the separation performance of three-phase gas condensate separators. Table 6 also shows that without the use of the DRW model the efficiency of separators is overestimated as the calculated amounts of water and condensate in the separator outlets were too low. It should be emphasized that in the following sections all of the simulations are performed using the combination of VOF, DPM, DRW and k–ε turbulence models.
Choosing the optimum vessel configuration
To choose the optimum vessel configuration, the results of numerical calculations in terms of separation performance, secondary-phase particle behavior and fluid profiles are presented in this section.
Separation performance
The particle tracking procedures along with the DRW model were used to determine the mass distribution of liquid droplets among gas, condensate and water outlets. Figure 10 shows the simulated mass distribution of water and condensate droplets at the gas outlet. Note that in this study the secondary-phase mass percentage is defined as the ratio between the mass of the secondary-phase particles in each location and the total mass of injected particles. As can be seen, the amount of condensate and water droplets at the gas outlet increases by increasing the slenderness ratio of the vessel. Therefore, the gas–liquid separation efficiency reduces by increasing the slenderness ratio.
The simulated mass distribution of condensate and water droplets at the condensate and water outlets is shown in Fig. 11. Again, by increasing the slenderness ratio more water droplets are being carried into the condensate outlet. In addition, the mass percentage of condensate at the water outlet increases by increasing the slenderness ratio. As a result, it can be concluded that the condensate–water separation performance reduces by increasing the slenderness ratio.
For a closer look at the separation performance of each vessel, the diameter distribution of the secondary-phase droplets at the gas outlet was calculated. Note that while these particles move through the computational domain, all of their variables such as their diameter and mass were recorded. As presented in Fig. 12, the mean diameter of the liquid (condensate and water) droplets increases by increasing the slenderness ratio of each vessel. The results also showed that the liquid droplets which exited from the gas outlet of all cases had a minimum diameter greater than 10 microns. It should be noted that mist extractor pads can efficiently remove the droplets greater than 10 microns in diameter (Smith 1987; Laleh et al. 2011). As a result, the gas–liquid separation performance of these vessels might increase tremendously by using a suitable mist extractor.
Secondary-phase particle behavior
Multiple planes were modeled inside the gas zone of each vessel to investigate the microscopic features of the secondary-phase particle behavior (Fig. 13). Then, the condensate and water droplets mass distributions within each plane were calculated. The results of this investigation for the condensate and water phases are shown in Fig. 14. For Cases 4 and 5, the condensate droplets mass percentage increased from a specific point in the vessel. So, we can reach the conclusion that these vessels suffer from carryover phenomena which tremendously reduces the separation performance. This phenomenon indicated condensate carryover inside these vessels is caused by poor condensate–gas separation.
Figure 15a shows the simulated mass distribution of the condensate droplets in the water zone. In addition, the simulated mass distribution of the water droplets in the condensate zone is shown in Fig. 15b. As can be seen, by increasing the slenderness ratio the amount of condensate in the water zone increases. Similarly, the mass percentage of water droplets in the condensate zone increases by increasing the slenderness ratio. As a result, the condensate–water separation performance reduces by increasing the slenderness ratio.
Fluid flow profiles
The velocity vectors for Cases 3 and 5 are shown in Fig. 16. To evaluate the difference between the velocity profiles of these two cases, several vertical planes were put in the middle of these vessels and the average velocity magnitude was then calculated within each of these planes. Figure 17 shows the results of this evaluation for Cases 3 and 5. The simulation results showed that the fluid velocity inside the Case 5 is higher than Case 3. This is mainly because Case 3 has a higher total surface area compared to Case 5. Reducing the velocity of gas phase permits the liquid droplets to coalesce faster and settle out by the action of gravity (Newton 1976). As a result, the separation efficiency of Case 3 is higher than Case 5. Moreover, a small vortex was detected above the condensate outlet in all cases. A vortex could suck some gas out of the vapor space and re-entrain it in the liquid outlets (Stewart and Arnold 2008; Ludwig 1997; Kister 1990). These phenomena will reduce the separation performance and produce tons of problems for downstream equipment. This can be overcome by using a vortex breaker at the condensate outlet.
The numerical calculation results in terms of fluid density are displayed in Table 7. As can be seen, the gas density increases by increasing the slenderness ratio due to more droplets being carried out into the gas outlet. Comparing the gas density of Cases 4 and 5 with the other cases shows that more liquid droplets exited through the gas outlet of these two cases.
In this study, an inefficient condensate–water separation was predicted for Cases 4 and 5 with a higher condensate density in the condensate outlet and a lower water density in the water outlet. As can be seen from Table 7, the fluid density at the condensate outlet of Cases 4 and 5 is higher than other cases. This is mainly because more water droplets are being carried out into the gas outlet of these two cases.
Effect of gas and water flow rates on separator’s efficiency
One important parameter that has received inadequate attention thus far in designing separators is the change in input water and gas flow rates. This change can range from small to large values. This negligence can eventuate in problems such as rising of the water level in separator, difficulties in operational three-phase separation, increasing volumetric water fraction in natural condensate and gas outlets and finally reducing efficiency of separators. Hence, these changes must be brought into account when performing an optimal design for separators. Regarding field observations, the production history of adjacent wells as well as information gathered from the NIOC, the mass flow rate range of 105,608–129,078 kg/h was used for the gas phase, while the mass flow rate range of 9450–18,900 kg/h was used for the water phase.
Figure 18a shows the effect of changing the input gas flow rate on separation of natural condensate from the continuous gas phase. As depicted, reducing the mass flow rate of gas has no significant effects on the amount of natural condensate in the gas outlet of all cases. On the other hand, increasing the gas flow rate dramatically raises the amount of natural condensate in the gas outlet of Cases 4 and 5. In other words, the growth in gas flow rate restricts the ability of Cases 4 and 5 in separating natural condensate from the gas phase. Figure 18b demonstrates the influence of changing the gas flow rate on separation of water from the continuous gas phase. These data clearly show that reducing gas rate has no significant effects on the amount of water in the gas outlet of all cases. Conversely, increasing the gas flow rate eventuates in a larger amount of water droplets in gas outlet of Cases 4 and 5. This again shows that the separation performance of Cases 4 and 5 reduces by increasing the gas flow rate.
Figure 19a shows the effect of raising the water flow rate on its mass percentage in the natural condensate outlet. As it is clear, increasing the mass flow rate of water has no significant effects on the amount of water in the natural condensate outlet of all cases. As a result, increasing the water flow rate in the above-mentioned range could not affect the liquid–liquid separation performance of Cases 1–5. Figure 19b shows the effect of increasing the water flow rate on its mass percentage in the gas outlet. Increasing the water flow rate dramatically raises the amount of water in the gas outlet of Cases 4 and 5. This again shows that Cases 4 and 5 could not effectively handle increasing the input flow rates.
Considering the above-mentioned results in conjunction with the total cost of the separator, it was decided to opt for Case 3 as the best configuration. It should be mentioned that the smaller the diameter, the less the vessel will weigh and therefore the lower it cost (Stewart and Arnold 2008; Mulyandasari 2011). A high condensate–water separation performance along with a low water content at the condensate outlet was predicted for this case. In addition, the high condensate percentage at the gas outlet in this case could have been decreased by using a suitable mist extractor. It should also emphasize that vessel number three can effectively handle increasing the gas and water flow rates. The dimensions of this vessel were compared with the length and diameter of the existing three-phase separator of NIOC, which was a three-phase horizontal separator with a seam to seam length of 5000 mm and a diameter of 1850 mm. No difference in dimensions of the Case 3 and existing vessel was observed.
As mentioned before, previous studies have defined different ranges of slenderness. Figure 20 compares the slenderness ratio of Cases 1–5 and the slenderness ranges proposed in the literature. As can be seen, the slenderness ratio of the optimum vessel was just in the range proposed by Smith (1987).
In addition, even the range proposed by Smith (1987) could not guarantee designing the optimum vessel configuration. This is mainly because choosing different slenderness ratios in this range resulted in different vessel dimensions. As can be seen from Fig. 20, the slenderness ratios of Cases 2–5 are in the range proposed by Smith (1987). The semiempirical model could not investigate the efficiency of these vessels and choose the optimum configuration. However, as mentioned before, the used CFD model is well capable of investigating the three-phase separation phenomena and choosing the optimum vessel configuration. This again shows the benefits of the used CFD model in designing three-phase separators.
Effect of different internals on the separation performance
In order to understand the effect of different internals on the separation performance, multiple planes were modeled inside the gas zone of Cases 3, 6 and 7. Then, the condensate and water droplets mass distributions within each plane were calculated. Figure 21 shows the results of this investigation. Comparing the results of Cases 6 and 7 (with vane-type inlet diverter) and Case 3 (with semi-spherical inlet diverter) showed that the mass distribution of the condensate and water droplets near the gas outlet of Cases 6 and 7 was less than Case 3. As a result, less liquid droplets are being carried into the gas outlet of these two cases. Using the vane-type inlet diverter, the liquid droplets reaching the curved vanes lost a considerable amount of their momentum. Therefore, the amount of water and condensate droplets was significantly higher near the vane-type inlet diverter zone, while the mass distribution of the condensate and water droplets was lower in the other parts of Cases 6 and 7. These results readily showed that the efficiency of the vane-type inlet diverter is higher than the semi-spherical momentum breaker.
As we mentioned before, a perforated plate and a mist extractor were modeled inside the gas zone of Case 7 (ref. Figure 1a). In the mist extractor, liquid droplets coalesce and fall to the liquid zone (Stewart and Arnold 2008). In addition, perforated plates are used to improve the flow distribution, increase the liquid residence time and enhance the separation (Lu et al. 2007; Laleh et al. 2012a, b). As a result, the mass distribution of the condensate and water droplets slightly reduced after passing through the above-mentioned internals of Case 7.
In order to investigate the effect of different internals on the liquid–liquid separation performance, the mass distribution of condensate and water droplets in the condensate and water zones was calculated. The results of this investigation are shown in Fig. 22. As can be seen, the mass distribution of the condensate droplets near the water outlet of Cases 6 and 7 was less than Case 3. Similarly, the mass percentage of water droplets in the condensate zone of these two cases was less than Case 3. As a result, it can be concluded that the condensate–water separation performance of Cases 6 and 7 was higher than Case 3.
Comparing the results of Cases 6 and 7 showed that the mass distribution of the condensate droplets near the water outlet of Case 7 was less than Case 6. Similarly, the amount of water near the condensate outlet of Case 7 was less than Case 6. This is mainly because the liquid residence time was increased due to installation of the perforated plates. It should be noted that increasing the condensate residence time indicates that the water phase provides more time for condensate droplets to rise up and join the condensate phase. In addition, increasing the water residence time indicates that the condensate phase provides more time for the water droplets to settle down and join the water phase.
As mentioned before, the coalescence and breakup of particles were considered in the present study. The simulation results showed that the droplet coalescence happened at a very low rate of less than 0.5% in Cases 3, 6 and 7. However, the droplet breakup was more common. For Cases 3, 6 and 7, the droplet breakup occurred at a significant rate of 15.10, 17.94 and 18.37%, respectively. As a result, it can be concluded that the installation of the vane-type momentum breaker and perforated plates increased the number of breakups.
Conclusion
This study presented a comprehensive CFD model to determine the optimum dimensions of three-phase separators. Using the fluid properties of an Iranian gas condensate field, several vessel configurations were designed. Then, the results of numerical calculations in terms of fluid profiles, separation performance and DPM particle behavior were used to choose the optimum vessel configuration. The summary of the results acquired by this model is mentioned below:
-
1.
The general mesh qualities are not sufficient to investigate the computational mesh. Therefore, the mesh independence test is an important aspect of simulating the three-phase separators.
-
2.
The results underlined the importance of the DRW model and showed that without applying this model the computational setup tends to overestimate the separation efficiency.
-
3.
The results showed that the three-phase separation performance reduces by increasing the slenderness ratio.
-
4.
The optimum vessel configuration can effectively handle increasing the gas and water flow rates.
-
5.
No difference between the dimensions of the optimum vessel and the existing separator was found.
-
6.
The slenderness ratio of the optimum vessel was compared with the slenderness ranges proposed in the literature. The results showed that the slenderness ratio of the optimum vessel was just in the range proposed by Smith (1987).
-
7.
Among the used turbulence models, the simulation results, adopting k–ε model is found to have better predictions with experimental results.
-
8.
The results of numerical calculation were compared with industrial data. A reasonable agreement between the outcomes of the CFD simulation with DRW model and the experimental data was observed.
-
9.
The efficiency of the optimum vessel configuration (Case 3) was improved due to installation of a vane-type inlet diverter, perforated plates and a high-performance mist extractor.
Abbreviations
- \( C_{\text{D}} \) :
-
Drag coefficient
- \( C_{\text{F}} \) :
-
Inertial resistance coefficient, \( L^{ - 1} \) (\( {\text{m}}^{ - 1} \))
- \( C_{1 } , C_{2} ,C_{M} \) :
-
Constants in turbulent transport equations
- \( d_{\text{p}} \) :
-
Liquid droplet diameter, \( L \) (μm)
- \( \overline{d} \) :
-
Rosin–Rammler diameter, \( L \) (μm)
- \( D \) :
-
Separator diameter, L (m)
- \( F_{\text{D}} \) :
-
Drag function
- \( F_{\text{s}} \) :
-
Momentum transfer term exerted by discrete particles, \( {\raise0.7ex\hbox{${ m}$} \!\mathord{\left/ {\vphantom {{ m} {t^{2} L^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t^{2} L^{2} }$}} \) (N/m3)
- \( G \) :
-
Unit variance normally a distributed random number
- \( g \) :
-
Gravity acceleration, \( {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L {t^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t^{2} }$}} \) (m/s2)
- \( L_{\text{e}} \) :
-
Eddy length scale, \( L \) (m)
- \( L_{\text{eff}} \) :
-
Effective length of the vessel, L (m)
- \( L_{\text{ss}} \) :
-
Seam to seam length of the vessel, L (m)
- \( \left( {\frac{{L_{\text{ss}} }}{D}} \right) \) :
-
Slenderness ratio
- \( P \) :
-
Vessel operation pressure, m/Lt2 (\( {\text{kPa}} \))
- \( Q_{\text{o}} \) :
-
Oil flow rate, L3/t (m3/s)
- \( Q_{\text{g}} \) :
-
Gas flow rate, L3/t (scm/h)
- \( Q_{\text{w}} \) :
-
Water flow rate, L3/t (m3/s)
- \( S_{\text{m}} \) :
-
Mass source term, \( {\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m {t \cdot L^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t \cdot L^{3} }$}} \) (kg/s m3)
- \( r \) :
-
Particle relaxation time,\( t \) (s)
- \( t_{\text{cross}} \) :
-
Eddy crossing time of the particles, \( t \) (s)
- \( t_{\text{ro}} \) :
-
Theoretical residence time of oil, \( t \) (min)
- \( t_{\text{rw}} \) :
-
Theoretical residence time of water, \( t \) (min)
- \( T \) :
-
Operating temperature, \( \theta \) (K)
- \( t_{\text{e}} \) :
-
Eddy lifetime, \( t \) (s)
- \( t_{\text{L}} \) :
-
Particle Lagrangian integral time, \( t \) (s)
- \( \vec{U} \) :
-
Average fluid-phase velocity, L/t (m/s)
- \( u \) :
-
Fluid-phase velocity, L/t (m/s)
- \( u_{\text{p}} \) :
-
Particle velocity, L/t (m/s)
- \( u^{\prime} \) :
-
Velocity fluctuation of the continuous phase, L/t (m/s)
- \( \vec{U}_{\text{m}} \) :
-
Velocity of phase m, L/t (m/s)
- \( \left| {\vec{U}} \right| \) :
-
Velocity magnitude, L/t (m/s)
- \( Z \) :
-
Gas compressibility factor
- \( \alpha_{\text{l}} \) :
-
Ratio of liquid area to total area of the separator
- \( \alpha_{\text{m}} \) :
-
Volume fraction of phase m
- \( {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}} \) :
-
Viscous resistance coefficient, \( L^{ - 2} \) (\( {\text{m}}^{ - 2} \))
- \( \beta \) :
-
Production term of turbulence kinetic energy due to velocity gradients, m/L⋅(kg/m s3)
- \( \beta_{\text{l}} \) :
-
Ratio of liquid height to total height of the separator
- \( \varepsilon \) :
-
Turbulent dissipation rate, L2/t3 (m2/s3)
- \( k \) :
-
Turbulent kinetic energy, L2/t2 (m2/s2)
- \( \mu \) :
-
Molecular viscosity, m/Lt (Pa s)
- \( \mu_{\text{t}} \) :
-
Turbulent viscosity, m/Lt (Pa s)
- \( \rho \) :
-
Density, m/L3 (kg/m3)
- \( \rho_{\text{g}} \) :
-
Gas density, m/L3 (kg/m3)
- \( \rho_{\text{l}} \) :
-
Liquid density, m/L3 (kg/m3)
- \( \rho_{m} \) :
-
Density of phase m, m/L3 (kg/m3)
- \( \sigma_{k} ,\sigma_{\varepsilon } \) :
-
Constants in turbulent transport equations
- \( \varpi \) :
-
Rosin–Rammler exponent
- CFD:
-
Computational fluid dynamic
- DPM:
-
Discrete particle method
- DRW:
-
Discrete random walk
- FBRM:
-
Focus beam reflectance measurement
- NIOC:
-
National Iranian Oil Company
- PBM:
-
Population balance model
- RSM:
-
Reynolds stress model
- VOF:
-
Volume of fluid
References
Abdel-Aal HK, Aggour MA, Fahim MA (2015) Petroleum and gas field processing. CRC Press, Boca Raton
Abdi M (2002) Design and operations of natural gas handling facilities. Course prepared for the training department of National Iranian Gas Company, Tehran
ANSYS Fluent version 16.2: Fluent Theory Guide (2016). ANSYS help viewer
API Specification 12J (2008) Specification for oil and gas separators, 8th Edition
Arnold K, Stewart M (1998) Design of oil-handling systems and facilities. Gulf Professional Publishing, Texas
ASTM D4177 (1995; R 2010) Standard practice for automatic sampling of petroleum and petroleum products
ASTM D6304 (2007) Standard test method for determination of water in petroleum products, lubricating oils, and additives by coulometric Karl Fischer titration
Bhaskar KU, Murthy YR, Raju MR, Tiwari S, Srivastava JK, Ramakrishnan N (2007) CFD simulation and experimental validation studies on hydrocyclone. Min Eng 20(1):60–71. https://doi.org/10.1016/j.mineng.2006.04.012
Bothamley M (2013a) Gas/liquid separators: quantifying separation performance-part 1. Oil Gas Facil 2(04):21–29. https://doi.org/10.2118/0813-0021-OGF
Bothamley M (2013b) Gas/liquids separators: quantifying separation performance-part 2. Oil Gas Facil 2(05):35–47. https://doi.org/10.2118/1013-0035-OGF
Bothamley M (2013c) Gas/liquids separators: quantifying separation performance-part 3. Oil Gas Facil 2(06):34–47. https://doi.org/10.2118/1213-0034-OGF
Chrigui M (2005) Eulerian–Lagrangian approach for modeling and simulations of turbulent reactive multi-phase flows under gas turbine combustor conditions. Doctoral dissertation. Technische Universität
De Schepper SC, Heynderickx GJ, Marin GB (2008) CFD modeling of all gas–liquid and vapor–liquid flow regimes predicted by the Baker chart. Chem Eng J 138(1):349–357. https://doi.org/10.1016/j.cej.2007.06.007
Dokianos WP (2015) A simplified approach to sizing 2 and 3 phase separators for low GOR and low pressure onshore production batteries. In: SPE production and operations symposium. Society of Petroleum Engineers
Gas Processors and Suppliers Association (1998) GPSA engineering data book. GPSA, Tulsa
Gerunda A (1981) How to size liquid-vapor separators. Chem Eng 88(9):81–84
Ghaffarkhah A, Shahrabi MA, Moraveji MK, Eslami H (2017) Application of CFD for designing conventional three phase oilfield separator. Egypt J Pet 26(2):413–420. https://doi.org/10.1016/j.ejpe.2016.06.003
Gosman AD, Loannides E (1983) Aspects of computer simulation of liquid-fueled combustors. J Energy 7(6):482–490. https://doi.org/10.2514/3.62687
Hallanger A, Soenstaboe F, Knutsen T (1996) A simulation model for three-phase gravity separators. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Helsør T, Svendsen H (2007) Experimental characterization of pressure drop in dry demisters at low and elevated pressures. Chem Eng Res Des 85(3):377–385. https://doi.org/10.1205/cherd06048
Hernandez-Martinez JL, Martinez Ortiz V (2014) A method to size gas–liquid horizontal separators handling nonstable multiphase streams. In: SPE Latin America and Caribbean petroleum engineering conference. Society of Petroleum Engineers
Irani M, Bozorgmehry Boozarjomehry R, Pishvaie SMR, Tavasoli A (2010) Investigating the effects of mass transfer and mixture non-ideality on multiphase flow hydrodynamics using CFD methods. IJCCE 29(1):51–60
ISO 9377-2 (2000) Water quality- determination of hydrocarbon oil index—part2: method using solvent extraction and gas chromatography
Ivanova PG, Aneva ZV (2006) Assessment and assurance of quality in water measurement by coulometric Karl Fischer titration of petroleum products. Accredit Qual Assur 10(10):543–549. https://doi.org/10.1007/s00769-005-0056-x
Kestens V, Conneely P, Bernreuther A (2008) Vaporisation coulometric Karl Fischer titration: a perfect tool for water content determination of difficult matrix reference materials. Food Chem 106(4):1454–1459. https://doi.org/10.1016/j.foodchem.2007.01.079
Kharoua N, Khezzar L, Saadawi HN (2012) Using CFD to model the performance of retrofit production separators in Abu Dhabi. In: Abu Dhabi international petroleum conference and exhibition. Society of Petroleum Engineers
Kharoua N, Khezzar L, Saadawi HN (2013) CFD modelling of a horizontal three-phase separator: a population balance approach. Am J Fluid Dyn 3(4):101–118. https://doi.org/10.5923/j.ajfd.20130304.03
Kishan PA, Dash SK (2009) Prediction of circulation flow rate in the RH degasser using discrete phase particle modeling. ISIJ Int 49(4):495–504. https://doi.org/10.2355/isijinternational.49.495
Kister HZ (1990) Distillation operations. McGraw-Hill, New York City
Laleh AP, Svrcek WY, Monnery WD (2011) Computational fluid dynamics simulation of pilot-plant-scale two-phase separators. Chem Eng Technol 34(2):296–306. https://doi.org/10.1002/ceat.201000302
Laleh AP, Svrcek WY, Monnery WD (2012a) Computational fluid dynamics-based study of an oilfield separator-part I: a realistic simulation. Oil Gas Facil 1(06):57–68. https://doi.org/10.2118/161212-PA
Laleh AP, Svrcek WY, Monnery WD (2012b) Design and CFD studies of multiphase separators—a review. Can J Chem Eng 90(6):1547–1561. https://doi.org/10.1002/cjce.20665
Laleh AP, Svrcek WY, Monnery WD (2013) Computational fluid dynamics-based study of an oilfield separator-part II: an optimum design. Oil Gas Facil 2(01):52–59. https://doi.org/10.2118/161036-PA
Le AD, Zhou B (2008) A general model of proton exchange membrane fuel cell. J Power Sources 182(1):197–222. https://doi.org/10.1016/j.jpowsour.2008.03.047
Lu Y, Lee JM, Phelps D, Chase R (2007) Effect of internal baffles on volumetric utilization of an FWKO—a CFD evaluation. In: SPE annual technical conference and exhibition. society of petroleum engineers
Ludwig EE (1997) Applied process design for chemical and petrochemical plants. Gulf Professional Publishing, Texas
Lyons WC, Plisga GJ (2011) Standard handbook of petroleum and natural gas engineering. Gulf Professional Publishing, Texas
Mabrouk PA, Castriotta K (2001) Moisture analysis in lotion by Karl Fischer coulometry. An experiment for introductory analytical chemistry. J Chem Educ 78(10):1385. https://doi.org/10.1021/ed078p1385
Mahmud MA, Mazumder M, Xu Q, Khan RI (2018) Sloshing impact on gas pretreatment for LNG plants located in a stranded offshore location. Ind Eng Chem Res. https://doi.org/10.1021/acs.iecr.7b03631
Margolis SA, Hagwood C (2003) The determination of water in crude oil and transformer oil reference materials. Anal Bioanal Chem 376(2):260–269. https://doi.org/10.1007/s00216-003-1865-6
Monnery WD, Svrcek WY (1994) Successfully specify 3-phase separators. Chem Eng Prog 90(9):29–40
Moraveji MK, Hejazian M (2014) CFD examination of convective heat transfer and pressure drop in a horizontal helically coiled tube with CuO/Oil base nanofluid. Numer Heat Trans A Appl 66(3):315–329. https://doi.org/10.1080/10407782.2013.872976
Moraveji MK, Sabah M, Shahryari A, Ghaffarkhah A (2017) Investigation of drill pipe rotation effect on cutting transport with aerated mud using CFD approach. Adv Powder Technol 28(4):1141–1153. https://doi.org/10.1016/j.apt.2017.01.020
Morsi S, Alexander AJ (1972) An investigation of particle trajectories in two-phase flow systems. J Fluid Mech 55(02):193–208. https://doi.org/10.1017/S0022112072001806
Mpagazehe JN (2013) A physics-based, eulerian–lagrangian computational modeling framework to predict particle flow and tribological phenomena. Doctoral dissertation, Carnegie Mellon University
Mulyandasari V (2011) Separator vessel selection and sizing (engineering design guideline). KLM Technology Group, Malaysia
Newton CL (1976). U.S. Patent No. 3,997,303. U.S. Patent and Trademark Office, Washington, DC
Olotu CO, Osisanya S (2013) Development of a user friendly computer program for designing conventional oilfield separators. In: SPE Nigeria annual international conference and exhibition, Society of Petroleum Engineers
Ounis H, Ahmadi G, McLaughlin JB (1991) Brownian diffusion of submicrometer particles in the viscous sublayer. J Colloid Interface Sci 143(1):266–277. https://doi.org/10.1016/0021-9797(91)90458-K
Patankar S (1980) Numerical heat transfer and fluid flow. CRC Press, Boca Raton
Patankar SV, Spalding DB (1972) A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int J Heat Mass Transf 15(10):1787–1806. https://doi.org/10.1016/0017-9310(72)90054-3
Peyret R (1996) Handbook of computational fluid mechanics. Academic Press, Nice
Raoufi A, Shams M, Farzaneh M, Ebrahimi R (2008) Numerical simulation and optimization of fluid flow in cyclone vortex finder. Chem Eng Process 47(1):128–137. https://doi.org/10.1016/j.cep.2007.08.004
RosIN P (1933) The laws governing the fineness of powdered coal. J Inst Fuel 7:29–36
Shaban HI (1995) A study of foaming and carry-over problems in oil and gas separators. Gas Sep Purif 9(2):81–86. https://doi.org/10.1016/0950-4214(95)93944-F
Shukla SK, Shukla P, Ghosh P (2011) Evaluation of numerical schemes for dispersed phase modeling of cyclone separators. Eng Appl Comput Fluid 5(2):235–246. https://doi.org/10.1080/19942060.2011.11015367
Smith H (1987) Oil and gas separators. Petroleum engineering handbook. SPE, Richardson
Stanley W, Walas E (1990) Chemical process equipment-selection and design. Butterman-Heinemam Series, Massachusetts
Stewart M, Arnold K (2008) Gas-liquid and liquid-liquid separators. Gulf Professional Publishing, Texas, USA, Gulf Equipment Guides
Sun X, Wang K, Yan T, Shao S, Jiao J (2014) Effect of drill pipe rotation on cuttings transport using computational fluid dynamics (CFD) in complex structure wells. J Petrol Explor Prod Technol 4(3):255–261. https://doi.org/10.1007/s13202-014-0118-x
Vilagines RD, Akhras AR (2010) Three-phase flows simulation for improving design of gravity separation vessels. In: SPE annual technical conference and exhibition, Society of Petroleum Engineers
Viles JC (1993) Predicting liquid re-entrainment in horizontal separators. J Petrol Technol 45(05):405–409. https://doi.org/10.2118/25474-PA
Wang F, Tan J, Wang Z (2014) Heat transfer analysis of porous media receiver with different transport and thermophysical models using mixture as feeding gas. Energy Convers Manag 83:159–166. https://doi.org/10.1016/j.enconman.2014.03.068
Watkins R (1967) Sizing separators and accumulators-speed with which operators can correct upsets is included in these design considerations. Hydrocarbon Process 46(11):253
Wilcox DC (1993) Turbulence modeling for CFD, vol 2. DCW industries, La Canada CA
Xu Y, Liu M, Tang C (2013) Three-dimensional CFD–VOF–DPM simulations of effects of low-holdup particles on single-nozzle bubbling behavior in gas–liquid–solid systems. Chem Eng J 222:292–306. https://doi.org/10.1016/j.cej.2013.02.065
Yang M (2011) Measurement of oil in produced water. In: Lee K, Neff J (eds) produced water. Springer, New York, pp 57–88. https://doi.org/10.1007/978-1-4614-0046-2_2
Zakerian A, Sarafraz S, Tabzar A, Hemmati N, Shadizadeh SR (2018) Numerical modeling and simulation of drilling cutting transport in horizontal wells. J Petrol Explor Prod Technol. https://doi.org/10.1007/s13202-018-0435-6
Zhang L (2009) Three-dimensional numerical modeling of hydrodynamic flow. Sediment deposition and transport in stormwater ponds and alluvial channels. Doctoral dissertation, Old Dominion University
Zhang Z, Chen Q (2009) Prediction of particle deposition onto indoor surfaces by CFD with a modified Lagrangian method. Atmos Environ 43(2):319–328. https://doi.org/10.1016/j.atmosenv.2008.09.041
Zhang Z, Zhang W, Zhai ZJ, Chen QY (2007) Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: part 2—comparison with experimental data from literature. Hvac&R Res 13(6):871–886. https://doi.org/10.1080/10789669.2007.10391460
Zhao B, Yang C, Yang X, Liu S (2008) Particle dispersion and deposition in ventilated rooms: testing and evaluation of different Eulerian and Lagrangian models. Build Environ 43(4):388–397. https://doi.org/10.1016/j.buildenv.2007.01.005
Acknowledgements
The authors thank NIOC for permission to publish these data. We would also like to thank Dr. Nasiri A. (Research Institute of Petroleum Industry) for his valuable discussion in the experimental part of this work. The authors also thank the anonymous referees for comments on this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ghaffarkhah, A., Dijvejin, Z.A., Shahrabi, M.A. et al. Coupling of CFD and semiempirical methods for designing three-phase condensate separator: case study and experimental validation. J Petrol Explor Prod Technol 9, 353–382 (2019). https://doi.org/10.1007/s13202-018-0460-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-018-0460-5