Accounting for diagenesis overprint in carbonate reservoirs using parametrization technique and optimization workflow for production data matching

Abstract

Diagenesis is rarely accounted for in the standard modeling workflows for carbonate reservoirs, although it has a huge impact on both porosity and permeability. This can be explained by at least two reasons: first, it is difficult to quantify the influence of diagenetic overprints on porosity and permeability; second, the integration of the diagenetic effects in carbonate reservoir models makes history matching much more difficult. Herein, a modeling methodology is proposed, in which the diagenetic imprints are included in the reservoir model and calibrated with dynamic data. The key point consists in defining a parametrization technique able to capture these diagenetic imprints. We assume that distinct regions of occurrence of a given diagenetic phase can be identified within the reservoir. Therefore, restricting our attention to a facies, we may distinguish regions characterized by low, medium or high proportions of the targeted diagenetic phase. The advantage of this parametrization technique is that the proportions of these regions can be easily driven by a reduced number of proportionality coefficients. Then, the overall modeling approach is integrated in an optimization workflow making it possible to vary the proportions of the region with a given occurrence for a given diagenetic phase, the variograms characterizing the spatial distribution of the regions, or even the way they are spatially distributed. The optimization process is run to adjust these various unknown parameters in order to match production history. The potential of the proposed methodology is finally investigated through the study of a two-dimensional numerical example.

Introduction

Carbonate reservoirs exhibit complex pore systems, which depend on their biological origin and great chemical reactivity (Flugel 2010; Moore 2001). The geometry and connectivity of these pores strongly control the dynamic flow of hydrocarbons in carbonate reservoirs. As more than 60% of the world’s oil and 40% of the world’s gas reserves are estimated to be held in such reservoirs, the oil and gas industry looks constantly to improve the representation of carbonate reservoirs through geological and simulation models that better capture and illustrate their heterogeneities. The standard reservoir modeling workflow consists in integrating seismic, geological and well data to create a static geological model. This one is usually populated by facies or lithofacies and their associated petrophysical properties like porosity, permeability and fluid saturations (Deutsch 2002). The static model is then inputted into a fluid flow simulator in order to understand fluid displacements and forecast production over reservoir lifetime.

In the current industry practice, diagenesis is generally integrated through the definition of lithofacies referring to textures and pore systems or rock types. However, this approach cannot be easily applied through history matching and field development optimization, because diagenesis imprint has not been modeled and thus cannot be modified according to production data. Moreover, even when taken into account, it is most of the time through a deterministic approach with a limited number of models. Due to the uncertainty in the description of the occurring diagenesis phases and their effects in the facies deposition model, a stochastic framework may be preferred. Several authors (Barbier et al. 2012; Doligez et al. 2011; Hamon et al. 2015; Labourdette et al. 2007) investigated and applied geostatistical methods to integrate depositional facies and diagenetic overprint models. The leading idea consists first in identifying the major diagenetic phases, which modify the petrophysical properties and second in qualitatively or semiquantitatively establishing the relationship linking the diagenetic phases to the depositional facies. The first identification step is usually performed from the analysis of thin sections and laboratory measurements of core samples. It is based upon the definition of the paragenetic sequence, which is a conceptual representation of the diagenetic events through time. The paragenetic sequence permits to schematically display the relationships between these diagenetic phases and the resulting porosity and permeability modifications (Moore 2001). The second step yields the relationships between the diagenetic phases and the depositional facies from petrographic observations. When this information is available, it can be integrated into reservoir models, provided that suitable stochastic simulation techniques are applied. For instance, Renard et al. (2008) extended the well-known pluriGaussian simulation (PGS) technique (Le Loc’h et al. 1994) to get the bivariate pluriGaussian simulation (Bi-PGS) one. Such a method makes it possible to populate reservoir models with spatially varying facies and to account for diagenetic phases with spatially varying influences on facies. Even though data are provided through the analysis of thin section or laboratory measurements, they represent a very tiny part of the actual reservoir under consideration. Upscaling of diagenesis characteristics, but also of petrophysical properties like porosity and permeability, is still a major issue. Even when properties and relationships between facies and diagenesis have been clearly identified at the plug scale, the question remains about the corresponding properties to be provided to the grid cells of the reservoir model, which is associated with a much larger scale with macro-porosity occurrences, locally baffling heterogeneities, fractures, etc. (Farooq et al. 2014; Nader et al. 2013). This is all the more true for diagenetized carbonate reservoir (Benyamin 2016).

The resulting static reservoir model is therefore very uncertain. The integration of other sources of information is required to better constrain the reservoir models used to represent the real one. This is why production data are also considered. They consist of all the data measured at wells during production: pressures, flow rates, gas/oil ratios, water cuts. The integration of production data into a static reservoir model is known as history matching (Jacquard and Jain 1965). This usually involves the definition of an objective function, which measures the least-square differences between the actual production data and the corresponding numerical responses simulated for the considered static model using a flow simulator. Then, an optimization process is run aiming at minimizing the objective function by successively adjusting some uncertain parameters of the static reservoir model or the associated flow model. The interested reader may refer, for instance, to Le Ravalec et al. (2014) for more details. This calibration process contributes to improve the reservoir model, i.e., to make it more reliable for predictions and to better describe fluid flows within the reservoir. The most valuable result is the capacity to predict reservoir production lifetime with a certain level of confidence and to evaluate its economic potential. One of the fundamental aspects of history matching is parameterization. A reservoir model and its associated flow features include a huge number of unknown or uncertain parameters. For instance, the flow characteristics depend on the definition of fault transmissivities, relative permeability and capillary pressure curves, coefficients describing the strength of the aquifers. On the other hand, the reservoir model itself consists of a grid that has to be populated by facies, porosity values, permeability values and initial saturations. The large number of uncertain parameters and the need for preserving geological consistency all along the history-matching process steered the development of specific parameterization techniques. The gradual deformation method (Hu 2000) and the probability perturbation method (Caers and Hoffman 2006) were then proposed to adjust the spatial distributions of facies and petrophysical properties from a reduced number of auxiliary parameters. In addition, they permit to preserve the spatial variability model inferred from the static data whatever the variations in the auxiliary deformation parameters. Other parameterization techniques were designed for handling facies proportions; Ponsot-Jacquin et al. (2009) introduced a very simple and intuitive method that involves proportionality coefficients to drive the variations in the different facies proportions. A drawback of the method was the discontinuities occurring on the boundaries of the regions submitted to modifications. An improved kriging-based approach was then suggested by Tillier et al. (2010) to remove these undesired boundary effects. A preliminary tentative for integrating diagenesis effects into history matching was described by Pontiggia et al. (2010), but the approach was based upon screening, not on the iterative minimization of an objective function. There was no dedicated parameterization technique for diagenesis.

In this paper, we focus on the development of a simulation workflow making it possible to integrate diagenesis information in the generation of the static model and to consistently modify this model to also account for production data. In our case, “consistently” means that we want to be able to calibrate the model to the production data while preserving its geological characteristics derived from the analysis of static data, of which diagenesis. All of this actually calls for the definition of a new parameterization technique for driving diagenesis description. The one proposed hereafter is rooted in the approach developed by Ponsot-Jacquin et al. (2009) for varying facies proportions. Section 2 describes the overall simulation workflow including the step especially added for diagenesis. In this section, the potential of the methodology is investigated on the basis of a synthetic case with three depositional facies. Finally, the third section focuses on sensitivity analysis and shows how the diagenetic modeling parameters influence the reservoir dynamic response.

Geological and reservoir simulation approach

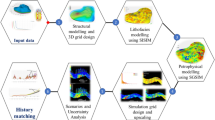
The usual simulation workflow includes two main steps (Fig. 1). The first one is the stochastic simulation of the static reservoir model with the generation of facies and then the distribution of petrophysical properties. The second step entails fluid flow simulation. When this workflow is built, an optimization process can be run that successively varies any of the uncertain parameters involved in the simulation workflow. The methodology proposed in this paper considers diagenesis as an additional block at the level of the static geological model prior to reservoir modeling. Thus, the parameters defined within this block can be also updated to fit the production data following the calculations performed by the optimizer.

Fig. 1

Overall simulation workflow. Optimization can be applied to calibrate the parameters involved in any of the different blocks of the simulation workflow

To get the static reservoir model, we start generating facies, and then, we simulate the diagenesis phases given the facies before going through the distribution of the petrophysical properties. This process is described in the first part of this section. The key point consists in defining a simple and easy to use parametrization technique able to capture these diagenetic overprints. We assume that distinct regions can be identified within the reservoir depending on the occurrence of given diagenetic phases. For instance, we may distinguish regions within a facies, which are characterized by low, medium or high proportions of a targeted diagenetic phase.

Once the facies and the associated diagenesis imprint models are built, the facies is populated with porosity and permeability properties. Then, it is inputted into a fluid flow simulator to calculate dynamic flow responses that can be compared to the actual production data. The least-square differences between data and synthetic responses yield the objective function. The purpose of history matching consists in adjusting the unknown parameters everywhere to minimize the objective function: when generating facies (spatial distributions, variograms and proportions), when distributing the diagenetic phases (spatial distributions, variograms and proportions), when generating the petrophysical properties (spatial distributions, variograms and means) and when simulating fluid flow (aquifer strength, fault transmissivities, PVT, etc.). The optimization process applied in this paper is presented in the second part of this section. For simplicity, we focus on the parameters related to the simulation of the diagenetic phases. However, the generalization to any block of the simulation workflow is straightforward.

Diagenesis model definition

As explained above, the generation of a static model calls first for the simulation of facies, second of diagenesis phases, and last of petrophysical properties. However, a preliminary mandatory step is the definition of the relationships between the facies and diagenetic phases. The diagenetic phases are produced under specific conditions by physical, chemical and biological processes: they locally modify the petrophysical properties of facies. The most common diagenetic processes in carbonate reservoirs are micritization, dissolution, cementation, dolomitization and replacement of carbonate grains (Moore 2001). A preliminary step before going through modeling is characterization, which means description and classification of lithofacies. A wide range of analytical techniques can be used to study carbonate diagenesis (Gasparrini et al. 2006; Nader et al. 2004): conventional petrographic studies combined with cathodoluminescence, fluorescence, scanning electron microscopy, micro-CT, but also geochemical studies and fluid inclusion analyses. Description of diagenesis is usually qualitative. However, we can also perform a semiquantitative analysis by visual observation or point counting on thin sections. This makes it possible to determine how much a diagenetic P phase affects a given A facies. For instance, it can be observed that the occurrence of phase P in facies A is moderate. In addition, non-stationarity has also to be accounted for. The occurrence of phase P may spatially vary. It can be moderate in some regions, low or high in others. Clearly, a facies may be affected by several diagenetic phases. The information resulting from the characterization study is recapped in a table such as Table 1. In this example, there are three facies: A, B and C. Focusing on facies A, the overprints of three diagenetic phases are evidenced. The first one, named Phase 1, occurs with high level in 80% of facies A and moderate level in the 20% remaining. Such a representation permits to approximate the complexity of the diagenesis overprints in a carbonate reservoir.

Table 1 Quantitative relationships between facies A, B, C and diagenetic phases P1, P2, P3

Sedimentary facies modeling

Various geostatistical algorithms can be applied to randomly produce facies models. They can be split into three main groups with two-point statistics pixel-based methods, multiple-point statistics pixel-based ones and object-based ones. In this paper, we focus on the truncated Gaussian simulation (TGS) technique, which belongs to the first group. It is used to generate a spatial categorical variable (Matheron et al. 1987) by simulating and truncating a Gaussian random function (GRF). This widely used approach exhibits a special feature that may be undesired in some cases: the generated facies respect a sequential ordering. However, this limitation is easily overcome with pluriGaussian simulation, which involves the truncation of at least two Gaussian random functions (Le Loc’h et al. 1994). For simplicity, the description below is restricted to TGS.

Let us consider a standard GRF, named Y_i(x), with i ∈ [1, n] and n the number of facies. It is truncated by one or more thresholds in order to generate a series of indicators I_i(x) representing the F_i(x) facies:

$$F_{i} = \left\{ {x \in R;\quad {\text{if}}\; y_{i - 1} < Y\left( x \right) \le y_{i} } \right\}$$

(1)

$$I_{i} \left( x \right) = \left\{ {\begin{array}{*{20}l} {1, \quad {\text{if}}\; y_{i - 1} < Y\left( x \right) \le y_{i} } \\ {0,\quad {\text{otherwise}}} \\ \end{array} , } \right.\quad - \infty , = y_{0} < y_{1} < \cdots , < y_{i - 1} < y_{i} < \cdots < y_{n + 1} = + \infty$$

The I_i(x) indicators equal 1 when the values of Y_i(x) belong to the interval defined by thresholds y_i-1 and y_i. This interval is associated with facies F_i(x).

The (y_i) thresholds are estimated to match the indicator proportions (p_i) from the following equation:

$$y_{i} = G^{ - 1} \left( {\mathop \sum \limits_{j = 1}^{i} p_{j} } \right), \quad i = 1, \ldots , n - 1$$

(2)

where G is the normal standard cumulative density function. Thus, we first simulate a realization of Y and turn it into a facies realization by applying the (y_i) thresholds. A two-dimensional example is shown in Fig. 2. This realization includes three facies with identical proportions.

Fig. 2

Truncated Gaussian simulation with a the realization of a Gaussian random function; b the resulting facies realization after applying truncation; c the threshold mask

Diagenesis modeling

Once the facies model has been generated, the second stage of the proposed methodology is the modeling of the diagenetic phases inside facies, which is achieved again using a stochastic approach. The diagenetic phases are also represented by categorical variables. In addition, as explained above, the regions where a given diagenetic phase is observed may be split into subregions depending on the levels of occurrence, for instance, low (L), medium (M) and high (H). These distinct levels are also considered as categorical variables. To model the spatial distribution of these various levels of occurrence, we refer to the Bi-pluriGaussian simulation (Bi-PGS) as introduced by Renard et al. (2008). On the one hand, the facies model is generated from a PGS model, or for simplicity from a TGS model. On the other hand, the diagenetic phase model is derived from another PGS model, or for simplicity from another TGS model. The link between the two PGS or TGS models is driven by a proportion table similar to Table 1. An example, inspired by Renard et al. (2008), is displayed in Fig. 3. A carbonate formation is assumed to include three sedimentary facies (A, B and C) that were differently submitted to the same diagenetic process. This resulted in a single diagenetic phase occurring following three levels in facies A (levels low, medium and high), two levels in facies B (levels low and medium) and 1 level (low) in facies C. The proportions for each occurring bivariate associations (A-L; A-M; A-H; B-L; B-M; C-L) are all equal to 1/6. The proportion for any other association is 0. We first refer to TGS to simulate the facies realization. This explains why the threshold mask for facies is made of parallel rectangles. Then we use another TGS model to populate facies A and B with the required diagenetic levels. As facies C contains a single level of the diagenetic phase under consideration, there is no need to apply truncation in this facies. Again, the threshold mask for the diagenetic levels is formed of parallel rectangles because of the use of the TGS method.

Fig. 3

Bi-TGS Application: a Realization with facies A, B and C; b Realization with diagenetic levels L, M and H. The color lines indicate facies boundaries. c Threshold mask for facies and for diagenetic levels inside facies A and B

Petrophysical property modeling

As mentioned previously, the facies and diagenetic overprints are categorical variables that represent specific petrophysical rock characteristics. The last step of the static modeling workflow deals with the simulation of porosity, permeability and fluid saturation properties to populate the diagenetic levels. Distinct simulations algorithms can be applied to do so of which Sequential Gaussian Simulation (Goovaerts 1997) or Fast Fourier Transform Moving Average (Le Ravalec et al. 2000).

Reservoir modeling and history matching

When the static model is built, it can be inputted into a fluid flow simulator to get numerical production responses, such as pressures or fluid rates at wells. This last block of the overall simulation workflow is said dynamic since the production responses vary with time.

The purpose of history matching is to adjust any uncertain parameters involved in the simulation workflow to force the numerical production responses to reproduce as well as possible the production data collected at wells. The data mismatch is quantified from an objective function defined as:

$$J\left( {{\mathbf{param}}} \right) = \frac{1}{2}\mathop \sum \limits_{m = 1}^{M} \omega_{m} (f_{m} \left( {{\mathbf{param}}} \right) - f_{m}^{obs} )^{2}$$

(3)

J is the objective function. It depends on vector param that includes all the parameters defining the static and dynamic models. Vectors f^obs and f are the measured production data and the corresponding production responses simulated for the parameters included in param, respectively. The ω_m coefficients are weights assigned to the measured production data f ^obs _m with m = 1,…,M, where M is the number of available production data. The determination of param given the production data is an ill-posed inverse problem, meaning that there may be several solutions or no solutions at all and that the solution may be very sensitive to slight fluctuations in the production data. It is usually solved on the basis of an optimization process run to minimize the objective function. In a nutshell, the parameters are sequentially adjusted until the objective function is small enough. Any time a parameter is changed; a fluid flow simulation is run to compute the updated production responses. This process can be time-consuming as it may call for a large number of iterations. The uncertain parameters can belong to any of the blocks of the simulation workflow. There can be of different types. There are scalar parameters like the proportions of a facies provided it is stationary, but also stochastic spatial parameters like porosity values. The perturbation in these stochastic parameters cannot be performed anyhow, and specific parameterization techniques have been developed to handle this issue. One of them is the gradual deformation method (Hu, 2000). The basic principle consists in combining two independent Gaussian random functions, Y_o and U, with identical mean m and covariance function C:

$$Y\left( t \right) - m \, = \left( {Y_{o} {-} \, m} \right)\cos (\pi t) + \left( {U{-}m} \right)\sin (\pi t)$$

(4)

In such conditions, it can be shown that Y is also a Gaussian random function of mean m and covariance C whatever the value of the t deformation parameter. This property holds because the two Gaussian random functions are independent and because the sum of the squares of the coefficients applied to the two Gaussian random functions equals 1. Let us consider a realization y_o of Y_o and a realization u of U. y_o can be considered as the initial guess for the static model and u as a random complementary realization. For simplicity, the mean of the two Gaussian random functions is assumed to be 0. When the t deformation parameter is 0, the equation above yields a y realization identical to y_o. When t is 0.5, it leads to u. When t gradually varies from 0 to 0.5, the y realization is smoothly modified to evolve from y_o to u. This is why the deformation process is said gradual: it makes it possible to slightly and continuously change the y realization. The whole process is periodic with t varying in [− 1, 1]. When this parametrization technique is included into the minimization process, the purpose is to catch the y realization or equivalently the t deformation parameter that provides the smallest value for the objective function. Clearly, the chain of realizations built by varying t represents a very tiny part of the entire search space. Therefore, the complete gradual process consists in successively investigating different chains of realizations. The first one is produced from initial guess y_o and realization u. A first minimization process is run to explore this first chain and to determine the realization associated with the smallest objective function. This realization is said to be the first optimal one. Then, we replace y_o with the first optimal realization and randomly draw a new u realization. This provides a second chain of realizations. We can restart the minimization process to investigate this new chain and identify a new optimal realization, which permits to decrease further the objective function. The minimization loops are repeated until the data misfit is small enough.

A few authors (Roggero and Hu 1998; Thomas et al. 2005; Tillier et al. 2010) showed that the gradual deformation process can be also used to perturb the realizations of categorical variables and match well production.

Reference case

The methodology described above is applied to a synthetic case to evaluate its potential. First, we built a reference case populated with facies, diagenetic phases, and petrophysical property distributions.

The reference case is associated with a two-dimensional grid including 200 × 200 × 1 blocks whose size is 5 × 5 × 5 m³ for each. The reservoir was assumed to consist of three sedimentary facies named facies A, facies B and facies C (Fig. 3, a). Their proportions were set to 0.5, 0.33 and 0.17, respectively. Their spatial variabilities were characterized by an anisotropic Gaussian variogram with a range of 600 m along the main axis, this one being defined by an azimuth of 45°. The range along the perpendicular axis was 120 m. The truncated Gaussian method was then used to generate the facies model.

The principal diagenetic process that altered facies A was silicification. This phase was characterized by three levels with occurrences defined as low, medium and high. The corresponding proportions were 0.15 for the low level, 0.21 for the medium one and 0.64 for the high one. Silicification contributed to reduce porosity and permeability in different degrees as listed in Table 2. On the other hand, facies B was mainly affected by calcite cementation according to two levels of occurrence defined as low and medium. The two levels occurred with identical proportions. This diagenetic phase occluded the pore space and reduced connectivity when its proportion was high. Finally, facies C was fully silicified (high level of occurrence only) so that its porosity and permeability properties were very low.

Table 2 Characteristics of diagenesis per facies: proportions, porosities and permeabilities

The diagenetic phases were then distributed inside each facies still referring to the truncated Gaussian method. In this case, the variogram describing the spatial variability of diagenesis was an isotropic Gaussian one with a range of 600 m. The resulting diagenesis model is displayed in Fig. 4a. Constant porosity and permeability values were then assigned to each of the diagenesis levels (Table 2). This hypothesis was considered so that we can focus on the calibration of the diagenesis parameters. The ultimate reference porosity and permeability models are shown in Fig. 5. We check that, for this case, the more significant the diagenesis, the lower the permeability and the porosity.

Fig. 4

a Reference diagenetic model (DM1). b Starting diagenetic model. c Final diagenetic model. The lines overimposed on the figure indicate the boundaries of the facies

Fig. 5

Reference case—porosity and permeability

This reference porosity and permeability model was then inputted into a flow simulator to calculate production responses that will be assimilated to reference production data in a subsequent step. A vertical injecting well was set up in the lower left corner of the two-dimensional grid, and a vertical producing well was also set up in the opposite corner. Water was then injected at 200 m³/day. A constant flow rate of 200 m³/day was considered at the producer. The relative permeability curves were given by Corey’s model with an exponent of 2. The water and oil viscosities were fixed to 1. The water cut obtained at the producer is given in Fig. 6b. It is characterized by a breakthrough time of about 1500 days. For illustration purposes, the water saturations at breakthrough time are shown in Fig. 6a. They clearly show the influence of diagenesis heterogeneities.

Fig. 6

a Water saturation map at breakthrough time. b Reference water cut

Diagenesis modeling

Parameterization of diagenetic proportions

As mentioned above, we aim at adjusting diagenesis from production data by varying the variograms considered for simulating the diagenetic phases, their spatial distributions, but also their proportions. The variograms involve scalar parameters such as the range that can be perturbed using any usual minimization algorithm. The variations in the spatial distributions can be driven by the gradual deformation method as explained in Sect. 2.5. The issue that still has to be solved is about the proportions of the various diagenetic phases, but also the proportions of the distinct levels of occurrence for a given diagenetic phase. All of these proportion values that have to be calibrated finally lead to a significant number of parameters. In this section, we introduce a new parameterization technique to vary all diagenetic proportions from a reduced number of proportionality coefficients. This will contribute to ease the ultimate optimization process.

For illustrative purposes, we restrict our attention to a case with one diagenetic phase characterized by three levels of occurrence: high (H), medium (M) and low (L). A single a parameter is then defined to vary the proportions of any of the occurrence levels. The idea consists in splitting the diagenetic levels into two groups whose proportions evolve following the same trend inside each group. For the example studied, we separate level L from levels M and H. Thus, parameter a becomes the proportions of level L. If a increases, the proportion of L increases, while those of M and H proportionally decrease (Fig. 7). This holds because the sum of the three proportions is 100%.

Fig. 7

Example illustrating the impact of parameter a. Parameter a controls the proportions of the level of low occurrence of the targeted diagenetic phase in facies A

The proportions of the three diagenetic levels are modified depending on parameter a. The new proportions for levels L, M and H are given by:

$$pL_{new} = a$$

$$pM_{new} = \left( {\frac{{1 + \left( {pL_{0} - a} \right)}}{{pM_{o} + pH_{0} }}} \right) \times pM_{0}$$

(5)

$$pH_{new} = \left( {\frac{{1 + \left( {pL_{0} - a} \right)}}{{pM_{o} + pH_{0} }}} \right) \times pH_{0}$$

pL, pM and pH stand for the proportions of the L, M and H diagenetic levels. Subscripts 0 and new are used to discriminate the initial and modified proportions, respectively.

This parameterization technique can be included into the optimization process described in Sect. 2.2. Then, a is viewed as an additional parameter to be determined from the minimization of the objective function. It is handled as any other scalar parameters. The methodology can become as complex as the diagenetic depositional conceptual model is. Several diagenetic phases affecting in different extents the carbonate reservoir can be considered. The interest of this new approach is the decrease in the number of parameters: the whole set of diagenetic proportions can be driven from one or a few proportionality a parameters.

Influence of variograms

The starting reservoir model, denoted DM1, is the one shown in Fig. 4a. It was built using the TGS version of the Bi-PGS method. The two-dimensional grid that serves as a basis for the model consists of 200 × 200 × 1 grid blocks. The dimensions of each grid block are 1 × 1 × 1 m³. The variogram of the Gaussian random function used to simulate the diagenetic levels is Gaussian, anisotropic with a range of 20 grid blocks along the main axis that is the diagonal one. This model contains three facies, each differently modified by the same diagenetic phase. The regions defined by a given level of occurrence of the diagenetic phase in a given facies are attributed constant and identical petrophysical properties. This means that levels L in facies A and facies B have distinct porosity and permeability values. In a given facies, the rule followed is that the stronger the diagenesis impact or the occurrence of the diagenetic phase, the lower the porosity and permeability values. In a second step, we keep all parameters identical except the range along the main axis. It is now reduced to 10 grid blocks. The two diagenesis models are compared in Fig. 8.

Fig. 8

a Diagenetic model DM1 with a variogram range of 20 m. b Diagenetic model DM2 with a variogram range of 10 m. The lines overimposed on the figures indicate the boundaries of the facies

The extension of diagenesis over facies can be evaluated. Increasing the variogram range contributes to create large connected areas of fair reservoir quality like the areas in blue. On the other hand, the decrease in the variogram range produces less connected regions and consequently creates more tortuous flow path. To evidence the impact on fluid displacement, we assume that the reservoir is produced by injecting water at the bottom left corner. This makes it possible to push oil toward the producer that is in the top right corner. Saturation maps at breakthrough for DM1 and DM2 models are shown in Fig. 9a and b. The water cuts obtained for these two models are displayed in Fig. 9c. In this case, we note that varying the range has almost no impact on water cuts.

Fig. 9

a Saturation map for DM1 model at breakthrough. b Saturation map for DM2 model at breakthrough. c Water cuts simulated for DM1 (red) and DM2 (blue)

Influence of the spatial distribution

The purpose of this subsection is to stress the influence of the spatial distribution of the diagenetic levels on fluid flow. We actually refer to the gradual deformation method to vary this spatial distribution. This implies a variation in the gradual deformation parameter (Eq. 4), all other parameters being fixed. Three diagenetic models, DR1, DR2 and DR2, were generated by setting a gradual deformation parameter of 0, 0.5 and 1, respectively. The resulting changes in the diagenesis models are shown in Fig. 10. Their impacts on fluid flow are evidenced by the water cuts in Fig. 11. This time, the variations in the spatial distributions of the diagenetic heterogeneities lead to different water cut curves. The breakthrough times evolve from 1200 to 1500 days.

Fig. 10

a DR1 with gradual parameter of 0. b DR2 with gradual parameter of 0.5. c DR3 with gradual parameter of 1. The lines overimposed on the figures indicate the boundaries of facies

Fig. 11

a DR1 (t = 0) saturation map at breakthrough. b DR2 (t = 0.5) saturation map at breakthrough. c DR3 (t = 1) saturation map at breakthrough. d Water cuts simulated for DR1 (red), DR2 (blue) and DR3 (black)

Influence of level proportions

Finally, we investigate the effect of the proportions of the diagenetic levels. We generate two diagenetic models applying the TGS method with identical variograms. The only differences result from the proportions of high, medium and low levels in facies A. For the other facies, the proportions are kept. For the first model, DP1, the level proportions in facies A are defined as 0.1 for low, 0.4 for medium and 0.5 for high. For the second model, DP2, these proportions are set to 0.8 for the low level, 0.1 for the medium one and 0.1 for the high one (Fig. 12). The corresponding simulated water cuts are reported in Fig. 13. We observe that the proportions of the levels of occurrence of the diagenetic phase significantly affect the fluid flow. The two water cut curves are very different with breakthrough times varying from about 1300–2300 days.

Fig. 12

a Diagenetic model DP1. b Diagenetic model DP2. The lines overimposed on the figures indicate the boundaries of the facies

Fig. 13

a Saturation map for DP1 model at breakthrough. b Saturation map for DP2 model at breakthrough. c Water cuts simulated for DP1 (red) and DP2 (blue)

History matching: calibrating diagenesis from dynamic data

At this stage, the purpose is to see whether the proposed history-matching procedure makes it possible to calibrate diagenesis from the available dynamic or production data. For the numerical experiment under consideration, we now assume that everything about the static reference model is known except the parameters characterizing silicification in facies A. In other words, the spatial distribution of silicification heterogeneities as well as the proportions of the regions associated with the low, medium and high levels of occurrence is unknown. The issue to be investigated is about the possibility to calibrate this diagenetic phase from the reference water cut data provided in Fig. 6b. The matching process described in Fig. 1 is then run with unknown parameters in the diagenesis modeling block only. Two parameterization techniques are applied to drive the diagenesis model. The diagenesis proportion perturbation method proposed in this paper is considered to vary the proportions, while the gradual deformation method permits to change the spatial distribution of the diagenesis heterogeneities. This thus calls for the definition of two parameters: parameter a for the diagenesis level proportions and parameter t for the spatial distribution of diagenesis heterogeneities.

A given starting point, that is a given initial diagenesis model, is randomly generated (Fig. 4b). It is characterized by a seed that yields the heterogeneity distribution and a diagenesis proportion parameter a of 0.5. As in the example presented in Fig. 7, this a parameter gives at once the proportion of the region with a low occurrence level of silicification. This starting point is clearly different from the reference diagenesis model shown in Fig. 4, a: the value for the initial a parameter (0.5) is much larger than the one for the reference model (0.15).

The resulting porosity and permeability models are provided to the flow simulator to compute the water cut at the producer (Fig. 15). The resulting curve (black) is clearly different from the reference water cut (red curve) with a breakthrough time of 1750 days instead of 1500. The misfit is quantified by the objective function: its initial value is 0.34. Then, an optimized process is run to minimize this objective function by varying parameters a and t. A sketch of the approach followed is given in Fig. 14:

Fig. 14

Flowchart with the steps followed to minimize the objective function

• Step 1 generate the facies model, define parameter a and generate Y₀, an initial Gaussian white noise (see Eq. 4),

• Step 2 generate U, a complementary Gaussian white noise,

• Step 3 enter the gradual deformation loop that drives the t deformation parameter,

  • a. Combine Y_o and U to obtain Y.

  • b. Generate the diagenesis model.

  • c. Populate the resulting model with petrophysical properties.

  • d. Run the flow simulation.

  • e. Calculate the objective function.

  • f. Adjust parameters t and a.

  • g. Go back to 3(a) until convergence.

• Step 4 update Y₀ using the previous optimal Y and go back to step 2 until convergence.

Following this scheme, there are actually two loop levels. There is an inner loop that includes steps 3(a) to 3(g). At this level, U is fixed, while t and a vary. The purpose of this loop is to identify parameters t and a so as to minimize the objective function. As U is fixed, a tiny part only of the search space is investigated. This is why there is a second-level loop that groups steps 2, 3 and 4. This makes it possible to consider other U realizations, to build other chains of realizations and to explore further the search space.

The stopping criterion is defined as 10% of the initial objective function: when the objective function gets smaller than this value or when it is a value almost constant, the optimization process is stopped. The algorithm used for minimizing the objective function in step 3 is Simulated Annealing (Kirkpatrick et al. 1983). Its name comes from the annealing process in metallurgy, a technique with first heating and then cooling under a controlled temperature. The idea behind is to reach an equilibrium state corresponding to a global optimum. Given a starting point, the algorithm considers a random parameter perturbation and calculates the resulting change in the system energy (i.e., objective function). If this system energy decreases, the perturbation proposed is accepted. If it increases, the perturbation is accepted following a given probability. This prevents the algorithm from getting stuck in local minima. Perturbations are repeated until the system energy reaches a steady state or complies with the stopping criterion.

The first attempt performed required three second-level loops before satisfying the stopping criterion. The water cut curve simulated for the final model can be compared to the reference data in Fig. 15. Slight differences can be observed, but the general behavior is captured. The final objective function value was 2% of its initial value. It was reached for a parameter a of 0.22 that evolves the right way as it gets close to its reference value (0.15). In addition, we checked that the t value strongly varies all along the minimization process, which means that the spatial distribution of diagenesis heterogeneities has a significant effect on the history matching. It is also worth comparing the final diagenesis model (Fig. 4c) with the reference one (Fig. 4a): the main diagenesis heterogeneities are captured by the matching process.

Fig. 15

Water cuts for the reference case (red), the initial model (black) and the final one (blue)

The overall process was actually repeated 10 times to study the potential of this matching method. In other words, 10 different starting points were considered and the matching process was then run 10 times providing 10 matched models. The results obtained are recapped in Table 3 and Fig. 16. Table 3 points out that the a parameter decreases every time and tends toward the reference a value. The mean a matched value is 0.24, while the variance is 0.06. Another important feature is that the t deformation parameter changes a lot, which evidences the influence of the spatial distribution of diagenesis heterogeneities on production data and the potential of these data to better constrain diagenesis.

Table 3 Optimization results for 10 different initial points: initial and final objective function, optimal a parameter

Fig. 16

a Initial water cut profiles for 10 cases (dotted lines). b Water cut profiles for 10 matched cases (dotted lines). The reference water cut is the solid red line

Conclusions

We developed a methodology to calibrate diagenesis from production data. A diagenesis modeling step was added to classical modeling workflows, and a new, simple and intuitive parameterization technique was proposed to drive the proportions of the various levels for a given diagenetic phase. This made it possible to design a matching workflow aiming at calibrating the proportions, the spatial distribution and variability of the diagenetic phases on top of usual parameters.

A sensitivity study was then performed. It evidenced that the diagenesis modeling parameters such as the variogram range, the proportions and the spatial variability influence the simulated production responses to various extents. The proportions of the diagenesis level have the most prominent impact and then followed but the spatial distribution. This is related to the fact that these parameters control connectivity and hence fluid flow.

Last, a numerical experiment was developed to evaluate the ability of the proposed inversion methodology to constrain diagenesis parameters from production data. The proposed methodology was applied to a two-dimensional synthetic case. We showed that the matching of the water cut profiles made it possible to properly capture the reference diagenetic model. The optimal a parameter was pretty close to its reference value, while the spatial distribution of the heterogeneities looks like the reference one.

A next step will consist in applying the methodology described in this paper to a real carbonate field with historical production. The challenge will be to consider more data, a complex configuration of diagenetic phases and the use of the pluriGaussian algorithm.