Numerical modeling of onset and rate of sand production in perforated wells

Abstract

Shear-type failure at a wellbore or perforation is typically characterized by damage to the formation rock. For example during drilling, wellbore failure may occur with rock fragments breaking off from the wellbore wall, and for producing wells, the applied drawdown pressure can result in sanding. Perforations are more susceptible to such failures because, in general, they become less stable as the reservoir depletes. In this paper, a damage model using the Mohr–Coulomb failure criterion is formulated to better describe the failure of porous granular material. The damage variable is assumed to be related to the increase in porosity resulting from the loss of mass from the formation rock matrix. The comparisons of numerical predictions and triaxial compression tests data show that the model can accurately reproduce the mechanical behavior of sand materials. Numerical simulation of a sand production test on a perforated cylindrical specimen is performed. The proposed model demonstrated its capability to predict the accumulated sand mass and rate produced throughout the entire experiment. A threshold of equivalent plastic shear strain has been quantified to determine the onset of sand production in perforated wells; this threshold can be used for field application of sand production analysis on similar sand material. An application on a vertical well with horizontal perforations has been simulated numerically. The key objectives are to examine the critical drawdown pressure for different reservoir depletions and produced sand volume for different drawdown pressures. The critical drawdown window plot was generated and can be used to estimate the allowable drawdown pressure for different reservoir depletions. In addition, it was shown that the produced sand volume and sand mass rate increase with increase of drawdown pressure.

Introduction

Sand production is the result of transportation of failed sand grains by the flow of reservoir fluids. Sand production problems have been the focus of major discussion in the industry for a long time (Geilikman et al. 1994; Santarelli et al. 1997; Grafutko and Nikolaevskii 1998; Stavropoulou et al. 1998; Papamichos and Malmanger 2001). Operationally, the production of sand is, in general, undesirable as it can restrict productivity, lead to erosion of the completion components, impede wellbore access, and interfere with the operation of downhole equipment. Additionally, sand production requires enormous efforts at the rig to handle and dispose the large amounts of produced sands. On the other hand, sand production sometimes has the positive effect of enhancing the productivity of a well. In the production technique called cold heavy oil production with sand (CHOPS), sand production is encouraged since heavy oil is otherwise difficult to produce. This paper considers sand production as an undesirable phenomenon that must be avoided. It is therefore important to understand wellbore behavior during drilling and production/injection. Shear-type failure near the wellbore and/or perforations is typically characterized by formation-rock damage. For example during drilling, wellbore failure may occur with rock fragments breaking off from the wellbore wall and for producing wells, the applied drawdown pressure can result in sanding.

Many factors contribute to sanding, some of which are the well trajectory, orientation of perforations, degree of anisotropy between the in situ stresses, rock elastic and strength properties and drawdown. Therefore, a numerical understanding of the wellbore and perforations requires an advanced implementation of hydromechanical coupling. Such approach is essential to capture the dynamic changes of stresses and rock deformation due to pore pressure changes, temperature change, or both in the porous rock. This includes processes by which the pore pressure varies at different locations in the near-wellbore region due to non-uniform pressure profile from the formation to the well.

In the proposed hydromechanical coupling model, sand is modeled as a porous material through which the fluid filling the pores flows in accordance with Darcy’s law. Fluid flow changes the pore pressure, which in turn modifies the effective stresses, causing rock deformation and failure. An adequately robust failure criterion is required to accurately capture the redistribution of stresses and strains around the wellbore and perforations. The Mohr–Coulomb failure criterion is widely applied to the description of rock failure and rock-on-rock frictional sliding (Byerlee 1968; Al-Ajmi and Zimmerman 2006; Rutter and Glover 2012). Therefore, the sand material is modeled using a constitutive model with a Mohr–Coulomb failure criterion incorporating damage.

The mathematical formulation of the model is calibrated with laboratory test data. The comparisons between numerical predictions and triaxial compression test data are presented to demonstrate the capabilities of the proposed model to describe the mechanical behavior and failure of sands. Numerical simulation of a sand production test on a perforated cylindrical sample is also performed. The model is able to predict the amount of sand mass produced throughout the entire experiment. An application on a vertical well with horizontal perforations has been simulated numerically. The key objective is to examine the critical drawdown pressure for different reservoir depletions.

Formulation of the constitutive model

In this section, a damage model using the Mohr–Coulomb failure criterion is formulated to better model the failure of granular porous material. The incremental total strain tensor, ${\text{d}}\underline{\underline{\varepsilon }}$, is decomposed into an elastic component (reversible), ${\text{d}}\underline{\underline{\varepsilon }}^{e}$, and a plastic component (irreversible), ${\text{d}}\underline{\underline{\varepsilon }}^{p}$:

$${\text{d}}\underline{\underline{\varepsilon }} = {\text{d}}\underline{\underline{\varepsilon }}^{e} + {\text{d}}\underline{\underline{\varepsilon }}^{p}$$

(1)

Throughout the paper, the following notation and symbols will be used for tensorial calculations. A is a fourth-order tensor, $\underline{\underline{a}}$ is a second-order tensor, and $\overrightarrow {x}$ is a vector, while the symbol “:” defines an inner product of two second-order tensors $(\underline{\underline{a}}\!:\!\underline{\underline{b}}= {a_{ij}}{b_{ij}})$ or a double contraction of adjacent indices of tensors of rank two or higher [(A:a)_ij = A_ijkla_kl].

Phenomenological damage model

A phenomenological damage model to quantify the increase of porosity due to sand production is proposed. A representation of increase in porosity due to sand production is shown in a volumetric element shown in Fig. 1. At initial state in which no sand is produced, the material has an initial porosity, n₀. When hydrocarbon is produced from a sand formation, the pore pressure tends to change at the perforations and around the well. Such change in reservoir pressure may induce failure of the material leading to production of sand. The resultant increase in porosity, Δn, is related to dilatant volumetric plastic strain 〈ɛ ^p _v 〉 (Shao and Marchina 2002). The expression of porosity increase can be written as:

$$\Delta n = \left\{ {\begin{array}{*{20}l} 0 \hfill & \quad{\varepsilon_{\text{eq}}^{p} < \varepsilon_{\text{eq}}^{p0} } \hfill \\ {\int\limits_{0}^{\tau } {\left\langle {{\text{d}}\varepsilon_{v}^{p} } \right\rangle } {\text{d}}t} \hfill & \quad{\varepsilon_{\text{eq}}^{p} \ge \varepsilon_{\text{eq}}^{p0} } \hfill \\ \end{array} } \right.$$

(2)

where 〈〉 represents Macaulay brackets{〈x〉 = max (0, x)}, ɛ ^p_eq is the equivalent plastic strain, and ɛ ^p0_eq is the threshold of equivalent plastic strain corresponding to onset of sand production.

Fig. 1

Illustration of increase in porosity as a result of sand production

For sand production, the damage variable, ω, is taken as the change in porosity due to sand production. In general, the induced damage is anisotropic. However, it is assumed to be isotropic in the model for simplicity. The evolution of damage is usually determined through a damage criterion, and it is assumed to be dependent on plastic deformation only. The damage criterion is expressed as follows:

$$F_{\omega } \left( {\underline{\underline{\varepsilon }}^{p} ,\omega } \right) = \omega - \int\limits_{0}^{\tau } {\left\langle {{\text{d}}\varepsilon_{v}^{p} } \right\rangle } {\text{d}}t = 0$$

(3)

The cumulative sand volume at time t is computed from the porosity change in the damaged zone. The finite element method (FEM) is widely used in geomechanical studies (Ahmed et al. 2009). And thus, the cumulative sand volume V_sand(t) and sand mass M_sand(t) at time t are calculated from the failed elements in the FEM mesh as:

$$V_{\text{sand}} \left( t \right) = V_{\text{sand}} \left( {t - 1} \right) + \sum\limits_{i = 1}^{Ne} {\left[ {\frac{{\left\langle {{\text{d}}\varepsilon_{v}^{p} } \right\rangle }}{n}} \right]_{i,t} } \varOmega_{i}$$

(4)

$$M_{\text{sand}} \left( t \right) = V_{\text{sand}} \left( t \right) \cdot \rho$$

(5)

where Ne is the number of elements, V_sand(t) and V_sand(t − 1) are the cumulative volume of sand produced at time t and t − 1, respectively, n is the porosity, and dɛ ^p _v is the incremental plastic strain of an element between t and t − 1. Ω_i is the volume of an element. M_sand(t) is the cumulative sand mass produced at time t. ρ is the density of sand.

Elastoplastic damage model

It is postulated that a thermodynamic potential exists for damaged material which is the sum of the energy from elastic strain and the locked energy from plastic hardening:

$$W\left( {\underline{\underline{\varepsilon }}^{e} ,\gamma^{p} ,\omega } \right) = \frac{1}{2}\left[ {k\left( \omega \right)\left( {\varepsilon_{v}^{e} } \right)^{2} + 2\mu \left( \omega \right)\underline{\underline{e}}^{e} :\underline{\underline{e}}^{e} } \right] + W^{p} \left( {\gamma^{p} ,\omega } \right)$$

(6)

ɛ ^e _v is the elastic volumetric strain, $\underline{\underline{e}}^e$ is the elastic deviatoric strain tensor, γ^p is the generalized plastic shear strain, and W^p(γ^p, ω) is the locked energy from plastic hardening. The general constitutive equation is obtained by the standard derivation of the thermodynamic potential with respect to elastic strain:

$$\underline{\underline{\sigma }} = \frac{{\partial W\left( {\underline{\underline{\varepsilon }}^{e} ,\gamma^{p} ,\omega } \right)}}{{\partial \underline{\underline{\varepsilon }}^{e} }} = k\left( \omega \right)tr\left( {\varepsilon_{v}^{e} } \right)\underline{\underline{\delta }} + 2\mu \left( \omega \right)\underline{\underline{e}}^{e}$$

(7)

The proposed elastoplastic damage model considers the elastic moduli are affected by damage. The elastic behavior is characterized by the bulk modulus, k(ω), and the shear modulus, μ(ω). These two moduli are degraded by the induced damage (Nemat-Nasser and Hori 1993; Krajcinovic 1996; Pensee 2002) due to sand production and expressed as:

$$k\left( \omega \right) = k_{0} \left( {1 - \omega } \right),\quad \mu \left( \omega \right) = \mu_{0} \left( {1 - \omega } \right)$$

(8)

k₀ and μ₀ are the initial bulk and shear moduli, respectively given by:

$$k_{0} = \frac{{E_{0} }}{{3\left( {1 - 2\nu_{0} } \right)}},\quad \mu_{0} = \frac{{2E_{0} }}{{1 + \nu_{0} }}$$

(9)

where E₀ and ν₀ are the Young’s modulus and Poisson’s ratio of undamaged material, respectively.

The plastic deformation of the sand material is described by a plastic yield surface, plastic potential, a hardening law and a failure surface. The Mohr–Coulomb failure criterion (Coulomb 1776) is widely used to describe the behavior of sand material, and it is adopted in this paper in the following invariant form:

$$F = p^{\prime}\sin \phi_{\text{f}} + J\left( {\cos \theta - \frac{{\sin \theta \sin \phi_{\text{f}} }}{\sqrt 3 }} \right) - C_{\text{f}} \cos \phi_{\text{f}} = 0$$

(10)

C_f and ϕ_f are the cohesion and friction angle at failure state, respectively. p′ and J are the effective mean stress and deviatoric stress, respectively, defined by:

$$p' = \frac{1}{3}tr\left( {\underline{\underline{\sigma }} '} \right),J = \frac{{\sqrt {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } }}{\sqrt 6 },\;{\text{and}}\quad \theta = \frac{1}{3}\arcsin \left( {\frac{{ - 3\sqrt 3 J_{3} }}{{2J_{2}^{3/2} }}} \right)$$

(11)

The variable θ represents Lode’s angle, and the Lode’s function describes the variation of yield stress with loading direction in the deviatoric plane.

The plastic yield surface is defined as

$$f_{p} = p'\sin \phi_{{_{p} }}^{\omega } + J\left( {\cos \theta - \frac{{\sin \theta \sin \phi_{{_{p} }}^{\omega } }}{\sqrt 3 }} \right) - C_{p} \cos \phi_{{_{p} }}^{\omega } = 0$$

(12)

The classical Mohr–Coulomb failure criterion assumes a linear hardening law in which cohesion changes from an initial value at yield point into a final value at failure state. In addition, friction angle is taken as constant. However, laboratory evidence showed that cohesion and friction angle evolve nonlinearly in the hardening phase, wherein the values of cohesion and friction angle (C,ϕ) vary from (C₀,ϕ₀) at the initial yield state to (C_f,ϕ_f) when the failure surface is reached: f_p → F. The hardening laws are written as follows:

$$C_{\text{p}} = C_{0} + \left( {C_{\text{f}} - C_{0} } \right)\frac{{\gamma^{p} }}{{H_{1} E + \gamma^{p} }}$$

(13)

$$\tan \left( {\phi_{p} } \right) = \tan (\phi_{0} ) + \left( {\tan (\phi_{f} ) - \tan (\phi_{0} )} \right)\frac{{\gamma^{p} }}{{H_{2} E + \gamma^{p} }}$$

(14)

H₁ and H₂ are two parameters that control the kinetics of hardening. Figure 2 shows the yield and failure surfaces in the stress plane. To account for the influence of material damage due to sand production in the strain softening phase, the cohesion and friction angle are degraded by introducing the damage effect (Mohamad-Hussein and Shao 2007a, b), as follows:

$$C_{\text{p}}^{\omega } = \left( {1 - \omega } \right)C_{\text{p}}$$

(15)

$$\tan (\phi_{{_{p} }}^{\omega } ) = \left( {1 - \omega } \right)\tan (\phi_{p} )$$

(16)

Fig. 2

Illustration of the yield and failure surfaces in the stress plane

Triaxial tests carried out on sand materials show plastic volume dilation caused by the imposed deviatoric stress. In this paper, sand production is related to plastic dilation, and thus, it is necessary to correctly describe the transition from plastic compressibility to plastic dilation by the use of a non-associated flow rule. The plastic flow rule is controlled by the plastic potential and expressed by

$$Q = p^{\prime}\sin \psi_{{_{p} }}^{\omega } + J\left( {\cos \theta - \frac{{\sin \theta \sin \psi_{{_{p} }}^{\omega } }}{\sqrt 3 }} \right) - C_{\text{p}}^{\omega } \cos \psi_{\text{p}}^{\omega } = 0$$

(17)

$\psi_{\text{p}}^{\omega }$ is the dilation angle which describes the transition between plastic compressibility and the plastic dilatancy.

The plastic strain increment is calculated from the following expression:

$${\text{d}}\underline{\underline{\varepsilon }}^{p} = {\text{d}}\lambda \frac{{\partial Q\left( {\underline{\underline{\sigma '}} ,\omega } \right)}}{{\partial \underline{\underline{\sigma '}} }}$$

(18)

dλ is the plastic multiplier that can be determined from the consistency condition.

The constitutive model has been implemented in VISAGE finite element code.

Workflow for sand production prediction

Figure 3 shows the sand production prediction workflow. The workflow is divided into three main stages:

Fig. 3

Workflow for sand production prediction

• Sand formation condition prior to production. The sand formation has the initial mechanical properties, initial pore pressure and preproduction stress.

• Drawdown pressure application. A drawdown pressure is applied at the wellbore or perforation wall. Due to the applied drawdown pressure, the pore pressure will change around the wellbore and perforations resulting in changes of the in situ stresses and strains. At this stage, the poro-elastic stresses and strains are computed using the finite element method.

• Sand production analysis. Sand failure is checked, and if the changes in effective stresses are sufficiently high such that the failure criterion is violated, the stresses are then redistributed accounting for plasticity. The damage variable “porosity change” is computed from the dilatant plastic volumetric strain, and the sand production rate and volume are calculated. The sand production mechanism induces degradation of elastic and strength properties.

Axial response

To illustrate the performance of the elastoplastic damage model under uniaxial loading conditions, the axial response was investigated for uniaxial compression and extension tests, as shown in Fig. 4. The numerical response of the uniaxial extension test shows a linear elastic region that is followed by a sharp deterioration of the strength due to induced damage. The degradation of the elastic properties resulted in softening behavior. On the other hand, the uniaxial compression test showed three main regimes. The material behaved elastically until initial yield is reached. Plastic hardening occurred thereafter followed by rock dilation. The final regime is post-peak softening behavior, which resulted from the evolution of damage and deterioration of the material properties. Note that when the material is fully damaged where the damage scaler variable is equal to 1, the residual stress declines to zero.

Fig. 4

Uniaxial compression and extension test response

Calibration of the model and numerical simulations

In this section, numerical simulations of triaxial tests are presented for Vosges sandstone (Khazraei 1995) and oil-bearing sand (Kosar 1989). The main objective is to evaluate the capabilities of the damage model to predict the mechanical behavior of sand materials. The parameters used in the numerical simulations were determined from conventional triaxial compression tests.

The initial elastic parameters (Young’s modulus and Poisson’s ratio) are identified from the linear section of the stress–strain curve in a triaxial compression test. Figure 5 illustrates the linear section and the initial Young’s modulus on the stress–strain curve. The initial elastic parameters are therefore determined as:

$$E = \frac{\Delta q}{{\Delta \varepsilon_{\text{axial}} }}$$

(19)

$$\nu = - \frac{{\Delta \varepsilon_{\text{radial}} }}{{\Delta \varepsilon_{\text{axial}} }}$$

(20)

where q is the deviatoric stress, ɛ_axial is the axial strain, and ɛ_radial is the radial strain.

Fig. 5

Illustration of the linear elastic region and initial Young’s modulus—data from Kosar (1989)

Figure 6 shows the yield and failure surfaces. The initial cohesion (C₀) and the failure cohesion (C_f) are determined from the intersection of the yield and failure surface with the shear stress axis, respectively. On the other hand, the initial friction angle (ϕ₀) and the failure friction angle (ϕ_f) are computed from the slope of the yield and failure surfaces, respectively.

Fig. 6

Yield and failure surfaces—data from Kosar (1989)

For the determination of the hardening parameters H₁ and H₂, the cohesion and coefficient of friction are calculated for selected points on stress strain curves in the triaxial compression tests. Then, hyperbolic lines are plotted to fit the experimental points to obtain representative values for H₁ and H₂. The evolution of both cohesion and coefficient of friction with plastic shear strain, within the hardening phase, are shown in Fig. 7, which illustrates the hyperbolic shape of the evolution.

Fig. 7

Evolution of cohesion (left) and coefficient of friction (right) with plastic shear strain within the hardening phase—data from Kosar (1989)

The model parameters are summarized in Table 1. Figures 8 and 9 show the comparison between experimental data and numerical simulations for triaxial compression tests with different confining pressures for Vosges sandstone and oil-bearing sand, respectively. There is a reasonable to good agreement between the experimental data and numerical simulations results for the entire range of confining pressure. The model is able to predict the main features of the sands behavior, such as hardening and failure.

Table 1 Damage model parameters for Vosges sandstone and oil-bearing sand

Fig. 8

Comparison of numerical simulations and experimental data of triaxial compression tests with confining pressures of 5, 20, and 40 MPa (Vosges sandstone)

Fig. 9

Comparison of numerical simulations and experimental data of triaxial compression tests with confining pressures of 50, 150, 250, and 450 kPa (oil-bearing sand)

Numerical simulation of sand production test

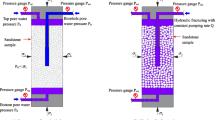
A sand production experiment, reported by Rahmati et al. (2012), has been performed to examine the onset and growth of sand production from a perforated cavity. A cylindrical sample 10 inches high and 6 inches in diameter has been selected for the experiment. A perforation of 0.5 inch diameter and 2 inches length is drilled centrally at the base of the sample. The sample is placed in the test equipment as illustrated in Fig. 10. During the test, the sample is subjected to hydrostatic stress applied at the external surfaces. Fluid is injected from the top of the sample and flow through the perforation. Sand solids are collected and monitored throughout the experiment, which lasted approximately 1300 min. Figure 11 shows the recorded confining pressure, injection rate, and sand mass produced during the experiment. The experiment shows that onset of sand production occurred at a pressure of approximately 5250 psi and a flow rate of approximately 20.7 in³/min. Such data are highly useful to understand the sand production behavior. By simulating such experiment, a threshold of equivalent plastic shear strain can be obtained and applied for onset of sand production.

Fig. 10

Sand production testing equipment

Fig. 11

Sand production test data

A finite element model has been built to simulate the experiment. The combined hydraulic (fluid flow) and mechanical (stress change) processes have been considered by performing fully coupled single-phase fluid flow simulation. Due to the symmetrical geometry, the simulation has been performed on a 2D axisymmetric model. Figure 12 illustrates the geometric domain and the boundary conditions that have been considered for the numerical analysis.

Fig. 12

Geometric domain and boundary conditions of numerical model

Figure 13 shows the evolution of simulated damage at the perforation wall. It is clear that damage increased due to the increase in rock dilation. However, there exists a significant sudden increase in the dilation beyond point 2. This is mainly related to the post-failure behavior and occurrence of strain localization around the perforation wall. The corresponding “deviatoric stress versus maximum principal strain” behavior curve is illustrated in Fig. 14. Point 1 represents the onset of damage point, the zones 1–2 are the plastic hardening zone, and the softening zone is shown in zones 2–3–4.

Fig. 13

Evolution of scalar damage variable at the perforation wall

Fig. 14

Deviatoric stress versus maximum principal stress behavior at the perforation tip

Figure 15 presents the distribution of damage at the end of the experiment. A damage zone occurred around the perforation wall due to sand production. The damage variable is directly related to rock dilation. Therefore, the volume and mass of sand produced can be calculated directly throughout the experiment. Figures 16 and 17 present the comparison between the numerical simulation and experimental data with respect to accumulated produced sand mass and sand mass rate, respectively. There is reasonable to good agreement between the numerical prediction results and the experimental data. This illustrates that the model is able to predict reliably the amount and rate of produced sand at different times.

Fig. 15

Distribution of damage along the perforation wall at the end of the experiment

Fig. 16

Comparison between numerical simulation results and experimental data on accumulated produced sand mass

Fig. 17

Comparison between numerical simulation results and experimental data on produced sand mass rate

The onset of sand production condition has been examined to quantify the threshold of equivalent plastic shear strain. The profile of equivalent plastic shear strain has been plotted along the perforation wall at onset of sand production (Fig. 18). It is clear that the plastic strains occurred along the perforation wall has the highest value near the tip. This profile was used to determine the threshold of equivalent plastic shear strain, ɛ ^p0_eq , to be approximately 2.66%. This threshold value can be used as an indicator for onset of sand production in field applications of similar sand material. For example, for a perforated well, an equivalent plastic shear strain exceeding 2.66% indicates potential sanding in the well.

Fig. 18

Equivalent plastic shear strain profile along the perforation at onset of sand production

Production from perforated well

The validation of the constitutive model has been successfully carried out in “Axial response” and “Calibration of the model and numerical simulations” sections with laboratory test data. In this section, modeling of production from a perforated well is presented. The key objectives are to quantify the critical drawdown pressure for different reservoir pressures and produced sand volume for different drawdown pressures. A vertical well of diameter 0.30 m was assumed. Four 90° apart perforations were considered, each of 0.50 m length. The geometrical domain of the wellbore and perforation is shown in Fig. 19. The main phases adopted in the numerical modeling are:

Fig. 19

Geometrical domain of wellbore and perforations

• Creation of the 3D near wellbore model. The construction of the near wellbore model involved creation of a high-resolution grid around the wellbore and perforations to capture detailed stress redistribution (Fig. 20).

  Fig. 20

  

  Grid distribution around wellbore (left) and perforations (right)

• Predrill stress analysis. In this analysis, the preproduction initial stresses and pore pressure are imposed on the grid.

• Wellbore and perforations excavation. In this step, the materials inside the wellbore and perforations are removed and an internal load is applied to represent the bottom hole pressure. In this phase, the bottom hole pressure is considered to be equal to the pore pressure. Figure 21 shows the excavation process technique.

  Fig. 21

  

  Excavation process technique

• Production modeling. In production modeling, the production is simulated by applying drawdown pressure at the wellbore wall.

The predrill initial stresses and initial pore pressure are

$$\left\{ {\begin{array}{*{20}l} {\sigma_{v}^{00} = 3275\,{\text{psi}}} \hfill \\ {\sigma_{H\hbox{max} }^{00} = 0.99\sigma_{v}^{00} } \hfill \\ {\sigma_{h\hbox{min} }^{00} = 0.92\sigma_{v}^{00} } \hfill \\ {P^{00} = 2000\,{\text{psi}}} \hfill \\ \end{array} } \right.$$

(21)

The focus of this example is to evaluate the sanding tendency due to production. Therefore, the production phase has been evaluated at three reservoir pressures (2000, 1875 and 1750 psi) and four drawdown pressures (DDP) of 100, 250, 375 and 500 psi. For a specific reservoir pressure, a drawdown pressure is applied at the perforation walls. Due to the applied drawdown pressure, the pressure tends to diffuse around the perforations and the wellbore. The pore pressure distribution has been simulated using a single-phase model. Figure 22 shows the distribution of pore pressure change due to drawdown pressure of 500 psi. In addition, the profile of pore pressure change from the perforation wall is illustrated in Fig. 23. The pore pressure change induces changes in effective stresses, and if the effective stress changes are significant, they may result in rock damage and lead to sand production.

Fig. 22

Distribution of pore pressure change (psi): 3D view (left); top view (middle); vertical cross-section (right)

Fig. 23

Pore pressure change (psi) profile from perforation wall for a drawdown pressure of 500 psi

Figure 24 presents the distribution of rock damage around the wellbore due to production. As expected, the perforations aligned along the maximum horizontal stress direction (angle = 0° and 180°) have higher damage compared to the perforations aligned along the minimum horizontal stress direction (angle = 90° and 270°). The maximum equivalent plastic shear strain for different reservoir pressures versus drawdown pressure is shown in Fig. 25. The red dotted line represents the threshold (2.66%) for onset of sand production based on the sand production test. These curves show that the maximum equivalent plastic shear strain increases with reservoir depletion and with increase in drawdown pressure. The safe drawdown changes with depletion were also evaluated, and Table 2 summarizes the critical drawdown pressure corresponding to onset of sand production for different reservoir pressures.

Fig. 24

Distribution of rock damage at the entrance of perforations around the wellbore due to production

Fig. 25

Maximum equivalent plastic shear strain for different reservoir pressures versus drawdown pressure

Table 2 Critical drawdown pressure corresponding to onset of sand production for different reservoir pressures

The diagram in Fig. 26 shows a “safe drawdown window” which shows the predicted safe drawdown for particular combinations of completion, rock strength, and initial reservoir pressure and stress conditions. The plot of bottom hole flowing pressure versus reservoir pressure is divided into three zones:

Fig. 26

Safe drawdown window plot at a single depth

• Zone of no production above the diagonal line where bottom hole flowing pressure is higher than reservoir pressure.

• Zone of well production (bottom hole flowing pressure is below reservoir pressure) which is subdivided by the predicted safe drawdown line into:

• Zone of sand-free production (green zone) and.

• Zone of sand (plus oil) production (red zone).

With the increase in depletion, the amount of drawdown that can be applied to the completion without failing the rock changes, and one of the key goals of sand production prediction is to predict this safe drawdown line in the safe drawdown window.

For onset of sand production, stress re-distribution around the wellbore/perforation is of main interest. Figure 27 shows typical sand representation at a point on the wellbore/perforation wall. Critical drawdown window plot has been generated from numerical analysis as shown in Fig. 28. A zoom-in of the critical drawdown window plot is shown in Fig. 29.

Fig. 27

Inclined wellbore with perforation tunnel

Fig. 28

Safe drawdown line plot from numerical analysis

Fig. 29

A zoom-in of critical drawdown window plot from numerical analysis

In addition to the onset of sand production, the produced sand volume is determined. Figures 30 and 31 show the sand volume produced and sand mass rate for different drawdown pressures, respectively. The curves show that the produced sand volume and sand mass rate increase with increase in drawdown pressure.

Fig. 30

Produced sand volume at reservoir pressure of 1750 psi for different drawdown pressures

Fig. 31

Produced sand mass rate at reservoir pressure of 1750 psi for different drawdown pressures

Conclusions

A damage model using the Mohr–Coulomb failure criterion has been formulated to better describe the failure of porous granular material. The damage variable is assumed to be related to the increase in porosity resulting from the loss of mass from formation rock matrix. The performance of the constitutive model has been validated against Vosges sandstone and oil-bearing sand materials test data. Simulations of triaxial compression tests at different confining pressures have been performed and compared with the laboratory test data. The showed that the model is able to reliably reproduce the mechanical behavior of the sand materials.

Simulation of sand production tests has been carried out on a perforated sample. The model was able to predict the amount of sand mass produced with time during mechanical loading and fluid flow inside the sample. A threshold of equivalent plastic shear strain of approximately 2.66% which represents the onset for sand production has been computed.

Numerical analysis of a perforated well has also been conducted. The key focus of the analysis is to evaluate and examine the critical drawdown pressure for different reservoir pressures. The results showed that the equivalent plastic shear strain increased with reservoir depletion and an increase in drawdown pressure. Further evaluations were conducted on safe drawdown changes with depletions. The critical drawdown window plot was generated and can be used to estimate the allowable drawdown pressure for different reservoir depletions. In addition, it was shown that the produced sand volume and sand mass rate increase with an increase in drawdown pressure.